从“开篇、连线、勾廓”的视角谈章首课设计——以苏教版“5.1二次函数”为例

江苏省无锡市张泾中学 万志建

每一章教学内容的第1课时，或者每一章引言加上第1课时，简称章首课，近年来，成为研究的热点.较为流行的观点是，章首课要在系统思维与整体观念的引领下对整章内容做一个提纲挈领的“预览”，使学生在后继具体内容学习之前先有一个全局的认识.但很多课例中，有些教师就课论题，内容不够，题目来凑，往往把课上得繁、难、偏，学生兴味索然；有些教师为求整体效果，把章首课上成全章内容的介绍课、流水课，对第一节的知识要点、核心概念却一带而过，以致很多听课教师感叹这种章首课有些“假、大、空”，学生看似学了很多，但究竟懂了多少，不得而知.

下面以苏科版“5.1二次函数”为例，谈如何从“开篇、连线、勾廓”的视角谈章首课的设计.

一、开篇：溯源设境，开宗明义

所谓“开篇”，指设计每一个单元整体教学的章首课导入时，要从宏观的角度分析本章知识的缘起，是为解决生活中实际问题需要还是源于数学前后章节发展完善的需要，而后者由于数学知识具有一定的系统性与完整性，更容易找到前后的关联，在此基础上，结合学生已有的生活现实和数学现实，找到学生熟悉的生活情境或与新知关联性较强的章节，作为铺垫参考，让学生在情境的展现过程中，由此及彼点燃思维，激活基本活动经验，联想数学思想方法，明确学习目标，明晰学习内容.

片段1：由形引数，初步感悟

教师出示投篮、喷泉、跳长绳的图片：从中可抽象出什么图形？有哪些特征？请画出这些图形.

生1：发现一些弯曲的弧线，它们先升后降或先降后升，呈对称分布.

师：不错，这条曲线是一次函数图像吗？是反比例函数图像吗？

生：（齐）不是！

师：初中阶段数学内容的编排，环环紧扣，螺旋上升，回顾函数的学习，我们先学了一次函数y=kx+b(k≠0)，特殊地，若假设y=0，则可得到一元一次方程kx+b=0（k≠0），也就是说，一元一次方程与一次函数是从特殊到一般的关系.后来我们又学了一元二次方程ax2+bx+c=0（k≠0），相应的又会是什么走向呢？

生：（齐）会学习二次函数！

师：对！这就是我们今天要学习的二次函数，它的图像形如物体抛出时形成的轨迹，我们形象地称它为“抛物线”.

设计说明：二次函数的引入，既可从具体的图形较为直观地引入，激趣引探，由形想数；也可从函数的发展，由一次函数到二次函数提升完善的需要引入，让学生领会教材的编排设计意图，感受其中关联，为后继学习埋下伏笔.基于此，本课双管齐下，先从直观的图形出发，由形象到抽象，让学生初观其形，再画形知形，由形猜数，层层深入，让学生对本章的内容有一个大概的方向和思路.

二、连线：双线并进，夯实概念

所谓“连线”，指基于章引言“开篇”这个宏观导入之后，回归到本课的知识要点（一般章首课往往从概念教学开始），从中观和微观层面，布点连线，通过剖析知识“从哪里来？是什么？怎样学？怎样用？向哪里去”串联起一条教学活动（问题）主线，对多个知识点还要找到它们的相互关联，形成知识链.除了要抓住显性知识这条明线，更要抓住本课的知识素材所隐含的数学思想方法暗线，以及在解决问题过程中所用到的思想方法，促进学生高阶认知能力的形成，这也是确保课堂知识要点剖析到位，落地生根，避免章首课“假、大、空”的有效方法.

片段2：一题散花，落红归根

师：数学源于生活，请看例1：一张长为6、宽为4的矩形硬纸片，四周剪去一个边长为x的小正方形，把它围成一个无盖的长方体纸盒，请举一个跟面积（用y表示）有关的问题.

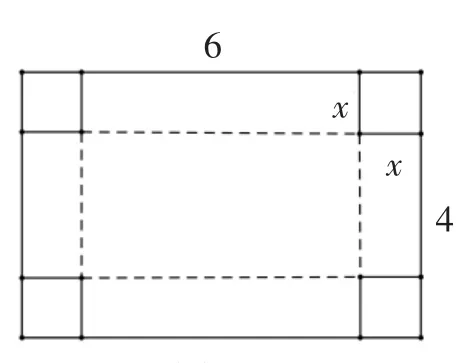
图1

生1：剪去的每个小正方形的面积y=x2.

生2：长方体的表面积y=-4x2+24.

生3：长方体的侧面积y=-8x2+20x.

生4：长方体纸盒的底面积为y=4x2-20x+24.

师：这些函数中，自变量是什么？有什么共同特征？

生5：自变量是x，且最高次数为2.

师：这些函数表达式中，哪个最帅、最威武？请结合它的相貌，描述二次函数的定义.

生6：最后一个最帅，结合一元二次方程的一般式，可把形如y=ax2+bx+c（a≠0）的函数叫作二次函数，其中x是自变量，y是x的函数.

师：说得很到位！定义中的关键词是什么？

生7：“（a≠0）”及自变量最高次是“二次”.

设计说明：数学情境的设计，尽可能围绕某一情节串联起来，呈现生活、简约、发散、高效的意境，产生“少而精”“简而丰”的教学效果.对于核心概念的形成，从模糊到清晰，从具体到抽象，从发散到聚集，层层推进，指向本质.

片段3：紧扣概念，深度学习

教师出示例2.

生活中的数学：清明节，老师到离家7.2km的鱼塘垂钓，请根据以下情境设计问题，得到函数关系式，说出自变量的取值范围，并判断是否为二次函数.

（1）老师到鱼塘所需的时间为t，平均车速为v，问：____________？

（2）鱼儿跃出水面时，平静的水面被激起层层波纹，不断向外扩展，设扩大的圆的半径为r，问：_______________？

（3）在鱼塘旁的空地上，主人想用篱笆围成长方形的围栏饲养小鸭，若篱笆长为16米，设___________，问：_____________？如果在围栏内铺设地砖，每平方米10元，其他费用为100元，那么________________？

生答略.

例3请结合用一元二次方程解决实际问题的经历，举一些二次函数的例子.

生答略.

例4若y=3x|m|+x-3为二次函数，求m的值.

生8：当m=±2时，y=3x|m|+x-3为二次函数.

师：很好！二次函数强调自变量的最高次项是二次项且系数不为0，请在上题的基础上综合这二者设计问题.

生9：当m为何值时，函数y=（m+2）x|m|+x-3是二次函数？

师：不错，二者兼顾！

教学说明：概念的教学设计应考虑概念的来源是什么，内涵是什么，与之相关的概念相互之间的关联是什么，等等.例2与例3分别体现了函数源于生活又回归生活，加深理解概念的同时，培养学生多种能力；最后一题则是让学生围绕概念要点自主设计问题，更有利于学生掌握知识的本质，促进对概念的深度理解.

片段4：由数想形，呼应课首

师：根据函数的学习经验，接下来我们应该学习？

生：（齐）二次函数的图像.

师：很聪明，在上述函数式中，你会先挑哪一个作图？为什么？

生10：会先挑y=x2下手，因为这个式子最简洁！

师：从特殊到一般，很好，请根据函数y=x2的表达式的特征，说说它的图像具有哪些特征.

学生通过特殊数值的尝试，得出函数y=x2的性质.（略）

师：课后请同学们结合这些特征去试一试作图，下节课我们将具体讲解！

教学说明：课虽止，思未止，一节数学课的结束，并不意味着教学内容和学生思维戛然而止，而应“收”中有“展”，既要及时回顾总结，使前后知识成为一个完整的体系，还要让学生对后继的知识有一个初步的认识，即学了这节课内容之后，接下来要解决什么问题，最好有一个暗示或伏笔，让学生心生向往，让兴趣和思维得到积极、有效的延伸.

三、勾廓：类比联想，成竹在胸

所谓“勾廓”，指章首课在教学安排中，要留有一定的时间引导学生探寻本章知识的发展规律或与已学过的知识间的相互关联、“共性通法”，激活学生相似的学习经验，从宏观的角度勾画全章的轮廓，即知识框架及学习方法，获得基础性、概貌性的认识及掌握基本的学习方法，让学生在未学之前，已成竹在胸，心驰神往，这也是章首课的特殊性所在.

片段5：类比迁移，建构框架

师：请结合一次函数的学习经验，猜想二次函数会介绍哪些内容，以及怎样学这些内容.

学生通过小组讨论得出如下知识结构图及学习方法：

主要是通过类比、从特殊到一般及数形结合的方法学习二次函数.

教学说明：章首课，除了要让学生理解核心概念，还要引导学生通过类比同类章节间的相互关联或研究知识的发展走向，掌握这一章节的基本结构，以及研究这一章节的基本态度或方法.

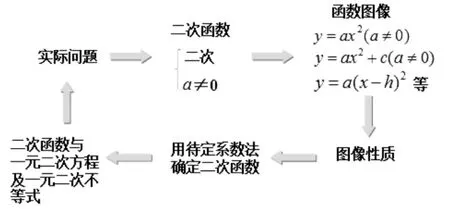
图2

写在最后：初中阶段的章首课，大多是第1课时加章引言，相对内容较多，安排紧凑，既要让学生掌握本课时的重点、难点，又要兼顾建构本章的知识体系，让学生对章节内容及结构形成概貌性的认识，在清晰的目标指引下进行后续学习.因此在章首课中，要合理分配时间.首先，要确保学生对本课的知识要点、核心概念达到理解、掌握，这也是本课教学的重心所在.其次，指导学生完成对全章内容的推演，时间段可安排在课首或课尾；内容上宜粗不宜细，宜宏观不宜微观；方法上可根据章节知识的自身发展规律或同类章节间的相互关联，预知本章知识体系，初通学习方法，激发学习期望.