精选“形异质同”问题，促进学生想深想透——由两道习题讲评的教学片段说起

江苏省扬州市高邮城北中学 朱爱华

当前的数学课堂教学生态下，大量的课都在讲习题，然而很多教辅资料上的习题量大、质劣，如果不加取舍、有的放矢进行选练和讲评，则学生常常难以走出题海.特别是对于一些习题的讲评，如果教师本人对“形异质同”问题缺少足够的“眼力”将其识别出来，并引导学生进行对比、分析、内化，这种解题或解题教学常常会入宝山而空返，不利于学生学会解题、学会洞察问题深层结构.本文从近期习题课上搜集到的两道“形异质同”习题出发，记录学生的解法及我们对其的讲评与回顾反思，希望能加深大家对“形异质同”习题在解题教学过程中的价值的认识.

一、两道“形异质同”习题的教学片段分享

说明：以下是关于题1、题2的教学讲评记录，这两道习题散见在一份单元检测试卷中，从阅卷情况来看，学生完成得都不太好，所以我们对这两道“形异质同”习题进行关联式讲评.

题1：若a＋b=-2，且a≥2b，则以下说法正确的是（ ）.

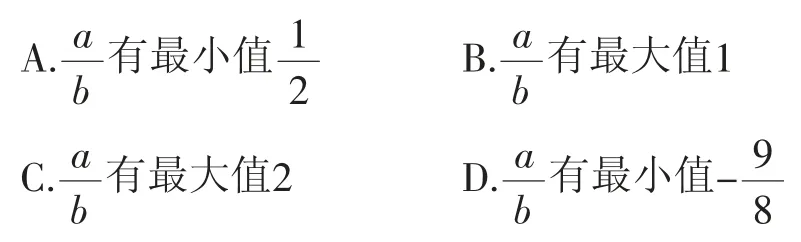
生1：依次分不同情况讨论.情形1：a＞0，b＞0，结合a＋b=-2，可得不符合题意，舍去；情形2：a＜0，b＜0；情形3：a＞0，b＜0；情形4：a＜0，b＞0，结合a≥2b，可得不符合题意，舍去.则b＜0.又a≥2b，则

生2：与生1相比，判断b＜0的思路不同.由a＋b=-2，得a=-2-b.又a≥2b，则-2-b≥2b，则b≤，即b＜0.后续思路一致.

生3：用特殊值法与排除法，获得答案.比如，先类似生2的方法，解得，接着选定特殊值：当，排除B；当a=1、b=时，，排除A、D.于是，获得答案.

简评：生1思路清楚，首先判断a或b的正负，与生2不同的是进行了分情况讨论.相比较而言，生2的判断方法更好，用消元的思想求未知数的取值范围，更精准.而生3则用了选择题的技巧性解法——排除法，当然这种解法的“力量感”“弱”了很多.生4出现了两处错误.错误之一：分析出b有最大值，而根据不等关系，a应当有最小值.错误之二：将看作a×，b越大，但在范围b≤内会越来越小，因此的最大值是2这个说法有误.

教师解法：针对A、B、D选项，可以借助双曲线的位置来“数形结合”地分析.比如，先“消参”得到，再根据图像，以及，可以看出的最大值是2，最小值不存在.

题2：已知三个非负实数x、y、z满足则代数式x＋4y＋3z的最小值为？

学生解法：用加减消元法消参，得由x≥0，y≥0，得解得10≤z≤20.进一步将待求的代数式“化简”，得到x＋4y＋3z=150-4z.要使结果最小，则4z最大.当z=20时，x+4y+3z取得最小值70.

教学记录：在评讲过程中，题目中有几个等量关系和不等关系，常用思路是利用等式消元，利用不等式求范围.与“题1”稍有不同的是未知数的个数不同.当出现三个未知数但只有两个方程时，一般考虑整体思想或者“消参”，即用一个未知数表示另外两个未知数.

二、关于“形异质同”题的教学思考

1.备课要善于将“形异质同”题归类呈现

当前在集体备课时，备课组内很多功夫都花在选题上，把好例、习题的质量关，这是有效的.特别是现在有些组题网站功能强大，只要设定选题范围（按某种版本教材的章节）再加上一些关键词进行选题，很快就能生成大量形式上高度相同的问题.但是，我们的教研备课不能止步于此，还需要考虑选用的例、习题之间的联系，而不只是把一些“形同质同”的题拼凑在一起，还需要考虑与一些“形异质同”问题进行关联，组合在一起以“问题串”或题组归类的形式呈现，让学生能通过对这些题组的练习，感悟问题的深层结构，使得以后碰到类似结构问题时，能够识别、迅速转化.当然，这就要求教师在备课时下足功夫，教师本人首先要有识别“形异质同”问题的眼力.

2.教学时可安排学生上台展示解法或思路

当体现同类结构的题组呈现之后，可以先安排学生独立思考，然后在小组内适当交流，再全班汇报展示.教师针对学生可能的解法要有充分的预设，这样可以从容、灵活地驾驭课堂，做出恰时恰点的诊评，跟进必要的追问，使学生的解法或对问题的理解全面而深刻，而不只是获得问题的答案.比如，上文中的题例解决之后，可进行适当小结，让学生认识到对于这类“多参数”问题，成功求解需要“消参”，将多元方程或不等式转化为一元一次方程或二元一次方程组来思考，并最终向一元一次不等式转化，实现思路贯通.

3.引导学生开展解题后的必要回顾与反思

在一些较难习题归类讲评之后，还要进行必要回顾与小结，让学生“回看”探究与求解过程，提炼出问题结构，积累基本图形及性质.除了上文提供的这类涉及“消参”的问题，七年级学生在初学平面几何时，还有很多几何基本图形及性质需要通过解后回顾和反思进行提炼和深化.比如，三角形的两条内角平分线夹角问题、一条内角与一条外角平分线夹角问题、两条外角平分线夹角问题，如果分开练习讲评，则是入宝山而空返，学生学到的往往是零散的数学内容，需要将它们集中在一节课中进行讲评、对比，最后阶段还要把它们集中到一个图形中让学生看清它们之间的关系.再比如，初学三角形的角时，学生常常遇到以下一类问题：

题组：如图1，在△ABC中，AE、AD分别是△ABC的角平分线、高线.

（1）∠B=40°，∠C=70°，求∠DAE的度数；

（2）∠BAC=70°，∠BAC=70°，求∠DAE的度数；

（3）∠C-∠B=30°，求∠DAE的度数；

（4）请猜想∠DAE与∠B和∠C之间有怎样的数量关系，并说明理由.

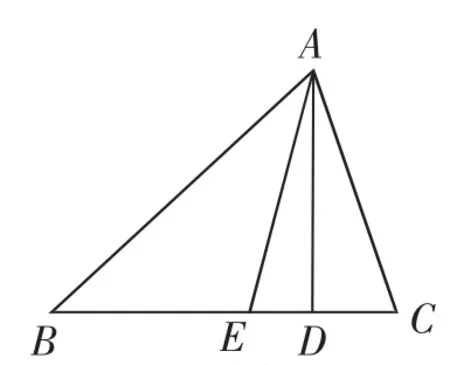
图1

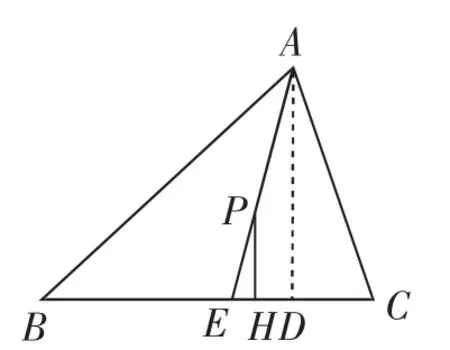
图2

教学组织：学生练习这组问题之后要提炼出从三角形同一顶点引出的角平分线与高线的夹角等于三角形另外两角差的绝对值的一半，并且让学生感受到这组“问题串”是从特殊走向一般的设问方式，属于“并列式问题”，但需要“递进式”求解.如果只是满足于上述题组的训练，还不够深入，讲评之后，我们还可继续跟进如图2、图3这样的变式问题，在图2中，在线段AE上取点P，作PH⊥BC于点D，分析∠EPH与∠B和∠C之间有怎样的数量关系；进一步，点P在线段AE的延长线上时，作PH⊥BC于点D，分析∠EPH与∠B和∠C之间有怎样的数量关系，并且引导学生作出辅助线“高AD”来实现问题快速转化.

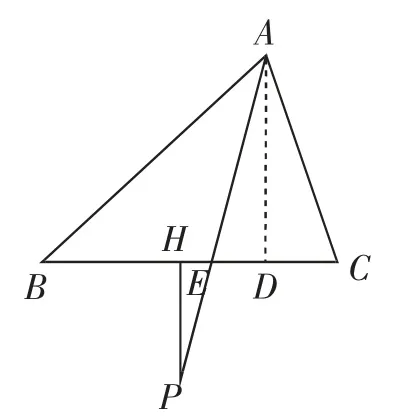
图3

三、写在后面

近读郑毓信教授著作，郑教授反复强调广大一线教师要有思辨力、要有定力，于很多创造名词或概念的教学方法与教学模式的研究而言，我们如何才能成为真正的主体而不是永远处于“被运动”的地位？郑教授建议：“立足专业成长，关注基本问题.”在这个角度上看，我们应该从自己的日常教学工作出发，搜集、整理并反思数学教学过程中的典型案例，将实践与理论结合起来，努力做好“理论的实践性解读”与“教学实践的理论性反思”.想来，不可能每位教师都成为所谓的特级或名师，但“作为研究者的教师”，应该是每位教师都可以和应该追求的.