一种角度加权的最小二乘目标定位算法

杜金香, 许恒博, 祝 鹏

一种角度加权的最小二乘目标定位算法

杜金香, 许恒博, 祝 鹏

(西北工业大学 航海学院, 陕西 西安, 710072)

在基于波达方向估计(DOA)的多传感器节点目标三维空间定位算法中, 当目标与传感器节点处于不同深度时, 定位原理决定了不同的俯仰角误差将导致不同的定位误差, 特别是当传感器与目标接近于同一平面，即俯仰角接近90°时, 较小的俯仰角误差将引起非常大的定位误差。为了解决该问题, 论文提出在最小二乘定位算法中, 根据不同俯仰角进行加权的方法, 降低俯仰角估计值接近90°的节点分量在定位方程中的贡献, 减少俯仰角估计误差对综合定位精度的影响, 提高定位算法对俯仰角估计误差的稳健性。文中对单个目标的定位进行了计算机仿真, 对比了某些节点深度与目标接近情况下加权最小二乘算法和最小二乘算法的定位性能, 仿真结果说明当参与定位的部分节点与目标深度接近时, 所提加权最小二乘算法对目标位置的估计均方根误差低于最小二乘算法, 具有更高的定位精度和稳健性。

传感器; 目标定位; 最小二乘; 加权最小二乘; 波达方向估计

0 引言

在众多水下无线传感器网络的定位算法中,根据在定位过程中有无利用距离信息可将定位算法分为基于测距的定位算法和无需测距的定位算法, 其中基于测距的定位算法精度较高[1-2]。基于测距的定位算法包括基于到达时间法(time of arrival, TOA)、基于到达时间差法(time different of arrival, TDOA)、基于波达方向估计(direction of arrival, DOA)以及基于接收强度(received signal strength, RSS)等的定位算法[3-8]。其中, 基于DOA的定位算法由于对时间同步的要求低并且可以工作在被动接收状态下, 非常适用于对非合作目标的定位。Wang等[6]推导了基于DOA的最大似然定位方法, 将角度估计值视为高斯分布的随机变量, 通过搜索似然函数的最大值估计目标的位置, 但仅给出了二维空间中目标的定位算法。徐济仁等[7]利用多节点测向信息采用最小二乘法进行目标定位, 但仅适用于二维平面的目标。倪忠德等[8]利用泰勒展开将非线性系统转化为线性系统, 并将各平台的量测误差作为权值引入到估计方程中, 利用最小二乘法进行定位, 缺点是忽略了非线性观测方程中的高阶特性, 因此定位精度不高。富森等[9]从非线性估计出发, 提出了基于牛顿迭代的最小二乘估计算法，保留了2阶甚至更高阶的观测误差, 提高了定位精度, 改善了定位结果的稳定性, 但仅给出了二维平面内的结果。金磊磊等[10]推导了三维空间中基于角度信息的点最小二乘目标定位方法, 并尝试融合TDOA和DOA 2种模态信息提高定位性能, 但是在最小二乘解中需要计算俯仰角的正切值, 而由于正切函数在90°附近的高度非线性导致较小的角度估计误差引起较大的正切值误差, 从而导致某些节点与目标位于相同或者相近深度时定位性能迅速下降。文中提出一种基于DOA量测值的加权最小二乘算法, 试图通过对不同节点的参数施加不同的加权系数, 降低算法对俯仰角误差的敏感性,提高算法的鲁棒性。

1 基于DOA的最小二乘定位方法

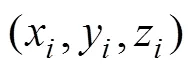
则目标角度信息和阵列节点坐标之间满足如下的几何关系

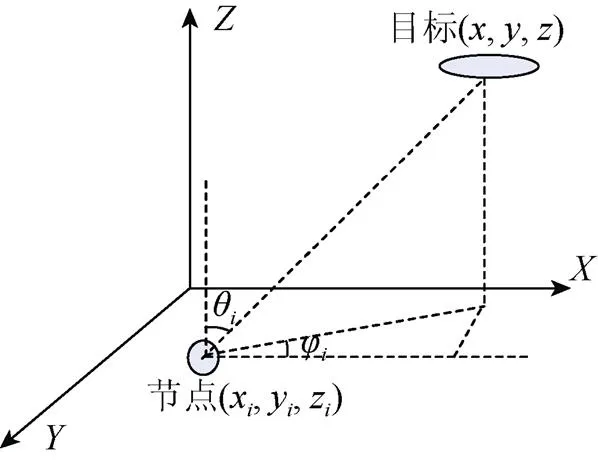
图1 目标与传感器阵列节点之间的位置关系

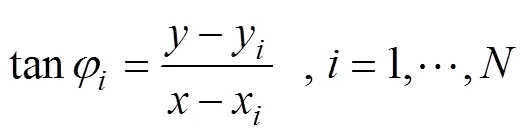
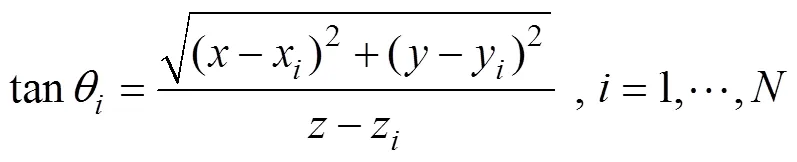
经过推导, 得到[8]

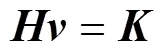
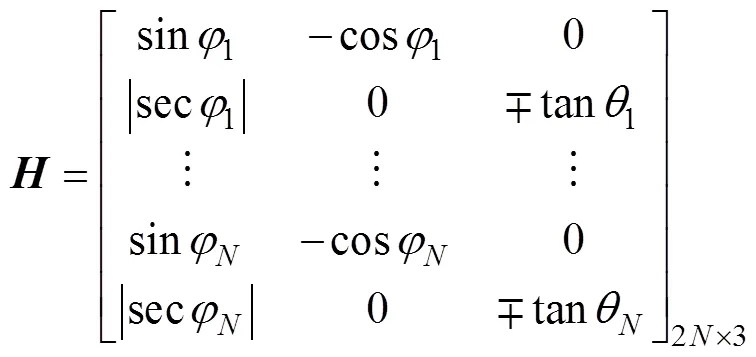
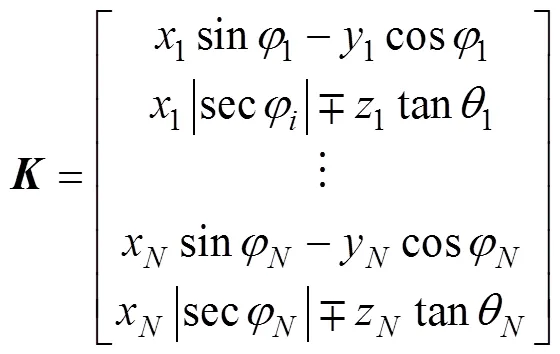
三维空间中基于DOA估计的目标位置最小二乘解[10]如下

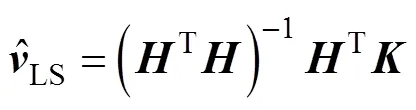
以上最小二乘解适用于传感器阵列节点与目标位于不同深度的情况, 此时俯仰角的正切值为有限大小。当某个或某几个传感器阵列节点与目标位于同一深度或者深度接近, 从而导致俯仰角等于或接近90°, 此时, 较小的角度估计误差即可导致俯仰角估计值的正切有较大的误差, 从而导致出现较大的定位误差, 定位性能下降。因此文中提出一种加权最小二乘方法, 对于俯仰角估计值接近90°的节点参数, 令其在整个定位方程中的权重较小, 从而减少该节点俯仰角正切值误差对整体定位性能的影响。

2 基于角度加权的最小二乘定位算法

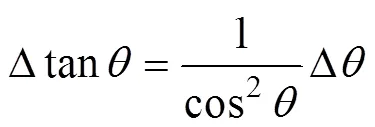
因此对于较小的角度估计误差, 当真实角度值越接近90°, 其正切值的估计误差越大, 即在90°附近的较小的俯仰角估计误差即可能引起巨大的正切值估计误差。当=0.01°时, 与角度的关系如图2所示。

因此提出一种加权最小二乘算法, 控制俯仰角度值接近90°时其正切值误差的负面影响。

将估计残差记为

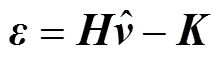
则优化的目标函数可以写作

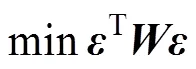
式中,为加权矩阵。通常加权矩阵应为正定矩阵, 选择为对角阵, 其第2-1和2个对角线元素对应第个节点参量加权值

对于俯仰角估计值, 如果有

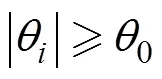
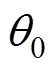
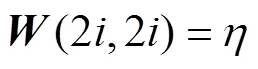
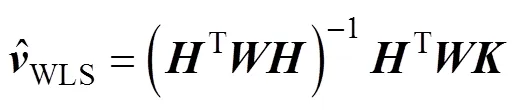
基于角度加权的最小二乘定位算法实现步骤归纳如下: 1)各个节点分别估计目标的方位角和俯仰角; 2) 根据俯仰角估计值的大小, 利用式(10)和式(12)设计加权矩阵; 3) 根据式(4)和式(5)计算系数矩阵和; 4) 根据式(13)计算目标位置的加权最小二乘解。

3 数字仿真和性能比较

进行计算机仿真试验, 比较基于角度信息的最小二乘方法和加权最小二乘方法的性能。

试验1: 边长1 km的正方形空间中随机布置6个传感器阵列, 目标深度100 m, 所有传感器的深度均在0~50 m范围内, 传感器阵列节点对目标的角度估计误差假设服从高斯分布, 其标准差在0.05~0.5之间取值, 每一种误差分布情况下进行1 000次蒙特卡罗试验, 分析2种定位方法对目标位置坐标估计的均方根误差, 结果如图3所示。

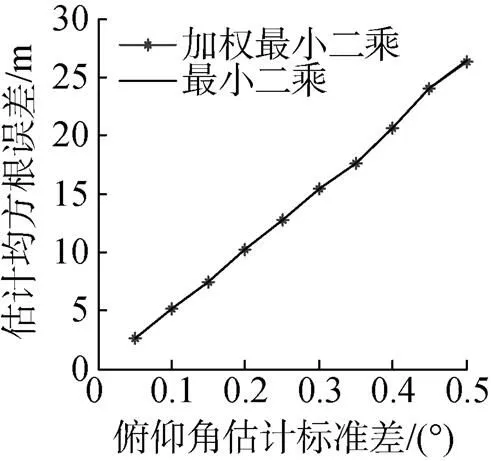
图3 无节点位置扰动时均方根误差比较(所有节点深度与目标深度差别较大)

由图3可以看出, 当传感器阵列节点的深度与目标深度差别较大的情况下, 基于角度估计信息的最小二乘法和加权最小二乘法估计性能几乎相同, 这是由于此时的值退化为单位阵, 加权最小二乘法退化为最小二乘法。

试验2: 在试验1条件基础上, 改变其中2个传感器阵列节点的深度, 使其与目标深度接近, 其余条件不变, 分析2种定位方法对目标位置坐标估计的均方根误差, 结果如图4所示。

由图4可以看出, 当某些节点深度与目标深度接近时, 加权最小二乘方法可以获得更小的估计均方根误差, 其定位性能优于最小二乘法。

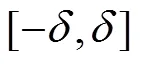
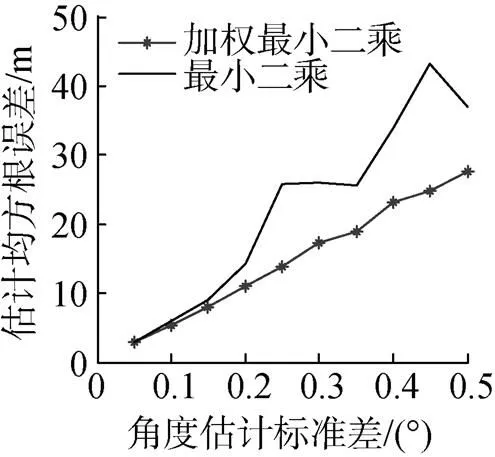
图4 无节点位置扰动时RMSE比较(某2个节点深度与目标深度接近)

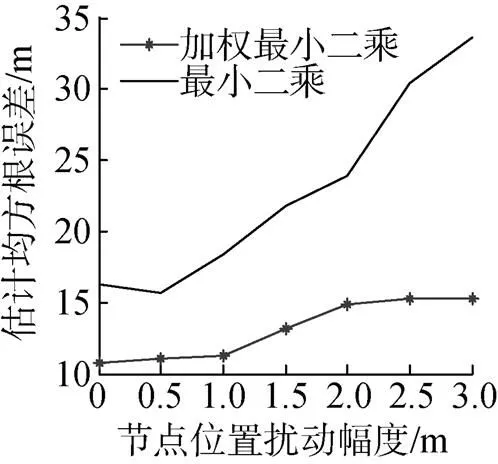
图5 节点位置扰动情况下2种方法的RMSE比较

由图5可以看出, 当节点位置存在误差时, 2种算法的定位均方根误差都有随着节点位置误差增大而增大的趋势, 定位性能下降。但是加权最小二乘方法的综合定位误差明显小于最小二乘法。

综合以上仿真试验结果可以看出, 采用加权最小二乘算法可以提高某些节点与目标深度相近情况下对俯仰角估计误差和节点位置误差的鲁棒性。

4 结束语

采用多个传感器阵列节点对目标角度的估计值对目标位置进行估计, 针对某个或某几个节点与目标深度接近时最小二乘法对俯仰角误差极度敏感的问题, 提出一种根据俯仰角估值大小进行加权的最小二乘定位算法, 提高算法对俯仰角误差的稳健性。对单个目标的定位进行了计算机仿真, 对比了某些节点深度与目标接近情况下加权最小二乘算法和最小二乘算法的定位性能, 仿真结果说明当部分节点与目标深度接近时所提加权最小二乘算法的稳健性更优。

[1] Vijay C, Winston K S, Yoo S C, et al. Localization in Underwater Sensor Networks—Survey and Challenges [C]//Proceedings of the 1st ACM International Workshop on Underwater Networks. Los Angeles, USA: IEEE, 2006: 33-40.

[2] Melike EＫ, Hussein T. A Survey of Architectures and Localization Techniques for Underwater Acoustic Sensor Networks[J]. IEEE Communications Surveys & Tutotials, 2011, 13(3): 487-502.

[3] Wang B, Li Y, Huang H N, et al. Target Localization in Underwater Acoustic Sensor Networks[C]//Proceedings of 2008 Congress on Image and Signal Processing. Sanya, China: IEEE, 2008: 68-72.

[4] Xu E, Ding Z, Dasgupta S. Source Localization in Wireless Sensor Networks from Signal Time-of-arrival Measurements[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2887-2897.

[5] Gholami M R. Gezici S. Ström E G. AConcave-convex Procedure for TDOA Based Positioning[J]. IEEE Communications Letters, 2013, 17(4): 765-768.

[6] Wang B, Yang G, Xie Z B, et al. Underwater Target Localization Based on DOAs of Sensor Array Network[C]//Procee- dings of 2nd International Conference on Signal Processing Systems. Dalian, China: IEEE, 2010: 238-240.

[7] 徐济仁，薛磊. 最小二乘方法用于多站测向定位的算法[J]．电波科学学报, 2001, 16(2): 227-230.Xu Ji-ren, Xue Lei. LS Algorithm Used in DF and Localization[J]. Chinese Journal of Radio Science, 2001, 16(2): 238-240.

[8] 倪忠德, 冯国华, 马宝华. 基于加权最小二乘法的多舰定位算法[J]. 北京理工大学学报, 2005, 25(11): 971-974. Ni Zhong-de, Feng Guo-hua, Ma Bao-hua. An Algorithm of Multiple-Vessel Localization Based on Weighting Least Squares[J]. Transactions of Beijing Institute of Technology, 2005, 25(11): 971-974.

[9] 富森, 孔祥维, 李哲, 等. 多基纯方位目标交叉定位中的非线性最小二乘方法[J]. 火力与指挥控制, 2009, 34(8): 80-83.Fu Sen, Kong Xiang-wei, Li Zhe, et al. Bearing-Only Target Cross Localization of Multi-Station based on Nonlinear Least Squares[J]. Fire Control & Command Control, 2009, 34(8): 80-83.

[10] 金磊磊, 梁红, 马艳. 基于水下无线传感器阵列网络多模态信息融合的目标定位[J]. 西北工业大学学报，2017, 35(6): 1020-1025. Jin Lei-lei, Liang Hong, Ma Yan. Target Localization of UWSAN Based on Multi-Modal Information Fusion[J]. Journal of Northwestern Polytechnical University, 2017, 35(6): 1020-1025.

An Angle Weighted Least Squares Algorithm for Target Localization

DU Jin-xiang, XU Heng-bo, ZHU Peng

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

In the three-dimensional localization algorithm based on direction-of-arrival(DOA), the target’s location errors are sensitive to the estimation errors of pitching angles, especially when the sensor array nodes are almost in the same horizontal plane with the target. In other words, the location errors are highly sensitive to the pitching angle errors when the pitching angles are close to 90°. To solve the sensitivity problem, a weighted least squares method is proposed in this paper. Small weighting factor is chosen for those sensor array nodes with large pitching angle estimation to decrease the impact of pitching angle estimation error and to increase robustness of the method. Furthermore, the performance of the weighted least squares method is analyzed via numerical simulation. Simulation results show that the present weighted least squares method has better robustness over DOA estimation errors and disturbance of the sensor array nodes than ordinary least squares method.

sensor; target localization; least square; weighted least square; direction-of-arrival(DOA)

TJ630.34; TB566; TN911.73

A

2096-3920(2019)05-0570-04

10.11993/j.issn.2096-3920.2019.05.013

杜金香, 许恒博, 祝鹏. 一种角度加权的最小二乘目标定位算法[J]. 水下无人系统学报, 2019, 27(5): 570-573.

2018-12-21

2019-02-20.

国家自然基金项目资助(61301197); 西北工业大学中央高校基本科研业务费基础研究基金(1069920140011); 水下信息与控制重点实验室开放基金(614221801040217).

杜金香(1977-), 女, 博士, 副教授, 主要研究方向为阵列信号处理、目标定位及水下声成像.

(责任编辑: 许 妍)