光电跟踪平台脱靶量滞后补偿方法

吕明明,侯润民,柯于峰,侯远龙

(南京理工大学机械工程学院,210094,南京)

光电跟踪平台通常利用可见光或红外图像跟踪器及伺服控制系统,来实现对目标的自动跟踪[1],广泛应用在火控、制导、靶场测试和激光通信等领域[2]。图像跟踪器根据所采集图像来计算目标相对视轴的偏差,即脱靶量,并结合光电平台的测角或测速传感器计算目标实际位置和速度。伺服控制系统以此来控制光电平台机构往偏差减小的方向运动,使目标始终处于视场中央。图像跟踪器在计算脱靶量时,需要经过图像信号的建立和处理、由跟踪算法提取目标位置以及信号传输等环节,因此脱靶量输出往往滞后于目标实际成像时间[3]。光电跟踪平台的主要任务就是捕捉和跟踪目标,而脱靶量的滞后会引起系统的超调和振荡,降低目标跟踪的精度,甚至导致目标捕捉和跟踪的失败。

由脱靶量的产生机理及处理过程可知,解决其滞后问题可以从以下3方面考虑:提高图像采集帧频,减少图像跟踪算法运算时间,利用预测模型直接或间接估计目标位置。伺服控制系统的输入是脱靶量与平台位置的合成值,因此用于脱靶量滞后的预测补偿分为合成前预测和合成后预测。合成前预测是指通过滞后脱靶量直接估计目标不含滞后的脱靶量,再将预测值与平台位置合成[4-6],而合成后预测是指先人为将平台传感器的反馈值延迟,使其与脱靶量在时间轴上保持一致,再通过合成值进行估计伺服控制系统的输入值[7]。

脱靶量滞后是光电跟踪系统中不可忽视的问题,如何进行补偿一直是国内外研究的热点。文献[4]利用线性Pade逼近分析光电成像传感器的纯延迟,并采用卡尔曼滤波的多步预测法来补偿脱靶量滞后。文献[5]提出自适应卡尔曼滤波算法的模型,用其估计目标角速度,并前馈到速度回路,实现光电跟踪平台的复合控制。文献[6]针对光电平台跟踪器延迟,采用基于自适应最小均方差(LMS)算法,结合图像信息和无人机信息,实现对控制信号的有效预测。文献[8]建立基于鲁棒H∞滤波算法的“当前”统计模型,解决图像跟踪器的脱靶量滞后和信号噪声问题。文献[9]提出脱靶量延迟具有不确定有界时变的特性,并在此基础上利用基于统计Singer模型和H∞控制对滞后进行补偿。上述文献均采用合成前预测,而文献[7]作为典型的合成后预测法,提出人为将光电平台的测角传感器信号延迟再与脱靶量合成,之后使用卡尔曼滤波进行外推,解决了脱靶量滞后问题。

非线性跟踪微分器(NTD)是由中国科学院韩京清研究员等针对微分信号的精确提取所设计[10],可以较好地跟踪被噪声污染的输入信号,同时利用积分运算提取其近似微分信号,目前已在信号滤波[11]和微分信号提取[12]等方面广泛应用。本文在将脱靶量滞后等效为纯延迟环节和采样保持环节的串联的基础上,分别利用直接预测补偿法和机动目标的“当前”统计模型(CSM)进行补偿,其中,直接预测补偿法估计无滞后脱靶量的前提是利用NTD提取滞后脱靶量的跟踪及微分信号。

1 脱靶量滞后问题描述

光电跟踪平台的主要任务是捕捉、锁定和跟踪目标。光电跟踪平台的工作示意图如图1所示,其主要由图像跟踪器、伺服控制系统和平台负载等构成。在自动跟踪目标时:图像跟踪器通过采集的图像计算目标脱靶量,并与平台位置合成;伺服控制系统将合成值作为输入信号,形成随动控制系统,控制平台机构往脱靶量减小的方向运动,从而让视轴始终指向目标。

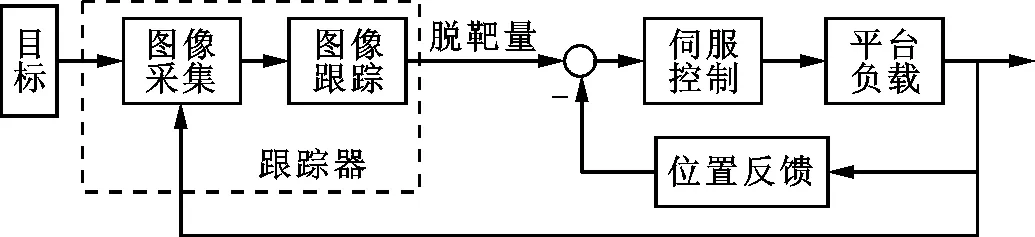
图1 光电跟踪平台工作示意图

在脱靶量计算过程中,可见光或红外传感器生成图像、目标跟踪算法运行、数据传输等环节都需要一定的时间,使得伺服控制系统得到的脱靶量严重滞后于目标当前位置,这对系统的稳定性和跟踪精度都有着不利的影响。考虑脱靶量延迟的跟踪系统结构图如图2所示,脱靶量滞后相当于在伺服控制系统的位置回路中串联了一个纯延迟环节和采样保持环节。

θT:目标位置;θO:平台反馈位置;τ:脱靶量滞后时间;τ0:采样保持时间;Gp(s):位置校正环节;Gv(s):速度回路的等效传递函数;s:拉普拉斯变换的复变量图2 考虑脱靶量延迟的跟踪系统结构图

文献[13]在假设脱靶量滞后时间为一帧时间的前提下,进一步推导了图像跟踪器的帧频与位置带宽之间的关系,公式为

(1)

式中:fT为图像跟踪器帧频;fP为位置带宽;θ0为不考虑滞后的位置环相角裕度;θ1为引入滞后的相角裕度。由此可知,脱靶量作为伺服控制系统位置回路的误差比较环节,其滞后严重影响了控制系统的相位裕度,导致系统超调量的增加和位置环最大带宽的降低,使跟踪系统会产生振荡,降低了跟踪精度,甚至会导致目标捕捉和跟踪的失败。

2 基于NTD和CSM的补偿方法

2.1 非线性跟踪微分器

非线性跟踪微分器是自抗扰控制器的重要组成部分,设计的初衷是从不连续或带有随机噪声的信号中提取连续信号和微分信号[12]。

令z2为信号z1的微分信号,构建系统[10]为

(2)

若式(2)的所有解(按菲利波夫意义)都有界,且满足

(3)

那么对任意有界可测信号v(t),t∈[0,∞)和任意T>0,有微分方程

(4)

式中:x1为v的跟踪信号;x2为x1的微分信号。x1(R,t)满足

(5)

通过选择适当的非线性函数f(·)和参数R,使x1(t)充分逼近输入信号v(t),同时得到输入信号广义导数的一种光滑逼近信号x2(t)。NTD通过积分运算得到输入信号的微分形式,避免了传统差分带来的噪声放大效应。文献[10]给出了NTD的严格数学证明。理论上,通过多个NTD的串联,可以得到输入信号v(t)的二阶或更高阶微分信号[11]。

采用不同的离散方法,NTD会有不同的形式。常用的基于欧拉法的NTD离散形式[14]为

(6)

式中:v(k)为输入信号;h为步长,由系统运算周期决定;h0和r0分别为滤波因子和速度因子,影响NTD的滤波性能和跟踪速度,通过设置合理的h0和r0,可以得到输入信号v(k)的跟踪及微分信号,通常将h0取为h的若干整数倍[14];L(Δx,x2,r0,h0)为最速综合函数,计算式为

(7)

2.2 延迟环节补偿

卡尔曼滤波是光电跟踪平台常用的脱靶量滞后补偿方法[15-17],然而卡尔曼滤波需要假设信号动态性能及噪声统计特性已知,但实际情况并不能完全满足[18],限制了补偿效果。本文采用直接预测法补偿延迟环节,其补偿原理如图3所示。

θ:目标脱靶量;θτ:滞后脱靶量;补偿后的脱靶量图3 脱靶量滞后补偿原理

(8)

由式(8)可知,想要利用直接预测法补偿滞后脱靶量,就需要首先提取滞后脱靶量的跟踪及微分信号。直接通过差分得到的微分信号存在噪声放大效应,并且滞后时间越小,噪声放大越严重,完全可能淹没微分信号[19]。因此,采用式(6)(7)计算滞后脱靶量的跟踪及微分信号。

结合式(6)(8),可得出基于NTD的滞后脱靶量直接预测补偿表达式为

(9)

式中:λ为预测因子,可预先设定;速度因子r0决定了跟踪速度的快慢,r0越大跟踪速度越快,但引入的随机噪声也会越大;滤波因子h0影响着滤波效果,实际上NTD的滤波效果与h0的开方成反比[20],但h0过大会增加相位的损失,因此参数调整要综合考虑两方面的性能。

由于目标机动性的增强,光电跟踪平台必须根据被跟踪目标的变化实时调整NTD参数,以得到精准的跟踪及微分信号,从而获得满意的脱靶滞后补偿效果。当跟踪信号x1和输入信号v的间距充分小时,其微分数值充分接近[21],因此可以用间距来调整NTD的参数。进一步,为了降低信号随机误差的影响,采用前M个信号的间距均值来自适应调整r0和h0,计算式为

(10)

式中:M为参考的周期数;kr0和kh0分别为速度因子r0和滤波因子h0的控制增益系数,需要预先设定。

2.3 采样保持环节补偿

CSM是一种描述目标机动特性的实用模型,其假定目标在下一时刻的加速度有限,只能是在“当前”时刻加速度的邻域内[5]。CSM的离散状态方程为

(11)

(12)

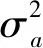
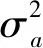
(13)

式中a+max和a-max分别为机动目标的最大正负加速度。

实际光电跟踪平台中,图像跟踪器帧频不超过100 Hz,远小于平台位置反馈采样频率(约800 Hz)[13]。在计算相邻两次脱靶量期间,系统会有N个平台传感器的反馈数据,相当于伺服控制系统中包含一个采样保持环节,且

(14)

式中:[·]为取整函数;T为平台位置反馈采样周期。

本文利用式(11)估计在采样保持期间每个系统周期的脱靶量,其中k=1,2,…,N,此时F(k)和U(k)表达式详见文献[22]。

3 验证实验与结果

3.1 延迟环节补偿实验

为了验证本文所提出的脱靶量滞后补偿方法中延迟环节的补偿效果,假定目标以θ=10sin(0.8t)做等效正弦运动,对输入信号人为延迟并补偿,进行了25 s的仿真实验。NTD的参数设定如下:h=0.001 25 s,r0=1 000,h0=0.015,并根据式(10)实时调整r0和h0,M=5,kr0=0.1,kh0=0.1,τ=0.03 s。

图4 NTD跟踪及延迟环节的补偿结果

图4是NTD跟踪及延迟环节补偿结果,可以定性地看出,跟踪信号能够很好地跟踪滞后的脱靶量,直接预测法利用滞后跟踪信号和微分信号,很好地还原了目标输入信号,实现了延迟环节的补偿。图5是NTD跟踪及延迟环节的误差,通过定量分析可知,除了在初始阶段因信息量不足出现较大误差外,其余时间的跟踪误差范围是[-0.24°,0.24°],脱靶量延迟环节的补偿误差范围是[-0.15°,0.29°]。进一步,计算出跟踪误差的均方根误差为0.18°,补偿误差的均方根误差为0.21°。

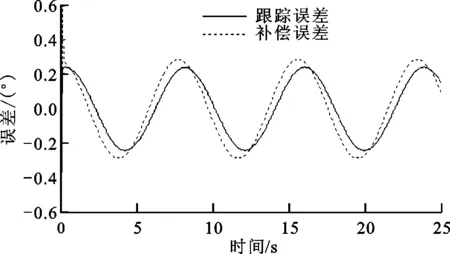
图5 NTD跟踪及延迟环节的误差

3.2 采样保持环节补偿实验

将3.1节中脱靶量延迟补偿后的信号作为输入信号,进行25 s的仿真实验。采样保持环节补偿的参数设置如下:T=0.001 25 s;采样保持周期为0.03 s;式(12)中的机动频率α=0.001 s-1;式(13)中的a+max=0.64 (°)/s2,a-max=-0.64 (°)/s2。

图6是采样保持环节的补偿效果。可以看出,本文方法在采样保持期间,很好地跟踪了输入信号,能够符合目标的机动规律。图7是采样保持环节的补偿误差,可定量分析出采样保持环节的补偿误差范围为[-0.54°,0.65°],均方根误差为0.16°。

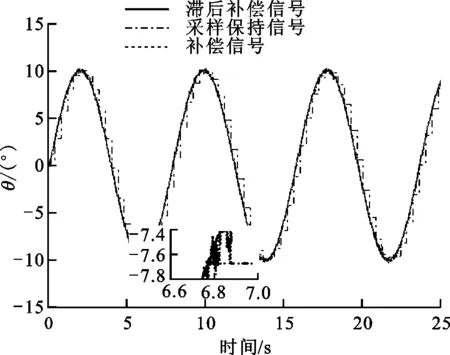
图6 采样保持环节的补偿效果

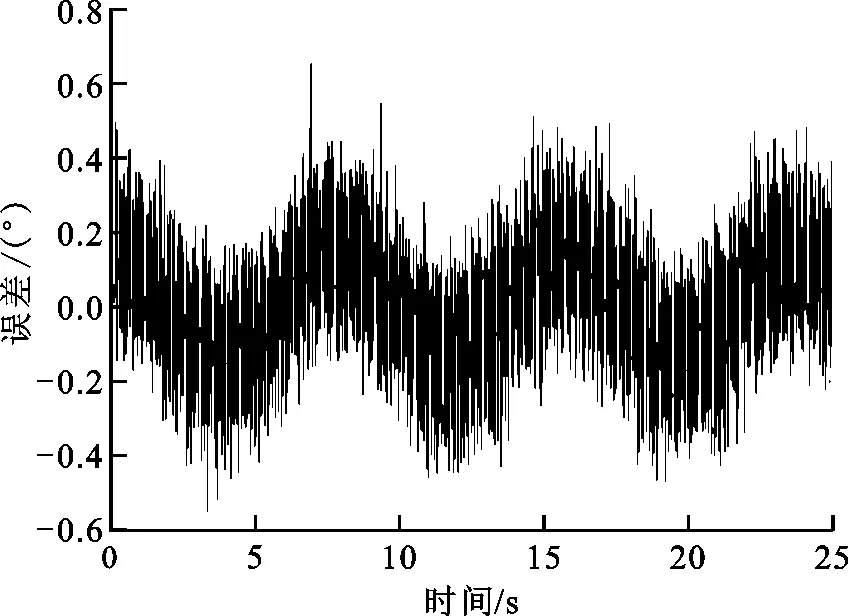
图7 采样保持环节的补偿误差

3.3 综合补偿实验

以某型光电跟踪平台的高低方向进行实验,模型结构如图2所示,其中位置校正环节Gp(s)和速度回路等效传递函数Gv(s)分别为

(15)

(16)

采用基于卡尔曼滤波(Kalman)和基于自适应LMS的补偿方法,与本文提出的基于非线性跟踪微分器与“当前”统计模型的补偿方法(NTD-CSM)进行对比,单位阶跃响应的超调量和调节时间的对比如表1所示,单位阶跃响应前3 s的曲线如图8所示。可以看出:3种方法的调节时间相差不多,体现了光电跟踪平台在目标出现时快速准确的捕捉性能,NTD-CSM补偿法阶跃响应基本无超调,远小于Kalman和LMS两种方法。

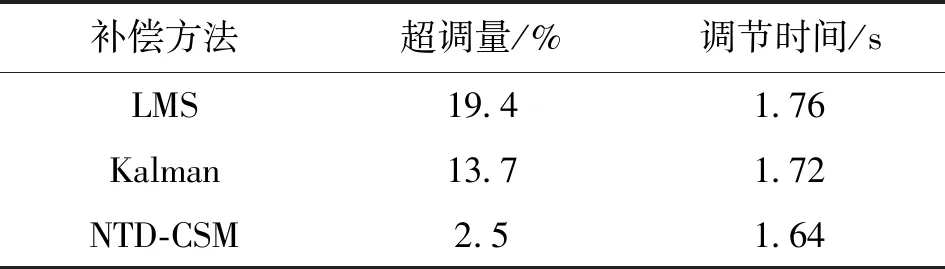
表1 单位阶跃响应的结果对比

图8 3种方法单位阶跃响应曲线的比较

图9 3种方法目标跟踪曲线的比较

为验证所设计的脱靶量滞后补偿方法在目标跟踪上的表现,仍在该平台上假定目标以θ=10sin(0.8t)做等效正弦运动,并加入幅值为1°的随机噪声,同样进行了25 s仿真实验。图9是3种方法的目标跟踪曲线,可以看出,LMS的误差范围为[-0.44°,0.52°],Kalman的误差范围为[-0.49°,0.58°],NTD-CSM的误差范围为[-0.33°,0.47°]。图10给出了3种方法的均方根误差曲线,为了突出比较结果,只取前2 s的均方根误差数据绘制曲线,可以明显看出,NTD-CSM的跟踪精度优于Kalman和LMS的。

图10 3种方法均方根误差曲线的比较

4 结 论

(1)本文提出了一种用于解决光电跟踪平台中目标脱靶量滞后的补偿方法。根据脱靶量滞后可以等效为纯延迟环节和采样保持环节,分别采用非线性跟踪微分器和机动目标“当前”统计模型进行补偿。

(2)借助非线性跟踪微分器获取脱靶量滞后信号的跟踪信号和微分信号,并采用直接预测补偿法进行延迟环节的补偿。由实验可知,跟踪信号及补偿信号的均方根误差分别为0.18°和0.21°。

(3)建立机动目标“当前”统计模型的离散状态方程,并采用修正的瑞利分布描述加速度的“当前”概率密度,从而实现采样保持环节的补偿。实验分析表明,采样保持环节补偿的均方根误差为0.16°。

(4)建立综合补偿实验模型,对比所提方法与基于自适应方差的补偿方法及基于卡尔曼滤波的补偿方法。在不影响调节时间的前提下,单位阶跃响应的超调量由19.4%和13.7%降低至2.5%。在实际应用中应综合考虑超调量和调节时间。