用于稳态视觉诱发电位脑机接口目标识别的深度学习方法

杜光景,谢俊,张玉彬,曹国智,薛涛,徐光华

(西安交通大学机械工程学院,710049,西安)

脑-机接口(BCI)是一种不依赖于大脑正常输出通路(外周神经和肌肉组织)而直接实现大脑与计算机等外部设备进行通信的技术[1]。该技术为重度瘫痪病人提供了通过大脑意念操控轮椅[2]、进行假肢控制[3]等全新的与外界环境进行交流和控制的手段,脑-机接口技术还被应用于虚拟现实[4]、军事[5]、航天[6]等领域。稳态视觉诱发电位(SSVEP)是大脑视觉系统对外部周期性视觉刺激的响应,由于其具有稳定性强、操作简单等优势,成为一种被广泛应用的脑-机接口信号类型[7-8]。但是,由于SSVEP属于微弱信号,容易受到肌电、自发脑电等背景噪声的影响,导致其识别困难。

传统的SSVEP信号分类一般通过手工提取脑电信号的频域或时频域特征信息,然后对特征向量进行有监督分类的方式来实现的。吴平东等运用叠加平均与快速傅里叶变换结合的方法,在频域上对SSVEP进行分类,该方法需要对多次视觉刺激下的脑电信号进行平均,限制了其实用性[9]。徐光华等设计了一种高频组合编码SSVEP范式,并针对组合编码刺激产生的变频脑电信号,提出基于改进希尔伯特-黄变换的变频脑电信号特征提取与局部频谱极值目标识别方法[2]。该方法虽然可以利用高频组合编码呈现更多的刺激目标,但其刺激时间及识别正确率仍有待优化。高小榕等利用典型相关分析(CCA)方法,对多通道时域脑电信号与正、余弦波形组成的模板信号进行相关分析,有效地提高了识别正确率[10],但是其模板信号相对固定,未考虑到使用者的个体差异性。

相比于传统方法,深度学习不需要手工提取特征,能够直接从原始数据中自动学习特征,可有效避免人工特征提取过程中导致的信息丢失。深度学习已经在语音识别[11]、图像识别[12]等领域展现出了巨大优势。安秀等使用深度置信网络(DBN)对左右手运动想象进行了分类,其分类精度要明显高于支持向量机(SVM)等传统方法[13];Tabra等利用卷积神经网络(CNN)对运动想象脑电信号的时频图进行识别,并使用BCI竞赛公开数据集进行了分类研究,结果表明相比于竞赛获胜算法,该方法具有更好的分类表现[14]。基于SSVEP的脑-机接口具有刺激目标多、信号时空域特征不明显等特点,因此分类过程也有较大差别,目前应用于SSVEP目标识别的深度学习方法较为有限。

为了解决因SSVEP信号信噪比低、非平稳、个体差异性强等因素引起的脑-机接口系统应用中目标识别困难等问题,本文引入深度学习中的卷积神经网络,提出了基于卷积神经网络的SSVEP信号识别分类方法。该方法以多通道原始脑电信号为输入,根据SSVEP信号兼具时、频、空域特征的特点,提出先时域后空域卷积的时空分离卷积操作,首先应用一维卷积核对各通道进行时域卷积,然后将卷积后的各通道信息融合,进行空域卷积,随后采用多尺度卷积Inception模块[15]来提取融合后不同尺度的特征信息。分类结果表明,本文所提方法对SSVEP信号分类的准确率和速度均有明显提升。

1 构建深度学习网络

1.1 卷积神经网络

CNN是深度学习应用最为广泛的神经网络之一,在人脸识别、车牌号识别、文档分析等领域得到了成功的应用。CNN最早由Fukushima提出,由Lecun等对其进一步完善,典型的CNN网络结构一般包括卷积层、降采样层、全连接层等[16]。

卷积操作使用滤波器(卷积核)对上一层输入进行卷积变换,采用局部感受野和权值共享思想,大大降低了网络参数的数量。l层卷积层上的第j个节点Xl,j可以通过如下卷积操作得到

(1)

式中:l为卷积所在层数;Mj为输入的第j特征图;K为卷积核;B为l层的偏置;f为激活函数;*表示卷积操作。

降采样可降低输入维度,从而降低网络复杂度,同时可降低过拟合的风险。降采样层上节点X的计算公式为

Xl,j=f(βl,jdown(Xl-1,j)+Bl)

(2)

式中:β为下采样系数;down为下采样函数。

输出层对前面各层提取的特征进行分类,利用softmax函数计算最后输出被分到每个类的概率,计算方法为

(3)

式中:ZY为输出层前级输出单元的输出;Y为类别索引;c为总的类别数;P(Y|X)表示输入X属于类别Y的概率。

图1 卷积神经网络结构示意图

1.2 深度学习网络的构建

针对SSVEP原始信号兼具时、频、空域特征的特点,本文设计了一种先时域后空域卷积的时空分离卷积的CNN结构来对SSVEP信号进行识别。本文采用的CNN网络结构如图1所示,整个网络由7层网络组成:第1层为输入层,第2层、3层为卷积层,第4层为降采样层,第5层为Inception层,第6层为降采样层,第7层为输出层。各网络层具体如下。

(1)输入层l1。该层为网络的输入层,输入原始的多通道SSVEP信号,具体输入样本矩阵大小为通道数×数据采样长度,在图1中,输入样本为6×1 200,表示输入数据为6个通道,1 200个采样点,即采样率为1 200 Hz下的1 s数据。

(2)卷积层l2。该层有6个一维卷积核,主要用来对输入的SSVEP信号进行时域滤波。卷积核大小为1×300,6个卷积核对输入矩阵进行时域卷积,可以得到6个特征图。卷积操作时,步长为1,进行边界补零操作,因此每个特征图的大小为6×1 200。

(3)卷积层l3。该层有12个一维卷积核,主要用来对上一层的输出进行空域卷积。卷积核大小为6×1,输出为12个特征图。卷积操作时,步长为1,无边界补零操作,输出的特征图大小为1×1200。使用线性整流函数(ReLU)作为激活函数,不使用偏置。

(4)降采样层l4。该层采用12个大小为1×4的卷积核对卷积层l3的输出进行降采样处理。降采样采用平均池化方法,步长与卷积核大小一致,因此输出12个特征图,大小为1×300。

(5)Inception层l5。该层同时使用1×16、1×8等不同大小的卷积核进行多尺度卷积,以提取不同尺度的特征,在1×16、1×8的卷积核前以及1×8的最大池化卷积核后分别使用一个1×1的卷积核,用来降低维度,减少参数和计算量。每种卷积核的数量都为4个,因此最后特征连接后的大小为12个1×300的特征图。

(6)降采样层l6。该层采用12个大小为1×6的卷积核对Inception层的输出进行降采样处理。降采样采用平均池化方法,步长与卷积核大小一致,因此输出12个1×50的特征图。同时使用dropout方法防止过拟合。最后将降采样后的数据进行扁平化处理,使多维数据变为一维向量。

(7)输出层l7。该层有4个节点,代表四分类问题(对应4个不同的SSVEP刺激频率)。将池化层输出的一维向量与输出层节点全连接,使用softmax函数计算输入对应分类标签的概率分布。

同时,为了加快训练收敛速度,对网络中每个卷积操作后的数据均进行批标准化处理。

1.3 网络的学习过程

CNN的训练过程主要采用误差反向传播算法,即先计算训练数据在网络中前向输出的值与期望输出值之间的误差,然后将误差反向传播,对误差求各个权值和偏置的梯度,由此来调整各权值和偏置,进行网络学习。

本文网络的训练过程采用小批量训练,每次训练输入批量数据大小为32个样本。权值的优化调整采用Adam随机梯度下降法[17],学习率设置为0.001,一阶矩估计的指数衰减率设置为0.9,二阶矩估计的指数衰减率设置为0.999。网络的初始化权值服从均值为0,标准差为1的高斯分布。为防止网络过拟合,训练过程中加入dropout方法,即每次更新权值时随机使一些节点失效,不进行权值更新。本文设置dropout比率为0.5。最大迭代次数设置为400,通过训练过程的验证集损失曲线来判断模型是否训练终止。

1.4 基于CNN的SSVEP目标识别

基于CNN的SSVEP目标识别分为如下4个步骤:

(1)采集被试者在不同目标刺激下的SSVEP多通道信号,作为网络输入;

(2)为采集到的数据制作标签,并将数据集随机划分,其中数据集的60%为训练集,20%为验证集,20%为测试集;

(3)进行模型训练,将训练集、验证集数据输入网络,训练集进行网络训练,验证数据集用来进行模型最优参数选择;

(4)将训练好的模型用来对测试集的数据进行分类,得到SSVEP目标识别的准确率。

SSVEP分类流程图如图2所示。

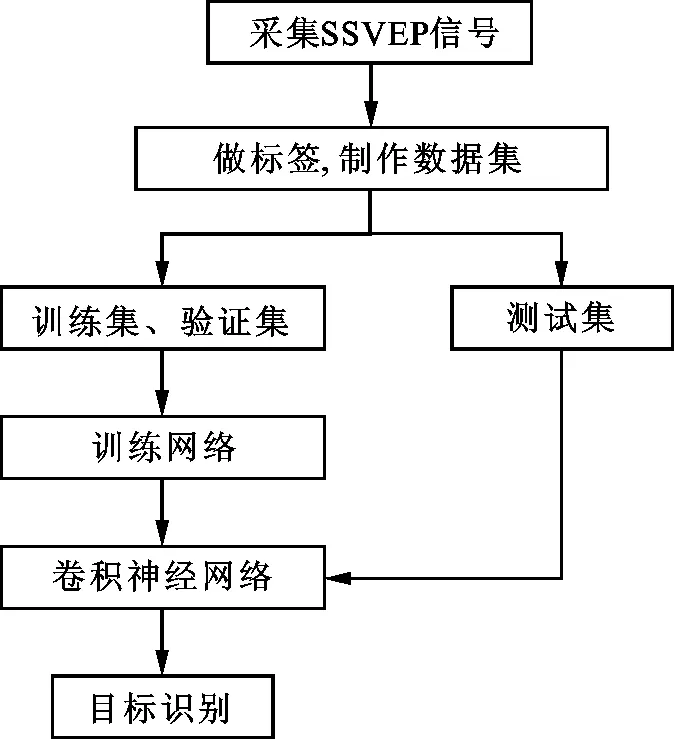
图2 基于CNN的SSVEP分类流程图

2 实验与分析

2.1 脑-机接口范式设计

为了验证本文提出的方法对SSVEP脑-机接口目标识别的实际效果,设计了周期运动的棋盘格刺激范式[18],如图3所示,图中共4个刺激目标,分别以频率为6、7、8、9 Hz进行收缩与扩展运动以诱发SSVEP信号。实验中刺激目标呈现在显示器上,显示器分辨率为1 920×1 080像素,刷新率为144 Hz。该刺激的制作与呈现控制均由基于Matlab环境的Psychophysics Toolbox工具箱实现。

图3 基于运动翻转棋盘格的刺激范式

2.2 实验过程

实验招募了7名身体健康、正常视力或矫正视力正常的被试者(S1～S7)进行实验,被试者中有5名男性,2名女性。实验在安静的房间中进行,被试者端坐在离显示器约80 cm处,在每轮实验中,被试者被要求注视显示器上的特定目标,避免身体的移动。每名被试者依次注视以6、7、8、9 Hz运动的刺激目标,每个刺激目标呈现80次,每连续20次为一轮,每轮实验后给予被试者一定的休息时间。每轮实验的时序安排如图4所示,每轮刺激中,单次刺激目标呈现的时间为5 s,随后显示器灰屏1 s,然后进行下一次刺激呈现。

图4 刺激时序图

2.3 信号采集

脑电信号的采集使用奥地利的g.USBamp脑电信号采集系统,采样率为1 200 Hz。根据国际标准10/20系统法采集视觉区的PO3、POz、PO4、O1、Oz、O2共6个通道的脑电信号。接地电极在前额的Fpz处,参考电极在右耳乳突A1处。单次采集的脑电数据如图5所示,数据大小为6×6 000,6为采集的6个通道,6 000为1 200 Hz采样率下5 s数据,即1 200×5=6 000。

图5 6通道脑电数据波形图

2.4 分类方法

为了验证该方法的有效性,本文还采用了下列方法对相同的数据集进行分类作为对比。

(1)CCA方法[8]。将原始信号直接使用CCA方法进行分类,由于原始信号SSVEP的频谱只在基频处有明显波峰,因此设置CCA方法中的谐波个数为1。

(2)CCA结合SVM方法[19]。将用CCA方法对训练集得到的相关系数输入到SVM中训练,然后用测试集进行测试。分类器选用径向基核函数,参数寻优采用LIBSVM工具箱[20]的网格搜索算法。

此外,除了使用识别准确率来评价脑-机接口的性能,本文还引进信息传输率(ITR)评价方法。每分钟平均传输的信息量定义为

(4)

式中:K为可选目标数;T为识别一次刺激所需时间;A为识别准确率。

2.5 结果分析

在CNN训练阶段,对每个被试单独训练。为了得到被试者在较短时间刺激下的识别准确率,取单次刺激的前3 s数据,并将数据截取为前0.5 s、前1 s、前1.5 s、前2 s、前2.5 s以及前3 s的数据长度进行分析,即输入样本矩阵大小分别为6×600、6×1 200、6×1 800、6×2 400、6×3 000、6×3 600。网络训练使用Keras深度学习框架,所用计算机CPU为Intel(R) Xeon(R) E5-2630 v4 @ 2.20 GHz,内存为64 GB,GPU为 NVIDIA GTX 1080Ti。6种不同输入数据长度的训练时间分别约为130、152、183、229、275、293 s。

(a)S1 (b)S2

(c)S3 (d)S4

(e)S5 (f)S6

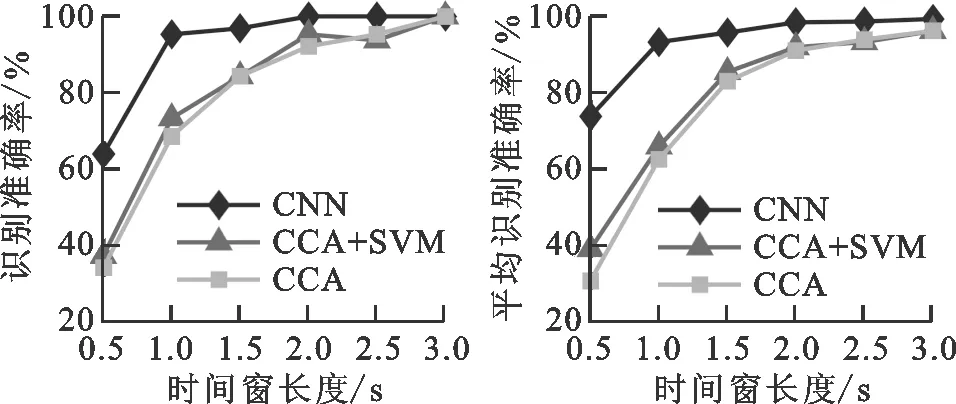
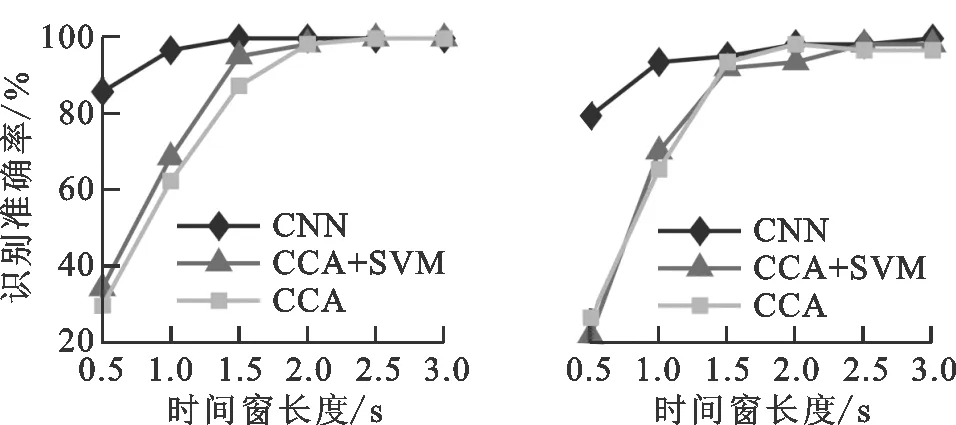
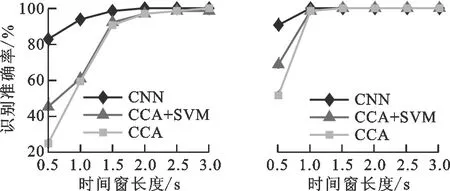
(g)S7 (h)平均识别准确率图6 采用3种方法对7位被试者的识别准确率比较

被试者S1～S7在不同时间窗长度时,分别采用CNN方法、CCA方法以及CCA结合SVM方法的单被试识别准确率以及多被试平均识别准确率如图6所示。对比本文所提方法与另外两种方法在不同时间窗长度的平均识别率实验结果,可知在各个不同的时间窗长度时,本文方法表现优异,尤其在0.5～2 s这种时间窗较短且频率特征不明显的情况下,本文方法要明显优于另外两种方法。在时间窗长大于2 s时,此时频率特征已比较明显,对被试者S1、S2、S3,3种方法识别准确率均能达到96%以上,并无较大差异。在时间窗为1 s时,相较于另外两种方法,本文方法对多被试平均识别准确率的提升分别为48.73%和41.21%,且此时采用本文方法的多被试平均识别准确率为93.3%～5.16%,已达到较高的识别准确度,可较好满足实际工程应用要求。结果表明,本文方法对于较短刺激时间的目标识别具有明显的提升效果,可提高脑-机接口系统的识别效率。

对于不同被试者,本文方法均能在短时间窗时提高其识别准确率,并无明显的个体差异性。对于被试者S1、S2、S3、S5、S6、S7,本方法对其在0.5、1 s时的准确率提升均达到了30%以上。对于本身SSVEP响应特征较为明显的被试者S4,本文方法对其识别率提升有限,但是在1 s长度的时间窗时,本文方法的识别准确率已达到100%。图7为被试者S1在1 s时间窗长度时用本文方法分类的混淆矩阵。可知对各频率的识别率均较好,尤其对6、9 Hz的刺激目标识别率均达到了100%。

不同被试者采用本方法在1 s时间窗长度时的识别准确率及信息传输率如表1所示。本文方法在1 s时间窗长度时平均正确识别率为93.3%,平均信息传输率为94.17 b/min。实验结果表明,本文方法对基于SSVEP脑-机接口系统的目标识别有较高准确率与信息传输率,增强了脑-机接口的应用性能。

图7 被试者S1识别准确率混淆矩阵

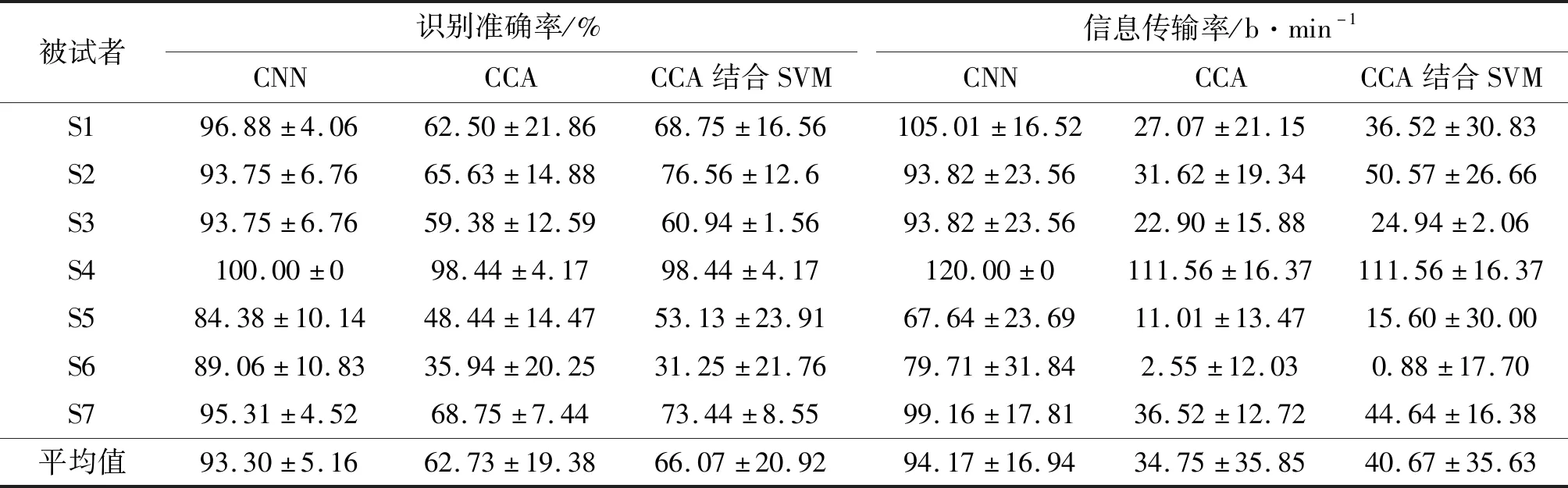
表1 采用3种识别方法对被试者在1 s时间窗长度时识别准确率及信息传输率

3 结 论

针对SSVEP信号存在信噪比低、非平稳、个体差异性强等特点导致脑-机接口目标识别准确率低等问题,本文提出了一种基于CNN的单次SSVEP信号识别方法。该方法具有自适应提取信号特征的特点,不需要人工预处理,同时可以通过对数据的学习,更好地适应个体差异性。实验结果表明,该方法对于运动翻转棋盘格刺激的目标识别准确率及信息传输率均要明显高于无训练CCA方法和有训练CCA结合SVM方法。对于不同被试者,本方法在1 s时间窗长度时识别准确率均在80%以上,信息传输率在65 b/min以上,表明本方法对于较短时间刺激,具有明显的识别优势,同时具有较高的鲁棒性。该方法可实现SSVEP信号的精确识别,同时具有较高的信息传输率,提高了脑-机接口系统的应用性能。

后续的研究将在现有工作基础上,尝试使用迁移学习对未训练被试者进行目标识别,提高网络模型在不同被试者之间的泛化能力;同时增加分类的数目,对更复杂的多分类SSVEP进行研究,将该方法应用于在线目标识别,提高其工程实用价值。