基于ANSYS/LS-DYNA的岩石爆破结构数值模拟分析

孙西濛， 叶春琳， 胡燕川， 张 凯， 刘宝林， 薛启龙， 周 鹏

(1.北京市政路桥股份有限公司，北京 100045； 2.中国地质大学〈北京〉工程技术学院，北京 100083； 3.自然资源部深部地质钻探技术重点实验室，北京 100083)

0 引言

随着时代的进步和城市化进程的加快，地下空间的利用已然成为未来发展的趋势。在地下空间的综合开发利用过程中，爆破技术是一种相对经济合理的施工方法。随着煤矿行业的迅速发展，我国爆破技术不断发展，目前,我国用于破碎岩石的方法主要有爆破法和机械破岩法，这两类方法应用最广,而其他破岩方法只是作为破岩的一种辅助手段。建立在机械钻孔、往孔内装入待爆炸药的常规爆破破岩方式以综合效率高在较长时期内占据着相当重要的地位,但该方法存在对原岩的扰动性大,易造成周边岩石破坏,存在支护困难,破碎岩石块度不均匀,它必须依靠钻孔、装药和爆破等多种工序操作,而且装药和爆破过程实现机械化和自动化难度较大等问题。克服常规爆破破岩的缺点,机械破岩得到了快速发展,在采矿、选矿、石材加工、隧道掘进、石油钻进方面已得到了广泛应用[1]。但机械破岩也有其局限性,因此出现了许多现代的非机具破岩方法，如:超声波法、水射流法、射弹冲击法、水电效应法、火花放电法、等离子体法、电子束法(聚焦电子束、脉冲电子束、高能加速器)、激光法、红外线法、热熔法(电能、核能)、高频法、电热核法、微波法及化学破碎法等。其中等离子爆破技术也逐渐试用，该技术是以高功率电脉冲技术与放电等离子体为基础，将电能和化学能转换为冲击波机械能，借助于脉冲功率源的重复运行，在一定的区域内产生可控的重复强冲击波，进而破碎岩石[2]。等离子法在坚硬岩石中穿凿炮孔较机械法速度快，而成本只有机械法的一半，有望成为一种简单易行，经济高效环保的新型实用破岩新工具，具有很高的应用前景[3]。作为一种新型爆破技术，其爆破孔的设计对整个爆破效果及爆破效率起决定性的作用。

爆破工程技术是一门相当古老的学科，是利用爆炸能量，使爆炸对象发生变形，破碎移动，达到预期目的一门技术，其理论基础是爆破理论，固体中的应力波理论，固体强度理论，岩石动力学等，内容十分广泛[4-6]。而且爆破实际是一个相当复杂的变化过程，由于其高温、高压、时间极短等条件因素，且由于具体监测手段的限制，基本上使得人们难以开展进行具体、详细而全面的实地实时爆破过程的监测[7-9]。而且，由于爆炸实验多为破坏性实验，很难进行原型试验[10-12]。随着计算机的发展，有限单元法和有限差分法等数值方法是处理这类问题的一种有效方法，能够提供大量结构动力信息，和全部过程的变形与内力变化。

因此本文利用ANSYS/LS-DYNA有限元软件，对不同爆破结构爆破后的内部应力、应变等具体的变化规律以及爆炸后所生成的地震波的具体传播规律进行研究，为提高等离子爆破新技术的爆破效率、增强爆破效果奠定基础。

1 数值模拟

ANSYS/LS-DYNA是世界上最著名的通用显式非线性动力分析程序，能够模拟真实世界的各种复杂几何非线性(大位移、大转动和大应变)、材料非线性(140多种材料动态模型)和接触非线性(50多种)问题，特别适合求解爆炸冲击荷载或高速碰撞作用下材料和结构的动态响应分析。因此，本文应用ANSYS/LS-DYNA程序对岩石的爆破过程进行数值模拟研究。

1.1 有限元模型的建立

为简化计算区域，提高计算效率，采用流固耦合方法进行模拟一个爆炸孔爆炸全过程，爆破孔位置如图1所示。因为边界条件对爆破孔周围压力的影响很小，因此本文采用单个爆破孔进行模拟，爆破孔直径为60 mm。为节省计算时间，建立1/4模型，总尺寸为岩体直径为2 m，岩体长度为5 m，爆破孔长度为1 m。

图1 爆破孔设计Fig.1 Blast hole design

由于岩石的密度、结构组成、波阻抗、坚硬程度等物理特性对岩石中的爆炸产生极大的影响，因此岩石中的爆炸相对于在空气和水中的爆炸更复杂。在进行数值模拟研究时，考虑过多因素又会使研究无法进行，因此，在尽量满足研究要求的情况下，进行如下假定：把岩石宏观上当做连续、均匀及各向同性的介质，且不考虑实际岩石存在的缝隙节理对其产生的影响[13-15]；不考虑爆生物质的渗流作用；又因为实际岩体为无限大的，所以在计算模型中，设置了2个无反射边界(non-reflection)进行模拟，从而消除人为边界处的反射波对结构动力响应的影响。为节省计算时间，这里采用1/4模型进行数值模拟，所以需设置2个对称边界。

1.2 材料参数及算法

在ANSYS/LS-DYNA中，对于追求较为真实的结果，选择一个合适的材料模型是十分有必要的。因此必须根据材料的实际特性，选择恰当的模型来模拟，而且这个材料模型还不能跟之前已经定好的单元类型冲突。近年来，关于爆破这一非线性的动力问题研究，想要得到具有可靠性的本构曲线，由试验、归纳的方法得到，应该是比较具有可行性的。前面强调过，选择合适的材料模型是非常关键的，LS-DYNA的前处理器PREP7中就提供了Material Modeling这一子模块，以供用户进行材料具体属性的自定义。而具体的爆炸过程所适用的材料模型也可以由实验总结得出[16-18]。

岩石为花岗岩，按弹塑性材料考虑，在模型中岩体采用各向同性双线性弹塑性模型(*MAT_PLASTIC_KINEMATIC)，该模型是一种各向同性、随动硬化或各向同性和随动硬化混合模型，采用理想塑性或双线性曲线来近似材料响应，适用于梁、壳与实体模型，可以用于金属、塑料、岩石及复合材料等[19-20]。花岗岩的主要参数见表1。

表1 岩石的材料参数Table 1 Material parameters of rock

在模型中爆破模拟采用软件提供的爆破物本构(*MAT_HIGH_EXPLOSIVE_BURN)，用SOLID164实体单元进行网格划分，其材料参数如表2所示。这里采用JWL状态方程(*EOS_JWL)来模拟爆炸过程中压力与比容的关系[20-22]：

式中：A、B、R1、R2、ω——材料参数；P——压力；V——相对体积；E0——初始比内能。

表2 爆炸物的材料参数Table 2 Material parameters of explosives

网格划分时采用SOLID164实体单元进行划分，此方法划分后的模型共有9492个节点，定义了3个PART。PART1为岩体结构，PART2为爆炸物，PART3为爆炸物流动的ALE空间(*MAT_HIGH_EXPLOSIVE_BURN)。PART2和PART3间利用公共节点连接，PART1与PART2、PART3间则通过关键字设置耦合连接[13,18,23]。模型建立完成后，当炮孔孔径为0.06 m，岩体直径为2 m，岩体长度为5 m，爆破孔长度为1 m时，爆破前的模型如图2所示。

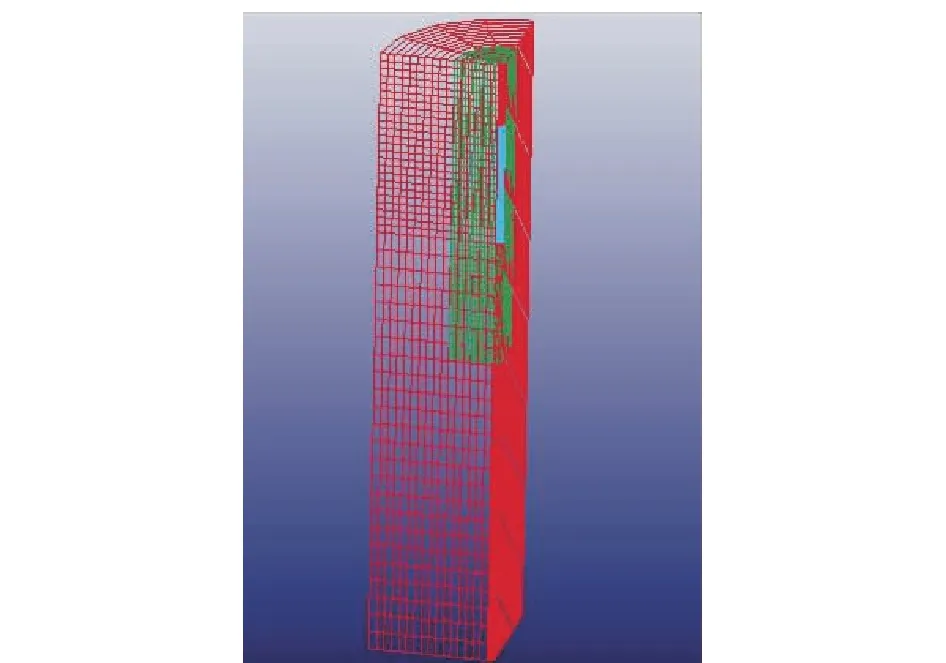
图2 爆破前的模型示意图Fig.2 Schematic diagram of the model before blasting

1.3 模拟参数

在岩石爆破中，主要影响因素包括孔径、孔深、孔距、排距等[13]。由于本文采用单孔进行模拟，所以本次模拟主要对孔径和孔深2个参数进行模拟。具体模拟参数见表3。

表3 模型尺寸参数Table 3 Model size parameters

2 数值模拟结果及验证

2.1 孔径大小对爆破作用的影响

对模拟结果进行处理，可以得到在爆炸后的不同时间、3种孔径模型的Mises等效应力云图，分别如图3～5所示。Mises等效应力代表了爆破时周围岩体中的应力发展过程[24]。

图3 0.06 m孔径Fig.3 Aperture size of 0.06m

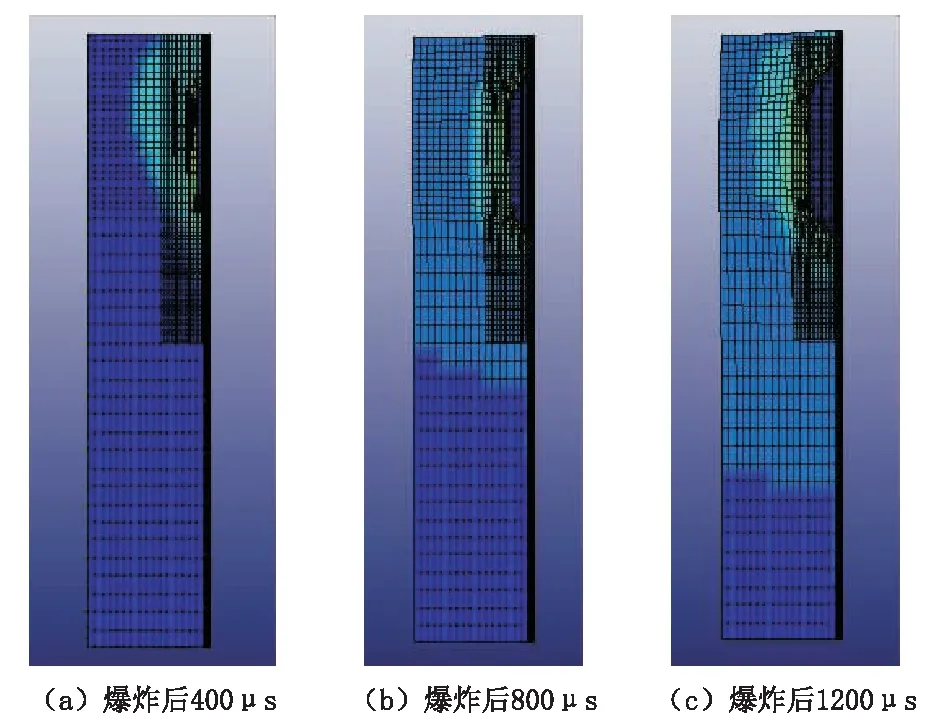
图4 0.10 m孔径炮孔Fig.4 Apertrue size of 0.10m

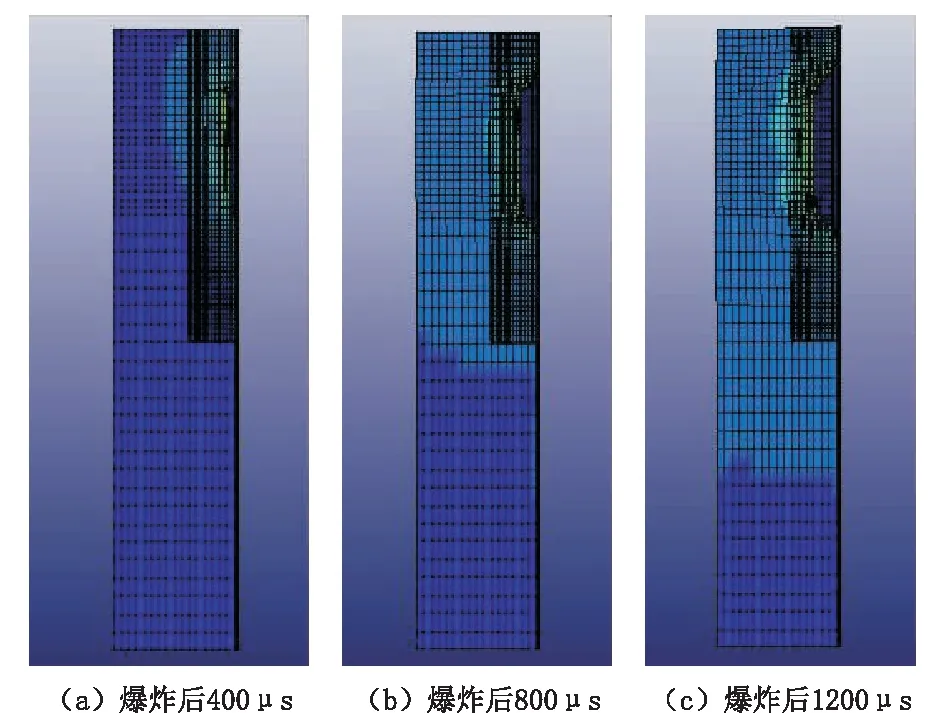
图5 0.14 m孔径Fig.5 Aperture size of 0.14m

对图中的Mises等效应力云图进行比较，可以发现爆破时，Mises等效应力呈椭圆形向周围岩体扩展。0.06 m孔径模型中的畸变能和岩体结构破坏程度最大，0.10 m孔径模型居中，0.14 m孔径模型中的畸变能和岩体结构破坏程度最小。由此可以得出，在爆破时孔径越小，积累的能量越大，对岩体破坏越大。这一点其实与爆破能量积累有关，孔径越小，单位面积积累的能量越大，爆炸产生的破坏就越大[24]。

此外，对相同时间的Mises等效应力云图的形状进行比较，可以发现不同孔径下的Mises等效应力云图形状基本相同，且都为椭圆形。由此可以得出炮孔孔径大小对云图形状没有影响，仅对破坏能力的大小产生影响。

因此，在实际进行爆破时，孔径选为0.06 m时，爆破效果最好。

2.2 孔深对爆破作用的影响

在爆破的上、下部分别取1203号、993号点，其具体位置如图6所示。分析爆炸后不同位置的爆破状态，可以得出孔深对爆破的影响。

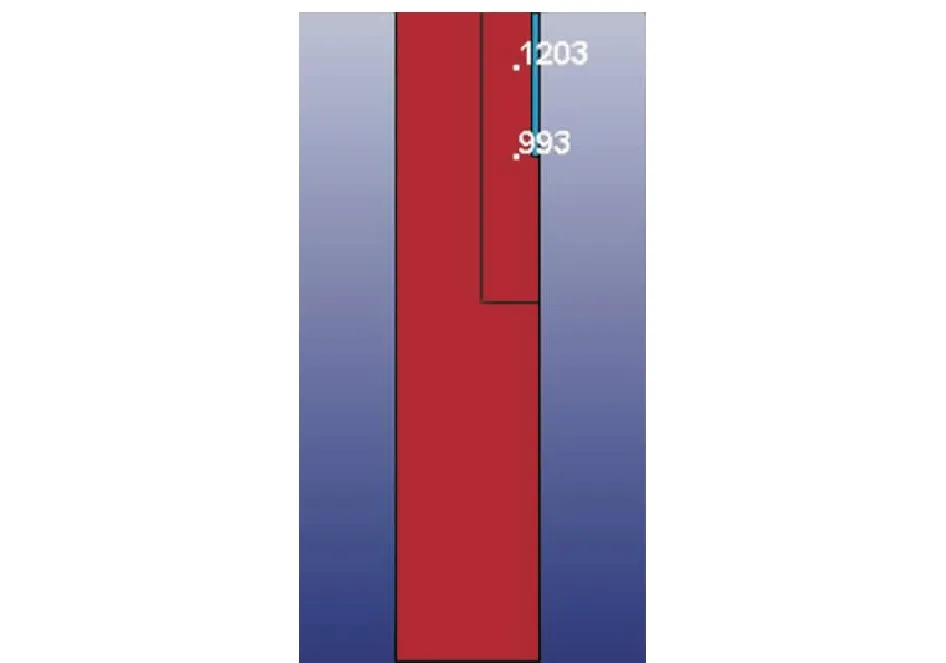
图6 爆破取样点具体位置Fig.6 Specific location of the blast sampling point

对模拟结果进行处理，得到不同孔深下3个模型在993号点上的速度和加速度变化曲线如图7、图8所示。

对模拟结果进行处理，得到不同孔深下3个模型在1203号点上的速度和加速度变化曲线如图9、图10所示。

(1)三模型的峰值和变化趋势都基本相同。

(2)不同孔深对下部岩体造成的影响小于对中部岩体的影响。

(3)对比图9和图10中的结果数据，993采样点(孔底)的响应速度和加速度明显低于1203采样点(孔中)，说明孔底是决定岩石能否破碎的关键点。从图9和图10中A、B、C三点的响应曲线来看，孔底深度在一定范围内对爆破效果的影响并不大，也就是说，在孔底能够保证破碎的前提下，可以将孔深增加，充分利用爆破能量。

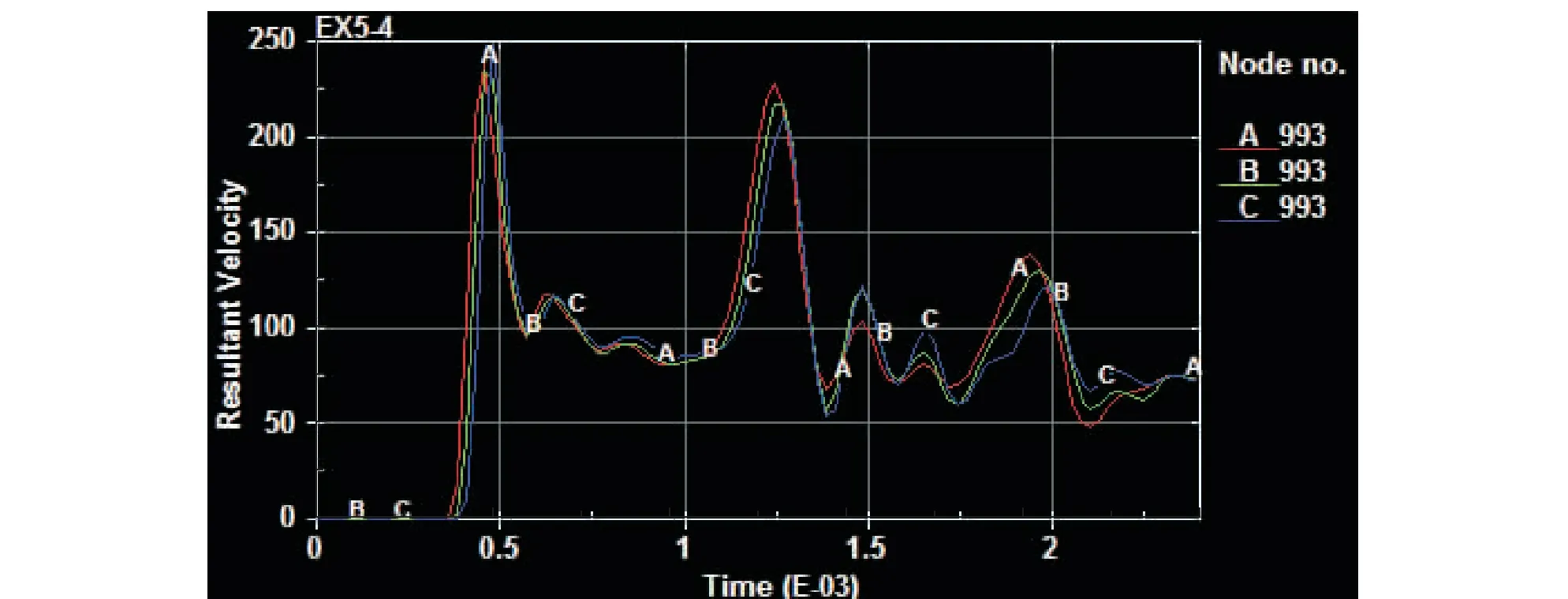
图7三模型在993号点上的速度变化曲线(A-0.3 m孔深；B-0.5 m孔深；C-0.7 m孔深)
Fig.7Speed curve of the three models at point993

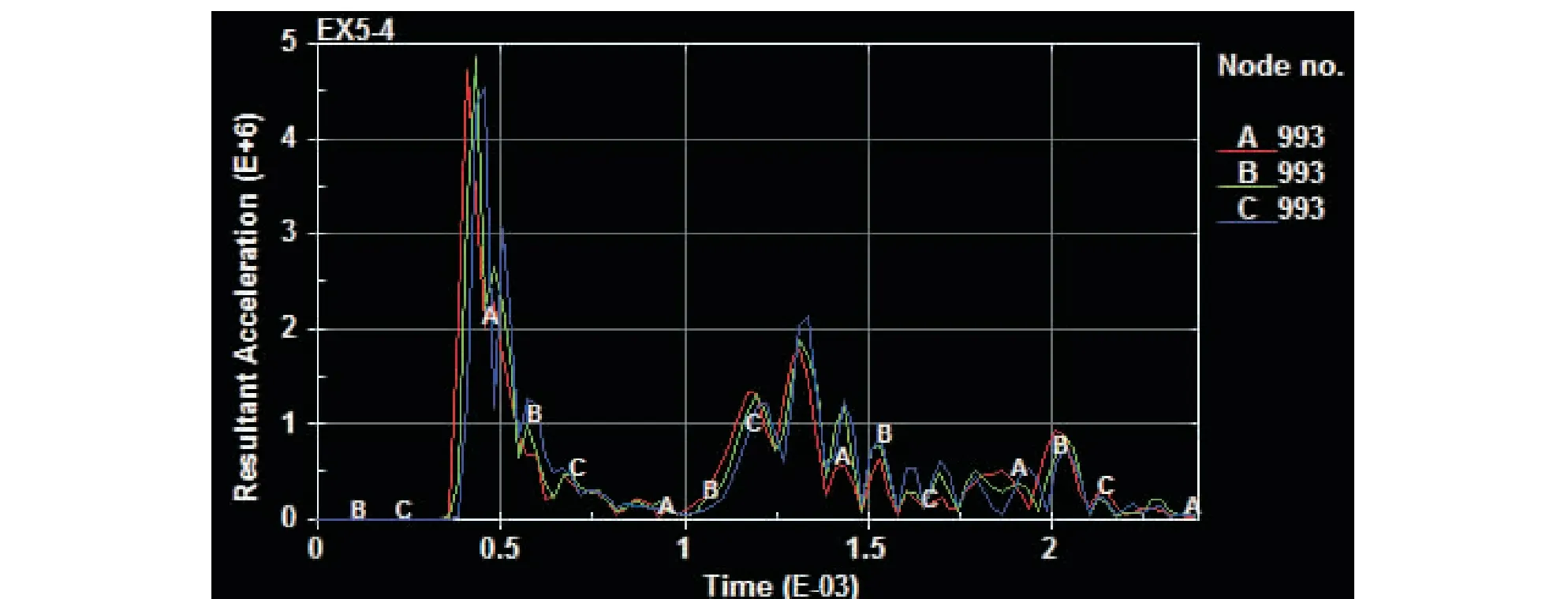
图8 三模型在993号点上的加速度变化曲线(A-0.3 m孔深；B-0.5 m孔深；C-0.7 m孔深)Fig.8 Acceleration curve of the three models at point 993

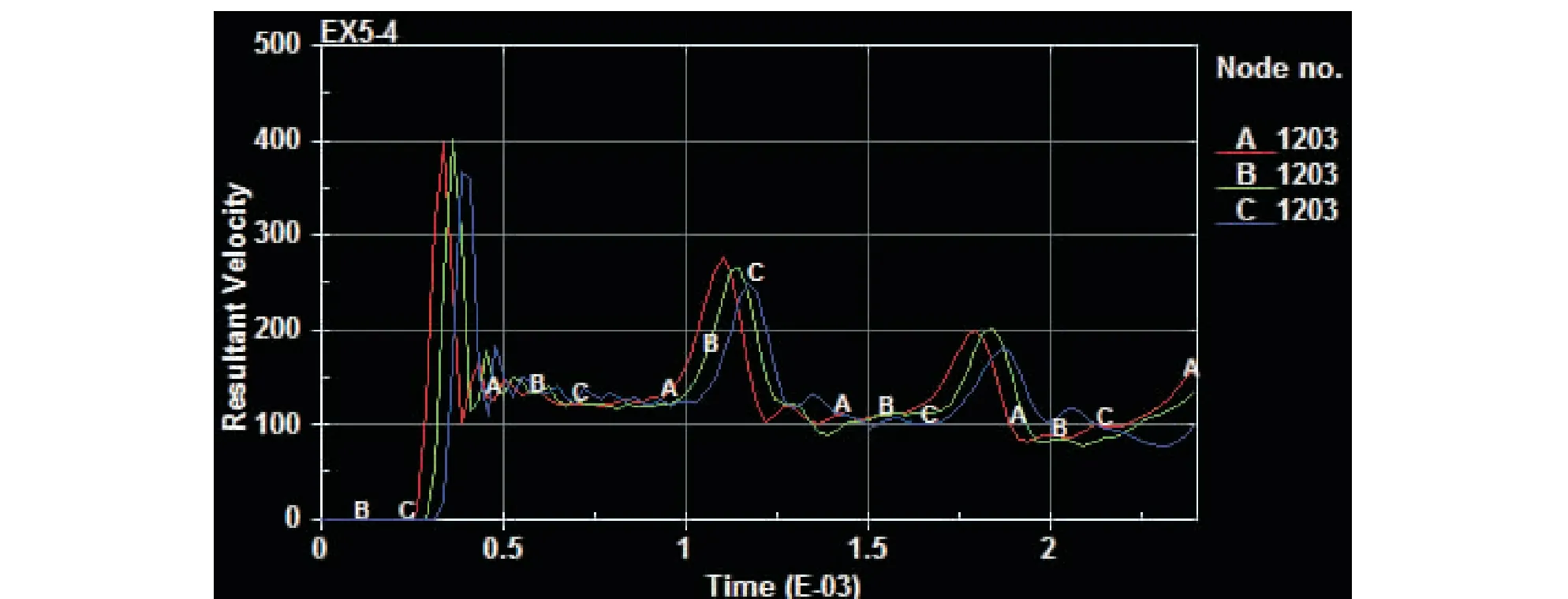
图9 三模型在1203号点上的速度变化曲线(A-0.3 m孔深；B-0.5 m孔深；C-0.7 m孔深)Fig.9 Speed curve of the three models at point 1203

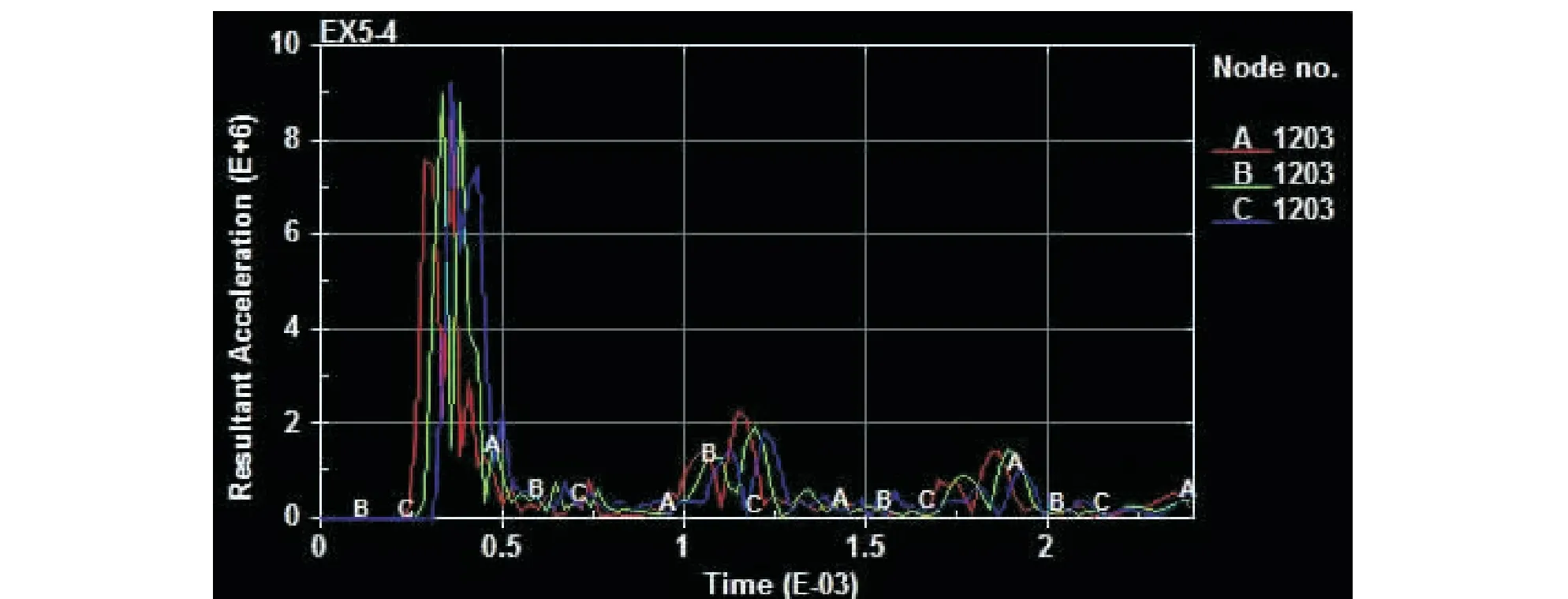
图10 三模型在1203号点上的加速度变化曲线(A-0.3 m孔深；B-0.5 m孔深；C-0.7 m孔深)Fig.10 Acceleration curve of the three models at point 1203

(4)可根据实际爆破岩石类型，结合实际工况采取相应的孔深。

(5)根据模拟结果：孔径60 mm时爆破效果最好，考虑工程使用钻孔钻头规格，将最优钻孔参数可选为孔径64 mm；当孔底深度为200 mm时，能够实现岩石屈服破坏，考虑到孔底以上岩石响应速度都大于孔底，所以孔深设定为200 mm，能够保证爆破能量的充分利用。后续可采用现场实验的方式进行验证。

由图7～10中可以看出，三模型速度和加速度曲线的峰值和变化趋势都基本相同。均为下部岩体造成的影响小于对中部岩体影响。可见岩石的破坏作用主要集中在爆破孔中部。这主要是由于爆破工具尺寸限制，爆破主要作用在爆破点处，随着深度的增大，孔底的岩石作用降低。在实际爆破过程中，孔体中部岩石的首先破裂，能量得到释放，底部岩石能量集聚效果减弱，其碎裂作用不如中部孔处岩石爆破效果。

另外，综合图7～10也可以看出，孔深长度越短，爆破对岩体造成的破坏越大。这主要是由于孔深长度越短，能量积聚空间越小，作用在孔壁的能力越大，爆破效果越好。因此，为谋求更大的爆破效率，减少钻孔时间，可根据爆破工具的实际尺寸适当选取爆破深度。

3 结论

本文通过对岩石爆破结构的数值模拟研究，结合现有实践经验分析得到以下结论：

(1)爆破时畸变能的变化自始至终都基本呈椭圆形；爆破时孔径越小，积累的能量越大，对岩体破坏越大。

(2)爆破时孔深长度越短，能量积聚空间越小，爆破对岩体造成的破坏越大；孔深长度的改变对下部岩体影响较小，对中部岩体影响较大。

等离子破岩技术具有破岩效率高，成本低，在坚硬岩石中穿凿炮孔较机械法速度快(约为机械法的3～4倍)，而成本只有机械法的一半，具有广阔的应用前景，有望成为一种简单易行，经济高效环保的新型实用破岩新工具，合理的爆破参数能极大提升等离子爆破效果，本文通过数值模拟的基础上，在满足爆破工具直径、长度要求的情况下，可以适当的减小孔径或减少孔深长度来得到更好的爆破效果。