水平定向穿越大口径管道起吊仿真分析

孙 凯， 邹 春， 付必伟

(1.中石化中原石油工程有限公司钻井一公司，河南 濮阳 457001； 2.中石化中原油田分公司濮东采油厂，河南 濮阳 457001； 3.长江大学机械工程学院，湖北 荆州 434023)

0 引言

大口径管道水平定向穿越工程中，管道安全回拖是管道铺设工程成功的标志。在管道回拖前需要控制管道的入土角度，保证管道入土角度与井眼倾角一致[1-12]。如果管道轴线与井眼轴线之间存在很大的夹角，当管道入土时就会与套管发生刮擦、瘪管等情况，造成管壁磨损，甚至是变形等事故，同时管道的回拖阻力也会急剧增大，造成管道回拖失败，进而带来巨大的经济损失[13-17]。如图1所示，在吊装作业中如果吊点设置位置不当，容易导致管道在起吊点处的应力集中，造成管道发生塑性变形。因此，在管道回拖前，必须分析吊点位置对吊装作业过程中管道力学性能的影响，设计适合的吊点位置保证管道安全进入井眼。

1 有限元模型

1.1 模型简化

图2为当管道起吊使管道前段轴线与套管轴线保持一致时的管道起吊示意图。此时管道前段长为L1，吊点1和吊点2之间的管道长为L2；吊点1的高度为H1，吊点2的高度为H2；管道入土角为β；管道支撑点处至管道前段的管道长度为L。施工过程表明吊点位置对管道起吊过程中的力学特性有很大的影响，为此研究这些吊点位置对管道起吊过程中的力学性能影响，可设计合理的起吊参数，对于管道安全回拖具有重要的意义。

由管道起吊施工工艺可知，管道在起吊过程中的受力主要包括：管道自身重力；A点对管道的支撑力；吊点1和吊点2对管道的拉力F1和F2；钻杆对管道到产生的拉力T。起吊过程中由于管道足够长在后段重力作用下，管道悬空长度一定，始终会存在一点与支撑体接触，令此临界点为A点[18]。分析中假设L足够大，使管道在起吊过程中A点始终与支撑体接触，此时A点处的挠度及起吊引起的转角为零，为此可将其简化为悬臂梁模型。

图2管道起吊示意图
Fig.2Diagram of pipeline lifting

起吊过程中由于管道足够长在后段重力作用下，管道悬空长度一定，不可能全部脱离支撑点，则始终会存在一点与支撑体接触，分析中令该点为O点。并且后文中对管道起吊进行模拟仿真验证，由此在材料力学的基础上将管道起吊模型简化为如图3所示的受力模型。为便于分析将管道分为AB、BC、CD三段，由挠度线性叠加原理可知，管道前端挠度及转角主要受2个方面的影响：(1)重力作用引起管道变形；(2)集中载荷引起管道变形。

图3 管道起吊受力分析Fig.3 Force analysis of pipeline lifting

1.2 有限元仿真模型

管道起吊作业就是通过调节两吊点的位置以及管道前段的拉力大小，使入土段管道轴线与套管轴线的夹角尽可能小，防止管道与套管或钻孔孔壁发生碰撞或瘪管事故。同时在起吊作业过程中使管道应力尽可能小，不能超过管道能承受的屈服极限应力值，保证管道安全回拖。吊点1和吊点2的位置是相互关联的，即当吊点1位置确定后，吊点2与吊点1之间存在一个最佳间距与高度差保证管道能安全起吊达到理想入土状态。图4为建立的管道起吊有限元模型，分析中采用了横梁吊具替代两个独立的吊点。因为吊具起吊也能保证吊点对管道的作用力始终竖直向上与两个独立吊点作用效果一样，因此得到合理的吊具长度就可以得到两个吊点之间的合理间距，并且在分析中吊具能根据受力状态调节两个吊点的高度，因此利用横梁吊具代替独立的吊点是合理的。

图4 管道起吊有限元计算模型Fig.4 Finite element model for pipeline lifting

1.3 材料参数设置

管道材料为X80，管道规格为Ø1016 mm×30 mm，材料参数设置如表1和表2所示。

表1 弹性阶段材料参数Table 1 Material parameters at the elastic stage

表2 塑性阶段材料应力-应变数据Table 2 Material stress-strain data at plastic stage

1.4 边界条件设置

如图5所示为模型约束条件和边界条件设置情况，根据前面的理论分析将支撑体与管道末端采用固定约束，管道本身施加均布重力载荷。分析步Step-1中吊具与参考点RP采用完全耦合约束，并施加竖直向上的微小位移载荷，使吊点与管道接触；分析步Step-2中固定RP-1，给管道前端RP-2施加竖直向下的位移载荷h=Ltanβ，保证管道前端轴线与水平线之间夹角的大小与入土角一致。

图5 管道起吊约束条件及边界条件Fig.5 Restraint conditions and boundary conditions for pipeline lifting

2 管道起吊力学仿真分析

2.1 吊点参数对管道应力分布规律影响

如图6所示，管道长度为120 m时管道起吊应力分布云图。从图中可以看出管道左端应力基本无变化，因此左端产生的应力可以看成只受管道重力作用，而管道起吊对管道左端应力影响基本可以忽略不计，这与前文中的理论分析结果一致。图中还可以看出管道应力在吊点1处比较集中，吊点1的高度也明显高于吊点2。该计算结果与文献[10]中的理论分析结果一致，因此使用该有限元模型进行起吊过程中的管道力学分析结果可信。

图6 管道应力分布云图Fig.6 Stress distribution of the pipeline

图7为不同入土角度下，管道起吊应力分布云图。从图7(a)中可以看到吊点1是管道应力集中最明显的位置，与(b)(c)(d)对比可以看出随着入土角的增大应力集中区域逐渐向吊点2扩散。管道与吊点之间的接触应力随入土角的增大而增大，并且当入土角>14°后管道出现弯曲屈服现象。因此，当管道前端为10 m时，入土角度最好不超过14°。

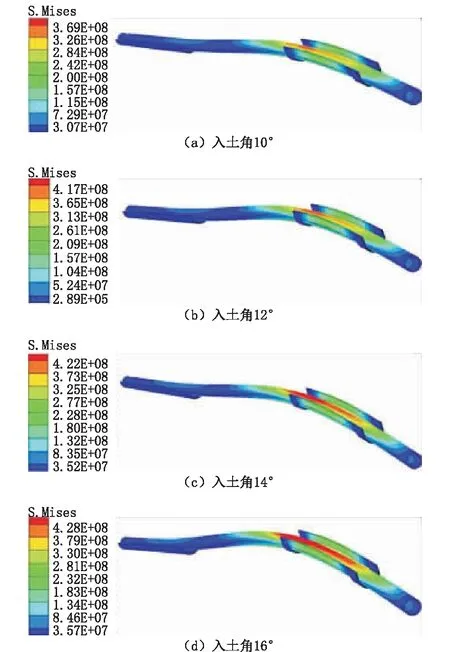
图7 不同入土角度下管道应力分布云图Fig.7 Stress distribution of pipelines at different entry angles

图8是相同吊点间距，入土角度为10°，吊点2与管道前端间距不同时的管道应力分布情况。从图(a)中可以看出管道应力在吊点1处应力集中现象最严重。由(a)(b)(c)(d)(e)5幅图中显示吊点2离管头的距离L1越大，管道应力集中现象越明显，并且管道应力集中区域分布在吊点1和吊点2之间。由管道最大应力值变化可以得到，当吊点2与管头的距离<15 m后应力降低幅度增大。进一步分析计算发现当管道前端长度L1≤8 m后，在相同条件下，起吊过程中管道会产生滑移现象。所以当入土角为10°时，吊点2的最佳位置L1为10～15 m。

图8 吊点2与管头间距不同时管道应力分布云图Fig.8 Stress distribution of pipelines at different spacings between lifting point 2 and the pipe head

图9是入土角β为10°，L1=10 m时，不同吊点间距下管道应力分布云图。图(a)～(j)显示随着吊点间距增加，两个吊点间的管道最大集中用力逐渐减小。当两吊点之间的间距L2>26 m，管道与吊点的接触应力逐渐增大。因此，当吊点2位置确定后，两个吊点之间的距离存在最佳的范围保证管道能安全起吊。通过分析发现入土角β为10°，L1=10 m时，吊点间距的最佳范围为22～26 m。

2.2 管道前端长度对其应力分布的影响

图10是管道最大应力随吊点间距增大的变化曲线。从图中可以看出随着吊点间距增大，管道起吊产生的最大应力逐渐减小，在L2≤20 m时吊点间距对管道应力影响较小；L2>20 m时随吊点间距的增大，管道最大应力降幅增大，随着吊点间距的继续增大，管道应力又趋于平稳并在L2>26 m时出现应力反弹现象。并且5种情况管道最大应力变化规律基本相似，图中可以直观看出入土角β=10°时，吊点间距L2的合理范围为22～26 m，在L1=10 m时管道最大应力明显要小于其余4种情况。所以当入土角β=10°时，吊点间距合理范围为22～26 m，吊点距管头长度L1=10 m。

由于上面分析中，吊点2距管道间距为20 m和25 m的两种情况，管道最大应力随吊点间距增大持续减小，为此还需进一步加大吊点间距，分析它对管道最大应力的影响，从而获得最佳的吊点间距。计算结果如图11所示，图中显示当L2≥30 m后管道最大应力值出现回升现象，所以这两种情况下吊点间距的合理范围为26～30 m。

图12为不同L1下吊点高度差与吊点间距之间的关系曲线。从曲线上可以看出高度差随吊点间距的增大而增大，并且基本表现为线性关系。管端长度为10 m时两吊点之间的高度差明显要小于其余4组。

2.3 吊点间距对管道应力分布的影响

图13～15是入土角度为12°、14°和16°时，管道最大应力随管道前端长度L1增大的变化情况。图中显示入土角相同的情况下，管道最大应力随L1增大而增大，吊点间距从22 m到24 m的过程中，管道最大应力明显降低。图中还可以看出管道前端长度L1超过10 m后，管道应力快速增大，因此管道前端长度设置为10 m较为合理。

2.4 入土角对管道应力分布的影响

图16、图17、图18是不同入土角情况下，管道最大应力与L1的关系曲线。图16中显示除了入土角度为10°，吊点间距为22 m时起吊应力未超过管道的许可应力外，其他情况下管道的起吊应力均超过了管道的屈服极限，而随着吊点间距的增加其他3种情况的最大应力也逐渐减小。所以不同入土角度对应的合理吊点位置不同，因此还需进一步对不同入土角下的合理吊点间距确定进行分析。

图9不同吊点距离下管道应力分布云图
Fig.9Stress distribution of pipeline at different distances between the lifting points

图10 管道最大应力变化曲线Fig.10 Maximum stress curve of the pipeline

为了便于施工过程中吊点位置的定位，对不同入土角度合理吊点位置的确定进行了研究，计算结果如表3所示。结果显示入土角度为12°和14°时，以管道应力未超过屈服极限为标准，得到对应的合理吊点间距分别为28～36、30～36 m。并且入土角度>14°后管道起吊很容易造成管道损坏，建议入土角度最好不超过14°。

图11 管道最大应力变化曲线Fig.11 Maximum stress curve of the pipeline

图12 吊点高度差与吊点间距关系曲线Fig.12 Lifting point height vs lifting point spacing curve

图13 入土角为12°Fig.13 Entry angle at 12 degrees

图14 入土角为14°Fig.14 Entry angle at 14 degrees

图15 入土角度为16°Fig.15 Entry angle at 16 degrees

3 结论

综上所述，对吊点位置优化的分析计算可以得到如下结论：

图16 吊点间距22 mFig.16 Spacing of the lifting points at 22m

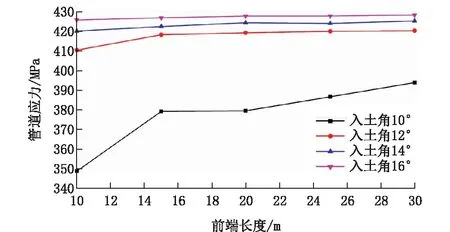
图17 吊点间距24 mFig.17 Spacing of the lifting points at 24m

图18 吊点间距26 mFig.18 Spacing of the lifting points at 26m

表3 管道最大应力值MPa

当吊点位置确定后管道应力随入土角度的增大而增加；入土角一定时，管道应力随吊点2与管头距离L1的增大而增大；入土角、吊点2与管头距离一定时，随吊点间距增大，管道应力先减小后增大。

通过对不同入土角度，吊点位置对Ø1016 mm×30 mm的管道应力计算分析得到：管端长度为10 m，入土角为10°时，两吊点的许用间距22～26 m；入土角为12°时，两吊点的许用间距28～36 m；入土角为14°时，两吊点的许用间距30～36 m；入土角为16°时，管道应力基本超出了管道的屈服应力，建议管道入土角度最好不超过16°。