SAS软件实现Serfling回归模型

宁波市疾病预防控制中心(315010)

李 宁 张 良 纪 威 韩航涛 樊明锁 俞延峰

【提 要】 目的 为方便研究人员使用Serfling回归模型做疾病负担研究，开发SAS宏程序用于相关数据整理、模型应用和结果展示。方法 以宁波市2015年1月1日到2018年12月31日0～3岁儿童流感和肺炎(ICD-10：J09～J18)门诊数据为实例，介绍和验证SAS宏程序%SERFLING(IN_DSN=,AGE=,SEX=,CLIP=,WEEKS_EPI=)。结果 按照SAS宏程序%SERFLING的参数说明，在指定输入数据集(IN_DSN=)基础上按需选择年龄范围(AGE=)、性别(SEX =)、是否将不足一周的头尾数据删除(CLIP =)以及是否使用传统Serfling回归模型(WEEKS_EPI =)，就可以自动完成对原始数据的整理、Serfling回归模型应用和相关结果展示。结论 SAS宏程序%SERFLING方便了Serfling回归模型的应用，具有一定的实用性。

1963年Serfling博士首次提出Serfling回归模型，并且用于肺炎和流感导致的超额死亡研究[1]，之后该模型被广泛应用于各类季节性传染病导致的超额发病率、住院率和死亡率等研究[2-4]。2015年Xiaoli Wang等提出调整Serfling回归模型，该模型通过迭代方式自动排除大于阈值的按周统计数，解决了人为判断疾病流行期的困难，而且使拟合效果更好[4]。

Serfling回归模型的基本思想简单明了，但在文献中尚未查到相应SAS程序。本研究设计了名为%SERFLING的SAS宏程序，用于Serfling回归模型的数据整理、模型应用和结果展示。该SAS宏程序只需指定输入数据集(IN_DSN=)以及可选的几个参数如年龄范围(AGE=)、性别(SEX=)、流行期(WEEKS_EPI=)等，就可自动完成对传统或调整Serfling回归模型的应用，提高了工作效率。

资料与方法

1.资料

通过宁波市区域卫生信息平台，收集57家医疗机构2015年1月1日至2018年12月31日0～3岁儿童的流感和肺炎门诊数据(ICD-10：J09～J18)共计243202例，收集字段包括门诊时间(DATE)、性别(SEX)和年龄(AGE)，如表1所示。

表1 数据集TEST部分观测

2.方法

Serfling回归方程如下：

Yt=a+bt+ct2+dt3+fsin(2πt/52)+gcos(2πt/52)+hsin(4πt/52)+icos(4πt/52)+et

其中Yt代表第t周统计数，t代表连续的周次(t=1,2,3,…)，a代表截距；b、c、d、f、g、h、i为回归系数，其中a+bt+ct2+dt3反映长期趋势，fsin(2πt/52)+gcos(2πt/52)+hsin(4πt/52)+icos(4πt/52)反映季节周期性；et是误差项。模型的拟合优度通过决定系数R2判断。

传统Serfling回归模型需要人为删除流行期对应统计数来拟合基线[1-2]。调整Serfling回归模型通过计算机迭代来排除流行期数据，第一次迭代先用全部按周统计数拟合Serfling回归模型，从全部按周统计数中删除大于拟合值的数据，第二次迭代用上一次迭代保留的按周统计数拟合Serfling回归模型，重新从全部按周统计数中删除大于拟合值95%可信区间上限的按周统计数，第三次迭代用上一次迭代保留的按周统计数拟合Serfling回归模型，重新从全部按周统计数中删除大于拟合值95%可信区间上限的按周统计数，不断重复直到R2下降，取R2最大的Serfling回归模型来拟合基线[5-6]。

3.程序

/*SAS宏程序%SERFLING，参数说明见表2*/

%MACRO SERFLING(IN_DSN=,AGE=,SEX=,CLIP=,WEEKS_EPI=);

/*数据集IN_DSN按DATE排序*/

PROC SORT DATA=&IN_DSN OUT=TEMP_1SELECT;

BY DATE;RUN;

/*如果指定AGE=，则筛选相应年龄范围*/

/*如果未指定AGE=，则直接跳转%SKIP_AGE:*/

%IF"&AGE"=""%THEN%GOTO SKIP_AGE;

DATA _NULL_;/*提取参数AGE=相关信息*/

IF FIND("&AGE",′-′)THEN DO;

AGE_LOWER=INPUT(SCAN("&AGE",1,′-′),BEST.);

AGE_UPPER=INPUT(SCAN("&AGE",2,′-′),BEST.);

END;ELSE DO;

AGE_LOWER=&AGE;AGE_UPPER=&AGE;END;

CALL SYMPUT(′AGE_LOWER′,AGE_LOWER);

CALL SYMPUT(′AGE_UPPER′,AGE_UPPER);RUN;

DATA TEMP_1SELECT;/*筛选相应年龄范围*/

SET TEMP_1SELECT;

WHERE &AGE_LOWER<=AGE<=&AGE_UPPER;RUN;

%SKIP_AGE:

/*如果指定SEX=，则筛选相应性别*/

/*如果未指定SEX=，则直接跳转%SKIP_SEX:*/

%IF "&SEX"=""%THEN %GOTO SKIP_SEX;

DATA _NULL_;/*提取参数SEX=相关信息*/

IF 0 THEN SET TEMP_1SELECT;

SEX_VTYPE=VTYPE(SEX);

CALL SYMPUT(′SEX_VTYPE′,SEX_VTYPE);RUN;

DATA TEMP_1SELECT;/*筛选相应性别*/

SET TEMP_1SELECT;WHERE

%IF &SEX_VTYPE=N %THEN SEX=&SEX;

%ELSE SEX="&SEX";RUN;

%SKIP_SEX:

/*对数据按周汇总整理*/

PROC TIMESERIES DATA=TEMP_1SELECT OUT=TEMP_2WEEK;

ID DATE INTERVAL=WEEK ACCUMULATE=TOTAL;

VAR COUNT;RUN;

/*如果指定CLIP=YES，则根据实际修剪头尾*/

%IF"&CLIP"=""%THEN %GOTO SKIP_CLIP;

PROC SQL NOPRINT;

SELECT MAX(DATE),MIN(DATE)

INTO:DATE_MAX,:DATE_MIN

FROM &IN_DSN;QUIT;

DATA TEMP_2WEEK;/*根据实际修剪头尾*/

SET TEMP_2WEEK END=LAST;

IF _N_=1 AND DATE^=&DATE_MIN THEN DELETE;

IF LAST AND DATE^=&DATE_MAX-6 THEN DELETE;RUN;

%SKIP_CLIP:

/*为SERFLING回归方程生成新变量*/

DATA TEMP_3SERFLING;SET TEMP_2WEEK;

WEEK=WEEK(DATE);/*用于传统SERFLING回归模型*/

COUNT_EXCLUDE=COUNT;

T=_N_;/*生成连续周次*/

T_B=T;T_C=T*T;T_D=T*T*T;

T_F=SIN(2*CONSTANT(′PI′)*T/52);

T_G=COS(2*CONSTANT(′PI′)*T/52);

T_H=SIN(4*CONSTANT(′PI′)*T/52);

T_I=COS(4*CONSTANT(′PI′)*T/52);RUN;

/*如果未指定WEEKS_EPI=，则使用调整SERFLING回归模型*/

/*如果指定WEEKS_EPI=，则直接跳转%SKIP_ADJUST:，使用传统SERFLING回归模型*/

%IF"&WEEKS_EPI"^=""%THEN %GOTO SKIP_ADJUST;

/*第一次迭代*/

PROC REG DATA=TEMP_3SERFLING PLOTS=NONE OUTEST=TEMP_4FITSTAT RSQUARE;/*输出R2*/

MODEL COUNT_EXCLUDE=T_B T_C T_D T_F T_G T_H T_I / SELECTION=MAXR;

OUTPUT OUT=TEMP_6PREDICTED PREDICTED=PREDICTED;/*输出拟合值*/

RUN;QUIT;

DATA _NULL_;SET TEMP_4FITSTAT;

CALL SYMPUT(′R2′,_RSQ_);RUN;

DATA TEMP_6PREDICTED;SET TEMP_6PREDICTED;

THRESHOLD=PREDICTED;RUN;/*阈值*/

/*第N次迭代*/

%NEXT_SERFLING:

DATA TEMP_6PREDICTED_NEW(DROP=PREDICTED:UCL:LCL:);

SET TEMP_6PREDICTED;COUNT_EXCLUDE=COUNT;

IF COUNT>THRESHOLD THEN CALL MISSING(COUNT_EXCLUDE);RUN;

ODS OUTPUT SELPARMEST=TEMP_5PARM_NEW;

PROC REG DATA=TEMP_6PREDICTED_NEW PLOTS=NONE OUTEST=TEMP_4FITSTAT_NEW RSQUARE;

MODEL COUNT_EXCLUDE=T_B T_C T_D T_F T_G T_H T_I / SELECTION=MAXR;

OUTPUT OUT=TEMP_6PREDICTED_NEW PREDICTED=PREDICTED UCL=UCL LCL=LCL;/*输出拟合值95%CI上限*/

RUN;QUIT;

ODS OUTPUT CLOSE;

DATA _NULL_;SET TEMP_4FITSTAT_NEW;

CALL SYMPUT(′R2_NEW′,_RSQ_);RUN;

%IF &R2_NEW<=&R2 %THEN %GOTO NEXT_PLOT;/*不断重复直到R2下降*/

%LET R2=&R2_NEW;

DATA TEMP_4FITSTAT;SET TEMP_4FITSTAT_NEW;RUN;

DATA TEMP_5PARM;SET TEMP_5PARM_NEW;RUN;

DATA TEMP_6PREDICTED;SET TEMP_6PREDICTED_NEW;

THRESHOLD=UCL;RUN;/*阈值*/

%GOTO NEXT_SERFLING;/*继续迭代*/

%SKIP_ADJUST:

/*使用传统SERFLING回归模型*/

DATA _NULL_;/*提取参数WEEKS_EPI=相关信息*/

FORMAT WEEKS $1000.;WEEKS=0;

DO I=1 TO COUNT("&WEEKS_EPI",′ ′)+1;

WEEK=SCAN("&WEEKS_EPI",I,′ ′);

IF FIND(WEEK,′-′)THEN DO;

WEEK_LOWER=SCAN(WEEK,1,′-′);

WEEK_UPPER=SCAN(WEEK,2,′-′);

WEEKS=CATX(′ ′,WEEKS,′OR′,WEEK_LOWER,′<=WEEK<=′,WEEK_UPPER);

END;ELSE WEEKS=CATX(′ ′,WEEKS,′OR′,′WEEK=′,WEEK);END;

CALL SYMPUT(′WEEKS′,WEEKS);RUN;

DATA TEMP_3SERFLING;SET TEMP_3SERFLING;

IF &WEEKS THEN CALL MISSING(COUNT_EXCLUDE);RUN;

ODS OUTPUT SELPARMEST=TEMP_5PARM;

PROC REG DATA=TEMP_3SERFLING PLOTS=NONE OUTEST=TEMP_4FITSTAT RSQUARE;

MODEL COUNT_EXCLUDE=T_B T_C T_D T_F T_G T_H T_I / SELECTION=MAXR;

OUTPUT OUT=TEMP_6PREDICTED PREDICTED=PREDICTED UCL=UCL LCL=LCL;

RUN;QUIT;ODS OUTPUT CLOSE;

%NEXT_PLOT:

/*删除无统计学意义的项后，重新拟合模型*/

PROC SORT DATA=TEMP_5PARM;BY DESCENDING STEP;RUN;

DATA TEMP_5PARM;SET TEMP_5PARM;RETAIN MAX_STEP;

IF _N_=1 THEN MAX_STEP=STEP;IF STEP=MAX_STEP;RUN;

DATA _NULL_;LENGTH REGRESSORS $1000;

SET TEMP_5PARM END=LAST;RETAIN REGRESSORS ′′;

IF FIND(VARIABLE,′Intercept′)THEN DO;

IF PROBF<0.05 THEN CALL SYMPUT(′INTERCEPT′,′′);

ELSE CALL SYMPUT(′INTERCEPT′,′NOINT′);END;

ELSE IF PROBF<0.05 THEN REGRESSORS=CATX(′ ′,REGRESSORS,VARIABLE);

IF LAST THEN CALL SYMPUT(′REGRESSORS′,REGRESSORS);RUN;

ODS OUTPUT FITSTATISTICS=TEMP_4FITSTAT PARAMETERESTIMATES=TEMP_5PARM;

PROC REG DATA=TEMP_6PREDICTED(DROP=PREDICTED:UCL:LCL:)PLOTS=NONE;

MODEL COUNT_EXCLUDE=®RESSORS / &INTERCEPT;

OUTPUT OUT=TEMP_6PREDICTED PREDICTED=PREDICTED UCL=UCL LCL=LCL;

RUN;QUIT;ODS OUTPUT CLOSE;

/*结果展示*/

ODS HTML IMAGE_DPI=300;ODS GRAPHICS /NOBORDER;

PROC SGPLOT DATA=TEMP_6PREDICTED;

SERIES X=DATE Y=COUNT;

SERIES X=DATE Y=PREDICTED / LINEATTRS=(PATTERN=DOT);

SERIES X=DATE Y=UCL / LINEATTRS=(PATTERN=SHORTDASH);

XAXIS GRID;YAXIS GRID;RUN;

/*删除无关数据集*/

PROC DATASETS LIB=WORK NOLIST;

DELETE TEMP_4FITSTAT_NEW TEMP_5PARM_NEW TEMP_6PREDICTED_NEW;RUN;QUIT;

/*超额病例数*/

DATA TEMP_6PREDICTED;SET TEMP_6PREDICTED;

IF COUNT>UCL THEN EPI=1;RUN;

DATA TEMP_6PREDICTED;SET TEMP_6PREDICTED;

BY EPI NOTSORTED;

IF FIRST.EPI AND LAST.EPI THEN CALL MISSING(EPI);

IF EPI=1 THEN DO;EXCESS=COUNT-PREDICTED;

LCL_EXCESS=COUNT-UCL;UCL_EXCESS=COUNT-LCL;END;RUN;

/*汇总SERFLING回归模型拟合结果*/

DATA TEMP_6PREDICTED;SET TEMP_6PREDICTED;

IF EPI=1 THEN COUNT_EPI=COUNT;

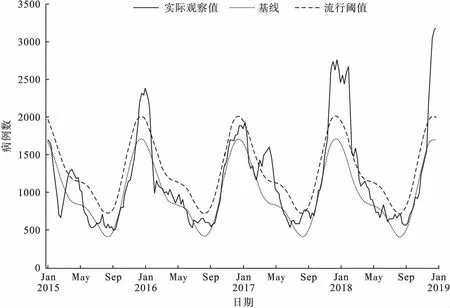
IF MDY(7,1,2015)<=DATE

ELSE IF DATE

ELSE IF DATE

PROC SQL;CREATE TABLE TEMP_7SUMMARY AS

SELECT YEAR,SUM(EPI)AS EPI_WEEKS,

SUM(EXCESS)AS EXCESS,SUM(LCL_EXCESS)AS LCL,SUM(UCL_EXCESS)AS UCL,

SUM(EXCESS)/SUM(COUNT_EPI)AS EXCESS_EPI,

SUM(LCL_EXCESS)/SUM(COUNT_EPI)AS LCL_EPI,

SUM(UCL_EXCESS)/SUM(COUNT_EPI)AS UCL_EPI,

SUM(EXCESS)/SUM(COUNT)AS EXCESS_ALL,

SUM(LCL_EXCESS)/SUM(COUNT)AS LCL_ALL,

SUM(UCL_EXCESS)/SUM(COUNT)AS UCL_ALL

FROM TEMP_6PREDICTED

GROUP BY YEAR;RUN;QUIT;

%MEND SERFLING;

表2 宏程序%SERFLING参数说明

结 果

对以上代码进行编译后就可以根据表2参数说明调用SAS宏程序%SERFLING，例如：%SERFLING(IN_DSN=TEST,AGE=0-3,CLIP=YES)。WORK逻辑库依次生成7个临时数据集：TEMP_1SELECT、TEMP_2WEEK、TEMP_3SERFLING、TEMP_4FITSTAT、TEMP_5PARM和TEMP_6PREDICTED、TEMP_7SUMMARY。

原始数据集TEST(表1)包含4个变量：日期变量DATE、性别变量SEX、年龄变量AGE、计数变量COUNT，由于是个案形式，所有COUNT=1；数据集TEMP_1SELECT根据参数AGE=0-3，完成对原始数据集TEST的筛选，保留0～3岁儿童观测；数据集TEMP_2WEEK在数据集TEMP_1SELECT基础上对COUNT变量按周汇总，并且删除监测不足一周的头尾数据(CLIP=YES)；数据集TEMP_3SERFLING根据Serfling回归方程Yt=a+bt+ct2+dt3+fsin(2πt/52)+gcos(2πt/52)+hsin(4πt/52)+icos(4πt/52)+et构建第一次迭代所需数据，变量COUNT_EXCLUDE即方程中的Yt，变量T为连续周次即方程中的t，T_B、T_C、T_D、T_F、T_G、T_H、T_I分别表示方程中的t、t2、t3、sin(2πt/52)、cos(2πt/52)、sin(4πt/52)、cos(4πt/52)，变量WEEK表示根据变量DATE计算的当年周次(用于传统Serfling回归模型)；数据集TEMP_4FITSTAT记录了最终的R2值；数据集TEMP_5PARM(表3)记录了Serfling回归模型最终的参数估计；数据集TEMP_6PREDICTED(表4)根据最终的Serfling回归模型计算拟合值(PREDICTED)、拟合值的95%可信区间上限(UCL)以及在此基础上判断的流行周(EPI，定义为连续2周以上实际按周统计数超过拟合值的95%可信区间上限，即COUNT>UCL)、超额数(EXCESS，定义为流行周期间实际数与拟合值的差值，即EXCESS=COUNT-PREDICTED)；图1以线图方式直观展示实际观察值、基线和流行阈值，其中实线表示实际按周统计数(COUNT)，点线表示拟合值(PREDICTED)，短虚线表示拟合值的95%可信区间上限(UCL)；数据集TEMP_7SUMMARY(表5)在数据集TEMP_6PREDICTED基础上，根据自定义的流行年度(YEAR，例如将每年7月至次年6月作为一个监测年度)汇总流行周数(EPI_WEEKS)、超额数(EXCESS)及其95%可信区间(LCL、UCL)、超额数占流行周观察总数比例(EXCESS_EPI)及其95%可信区间(LCL_EPI、UCL_EPI)、超额数占全年度观察总数比例(EXCESS_ALL)及其95%可信区间(LCL_ALL、UCL_ALL)，经过简单整理后可得表6。

表3 % SERFLING输出结果：数据集TEMP_5PARM部分变量和观测

结合图1和表6可以发现，2017/2018年度流感和肺炎流行周中，0～3岁儿童超额就诊病例数及其占全年度观察病例数比例与往年相比有明显上升，且流行持续17周，高于前两个监测年度，提示可能出现病原变化，需高度关注。

表4 %SERFLING输出结果：数据集TEMP_6PREDICTED部分变量和观测

*：变量COUNT_EXCLUDE中的“-”表明该周病例数(COUNT)未用于最后的Serfling回归方程；变量EPI中的“-”表明该周最终被判断为非流行周。

图1 %SERFLING输出结果：实际观察值、基线和流行阈值

年度EPI_WEEKSEXCESSLCLUCLEXCESS_EPILCL_EPIUCL_EPIEXCESS_ALLLCL_ALLUCL_ALL55767 4248 7285 0.4062 0.2992 0.5132 0.1810 0.1333 0.2287 2015/201663677 1855 5498 0.2700 0.1362 0.4038 0.0662 0.0334 0.0989 2016/2017136415 2452 10378 0.3571 0.1365 0.5778 0.0744 0.0284 0.1203 2017/20181713297 8136 18458 0.3649 0.2233 0.5065 0.1955 0.1196 0.2713

表6 2014-2015至2017-2018年度宁波市0～3岁儿童流感和肺炎超额病例

讨 论

Serfling回归模型常用于流感的季节性和疾病负担研究[2-3,7]，评估流感的季节性流行或大流行对人群健康的影响，对流感防控具有重要指导意义。近年来该模型也用于其他病毒性疾病的研究[6]，可为病毒研究和疾病防控提供依据。鉴于目前无Serfling回归模型程序实现的相关文献，本文设计了名为%SERFLING的SAS宏程序，集数据整理、模型应用和结果展示于一体，方便了Serfling回归模型的使用，也提高了工作效率，具有一定的实用性。