LKNNI:一种局部K近邻插补算法*

杨日东 李 琳 陈秋源 周 毅△

【提 要】 目的 针对K近邻插补法在缺失率较大的数据集上的性能不佳，提出一种局部K近邻插补法。方法 在6个完整的公开数据集上按照不同缺失率随机删除数据，根据填充数据和原始数据计算算法的填充性能，将局部K近邻插补法与K近邻插补法、多重插补法对比。结果 局部K近邻插补法在缺失率较低的条件下，填充性能与多重插补法接近，且略胜于K近邻插补法。在缺失率较高的条件下，局部K近邻插补法的性能明显优于K近邻插补法，且略胜于多重插补法。结论 相比K近邻插补法，局部K近邻插补法非常适合处理缺失率较大的数据集。

随着信息时代的发展，各个领域积累了大量数据，如何有效地利用这些数据，已成为目前一大研究热点。然而，实际中往往会出现数据缺失、噪声、重复和不一致等情况，这很大程度地影响了数据挖掘算法的稳定[1]。因此，对缺失数据集进行处理就显得十分重要。数据重复和数据的不一致均可进行算法筛查，而造成数据缺失可能是由于数据无法获取或者在操作过程中被遗漏，在不进行缺失值处理的情况下，某些机器学习算法甚至无法直接使用。因此，缺失值填充是数据挖掘和机器学习领域中一个实际且有挑战性的问题[2]。

相关研究

K近邻插补(Knearest neighbor imputation，KNNI)是Olga Troyanskaya[3]提出的一种基于数据局部相似性的填充算法。KNNI的基本思想是，对于含缺失值的样本，其缺失的数据可参考与它最类似的K个样本。具体地说，KNNI将数据集划分为两个集合，一个集合包含所有的完全样本(即不含缺失值的样本)，另外一个集合包含所有的不完全样本(即存在缺失值的样本)。对于每个不完全样本，求其在完全样本集中的K近邻，对于缺失值是分类属性的，则填充K近邻样本该属性值的众数；对于缺失值是数值属性的，则填充K近邻样本该属性值的平均数。由于不完全样本的缺失值是根据“相邻”样本求得，因此KNNI算法不会增加过多的新样本信息。

尽管 KNNI 是一种优秀的填充算法，但是KNNI 的填充效果极大程度地受缺失率的影响。KNNI算法在数据集缺失率较大时，数据集中的完全样本非常少，这意味着，对于不完全样本而言，在完全样本中算出的K近邻样本此时可能并非真正意义上的“近邻”。这就会导致缺失样本填充时参考的K近邻实际上与样本本身还有一定的差距，最终导致填充的数值误差较大。另外，当缺失率大到一定程度时，数据集中并不一定含有完全数据，此时，将无法运用传统的KNNI进行缺失值填充。

传统插补算法属于单值插补，填充值是唯一的，无法体现缺失数据的不确定性，一定程度改变了样本分布。为了弥补单值插补的缺陷，综合考虑缺失值的不确定性，Rubin[4]等人提出多重插补法(multiple imputation，MI)。多重插补方法产生多个候选插补值，形成了多个完整的数据集，这些可能的估计值反映了数据的不确定性，综合分析得到估计量，进行统计推断。构造若干个可能估计值实际上是模拟一定条件下的估计值分布，借估计值分布来估计缺失变量的实际后验分布[5]。文献[6]对比了多重插补法与均值插补、EM算法和回归插补等在不同缺失率下的填充性能，结果表明，在缺失率高的条件下多重插补法比其他方法的性能更佳。因此，本文将多重插补法与局部K近邻插补法(localK-nearest neighbor imputation，LKNNI)进行对比。

局部K近邻插补法

考虑到KNNI在缺失率较大时难以找到真正的“近邻”样本，本文提出了一种局部K近邻插补法。算法的初衷是通过切片，使得填充不完全样本时的参考样本(即用于求K近邻的样本集)更多，从而提高填充准确度。所谓切片，是指数据集在特定属性集合上的投影。例如：对于属性集{年龄,婚姻,学历,家庭条件}、数据集T={(“青年”,“未婚”,“本科”,“良好”),(“中年”,“已婚”,“硕士”,“一般”)}，则T在婚姻和学历属性上的投影为T′={(“未婚”,“本科”),(“已婚”,“硕士”)}。

对不完全样本Ti的第j个缺失属性进行缺失值填充时，数据T中的样本只需满足其本身在Ti中未缺失的属性也不缺失(因为计算K近邻时需要)并且在Ti当前的缺失属性j也不缺失(因为计算填充值时需要)，即可将此样本加入求Ti的K近邻的样本集合当中，无论此样本是否是完全样本。这样一来，填充所参考的样本集由不完全样本Ti决定，并非必须参考完全样本，相比传统KNNI灵活。算法的具体步骤如下：

LKNNI算法：

输入：含缺失数据的数据集T，K近邻的参数K

输出：已填充数据集

根据数据集T中样本的缺失值个数，对样本进行倒序排序

对于T中的每个样本Ti，求Ti的所有缺失属性。

对于Ti的每个缺失属性j：

(1)切片：遍历T，求出T中满足以下所有条件的样本slice_data：

①样本Ti中未缺失的属性在slice_data中也不缺失

②样本Ti当前的缺失属性j在slice_data中也不缺失

(2)求样本Ti在slice_data中的K近邻TiK

(3)若当前样本的缺失属性j是分类属性，将TiK在属性j的取值的众数填充到Ti的缺失属性中

(4)若当前样本的缺失属性j是数值属性，将TiK在属性j的取值的平均数填充到Ti的缺失属性中

输出数据集T

在上述LKNNI算法中，步骤1的目的是为了降低参考样本集为空的风险，即利用“贪心算法”的思想，对T中样本按照缺失值个数进行倒序排序，认为样本的缺失值个数越多，其切片得到的数据集也越大，空集的可能更小。

LKNNI算法与KNNI算法最大的区别在于：KNNI算法填充不完全样本是根据完全样本中的K近邻，而LKNNI算法是根据样本当前正在处理的缺失属性和未缺失属性，在整个数据集T中进行一次投影，然后在投影得到的数据集中求得当前样本的K近邻，最后进行相应的填充。与KNNI算法相比，LKNNI算法使得不完全样本可在一个更大的样本集中求得K近邻，这意味着K近邻算法可学习的样本数更大，找到的近邻“更像”当前处理的不完全样本。

实 验

1． 数据集

如表1所示，本次实验采用4个来自UCI上的公开数据集。

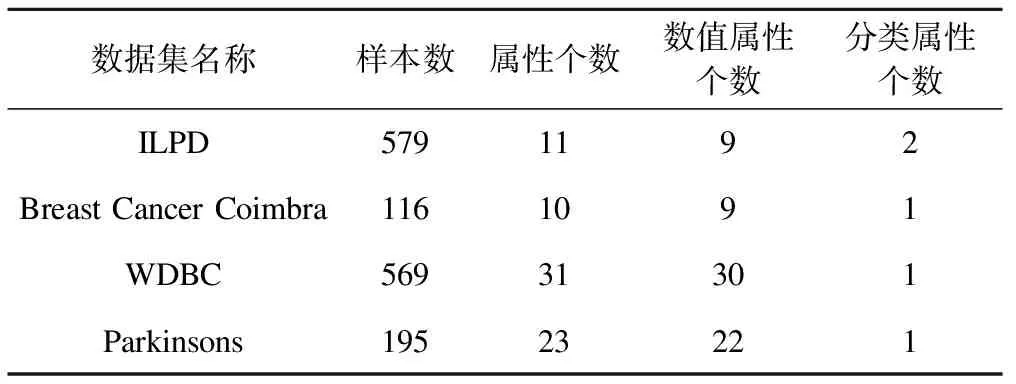
表1 数据集统计描述

2.实验设计

(1)模拟缺失：为了衡量填充值与实际数值之间的相似度，我们按照文献[9]中的做法，采用完整数据集，然后采用随机删除的方法模拟多变量随机缺失，经过缺失值填充后再对比填充值与原始属性值。

(2)归一化：为了保证求解K近邻时不受数值属性的量纲影响，本实验在预处理时，均对所有的数值属性进行归一化处理。具体计算方式如下：

其中xi表示未归一化之前的值，xmin表示该属性的最小值，xmax表示该属性的最大值。

(3)度量指标：为了准确评价填充算法在不同数据集上的性能，本实验在计算度量指标时，均对所有的数值属性进行归一化处理。在衡量算法性能时，数值属性的填充效果用均方误差表示；分类属性则采用正确率表示[8-9]。计算方式如下：

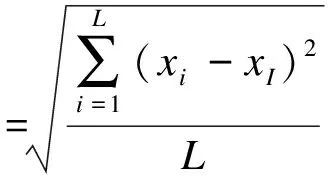
其中，L是缺失个数，xi是原始数据，xI是填充的数据。

3.实验结果

考虑到KNNI在缺失率大时无法运行的局限性，我们根据不同数据集上KNNI所能够运行的最大缺失率来设计缺失率的取值区间。并且为了保证实验结果可信度，降低模拟缺失带来的误差，本实验对相同填充算法和相同缺失率的样本进行30次实验，用度量指标的平均值作为实验结果。如图1～4所示。

从图1～4可以看出，三种算法的填充性能均随缺失率的增大而变差，且KNNI对缺失率最为敏感，MI次之，而LKNNI最不敏感。可以得出结论：由于LKNNI在缺失率较大时，通过投影得到的数据集远大于完全样本集，因此找到的K近邻样本更接近于待插补的不完全样本，从而填充性能更佳，适合处理缺失率大的数据集。

图1 不同算法、缺失率在ILPD数据集上的填充性能比较

图2 不同算法、缺失率在Breast Cancer Coimbra数据集上的填充性能比较

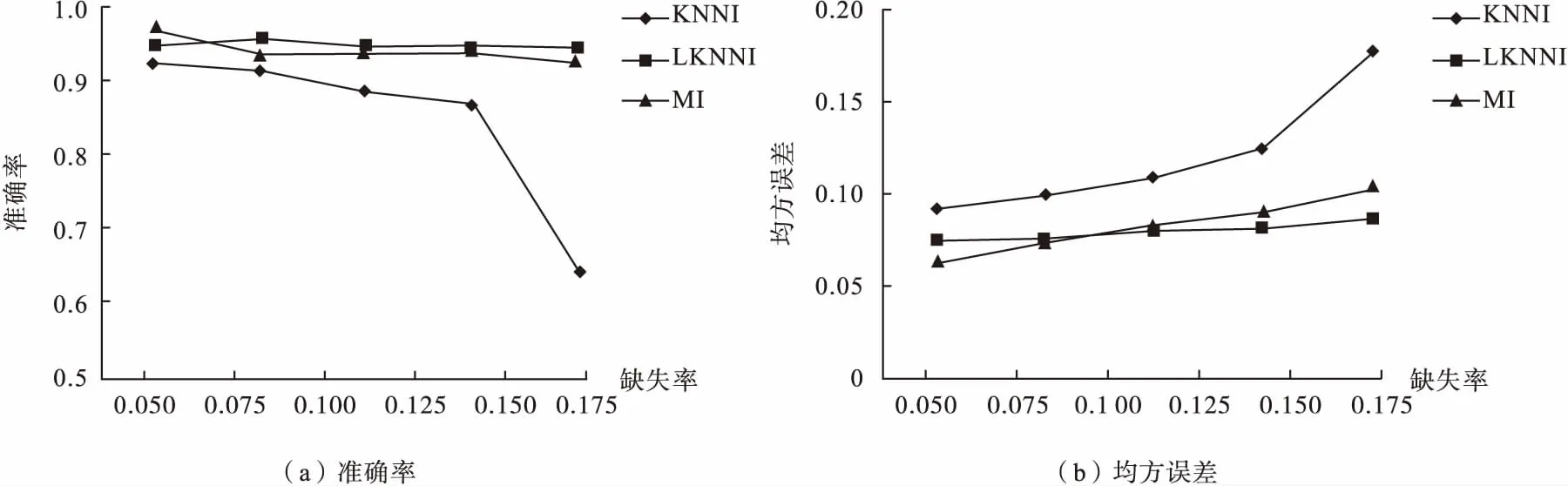
图3 不同算法、缺失率在WDBC数据集上的填充性能比较

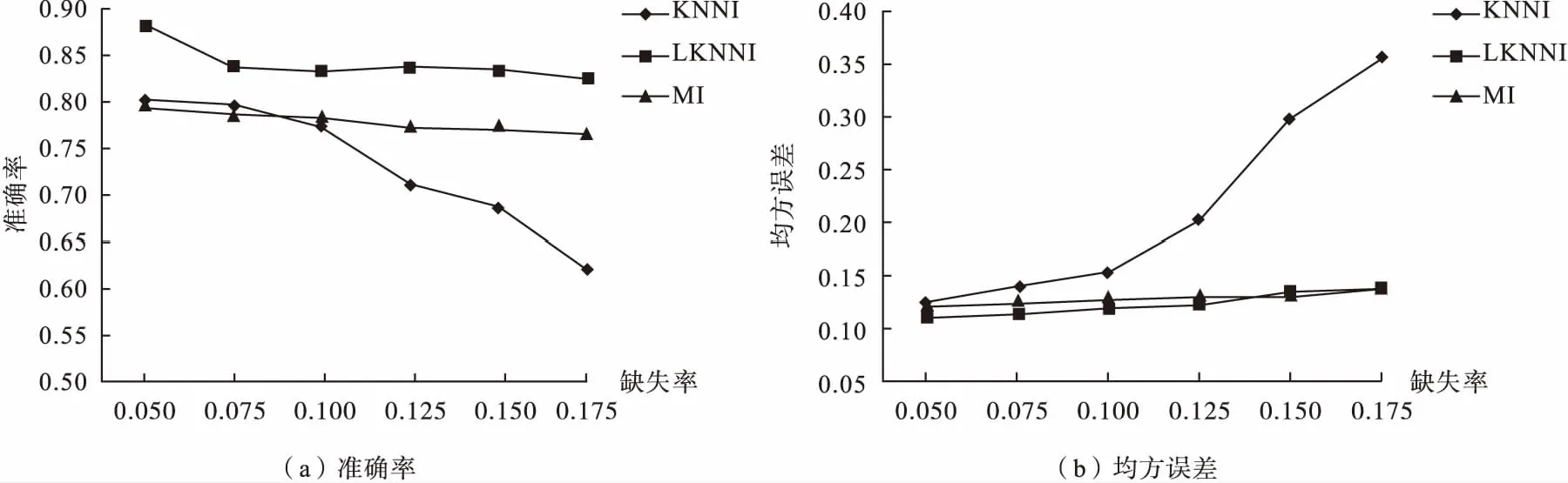
图4 题不同算法、缺失率在Parkinsons数据集上的填充性能比较

另外，不同的数据集，基于K近邻思想的插补方法与多重插补法的性能比较结果不同。例如：WDBC数据集本身易于分类，适合多重插补等模型，而ILPD数据集本身可能更适合K近邻模型，因此不能简单地认为哪种算法的性能绝对优于其他算法。但是，在缺失率较大时，LKNNI的填充效果通常优于KNNI。

总 结

本文提出一种基于K近邻插补法改进的算法——局部K近邻插补法，是在KNNI的基础上，引入切片思想，扩大不完全样本寻找K近邻的集合容量，从而易于找到与不完全样本更类似的样本。通过4个UCI数据集，在不同缺失率下进行对比实验。结果表明，LKNNI在缺失率小的条件下性能与MI接近且略优于KNNI；LKNNI在缺失率大时明显优于KNNI，且略胜于MI。

LKNNI在填充不完全样本时，每填充一个缺失值均在全局数据上进行投影，以求得该不完全样本的可参考样本。而传统KNNI则一次性求出参考样本(即完全样本)，因此LKNNI相比传统KNNI速度更慢。我们发现，在同一不完全样本中，当前缺失值的参考样本必定是前一个缺失值的参考样本的子集。因此，在未来研究中，在一个不完全样本的填充过程中，将不再以全局数据进行投影，而是在前一个缺失值的参考样本集进行投影，以此减小数据规模，进而提高LKNNI的整体运行速度。