丢包在线补偿伺服电机NCS神经网络滑模控制

陈 莹 唐友亮 张 锦 於 锋

1(宿迁学院机电工程学院 江苏 宿迁 223800)2(南通大学电气工程学院 江苏 南通 226019)

0 引 言

直流伺服电机由于其结构简单，且能够保证平滑的调速性能以及精确的定位性能，在工业领域得到了广泛的应用[1]。随着网络技术的不断发展，直流伺服电机网络控制系统的研究也得到了广泛的关注。将传统的直流伺服电机控制理论与网络控制系统的相结合，使得系统结构简化，成本降低，灵活性增强。但是，网络控制系统也存在一些无法避免的问题，比如网络时延、数据丢包或者数据包乱序等[2]。针对网络时延与数据丢包问题，许多文章通过支持向量机对时延丢包进行预测补偿，取得了较好的效果[3]。但是，核函数构造对最后的支持向量机预测精度会产生较大影响，目前常用的构造方法均通过经验法或者试凑法进行组合构造，上述方法均存在一定的性能保守性[4-5]。

滑模变结构控制由于其出色的鲁棒性在非线性控制领域得到了广泛的应用。文献[6]提出了一种积分型滑模变结构控制器，利用负载转矩观测器抑制了负载扰动的影响。文献[7]提出了一种互补滑模变结构的控制方法，将互补滑模面与广义滑模面相结合，得到了较好的控制效果。文献[8]将变指数趋近律应用于滑模变结构控制，在一定程度上可以有效减弱系统抖振。但是上述研究均只考虑如何降低抖振，没有综合考虑滑模控制的整体性能优化，且研究对象均不存在丢包与时延的影响。

考虑到直流伺服电机网络控制系统的非线性特性，为了进一步解决网络传输给控制系统带来的不利影响，本文提出了一种滑动时窗与优化多核LS-SVM相结合的丢包在线预测补偿多包传输直流伺服电机网络控制系统神经网络PID趋近律滑模控制方法。

1 时延多包传输NCS建模

设直流伺服电机NCS传感器和执行机构采用时钟驱动方式，控制器采用事件驱动方式，数据带有时间戳并多包传输，且无时序错乱。根据文献[9]合并控制时延τca和输出时延τsc为τ(k)。在此基础上，建立离散系统模型，表示为:

(1)

式中：x′(k)∈Rn为系统状态变量，u′(k)∈Rm为控制量输入，A′、B′、C′为适维系数矩阵。设τ(k)为时变但有界的Markov随机变量，τ(k)的状态空间取为Ω={0,1,2}，系统的时延状态迁移关系为:

(2)

定义∏=πij,(i,j∈Ω)为系统的时延状态迁移矩阵。由于直流伺服电机网络控制系统式(1)中显含时延项τ(k)，这对于滑模面的设计来讲是非常困难的。因此，基于预测控制思想[10]，通过线性变换，将原系统转换为无时延系统。定义线性变换：

(3)

将式(3)代入式(1)，原系统等价为:

x(k+1)=Ax(k)+Bu(k)

(4)

由文献[11]可知，式(4)表示的系统为状态完全能控系统。

图1 丢包补偿器多包传输NCS结构

(5)

(6)

式中：σ(k)为LS-SVM补偿值与系统状态真实值的预测误差系数。

在系统进行数据传输时，若发生丢包，则未更新的数据由补偿器进行补偿更新，综上所述，可得丢包补偿的时延直流伺服电机NCS模型为：

(7)

2 滑动时窗多核LS-SVM在线补偿

最小二乘支持向量机较好地解决了传统SVM学习算法中回归计算量随样本数目膨胀的难题[12]。给定样本序列(x1,y1)，(x2,y2)，…，(xi,yi)，…，(xl,yl)，假设xi∈Rn代表输入向量，yi∈R代表输出向量，则最小二乘支持向量机求解问题可以表述为：

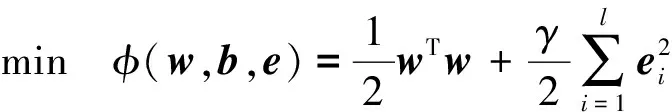
(8)

式中：φ(·)代表从n维向量空间到nh维向量空间的映射函数；w∈Rnh表示权值系数，ei∈R代表误差向量，b∈R表示偏置系数；γ>0代表惩罚因子，从式(8)可知惩罚因子对预测误差有着极大的影响。根据LS-SVM相关理论可得基本方程为：

(9)

根据SVM的原理可知核函数的选取对最后的回归预测有重大影响。核函数在针对确定的特征空间和对应映射，可以大幅度减少计算复杂性。常见的三种核函数形式主要为：

(1) 多项式核函数：

Kp(x,y)=[λ(xTy)+c]d

(10)

(2) Sigmoid核函数：

Ks(x,y)=tanh(ηxTy+k2)

(11)

(3) 高斯核函数：

(12)

式中:x、y代表输入空间向量，λ、c、d、η、σ为核函数的参数。除上述三种常用的核函数外，还有多二次曲面核函数、正交多项式展开核和傅里叶展开核以及各种改进核函数等。为便于说明，本文以上述常用的三种核函数为例进行说明。

已知核函数满足如下性质[14]：

(1) 假设K1和K2均为核函数，α1和α2均为正实数，则K=α1K1+α2K2也是核函数；

(2) 假设K1和K2均为核函数，则K=K1·K2也是核函数；

(3) 假设K1为核函数，则K=exp(K1)也是核函数。

根据上述三条性质，可以得到无数个不同的核函数，其组合关系如图2所示。

图2 核函数组合示意图

(13)

式中：Ki为利用上述三条性质的单个核函数任意排列组合得到的新核函数。ωi表示各个组合核函数的权重系数。该多核函数综合了各种核函数的特点，且通过权值系数大小调整不同核函数对预测精度的影响大小，从而将核函数的选择问题转换为核函数权值的优化求解问题，提升支持向量机的精度。相应的目标函数为：

(14)

(15)

对式(9)求解，即可得到系数α和b，定义特征矩阵Q=Ω+γ-1I，则：

(16)

为实现在线丢包补偿，本文利用滑动时窗策略结合LS-SVM进行在线预测建模。

滑动时窗策略如图3所示，时窗每移动一次更新训练数据，假设时窗的长度为L，该长度数值的大小的与样本个数的大小有关。

图3 滑动时窗策略示意图

具体的滑动时窗在线网络控制系统丢包补偿LS-SVM算法更新步骤可以参考文献[13]。

3 神经网络滑模控制器设计

3.1 PID趋近律分析

定理若给定PID趋近律表达式为：

(17)

式中：l>0代表比例系数；m>0是积分系数；n>0表示微分系数；t0代表系统初次到达滑模面时间；t代表当前时刻。设计离散滑模控制滑模面为：

(18)

式中：F滑模面常数矩阵。

则该PID趋近律滑满足动模态存在和到达条件，且该滑模控制器渐进稳定，可以计算得到控制量u(k)。

证明：

当s>0且s→0+时，存在以下条件：

(19)

同理，当s<0且s→0-时，存在以下条件：

(20)

根据上述分析，提出的PID趋近律满足滑动模态存在和到达条件。

由于在系统未到达滑模面时，积分项的作用为0，当s(t)=0时，对式(20)求解可得系统第一次到达滑模面的时间为：

(21)

由式(21)可知，到达时间t0是有限值。

根据对直流伺服电机网络控制系统补偿建模可知相应的状态空间模型如式(7)所示，假设状态变量个数为2，设计离散滑模控制滑模面为：

(22)

式(6)等价于：

(23)

(24)

已知第一次到达滑模面时满足如下条件：

s(k0)=0,k0≠0

(25)

则联立式(23)和式(24)可得：

(26)

确定k之后，则可解得滑模面常数矩阵F为：

F=diag[z11]

(27)

[s(k+1)-s(k)]s(k)<0

(28)

但由文献[14]可知，式(28)只是离散准滑模运动存在的必要条件，而非充分条件。针对该问题，Sarpturk提出一种离散滑模到达充分条件，表示为:

|s(k+1)|<|s(k)|

(29)

根据连续趋近律分析可得离散滑模面函数，表示为：

(30)

通过式(30)可知，此时无论s(k)>0或者s(k)≤0，均满足式(29)的要求。进一步分析该PID趋近律滑模控制器的稳定性，定义Lyapunov函数为：

V(k)=s2(k)

(31)

可得:

ΔV(k)=s2(k+1)-s2(k)

(32)

由于满足式(31),所以ΔV(k)<0，因此可以证明该滑模控制器渐进稳定。此时可以计算出相应的控制量u(k)。

3.2 神经网络PID趋近律

PID趋近律能否实现保证控制速度的情况下保持较小抖振取决于比例、积分和微分三个参数的选择。为实现高效滑模控制，三个参数应该随到达滑模面的时间而自适应的调整。因此，考虑到神经网络强大的非线性映射能力[15]，提出了一种基于神经网络的PID趋近律参数在线调整滑模控制器。

神经网络的输入量为滑模切换函数s(k)和及其变化量Δs(k)，其中Δs(k)=s(k+1)-s(k)，这两个输入量能够反映此时与滑模面的状态以及未来的运动趋势，输出量为PID趋近律的三个参数l、m、n，径向基神经网络属于多层前向神经网络，具备较强的非线性映射能力[16-18]。

本文应用的是广义网络RBF,结构图如图4所示。

图4 广义RBF网络结构

具体的广义RBF非线性映射计算根据文献[19]方法进行，在此不作赘述。

4 仿真验证

定义直流伺服电机网络控制系统的采样周期为0.1 s,根据文献[2]可知当负载电流为0时，状态空间模型参数矩阵为：

定义时延状态转移矩阵为：

(33)

图5为对应∏1的时延分布。

图5 时延分布图

为减少计算量，相应的子核函数个数n=6，其组成如表1所示。

表1 核函数组成

利用未丢包的数据包进行训练，通过文献[19]的混沌自适应人工鱼群优化方法对多核LS-SVM的核函数参数以及结构参数进行优化，相应地设人工鱼条数NUM=30，最大迭代次数Iterate_times=170，初始化视野Visual=15，拥挤度因子φ=0.4，觅食尝试次数Try_number=10，衰减因子α=0.4，β=0.3，阈值δ=0.5。优化结果如图6所示。

图6 优化结果

相应的各个核函数的权值优化曲线如图7所示，同理可以得到LS-SVM其他结构参数的大小。

图7 核函数权值优化结果

相应的滑模控制器参数设定初始值为比例系数l=30、积分系数m=1、微分系数n=5，设置神经网络层数为8层，隐含层的神经元个数为4，利用训练样本得到相应的权值系数，进一步由极点配置计算得滑模面常数矩阵：

F=diag[z11 1]=diag[4.27 1 1]

(34)

从而可以计算出控制量。Truetime作为网络控制系统理想的虚拟仿真工具，得到了广泛的应用。本文的仿真验证环境为MATLAB2016中的Truetime工具箱。首先对滑动时窗多核LS-SVM在线预测补偿进行验证，给定角位移传感器状态变量数据变化曲线如图8中的粗直线，分别在30%以及60%丢包率条件下利用基于滑动时窗策略的组合核函数LS-SVM[12]与优化多核LS-SVM进行丢包预测补偿，预测对比结果如图8所示。

图8 丢包预测补偿对比

从图8中的预测补偿结果可以看出，无论在丢包率为30%或者60%时，多核LS-SVM丢包预测较组合核LS-SVM的状态量更接近无丢包状态变换曲线，且当丢包率较小时，基本可以完全复现无丢包状态量变化情况。说明无论丢包率的大小，多核LS-SVM的预测补偿精度都比组合核LS-SVM高。

进一步考虑在不同丢包率条件下，在线补偿对神经网络滑模控制的影响。图9为丢包率在30%条件下无补偿神经网络滑模控制与优化多核LS-SVM在线补偿神经网络滑模控制响应对比，图10为丢包率在60%条件下无补偿神经网络滑模控制与优化多核LS-SVM在线补偿神经网络滑模控制响应对比。可以看出，无论是丢包率为30%还是60%，基于优化多核LS-SVM在线补偿神经网络滑模控制响应的快速性与稳态性能均优于无数据补偿的神经网络滑模控制，进一步证明了数据包在线预测补偿对丢包条件下的神经网络滑模控制效果有改善的效果，能够在一定丢包率条件下实现较好的控制效果。

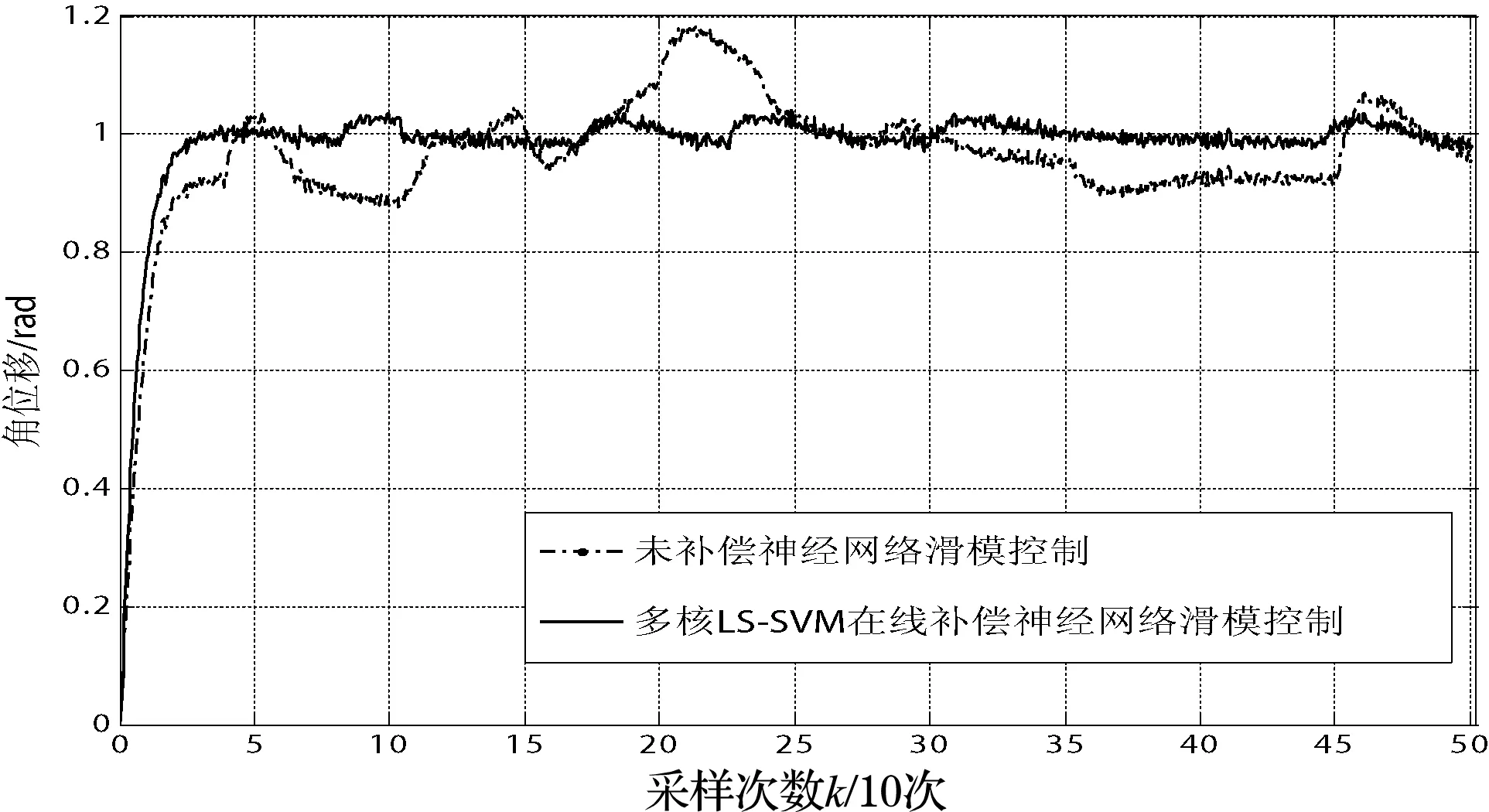
图9 30%丢包率条件下控制对比

图10 60%丢包率条件下控制对比

为验证神经网络PID趋近律滑模控制的优越性，在丢包率为20%条件下，给定参考跟踪信号为角位移等于1的阶跃信号，在滑动时窗优化多核LS-SVM在线丢包补偿条件下分别利用分段趋近律滑模控制[20]、模糊幂次趋近律滑模控制[21]以及神经网络PID趋近律滑模控制对直流伺服电机网络系统进行控制，角位移响应曲线如图11所示，相应的稳态放大图如图12所示。

图11 不同趋近律滑模控制效果对比

图12 不同趋近律滑模控制效果放大图

具体的100次采样周期之后稳态抖振结果如表2所示。

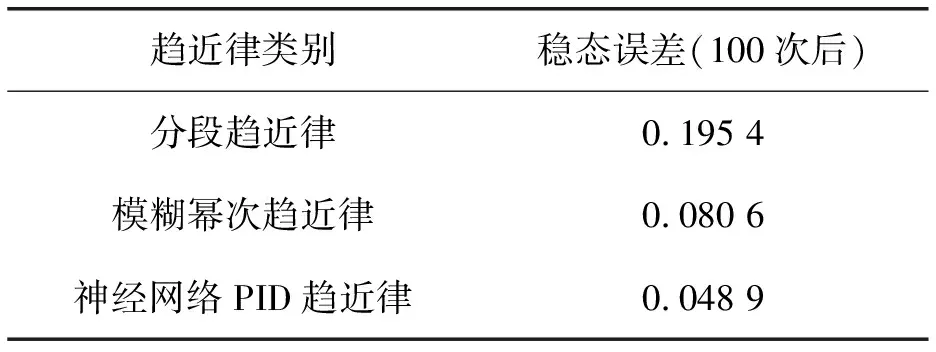
表2 稳态抖振结果对比

从上述对比结果可以看出，虽然分段趋近律的初始响应速度最快，但是其抖振幅值明显大于其他两种滑模控制方法。模糊幂次趋近律相对于分段趋近律来说，抖振大大减小，但是其响应调节时间却明显增大。神经网络PID趋近律滑模控制抖振幅值最小，响应曲线能够快速上升至目标值并且保持较小的稳态误差。

再通过控制量u(k)的响应曲线来分析不同趋近律下的抖振情况,如图13、图14所示，可以看出控制量u(k)在神经网络PID趋近律的滑模控制中抖振幅度较PID趋近律明显减小。表3为100次采样之后不同趋近律的平均稳态误差，神经网络PID趋近律的滑模控制平均稳态误差明显小于其他两种趋近律滑模控制，从稳态误差的角度进一步说明了神经网络PID趋近律的抖振较弱。

图13 不同趋近律控制量对比

图14 不同趋近律控制量放大图

趋近律类别稳态误差(100次后)分段趋近律0.028 6模糊幂次趋近律0.012 4神经网络PID趋近律0.008 4

原因分析：分段趋近律由于通过与滑模面的距离来实现两种趋近律的切换，在响应初期，主要考虑趋近速度，故其响应速度较快。但是，趋近律切换之后，主要考虑减小抖振，所以响应曲线会有明显的转折出现。但是此时状态变量还未到达滑模面，因此切换后趋近律此时并未起到减小抖振的作用，反而使得响应速度减慢。此种方法的切换时机选取对最后的控制效果会产生较大影响。模糊幂次趋近律能够在线调整趋近律速度，其设计目标主要在于减少系统抖振，增强系统对外部干扰以及参数摄动的鲁棒性，因此其鲁棒性较强，但是响应速度较慢。而神经网络PID趋近律能够通过神经网络非线性映射能力使得比例、积分和微分参数可调，在前期通过增大比例系数使得趋近速度加快，后期接近滑模面时减小比例系数，增大积分系数减小抖振振幅，减少稳态误差，同时增大微分系数抑制抖振，兼顾了响应速度与抑制抖振。

针对丢包率来说，不同的丢包率存在较大的随机性，丢包发生的频率会极大地影响SVM预测补偿的效果，同样的丢包率条件下的预测补偿效果不一样，对于本文研究的丢包补偿来说，仿真结果能够得到大概的丢包率上限。当丢包率达到40%时，系统的补偿效果开始变差，但是从控制效果来看依旧能够保持一定的跟踪能力；当丢包率达到50%以上时，系统的预测补偿效果明显变差，而且控制跟踪效果也急剧恶化。对于具体的丢包率上限，还需要进行进一步研究。

5 结 语

本文针对存在时延以及丢包的多包传输直流电机网络控制系统，提出了一种滑动时窗策略结合优化多核LS-SVM的在线丢包补偿神经网络PID趋近律滑模控制器，并通过仿真得出如下结论：

(1) 将时延转换为无时延系统，将多核支持向量回归的组合核函数构造问题转换为系数优化问题，为多核函数的构造提供了一种普遍方法，并且滑动时窗优化多核LS-SVM在线丢包补偿且能够保证较高的补偿精度，极大地降低了丢包给控制系统带来的不利影响。

(2) 神经网络PID趋近律滑模控制较分段趋近律以及模糊幂次趋近律滑模控制既能保证较快的响应速度，又使得抖振幅值小，兼顾了响应速度与抖振抑制。

(3) 基于滑动时窗多核LS-SVM在线补偿条件下的神经网络PID滑模控制能够较好地实现存在时延丢包的多包传输直流伺服电机网络控制系统的跟踪控制，且对数据丢包具备一定鲁棒性。