基于认证数据的学生上网时间特征分析
郭玉彬 吴宇航 薄傲峰 郑淑敏 张晓鹏
1(华南农业大学数学与信息学院 广东 广州 510642)2(中山大学数据科学与计算机学院 广东 广州 510006)
0 引 言
高校校园网是承载高校学生学习、生活、娱乐等各类活动的基础性设施。随着移动互联网技术的发展,学生对网络的使用增长迅速,其上网行为也呈现多样化和复杂化特征。校园网认证数据包含了学生用户名、上网端口地址、上下线时间等信息。通过对这些数据的分析,可发现学生上网时间、时长等信息及相关的特征分类规律。而这些规律性信息对学生管理、专业课程设置等工作具有较高的参考价值。2016年上网认证数据量约8 000万条,并以每年约1亿条的速度增加。
针对校园网日志数据进行学生行为分析的研究有很多,大多数研究都是采用传统的K-means算法对在线时长和校园网使用流量进行聚类,利用聚类结果分析每一类用户的上网行为和优化校园网管理[1-4]。文献[5]基于一种改进的K-means算法,即SimiClustering算法,对校园网用户在线时长和流量进行聚类,得出3种用户行为,并利用聚类结果为校园网用户个性化需求方面提供理论依据。文献[6]利用优化层次聚类算法对校园网主干数据流的IP地址进行聚类,得到网络用户的访问地址分布情况,从中了解用户行为特征。文献[7]提出结合网络用户数据特点的预处理方式,并引入基于图论的子空间聚类方法、粒子群聚类算法得到校园网用户网络行为模式。文献[8]利用K-means算法和统计技术对校园网用户日志数据进行分析,发现大部分学生每个月上网时间小于170小时、学生上网时间越长越容易挂科的规律。文献[9]对Concordia大学Wi-Fi日志数据利用PCA制导的聚类算法进行分析,得到7类行为模式,并给出多天同类型活动的搜索算法。
上述研究中,聚类中采用上网时间都是用户一天或者一个月为单位的上网时间,大多数研究没有去除脏数据。本文将学生上网认证数据转换为24小时时长向量,保留较多细节,更方便分析学生上网时刻及更能反映学生上网时间分布规律;采用改进Canopy算法,即K-canopy算法,去除离群点,提高聚类质量,进而提高分析结论的可靠性。本文首先选择校园网认证数据并对其进行清洗,去除与研究目标无关的数据;然后进行数据预处理,得到学生上网时长向量集;再对学生工作日和周末的上网时长向量分别进行聚类。最后依据聚类结果分析了各类学生上网时间和时长分布特征,结合年级专业上网规律进行总结,为学生管理、专业课程设置等工作提供参考。
1 数据预处理
本文选择校园网2016年11月本科生的认证数据进行实验分析。因为11月份是正常学期时间,不受开学、期末考试影响,且11月假期较少,更能全面反映学生上网行为分布规律。在数据预处理阶段,首先进行数据清洗,去掉与研究目标无关的数据,然后计算每个用户、每天24小时内每小时的上网时长,得到上网时长向量集合。
1.1 数据源说明
本文实验数据来源于SAM网络认证计费系统和Syslog网络设备日志收集系统。主要提供的信息有:用户帐号、IP地址信息、上线时间、下线时间和离线原因等。表1给出源数据表中关键字段说明。
1.2 数据预处理
(1) 数据选择:校园网认证记录数据量比较大,其中包括本科生、研究生、教职工和住宅区等多种类型账号的认证数据,也包括了线路故障反复登录、设备自动登录等其他与本研究无关的认证数据。针对本文研究目标,下面详细列出需要清洗的数据及其清洗原因和处理策略。
① 研究生、教职工、办公区、来访人员和住宅区等非本科生认证数据。此类数据与本研究无关,依据帐号特征去除该类数据。
② 大学一、五年级学生认证数据。学校规定仅有少量满足特殊条件的一年级学生可开设校园网帐号,五年级学生是特殊专业或者学籍异动的学生,此类学生不具有代表性,依据帐号特征去除。
③ 去除11日的数据。双11购物节,按学校规定10-11日夜间不断网,因此这一天学生的上网行为不是常规工作日行为或者周末行为,属于异常行为,直接删除该时间段全部认证记录。
④ 上下线时间间隔小于或等于60秒的数据。机器故障所产生的,这类数据对分析学生上网行为没有意义,依据上下线时间计算时长,然后去除该类数据。
⑤ 单次在线时长超过48个小时的数据。可能是设备挂机或者是个人极端行为,这类数据不反映学生上网行为或者不具有代表性。依据上下线时间计算时长,然后去除该类数据。
⑥ 从6点钟到23点钟时间段内上网时长都是3 600秒的数据。设备自动认证数据,不反映学生上网行为,依据帐号每小时上网时长去除该类数据。
综上所述,本文实验数据范围:全月原始数据有1 990 396条认证数据,其中工作日数据1 487 914条,周末502 482条。清洗后总数据量201 523条,其中工作日152 007条,周末49 516条。
(2) 实验数据预处理:本小节对学生每天产生的多条上网认证数据进行处理,得到每个学生每天的上网时长向量。计算每个学生每天24小时上网时长向量,从而将学生一天上网时长细化到每天每小时,更能反映学生上网时间分布。为保护学生隐私,本文对用户帐号进行了脱敏处理,利用无意义的数字替代敏感信息。
表2给出学号为2013000XXXX的学生在2016年11月2日的认证数据预处理结果,假设其上网时长向量m,那么m值如下:
m=[2013000XXXX,2016/11/2,0,0,0,0,0,0,0,0,876,2 278,0,0,0,2 626,3 600,3 600,3 018,0,2 400,3 600,3 600,3 530,3 600,1 799]
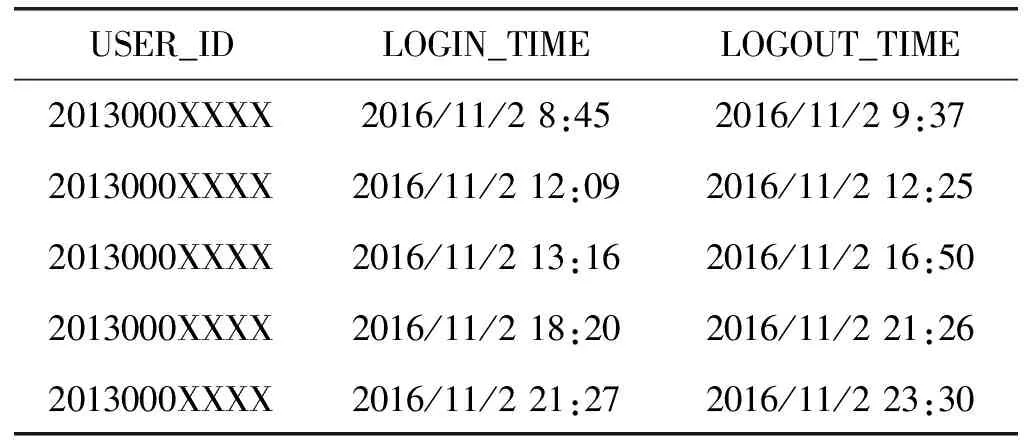
表2 认证数据表
2 粗聚类与聚类
2.1 粗聚类
本小节使用K-canopy算法对上网时长向量集进行粗聚类,去除离群点并估计聚类个数。
Canopy算法一般称为粗聚类算法,它不需要指定聚类个数,算法简单,运算速度快[10]。Canopy算法原理和实现方法见文献[11]。本文基于Canopy算法基本原理设计并实现K-canopy聚类算法,用于去除离群点。K-canopy聚类算法的基本思想是首先利用Canopy算法对数据进行一次粗聚类,取数据个数少且聚类中心与其他Canopy中心距离较远的Canopy作为离群点去掉。重复此操作直到去掉总数据量的2%~5%的离群数据为止。按常规,2%~5%的数据为离群点是合理的,具体数量可依据数据质量、学生实际上网特征异常的人数来设定,以下是K-canopy聚类算法步骤。
(1) 构造原始数据集合List,计算全部数据两两之间的欧式距离的均值T,令T1=0.65×T;
(2) 在List中随机选取一个样本数据作为基点P,将其从List删除,并计算List中其他样本点到基点P的距离d1;
(3) 把d1小于T1的样本划到一个Canopy中,同时把这些已划分好的数据从原始数据集合List中移除;
(4) 重复(2)、(3),直到List为空;
(5) 开始发现异常点,构造由各个Canopy的中心组成的数据集合Center,令T2=0.95×T1;
(6) 从Center中顺序选取一个数据C,计算C与Center中其他所有数据的距离d2,统计d2小于T2的次数n,直到遍历Center;
(7)n小于或者等于2,则将由样本C生成的Canopy定义为一个异常类,其他Canopy定义为正常类,该异常类中的样本全部定义为离群点。
该算法中变量T、T1、T2和n是较重要的参数。T是两两向量之间距离的平均值,用来划分Canopy的阈值。对每个向量,若其与选定向量的距离小于T1,则被划分到选定向量所在的Canopy中,此处取T1=0.65×T是针对本实验数据经过多次实验后能有效避免数据倾斜现象而选定的。参数T2和n是划分离群点所在类的阈值。若一个类与其他类的中心之间的距离小于T2的次数少于或等于2次,则说明此类的中心与其他类的中心距离较远。如果类包含向量个数少于200,则此类中所有向量为离群点。此处取T2=0.95×T1、n=2、类中向量个数小于200是针对本实验上网时长向量集多次实验选定的。对其他数据集,可选择不同参数。本文为达到更好的粗聚类结果,对向量集循环了20次K-canopy聚类算法。
由于学校工作日和周末的断网策略不同,本文将工作日和周末分别粗聚类。工作日粗聚类后得到148个Canopy,其中包含6个向量数量明显较大的Canopy,去除2 323个离群点,占比1.53%;周末粗聚类后得到106个Canopy,其中包含5个向量数量明显较大的Canopy,去除3 627个离群点,占比7.32%。通过分析发现,去除的向量确实与其他向量差异较大。
2.2 K-均值聚类算法描述
K值,即聚类个数,是K-均值聚类算法(K-means算法)中最重要的参数,会极大地影响聚类结果。确定K值的思路有很多种[12-14]。本文采用投票机制,即利用多种指标最终确定K值。在对数据样本分布缺乏先验的理解前提下,本文选择稳定性较好的三种指标,分别是轮廓系数[15]、戴维森堡丁指数(DBI)[16]与误差平方和系数(SSE)[17]。轮廓系数、戴维森堡丁指数侧重于类间间隔性与类内紧密性,轮廓系数越大、戴维森堡丁指数越小说明聚类效果好。误差平方和系数则是常规K-means算法的损失函数,可以直接表现出聚类效果[18]。
K-means算法是一种简单、收敛速度快、易实现的经典聚类算法,适用于数值型数据集聚类。该算法的核心思想是找出K个聚类中心,使得每一个样本点和与其最近的聚类中心的平方距离和被最小化[19]。本文K-means算法流程如下:
(1) 根据K-canopy聚类得到最优K值,并从数据集中随机选取K个样本点作为初始中心点;
(2) 计算各个样本点到各个中心点的距离,并将其归类到距离最小时对应的类;
(3) 根据聚类结果,重新计算每一个类的中心值;
(4) 重复(2)、(3),直到每一个类的中心值稳定或者迭代次数超过给定阈值。
本文首先依据K-canopy算法计算结果中向量个数明显较大的Canopy个数,粗略得出K值范围;然后对范围内每个K值的每一个指标都进行10次K-means聚类再求均值,以降低随机性影响;再利用投票原则来选取最优K值;最后通过K-means聚类算法对数据集进行聚类。
综上,本文最终得到的工作日学生的上网行为聚类个数即K值为6,周末聚类个数即K值为5。通过实验结果可发现本文对工作日和周末数据聚类所得到的K值可得到较好的聚类效果。
3 聚类结果与分析
本文实验使用Java编程语言实现,主机的CPU型号为CPUi7-8700K,内存为8 GB,操作系统为Microsoft Windows 10。
由于工作日和周末的断网策略不同,且学生课程安排也不一样,学生的行为也存在较大差异,因此本文将周末和工作日数据分开处理。以下是整体的实验流程:(1) 选择校园网2016年11月本科生的认证数据,并对其预处理得到上网时长向量集合;(2) 利用K-canopy算法对得到上网时长向量集进行粗聚类,去除离群点并估计聚类个数;(3) 利用K-means算法和估计聚类个数对去除离群点后的上网时长向量集合进行进一步聚类,并使用三种指标对聚类结果进行评价,选择出最优的聚类个数和聚类结果。
3.1 工作日聚类结果与分析
以下先对工作日12天数据进行聚类分析。图1给出工作日聚类结果,图的横坐标是时间,代表24个时段,纵坐标为平均上网时长。曲线反应各类各时段上网平均时长。表3给出工作日各类中学生人数分布,按学生学号统计每类中学生人数。
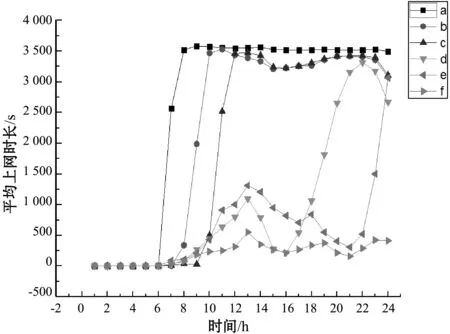
图1 工作日聚类结果
从图1和表3可总结工作日校园网用户的上网时间分布规律如下:
(1) a类学生和b类学生上网行为相似,都是白天长时间上网的学生。其中a类学生从早晨6点时段陆续开始上网,8点时段几乎全部上线,直到当天结束。b类学生在8点时段陆续开始上线,10点时段几乎全部上线,10点到16点时段有少量下线,16点时段到23点时段在线人数有细微波动,直到0点断网时全部下线。
a类学生人数少,占比为7.88%。其中,三个年级学生人数差距不大,分别占30.21%、35.84%和33.96%。本类学生工作日全天上网而且人数较少,说明上网应属个人行为,学生个人有网瘾的概率较高。b类学生人数中等,占比16.48%,明显大四、大二学生较多,分别占43.32%、35.66%。分析原因应该与学校各专业课程设计相关,是大二学生上午有课的较多,而大四学生上午没课的比例较大。
(2) c类学生在12点时段陆续开始上网,13时段上线在数达到最多,14点时段到22点时段有少量学生下线,22点到23点时段又有少量上线,直到24点断网。
此类学生人数占比16.54%,同样大三和大四学生较多,分别占36.70%和39.93%。分析原因同样应该是大三、大四学生下午没课的比例较大。
(3) d类学生白天上网较少,峰值出现在13点时段,但此时段时长均值仅1 100秒(约合18分钟)。13点时段后继续下线,至16点时段到达最低点,平均上网时间约180秒(约3分钟)。之后继续上线,至晚上22点时段时达到峰值,平均上网时长3 437秒(约57分钟)。之后继续下线,直到12点断网。
此类学生使用网络较少,工作时间基本不使用网络,上线时间集中在晚上7点-10点时段。此类学生总数点比较高,点18.30%,有10 398人。三四年级学生人数占比稍大,分别占35.85%和38.30%。
(4) e类学生与d类有些相似,白天上网较少,峰值出现在13点时段,该时段平均时长略高于d类学生,1 311秒(约22分钟)。其主要上网时间从21点时段开始陆续上网,至22点-23点时段达到峰值。其峰值比a-d类学生平均时长都少3 066秒,约51分钟。
此类学生工作日基本不使用网络,仅在晚上10点-11点时段上网。对大二、大三学生预计上课、自习时间较长,而对大四学生,可能因为参加实习等原因未在宿舍使用网络。
(5) f类学生全天在线时间最短,峰值出现在中午13点时段,此时段平均上网时长峰值也仅仅551秒,约9分钟。
此类学生上网行为与前面5类学生差异较大。此类学生总体占比23.95%,人数最多。在此类学生中同样大三、大四学生较多。
3.2 周末聚类结果与分析
与工作日分析相类似,本文对周末同样进行聚类分析。图2给出周末聚类结果,表4给出周末各类学生人数分布。
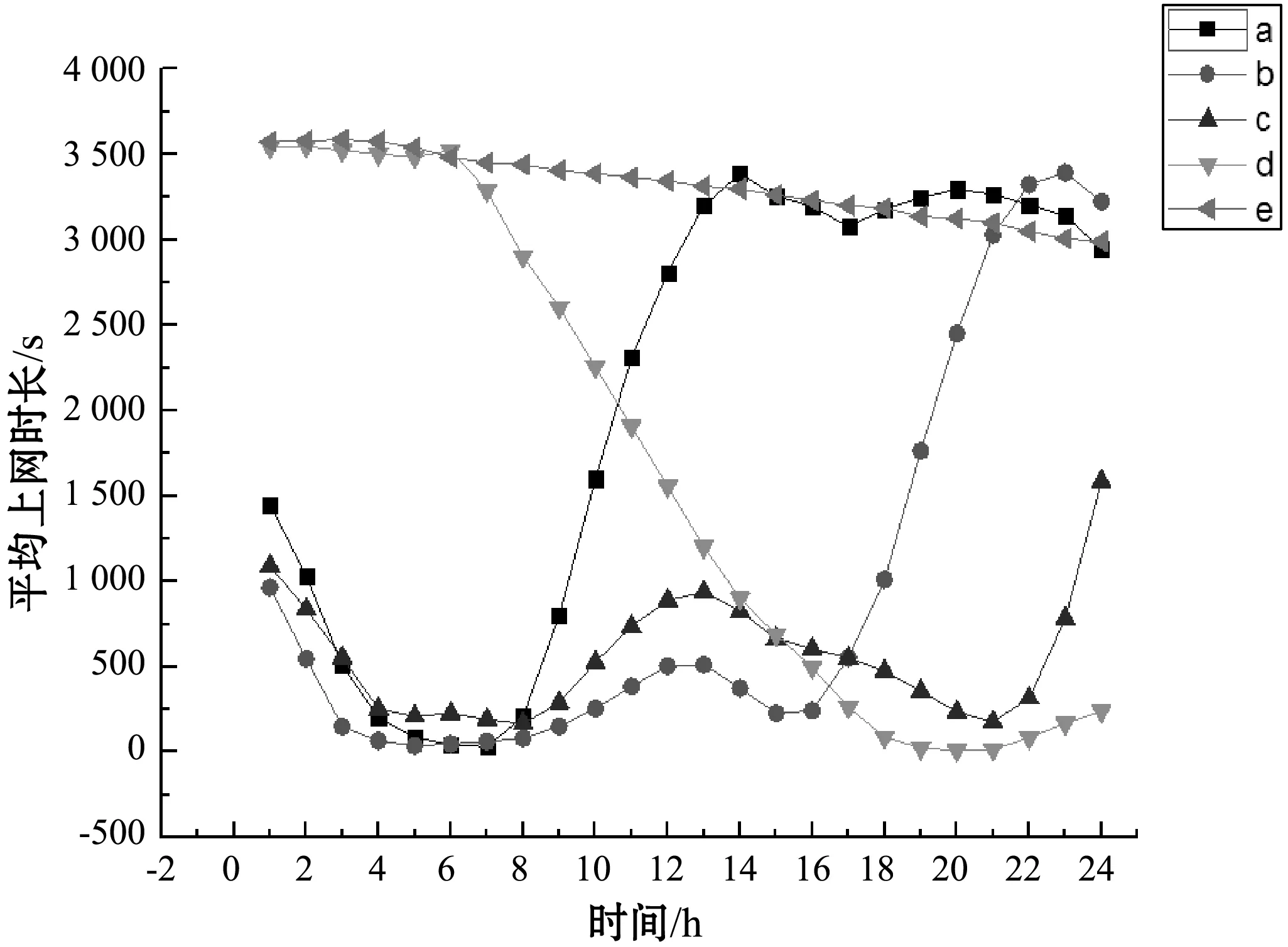
图2 周末聚类结果
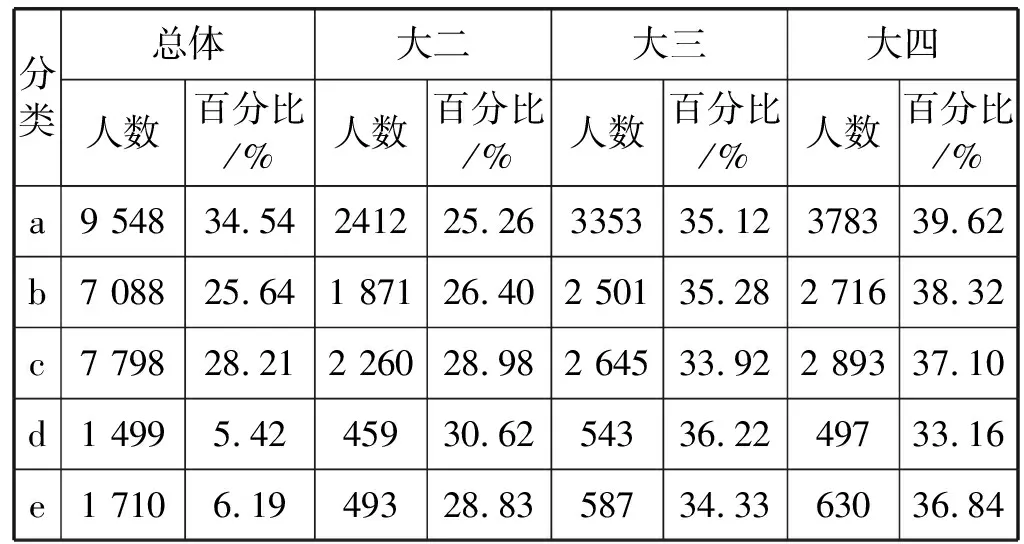
分类总体大二大三大四人数百分比/%人数百分比/%人数百分比/%人数百分比/%a9 54834.54241225.26335335.12378339.62b7 08825.641 87126.402 50135.282 71638.32c7 79828.212 26028.982 64533.922 89337.10d1 4995.4245930.6254336.2249733.16e1 7106.1949328.8358734.3363036.84
在周末,学校24小时不会断网,根据图2和表4总结出代表周末校园网用户的上网行为如下:
(1) a类学生周末会熬夜,在0点时段在线时长均值为1 449秒(约24分钟),说明约一半学生在线。从0点时段开始陆续下线,4点时段差才全部下线。之后上午8点时段开始陆续上线,至14点时段时多数学生上线,上网时长均值达到3 386秒(约56分钟)。从此时段直到晚23点时段此类学生大部分在线。
此类学生周末主要是白天长时间在线、会熬夜。总学生人数占比34.54%,是人数最多的一类。其中大二、大三、大四学生各占25.26%、35.12%、39.62%。
(2) b类学生周末熬夜,白天上网较少。在0点时段在线时长均值为963秒(约16分钟),说明有些学生熬夜,但人数比a类少。此类学生熬夜集中在0点-4点时段。白天上网时间不多,峰值出现在中午13点时段,均值512秒,约9分钟。下午在线人数少,晚上在线人数继续增加,23点时段达到峰值,平均时长为3 392秒(约57分钟)。
此类学生白天上网少,有少量学生会熬夜。占总人数的25.64%,其中大二、大三和大四年级学生各占26.40%、35.28%、38.32%。
(3) c类学生在线峰值出现在凌晨0点、中午13点和晚23点时段,但时长均值不大,最高1 587秒(约16分钟),说明最多约一半学生23点时在线。其他时间在线的学生不超过一半。
此类学生使用网络时长较短,少量熬夜,白天较少上网,人数占总人数的28.21%,比例较大。各级学生占比分别是28.98%、33.92%和37.10%。
(4) d类学生全部通宵,白天很少上网。这类学生从0点到6点多全部通宵,6点多后陆续下线,至19点时段的在线人数趋近0。22点时段开始又有少量学生开始上线,至23点时段在线时长均值为239秒(约4分钟)。
此类学生在总体中占比最少,为5.42%,人数1 499人。此类学生中三年级基本均衡,都占30%以上。
(5) e类0点到18点时段几乎在线上,在线时长均值达到59分钟。18点时段开始至24点有少量下线。此类学生在总体中占比6.19%,人数较少,约1 700人。且在此类三个年级人数相差不多,大四学生稍多,大二学生略少。
3.3 按个人及专业的上网时间特征
(1) 个人上网时间特征:针对每个学生,依据帐号可统计其上网时间分布所属的类,从而发现学生个人的上网时间分布。表5给出两个学生的上网时间分布。第一个学生工作日在线时间较少,有2天属b类、1天c类、2天d类、1天e类和5天f类。其工作日大约有2天工作时间在线、6天时间晚睡。周末白天上网较多,有2天可能晚睡,但未通宵熬夜。可知,此学生是正常上网的学生。第二个学生15天中有10个工作日上网行为属于a类,几乎工作时间都在线,周末又有4天属于a类,即白天几乎全在线,晚上有晚睡。此学生使用网络时间超长,有网瘾的可能性较大。此类学生需要统计后提请学生管理部门特别注意。通过聚类结果,可以很容易发现使用网络过多、过少或具有其他特征的学生,为学生管理部门提供建议。
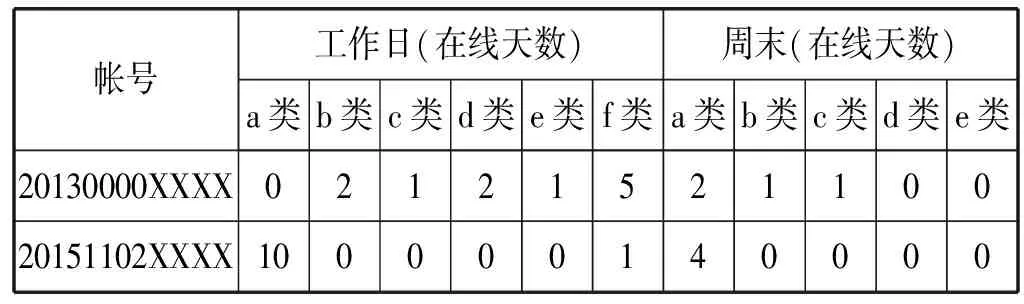
表5 某学生上网时间特征分布
(2) 各专业学生的上网时间特征:对各专业可统计每年级属于不同类的学生人数,再对比其他年级专业可发现各专业学生上网时间分布特征。作为示例,表6给出计算机科学技术专业学生总人数、上网人数、工作日和周末上网人数分布。
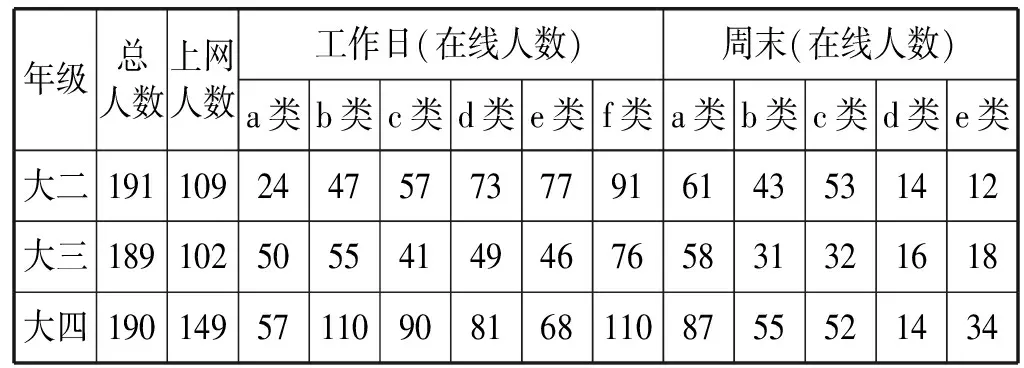
表6 此校计算机科学技术专业学生上网分布
从表6可知,三个年级总人数相似,大四学生上网人数较多(149人)。总体来看,工作日大二学生使用网络较少,晚睡、通宵的人数都比较少。大三使用网络人数有所增加,晚睡、通宵的人数也都有增加。大四学生上网人数增加,在各类中人数占比大,说明学生上网时间差异较大,可能因为课程设置较少,学生不受上课时间约束,自由度高。对于周末人数分布,大四学生使用网络最多,通宵、熬夜人最多。大二学生周末使用网络比大三学生多,熬夜通宵人数少于大三人数。
对其他专业可进行类似分析。当然也可通过数据对比获取各专业学生上网时间分布的差异。限于篇幅,本文未给出各专业对比情况。通过专业对比,可为专业设置、专业各年级课程设置提供参考。
4 结 语
本文选择2016年11月的校园网上网认证数据,清洗掉与研究目标无关的数据,然后计算得到学生的上网时长向量集合。对上网时长向量的聚类分三步进行,首先利用K-canopy算法选择并去除离群点数据,提高了数据质量和聚类效率,使聚类结果更具说服力。再用轮廓系数、戴维森堡丁指数与误差平方和系数三种参数投票确定最优聚类个数。最后利用K-means算法对工作日和周末上网时长向量集分别进行聚类,对聚类结果进行分析,得到工作日、周末不同类型学生上网时长特征。另外,统计单个学生、某专业各年级学生的聚类结果,分别得到对应的上网时长特征。本文分析结果可为专业课程安排、学生管理工作提供参考。
随着无线网络认证数据的暴增,学生上网行为信息更为丰富。因此下一步会利用Spark平台对有线、无线认证数据、网络流量数据及学生成绩等数据进行进一步分析,在校园人员流动规律、学生成绩与上网成绩关联性等方面获取更有价值的分析结果。

