Harris 算法和Susan 算法的实现及分析∗
崔 乐 李 春 李 英
(1.商洛学院电子信息与电气工程学院 商洛 726000)(2.陕西省尾矿资源综合利用重点实验室(商洛学院) 商洛 726000)
1 引言
特征提取是图像配准和图像分析的基础,是物体运动跟踪的关键步骤之一[1]。采用场景的几何和物理属性来产生图像中局部灰度级的显著变化,从而产生图像特征。图像特征的获取是成功进行相机立体视觉和校准研究的基础和前提[2]。图像的边缘点、纹理、角点、拐点等是图像特征的主要特点,标定精度和匹配精度受特征提取质量的直接影响。因此,提取角落信息在研究和处理图像中的重要信息中起着重要作用。
基于图像特征在图像处理中的重要性,国内外众多学者借助计算机视觉针对不同的实体物件开展了大量的研究工作。Ma Qin[3]等基于图像HSV颜色空间,获得了多玉米穗三维育种特征的快速测量方法,果穗的测量精度可达94%,从而大大提高了玉米品种的评价效率。梁文东[4]等利用Matlab,成功提取了指纹图像的特征点,并实现伪特征点的剔除,其算法简单、速度快且运算量小。王国林[5]等通过提取轮胎接地的投影面积、接触面积、印痕宽度和印痕长度等几何信息,实现了印痕几何参数的快速测量。然而,目前在计算机视觉和图像处理领域中没有适当的角点数学定义,但是有很多方法可以描述角点检测[6~10]。为了防止或减少错误特征的出现,许多方法都要求有大量的训练集和数据冗余来避免这种错误[11~12]。基于此,本文主要利用Matlab 提供的平台进行Harris 算法和Susan 算法的图像处理,并结合Matlab语言编写的程序实现两个算法的比较和分析。
2 Harris 角点检测和Susan 检测算法简介
2.1 Harris角点检测原理
对于一副照片,Harris 角点检测的原理是:通过局部图像的灰度变化程度反映给自相关函数,进而实现对角点的检测。Harris 算子是一个简单的点特征提取算子,它源于信号处理中的自相关函数,自相关函数的阶梯曲率是M矩阵的特征值[13]。
1988 年,C. Harris 和J. Stephens 提出一种基于信号的点特征提取算法,即Harris 算子,也称为Plessey 角点检测算法[14]。根据自相关函数的尖顶图像进行判断是该算法的核心,此尖顶处的点是角点。也就是说,通过建立对称矩阵M(与照片X 方向一阶导数和Y 方向一阶导数自相关函数相联系的矩阵),求得M的两个特征值,而自相关函数的一阶曲率是M 阵的特征值。若自相关函数图像在这一点呈尖顶形,则说明两个曲率值都很高。对于图像I(x,y),在点(x,y)处平移(Dx,Dy)之后的自相似性可以通过自相关函数给出:

其中,W(x,y)是以点(x,y)为中心的窗口,w(x,y)为加权函数,可以用常数或者高斯加权函数表示。
根据Taylor 展开,在平移(Dx,Dy) 后对图像I(x,y)执行一阶近似:

在式(2)中,Ix、Iy是图像I(x,y)的偏导数。这样,式(1)就能近似表示为

其中:
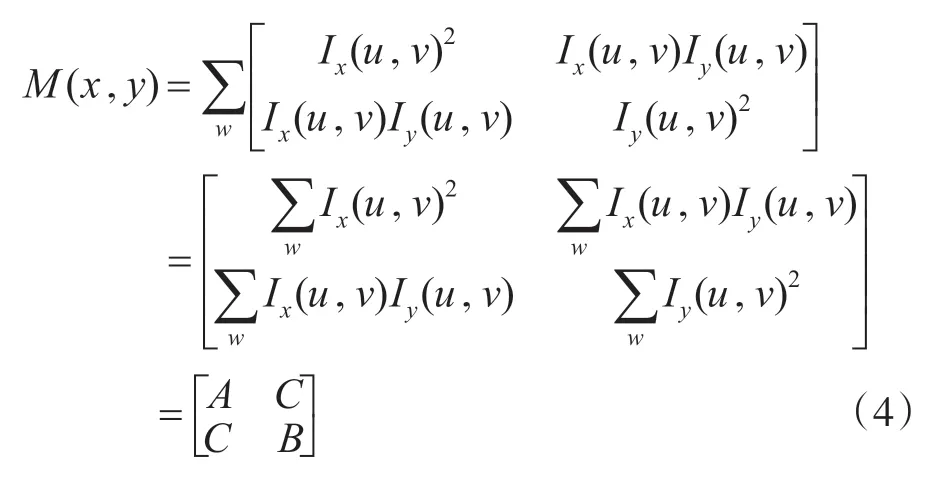
在图像I(x,y)在点(x,y)处平移(Dx,Dy)后,其自相关函数可近似为

根据二次函数的特征值计算方法,可以得到等式(4)的特征值。Harris 算法中给出的角点辨别方法不需要计算特定的特征值,而是计算角点响应值R以确定角点。R的计算公式为


Harris角点检测实现步骤如下:
1)求出I(x,y)在x、y方向上的的梯度Ix、Iy;
2)分别求出在x、y 方向上的梯度乘积,I2x=Ix⋅Ix,I2y=Iy⋅Iy,Ixy=Ix⋅Iy;
3)对I2x、I2y和Ixy执行高斯加权,从而产生三个元素A、B和C,如下所示:

4)获得每个像素的Harris 响应值R,使得小于阈值的响应值R为零;

5)进行3 3邻域非极大值抑制,并且图像中的角点由局部极大值点表示;
6)记录图像角点的位置。
2.2 Susan角点检测原理
由于Susan 算法无需计算梯度,因此非常适用于噪声图像或者低对比度的灰度图像的边缘检测。它具有噪声能力强、定位准确等特点,可直接与图像灰度的相似性进行比较。此算法不但运算量少,也能够达到细化边缘的目的[15]。
1)算法描述
对于图像中的所有像素,利用设置的圆形模板扫描整个图像,并将模板内的每个像素与中心像素的灰度值进行比较,通过与设定的阈值进行比较,判断像素是否在Susan 区域内,并且定义的区域由式(8)表示:
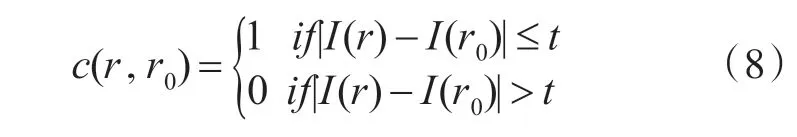
式中:c(r,r0)为模板中属于Susan 区域的像素判别函数,I(r0)为中心像素的灰度值,I(r)是模板内任何像素的灰度值,t为灰度差门限。那么,图像中某一点Susan区域的大小可以表示为

式中c(r0)是以r0为圆心的圆形模板部分。获得每一个像素的Susan 的n(r0)以后,将其与先前设置的阈值进行比较,当n(r0)<g 时,检测到的像素位置r0可以被区分为边缘点。
2)模板的选择
实际上,不能实现常规的循环模板。然而模板较小的时候,如果出现边缘点漏检的现象,则是由于门限值选取的不恰当。所以为了不增加运算量,模板也就不适合取的过大,通常可以取5*5 或象素为37 的模板[16]。本文图像处理时都是采用的5*5的模板。
3)门限t,g的确定
门限g 确定边缘点Susan 区域最大值,假设照片中像素的Susan 值小于g,那么该点被视为边缘点。当g 太小时,将丢失部分边缘点;当g 太大时,可以选择边缘点附近的像素作为边缘。选取出初始的边缘点要有一定的质量,进一步删除其中冗余象素,则就有可能实现单象素的精度。
可以检测的边缘点的最小对比度由阈值t 表示,阈值t也是可以忽略的最大噪声容限。要从对比度较低的照片中提取特征,需要使用较小的t值。因此,采用不同的t值,可以获得不同噪声条件和对比度的图像。
3 基于Harris角点算法的实现
图1 所示为cnt分别为534 和2000 时,Harris 算法近距离采集照片的图像。从图中分析可得:对近距离采集的图像进行Harris 算法处理可较精准地标定出目标图像的轮廓,且计算速度快。有助于进一步对目标图形做更精确的处理,可无需对剩余部分图像再做相同处理。

图1 Harris算法近距离采集照片的实现
图2 所示为Harris算法远距离采集照片时的图像。从图中可以看出:对较远距离采集的图像做相同的Harris 算法处理,效果远差于近距离图像的,目标图像太远,故而所得图像包含太多除目标图像以外的部分,虽然角点信息量大,但对目标图像干扰大,究其原因在于Harris 算法的抗干扰能力弱,从而造成误差很大,同时,所检测目标物体的运动状态以及光线的明暗程度对其也有较大的影响。

图2 Harris算法远距离采集照片的实现
为了进一步分析Harris 角点检测过程中影响因素,图3显示了Harris角点检测cnt与距离和光线之间的关系。由图3(a)可以看出:随着距离的增大,cnt值也逐渐增大,进而导致使得对目标图像的干扰愈来愈大,在检测过程中容易出现多连续的点,并存在严重的检漏现象。所以在实际应用中应注意,例如对行驶车辆摄像时应该调节摄像头的焦距,便于抓住关键图像的主要信息成分。图3(b)所示为cnt 值与光线的关系,随着光线增强,其cnt值增大,同时目标物体的运动状态对cnt 值有较大的影响,对于静止的车辆,其cnt值随光线增强的增大速率较大,而静止车辆较小。图像的灰度变化会明显改变cnt的值,结合图1 和图2 可知,cnt值的变化严重影响图像的轮廓标定,进而影响着所采集图像的清晰程度。
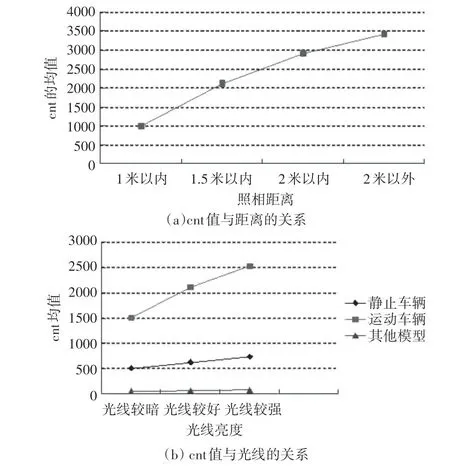
图3 Harris角点检测cnt与距离、光线的关系
综合以上分析检测结果,可以看出,Harris 算法的优点在于:可直接对原图像中的特征点进行检测,对兴趣点的检测不受图像的灰度变化、干扰噪声和旋转等因素的影响。然而其缺点也甚为明显,精确定位不够好,在有需要的情况下不能满足精确定位的要求。
4 基于Susan角点检测的实现
Susan算法用于检测道路区域中车辆的角点信息,然后获得原始图像中的特征点的二维坐标,最后确定相关信息。图4 所示为近距离光线良好情况下Susan 角点检测的实现。图4(a)显示出了车辆牌照号码的灰度处理之后的图片。车牌等物品自身污损较严重、拍摄的距离和角度、拍摄时光线的调节以及车辆的运动状态均会对图像的灰度处理造成一定的影响。目标物体清晰度越高,图像灰度处理后目标图像的轮廓越清楚,图4(a)是在较为理想的条件下得到的灰度处理图,故此,图像的灰度处理图较为清晰。图4(b)显示出了由Susan 算法处理的图4(a)的角点检测图,我们可以从处理后的图像清楚的看到轮廓,但所检测到的点有部分不连续,因此,可从更细微点对图像做进一步处理,得到更精准的图像。

图4 近距离光线良好情况下Susan角点检测的实现
为了进一步分析在远距离情况下,采用Susan算法能否实现图像的清晰检测,图5 给出了较远距离光线较暗情况下Susan 角点算法的实现。图5(a)显示了牌照状态和拍摄角度等的灰度处理图,类似于图4(a)。从图中可以看出,灰度处理后的图像清晰度类似于图4(a)的图像清晰度,这表明在灰度处理期间图像对其距离的影响很小。然而在采用Susan检测,在远距离检测过程中,有大量不连续的点出现,判断出图像的轮廓比较模糊,这样可能会漏掉图像中的重要信息,最终致使检测信息发生错误。

图5 较远距离光线较暗情况下Susan角点算法的实现图
图6 所示为Susan 角点检测图像清晰度与距离、光线强弱的关系,从图6 中可以看出:距离与光线可直接影响图像的清晰度,从而进一步影响Susan 算法处理的结果,也可以从图中判断出1m~1.5m 范围内采集的图像,经处理后,得到了更为清晰的图像轮廓,图像的形状更直观。

图6 清晰度与距离、光线强弱的关系图
综合以上分析检测结果可以看出,Susan 算法的优点在于:不需要去噪处理,不需要依赖于前期分割结果,而是直接利用图像灰度信息的检测算法。其缺点在于:自行设置的阈值会直接影响检测准确性,稳定性不够好。
5 结语
1)Harris 算法仅采用差分求导方式,易于计算,角点提取的可靠性比较高,稳定性和鲁班性较高,但抗噪能力较弱,很难实现准确的定位。
2)Susan 算法可以检测到任意类型的角,抗干扰能力也比较强,但其稳定性不好,图像检测的准确性取决于阈值的选取。
3)基于图像的灰度自相关函数的Harris 角点检测算法,能够直接从原始照片中检测到特征点,并且能够在照片自身发生灰度变化、旋转、和干扰噪声等情况下检测图像中的所有点。它达到了效率和精度两方面的要求,且抗噪能力有了很大提高,误检测率也降低。
4)直接利用图像灰度信息的Susan角点检测算法,要使检测过程不依赖前期分割结果,且不需要进行求导和梯度运算,那么它必须具有很强的抗干扰能力。与此同时,由于可以不用计算图像的灰度导数,因此不需要进行去噪处理,

