随机脉冲发展集值微分方程的可控性∗
李文胜 周 千
(西安航空学院理学院 西安 710077)
1 引言
近些年来,发展微分方程解的存在性问题得到了广泛关注[1~5],有关集值微分方程的内容可参见文献[6~11]。
本文在上述文献基础上,研究一类双参数发展系统下的随机脉冲发展集值微分方程:

2 预备知识
可测泛函x:Rτ→X 是Bochner 可积当且仅当‖ x ‖为Lebesgue 可积,有关Bochner 积分及其性质参见Yosida[12]。 L1( Rτ,X )是由Bochner 可积的连续泛函x:Rτ→X 组成的Banach 空间,赋予范数
引理1[13]设多值映射F 有非空紧值并且全连续,则F 是上半连续的当且仅当F 有闭图像(即当xn→x*,yn→y*,yn∈F( xn)时,有y*∈F( x*)。
引理2[13]如果F为Caratheodory 多值映射,且对给 定 的 ψ ∈B ,集 合 SF,ψ={f ∈L1( Rτ,X ):f( t )∈F( t,ψ ),t ∈Rτ} 是 非 空 的,Γ:L1( Rτ,X )→C( Rτ,X)为 线 性 连 续 映 射,则 Γ ◦SF:C( Rτ,X )→Pcp,cv(C ( Rτ,X )),y →( Γ ◦SF)( y )=Γ( SF,y)是C( Rτ,X )×C( Rτ,X )上的闭图算子。
有关多值映射和双参数发展系统可参见文献[13~16]。在证明过程中,本文将采用一个文献[17]提到过的公理化定义,
定义1泛函{ x ( t ):t0-r ≤t ≤T }称为(1)~(3)的温和解,当且仅当

其中

引理3[18]设B 为Banach空间X 中的有界的凸子集,Γ:B →P( B )是上半连续的凝聚集值映射,假如对任意的x ∈B,Γ( x )是B 中的闭凸子集,则Γ在B 中存在一个不动点。
3 主要结果
为了证明(1)~(3)是可控的,假定下面条件成立:
H2.当t >s 时,U( t,s )是紧算子,且存在一个常数M >0 ,使得当0 ≤s ≤t ≤T 时,有‖ U ( t,s )‖≤M 。
H3. 当t ∈J 时,存在一个常数M1>0 ,使得
H4.函数Q:Rτ×Cˉ→X 是连续的,且存在常数L,Lg>0,使得对任意的ψ,ψ1,ψ2∈B,有

H5(i)F:Rτ×→Pbd,cp,cv( X ),对每个ψ ∈,t →F( t,ψ )是可测的;对任意的t ∈Rτ,ψ →F( t,ψ)是 上 半 连 续 的;对 固 定 的ψ ∈B ,集 合SF,ψ={f ∈L1( Rτ,X ):f( t )∈F( t,ψ )a.e.t ∈Rτ} 是非空的。
H5(ii)存在一个可积函数m:Rτ→[0 ,+∞ )和一 个 连 续 非 减 函 数W:[ 0 ,∞ )→( 0 ,∞ ),使 得‖ F( t,ψ )‖=sup{‖ f ‖:f( t )∈F( t,ψ )}≤m( t )W(‖ ψ‖B),( t,ψ )∈Rτ×。
定理1假设条件H1~H5成立。如果
则系统(1)~(3)的是可控的。
证明:定义如下控制:
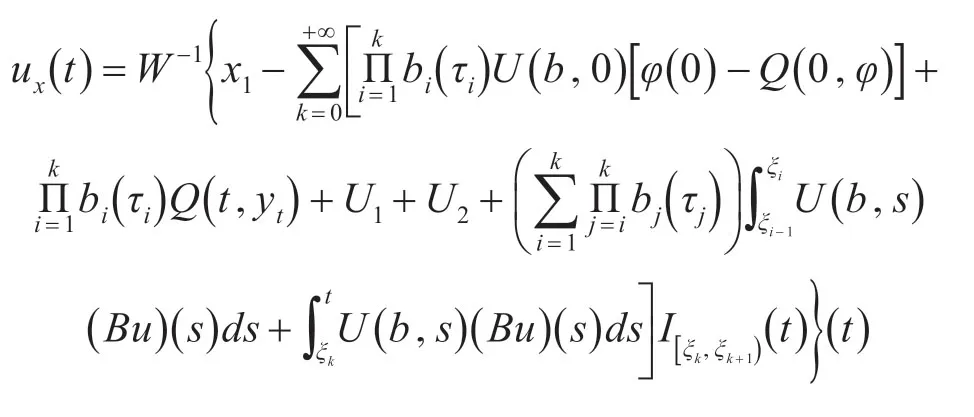
在赋予一致收敛范数的空间Y={u∈C(J,X ):u(0)=φ( 0)}上定义算子Γ:Y →P(Y),定义如下:
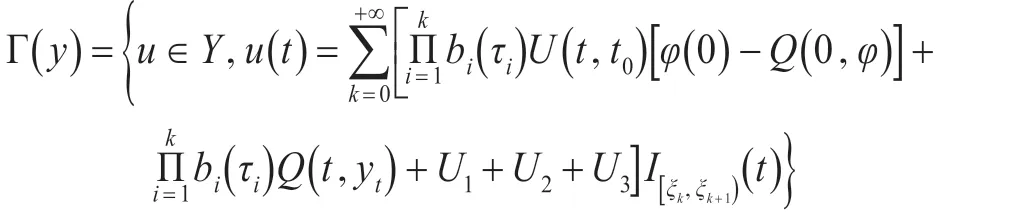
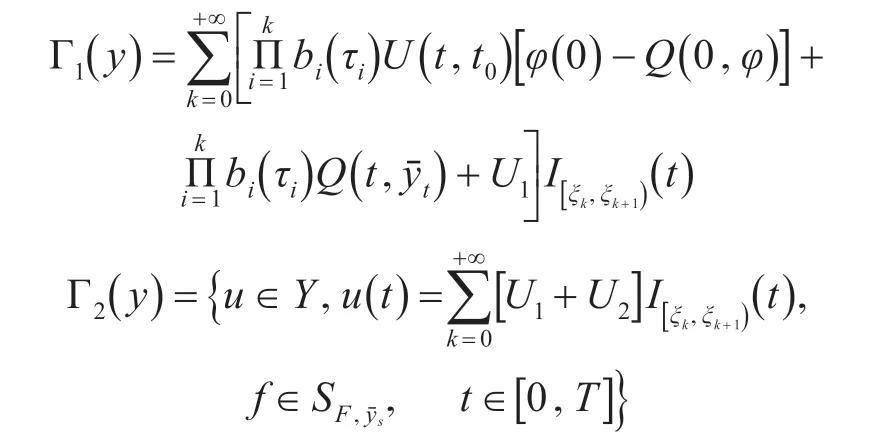
分以下几步来证明温和解的存在性:
第一步,Γ1是压缩的。
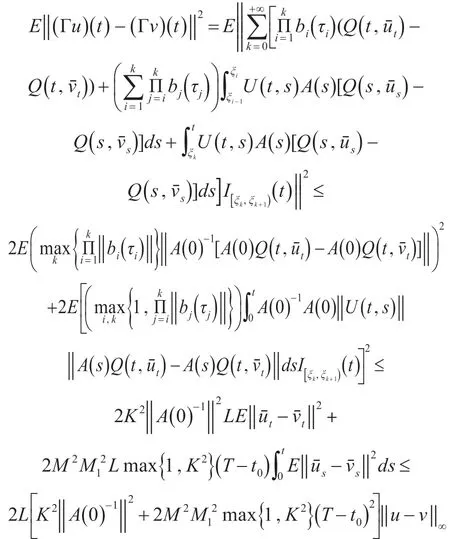
由(4)可知,Γ1是一个压缩算子。
第二步,Γ2有闭图。
令yn→y*,yn∈Br,un∈Γ2( yn)及un→u*,需要证明u*∈Γ2( y*)。
若un∈Γ2( yn),则存在fn∈SF,yn,使得对任意的t ∈[t0,T ],有
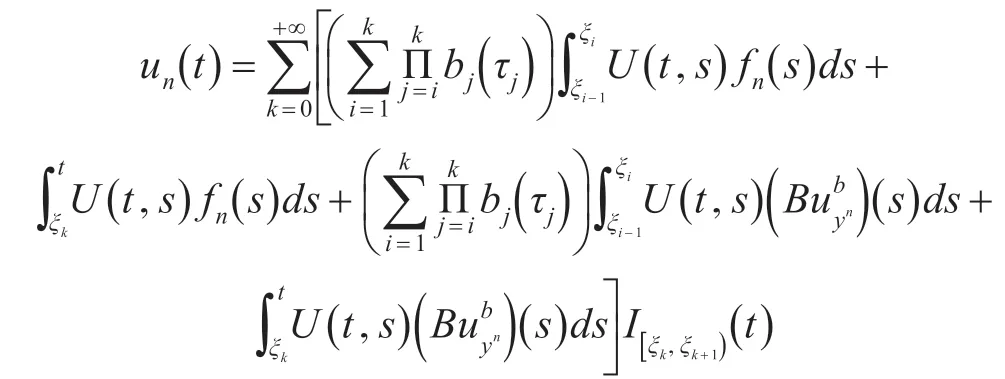
集合
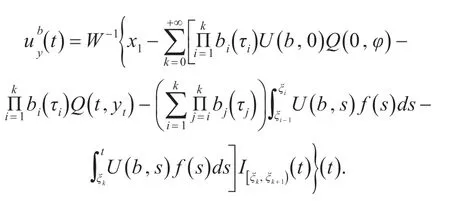
接下来证明存在f*∈SF,y*,使得
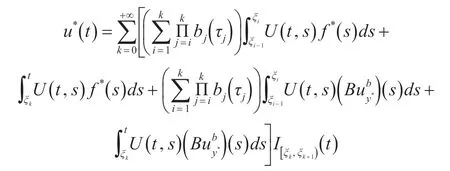
因此,Γ2是上半连续算子。Γ=Γ1+Γ2是上半连续且凝聚的。由引理3 可知,集值微分方程(1)~(3)是可控的。
4 结语
利用集值映射不动点定理结合发展系统理论,在随机脉冲有关理论以及抽象的相空间里所给定的充分条件的基础上,先将集值系统转化成积分方程,然后按照给定的集值映射不动点定理逐步证明了一类随机脉冲发展集值微分方程的可控性,此分析方法对同类集值微分系统可控性的研究具有一定的促进意义。

