依托数学活动经验发展合情推理能力
摘 要:对于合情推理能力的培养,是小学阶段学生数学学习和数学教学过程中的核心内容之一,本文着眼于依托以往的数学活动经验来发展学生的合情推理能力话题展开探讨,作者结合个人在这方面的一些实践工作经验提出几点思考,希望参阅者提出宝贵意见。
关键词:合情推理;推理能力;推理素材;教学经验;教学活动
合情推理能力属于学生在小学阶段基本的数学学习核心问题之一。新课程标准中对此也是做了明确要求:推理作为基本的数学学习的思维方式,它又是人们在学习和生活当中常常使用到的思维形式。所以,作为一名数学教师,就要在日常的教学活动当中给学生渗透合情推理,它要求在教学的内容以及材料方面都必须要合理,并且提出要分层次,分阶段性使得推理思想完全的贯穿于数学课堂教学的过程当中,基于此,我们也提出了关于“数与代数”“几何与图形”“统计与概率“综合与实践”四个领域的教学策略。
一、 深入挖掘合情推理素材,让学生经历推理活动
在小学数学中包括数学公式、数学法则、数学性质都是很久以前数学家们通过合情推理的方法得到的,与此同时,其也是数学推理过程中的最佳素材。如此对于教师而言,就必须要多研究数学教材,寻找到能够挖掘学生合情推理能力培养的内容来帮助学生学习数学及掌握推理方法。举个简单的例子,苏教版教材五年级下册第五单元部分有出现“分数的加法与减法”一节内容,首先教材给了几道列式,并且这些列式都是根据生活实际问题列出来的,紧接着题目又结合描一描,画一画的形式来充分说明分数加法的具体运算过程,最后也对其进行总结,得出了一些计算法则。
师:现在老师要求大家首先阅读一下题目——A小学有长方形的试验田一块,这块地里种着黄瓜和番茄。现在要求大家解答在这块地中,种黄瓜和种番茄的占比各是多少?列式计算。
生A:分子部分1+1=2,分母部分2+4=6因此,得到的答案也就是2/6,化简得到1/3。
生B:我不同意他的说法,我用画图的方法得到的答案是1/4。
生C:他们两人的答案我都不同意,分母是不相同的,即就是分数单位不相同,因此,它是不能够直接加起来的,我先把它通分化成同分母分数,然后再计算得到结果是1/5。
师:通过大家的努力,最终我们解决了分数加法题目,紧接着再回想一下我们使用的是什么方法?
生:如果遇到的分数分母不同,那么在做加法的时候要先对其通分将其转化成为同分母分数,之后再进行计算,能约分的一定要约分。
此教学片段实际上我们采用的是开放式教学方法,也就是让学生在自己思考的基础上总结出分数加法的计算法则,并且采用不同的方法来锻炼学生的思维,这就使得学生完全经历了由数字到推理的一个具体的过程,并且从中归纳总结得到了最终我们想要得到的答案。
二、 构建合情推理桥梁,让学生推理有理有据
学生能够展开合情推理的具体条件是基于在学生头脑中已经形成了同化新知的相关学习经验,此经验既能够是生活经验,同时也可以是知识经验。小学生的思维具有具体直观的特点,也正是因为如此,学生在做推理计算的时候,往往会用到他们已经学过的图形来实施计算或者类比推理。举个简单的例子,苏教版教材小学五年级上册数学教材有一节内容是“多边形的面积”,要求学生要在熟悉三角形和平行四边形以及梯形等一些规则图形面积计算的基础上,采用图形分割法或者填补法解决给出的问题。
师:某小学在校园里有块儿草坪,问题给大家,你们能否计算出它的面积大小是多少呢?(图略)
生A:计算的时候我将该图形分割成了长方形和梯形,而长方形的面积为12×4=48平方米,而梯形的面积为(12+15)×(10-4)/2=81平方米,如此就得到该不规则图形的面积就为81+48=129平方米。
生B:我将这个不规则图形分割成三角形和长方形,三角形的面积为3×6/2=9平方米,长方形的面积为12×10=120平方米,这样这个不规则的图形面积应该就是120+9=129。
生C:首先我将这个不规则的图形补成长方形,然后再用长方形的面积将梯形的面积减掉,就得到了我们想要得到的结果,长方形面积为15×10=150,而梯形的面积则为(4+10)×3/2=21,接下来用150-21=129,那么这块草坪的面積也应该就是129平方米。
师:大家都很棒,能用自己的方法解决这些问题,现在来想一想大家在割补的时候需要注意什么或者考虑什么问题?
生:对此我们需要结合原来图形的特点来做进一步的思考,然后再利用已知条件来计算见到的图形面积,当然可以采用不同的方法进行割补。
在这个教学片段中,学生遇到新问题时,通过合情推理构建起“已知知识”和“未知知识”之间的桥梁,使得学生能顺利地找到问题的突破口。这样的教学安排不仅降低了学生的思维难度,还有助于教师在教学中渗透类比推理思想,帮助学生解决不规则图形面积的计算问题。
在此教学片段当中,学生往往在遇到新问题的时候都要运用合情推理的方法来构建已知知识与未知知识之间具备的桥梁,促使学生可以在做题的时候顺利的找到题目的突破口。如此学生在学习的过程中难度不仅降低了,这对于教师帮助学生理解和运用类比推理的方法也很有帮助,借这个方法来解决学生日常生活中不规则图形的面积计算问题。
三、 借助线段图,让推理直观可操作
在小学阶段的数学教学中,可以适当地借助线段图来实施教学,这样就能化难为易,将抽象的问题变得具体化,同时也可以有效的帮助学生展开合情推理。
举个例子,学生问老师:“你今年多大了?”老师回答说:“我像你这么大的时候,你才3岁,而你像我这么大的时候,老师已经39岁了,现在你告诉我,老师今年多少岁了呢?”
如果该问题不借助线段图进行直接观察,那么绝大多数都比较难于理解题目当中具体隐藏的条件,那么推理也就很难展开。但是假如用线段图来表示,这对学生在头脑中形成正确的表象会很有帮助。
首先从0岁起画,学生3岁,而老师应该是学生现在的年龄,这当中两个人有一个时间差,与此同时,老师和学生之间现在的年龄同样存在一样的年龄差,如果学生长到了老师这个年龄的时候,这个时候老师已经39岁了,又隔了一段年龄差,换言之,39-3=36,36/3=12,它们之间相差了12岁,那么老师的年龄就是39-12=27岁。
再举个例子,A、B、C、D、E五位学生参加羽毛球比赛,比赛规则是每两个人进行一场比赛,裁判在中途做了统计,其中A同学共比了4场,B同学比了3场,C同学比了2场,D同学比了1场,问题是E同学比了几场呢?如果这道题目我们不用线段图来分析,学生一定手足无措,不知该从何下手。我们画图来进行解析:
A同学比了4场,也就是他和其他每个人都比了1场,D同学比了1场,那么他肯定是和A同学比了,其他同学他没有比,然后再有B同学比了3场,那么他肯定是除D同学之外与其他3个人都比了,C同学比了2场,这个时候就有他和A、B两个同学各比了一场,所以我们推断出,E同学仅与A、B两名同学分别比了1场,也就是2场。
四、 通过枚举,合情推理
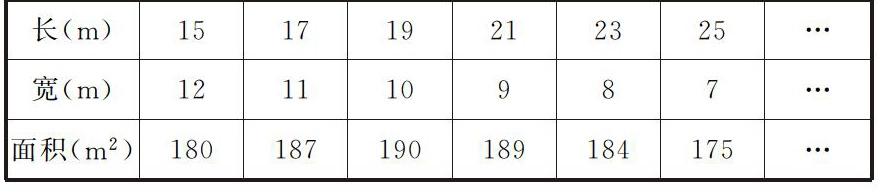
在小学数学中,采用一一枚举的方法,能很清楚地看到一些规律前后的变化,这对问题的解决很有帮助,举个例子,王阿姨用长39米的草绳围成了一个长方形的篱笆,并且长和宽都取整数,问题是,当长和宽分别是多少的时候,所围成的长方形的篱笆面积最大?
在分析过程中,教师方面可以引导学生展开自主探究。
由列表得到,长为15m,宽为12m,此时长方形的面积为180平方米;长为19m,宽为10m的时候,此时长方形的面积190平方米,然后当长分別为21/23/25m的时候,长方形的面积开始逐渐呈现递减的趋势,由189平方米逐渐减少到了175平方米。
有一些题目在进行枚举的时候往往需要适时地调控和矫正,同时推理的过程也要合乎情理。
例如,现要求将1~9个数字填入九宫格中,并且要求其横排、竖排、斜排的和都相等。
如果想要将1~9九个数字填入九宫格,并使得横排、竖排以及斜排的数字相加之和都相等,那么首先就可以求出来1+2+3+4+5+6+7+8+9……的和为45,每一排之和为45/3=15,如此我们可以来一一枚举一下,究竟哪些数字组合相加之和为15呢?
(1)1+9+5=15;2+8+5=15;3+7+5=15;4+6+5=15,能和5相加的另外两个数字只有这四组,所以介此推出来,九宫格中间的数字为5。那么也只有当数字5在中间的时候才能够保证横排、竖排和斜排的三个数字相加起来和等于15。
(2)9+2+4=15;8+1+6=15;8+3+4=15;7+6+2=15,在一番观察和思考之后,我们得到,在上面的8组数字中,和5相加的数字有4组,和8相加的数字有3组,和6相加的数字也有3组,他们分别是A组2+8+5=15,8+1+6=15,8+3+4=15,B组4+6+5=15,7+6+2=15,8+1+6=15,如此一来,我们就能合理的推断出8和6应该在九宫格的四角位置,但是他们又不可以在同一斜角上,原因是8+5+6=19,这样不符合要求,所以8和6应该在同一排的两个角上,中间只能是1。如此推理,很快就得出了8-5-2三个数字为一组,6-5-4三个数字为一组,1-5-9三个数字为一组,这样填起来也会容易许多,当然,在列举过程中我们同样要求数字不可重复出现,并且要求学生要养成良好的习惯。
五、 结语
推理能力应该当之无愧地属于是数学学习过程中的重要探索能力之一,除了逻辑推理,当然也有合情推理,即就是在进行数学推理的时候必须要保证其符合日常情理,不能原本是列举数字,学生给出来一连串汉字,这就不符合基本的推理原则,再者,本来1+1=2,再怎么推理也不能将其结果推出3来,这在数学领域的推理中是不成立的,并且它也是不科学的,不被允许的。合情推理教学生在推理的过程中必须要符合日常生活的实际实况,并且要符合自然万物的发展规律,如果超出了这些范围那么其就是不合理的推理,即不成立,所以,在实际推理中一定要注意到这一点。
参考文献:
[1]万福,于建福.教育观念的转变与更新[M].北京:中国和平出版社,2000.
[2]刘兼,孙晓天.数学课程标准解读[M].北京:北京师范大学出版社,2002.
[3]浙江省特级教师协会.特级教师论课堂教学改革[M].杭州:浙江教育出版社,2002.
[4]《人民教育》编辑部.新课程优秀教学设计与案例[M].海口:海南出版社,2003.
作者简介:
陈秀雄,福建省宁德市,霞浦县第四小学。

