基于多链接特征子集的聚类集成算法

陈彦萍，高宇坤，张恒山，夏 虹

1(西安邮电大学 计算机学院，西安 710121) 2(陕西省网络数据分析与智能处理重点实验室(西安邮电大学)，西安 710121)E-mail：821566504@qq.com

1 引 言

聚类作为重要的机器学习方法，对于复杂度高的数据集，单一的聚类算法很难正确地辨别出它的类簇结构，为了获得稳定且准确的聚类结果，人们提出了聚类集成算法.在很多方面聚类集成的性能都能够超越单个聚类算法的性能，如鲁棒性、稳定性和一致性估计.近年来，聚类集成已经成为机器学习领域中的热点研究问题之一，最初它是由Strehl和Ghosh[1]正式提出.Topchy等人[2]指出通过聚类集成算法得到的聚类结果要比单一聚类算法得到的结果好；而且聚类集成的结果受噪声和孤立点的影响，它们越少，结果的鲁棒性和稳定性越好.Fred和Jain[3]提出了一种证据累积的聚类集成算法(简称EAC)，首先计算所有基聚类结果的共联矩阵，然后使用最小生成树的分级聚类算法求得最终结果.周志华等人[4]将聚类集成与投票问题放在一起考虑，设计了一种投票机制，通过投票结果计算出聚类集成的结果.Naldi 和Carvalho等人[5]提出了一种基于相对有效指标的聚类集成选择算法，通过利用不同的有效指标进行聚类集成.Rafiee和Dlay等人[6]提出一种基于聚类集成的两阶段无监督分割算法，该算法能够从图像中提取自己指定的区域.杨林云等人[7]提出了一种基于模糊相似度量的软聚类集成算法，在软聚类集成算法中添加了三种模糊度量标准，提高了聚类集成结果的性能.王海深等人[8]提出了一种软投票聚类集成算法，首先将聚类结果进行重标签处理，使其标签对齐，接下来一对一相乘，最后设计一致性函数，做归一化处理.Lam-on和Boongoen等人[9]提出了一种基于链接的聚类集成算法，该算法解决了共联矩阵中信息使用不充分的问题，在生成共联矩阵时不仅考虑点与点之间的关系，还考虑了簇与簇之间的关系.Yousefnezhad等人[10]提出了一种利用群体智慧理论进行聚类集成的算法，该算法将群体智慧框架应用到聚类集成的问题中，获得了较好的聚类结果.江志良等人在文献[11]中提出了一种基于特征关系的加权投票聚类集成算法，该算法使用子数据集作为聚类成员的输入并使用加权投票的聚类集成算法，提高聚类的准确性和稳定性.在之前的聚类集成算法中，原始数据集中会存在冗余特征属性，而且相似度矩阵只能得到部分数据点之间的关系，对于具有弱相似度的数据点只能显示为0.为解决这些问题，本文提出了一种基于多链接特征子集的聚类集成算法(Clustering ensemble algorithm based on multi-link feature subset，CEBMLF)，该算法在基聚类结果的生成阶段使用独立特征选择法，消除了冗余特征，降低了原始数据集的维数，提高聚类集成结果的准确率；然后通过将数据点与簇的相关性集成信息矩阵转化为反映数据点之间的相关性关系矩阵，解决了相似度矩阵只能得到数据点之间的部分关系，对于具有弱相似度的数据点只能显示为0的缺点；融合基聚类结果的关系矩阵，使用Average-Linkage算法进行聚类，得到最终结果.该算法能使最终聚类的准确率得到提升.

2 相关概念

2.1 特征选取

特征选择是为了减少数据集的维数，消除重复无用的特征属性，所以本质上也可以称之为特征子集选择或属性选择.它是指从所有的特征中选择部分特征来优化系统的具体指标.从原始数据集的所有特征中选择出最有效的特征来代表原始数据集，以此达到减小数据集维数和消除重复无用的特征属性的目的，是提高学习算法性能的重要手段，同时它也是模式识别中数据预处理的关键步骤.

2.2 聚类集成

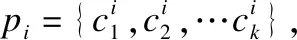
3 一种基于多链接特征子集的聚类集成算法

3.1 特征子集的选取算法

假设数据集X有M条数据{x1,x2,…,xM}和N个特征{d1,d2，…，dN}.将X表示为{D1，D2，…，DN}，其中Di为列向量(M维)，表示M条数据在第i个特征上的值.

在对数据集X进行聚类时，如果其中特征间的相关性很大，那么这次聚类使用的信息就会包含很多的重复信息，真实有用的信息就会很少.特征间的相关性指的是特征之间的独立程度或依赖程度.本文使用相关系数来计算特征之间的相关性.数据子集的选取要使得特征之间相互独立，所以要避免选取相关的特征，最好选取相互独立的特征.本文提出一种独立特征子集选取的算法，它以数据集的特征为基础，选出与其相关性最小的个特征，构成相对独立的数据特征子集.

算法1.独立特征子集选取算法

输入：数据集X={D1,D2，…，DN}.

输出：数据子集X*={D1,D2，…，Dk}.

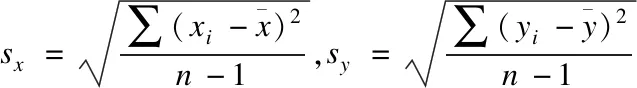
5.计算矩阵Xr中列向量的平均值Xc_mean；

6.选取Xc_mean中k个最接近0的值；

该算法考虑了所有特征的相关性，比随机抽取获得的结果要好，对于选择的特征个数k，本文在实验中通过聚类集成结果的RI值确定了的k的取值范围.

3.2 基聚类的生成策略

基聚类的生成有很多方法，如：用不同的聚类算法(k-means、层次聚集算法、谱聚类算法等)来生成基聚类结果；通过改变聚类算法的初始值、参数等设置，生成基聚类结果；通过不同的抽样方式得到数据子集，对数据子集进行聚类，生成基聚类结果；用不同的选择方法选取数据集的特征，生成特征子集，然后对特征子集进行聚类，得到基聚类结果.

本文首先从原始数据集中选取特征子集，然后使用多种不同的聚类算法得到基聚类结果.这样做能提高基聚类结果的独立性和多样性.

3.3 基于多链接的聚类集成算法

聚类的核心问题之一是如何构造数据点之间的相似度矩阵.本文借鉴连接三元组算法[9]的思想来构造数据点之间的相似度矩阵.

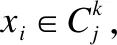
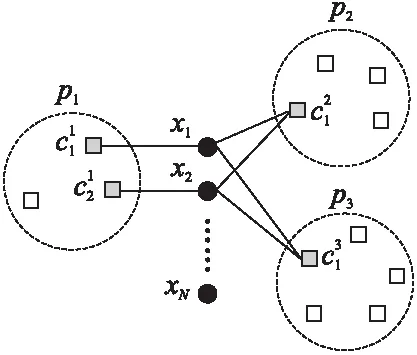
图1 多链接聚类示意图Fig.1 Multi-link clustering diagram

连接簇Ci和簇Cj的边的权重Wij由这两个簇共同包含的数据点个数得到，如下式：

(1)

其中，xi和xj分别为属于簇Ci和簇Cj的数据点的集合.邻接点为簇Ck的两个簇Ci，Cj之间连接三元组的值为：

(2)

簇Ci，Cj之间所有的三元组(1，…，q)可以计算为：

(3)

然后，Ci簇，Cj之间的相似度可以计算为：

(4)

其中WCTmax是任何两个簇WCT中最大的值，而DC是一个衰减因子.此时数据点xi，xj之间的相似度为：

(5)

其中C(xi)=C(xj)代表xi和xj在同一个簇中，C(xi)≠C(xj)表示xi和xj不在同一个簇中，此时的值为xi和xj分别所在簇的相似度.

融合基聚类后数据点xi，xj之的相似度矩阵为：

(6)

其中M为基聚类结果的个数，Nij表示样本i和样本j在M种划分中属于同一个簇时值为1，C(xi)=C(xj)代表xi和xj在同一个簇中，C(xi)≠C(xj)表示xi和xj不在同一个簇中.

算法2.基于多链接特征子集的聚类集成算法

输入：数据集X={x1，x2，…，xn}.

输出：最终结果T.

1.先使用算法1，得到独立的子集X*；

2.对X*使用不同的聚类算法得到不同的基聚类结果；

3.对每个基聚类结果使用公式(1)-公式(5)得到各自的相似度矩阵；

4.使用公式(6)融合所有基聚类结果的相似度矩阵；

5.对融合后的相似度矩阵使用Average-Linkage算法进行最终聚类，得到结果T.

4 实 验

在文中，我们利用标准数据集和它们的真实类比较了该算法与其他聚类集成算法的性能.所有的算法将在MATLAB R2016a中实现.表1是实验中用来产生基聚类结果的基聚类算法.

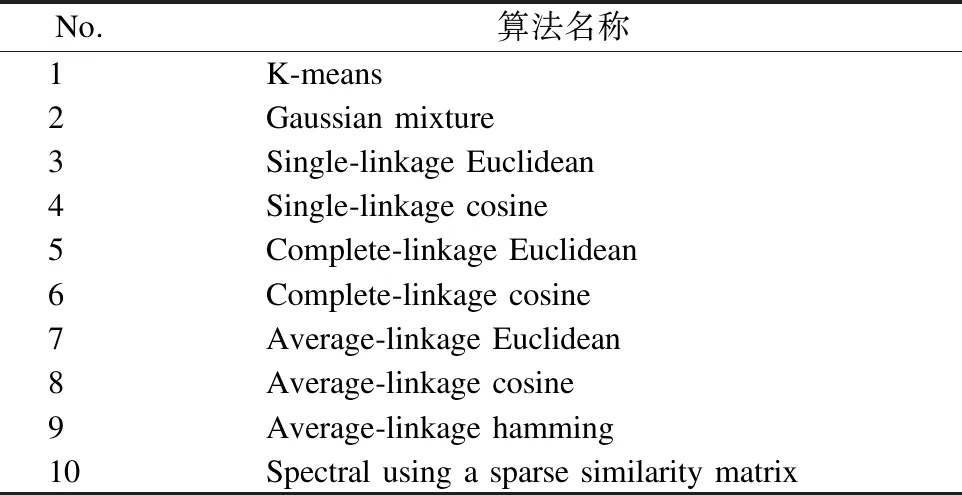
表1 实验所用的个体聚类算法Table 1 Individual clustering algorithm used in the experiment

4.1 实验数据及评价标准

本文从UCI[14]数据库中选取了9个数据集进行实验，见表2.

表2 实验所用UCI数据集Table 2 UCI data set used in the experiment

实验采用外部评价标准RI(rand index)[15]对聚类结果进行评价.RI有如下定义：

(7)

其中Y表示真实标签；T表示结果集；n11表示数据在T中和在Y中都在同一个簇中的数目；n00表示数据在中和在T中不在Y同一个簇中的数目；n10表示数据在T中在同一个簇中在Y中不在同一个簇中的数目；n01表示数据在T中不在同一个簇中在Y中在同一个簇中的数目.文献[15]中提出聚类的RI值越高，聚类的准确率越高.

4.2 实验设计及结果分析

设置基聚类成员个数，分别运行表1中的10种基聚类算法.为了降低结果的偶然性，最终的取值为集成算法运行10次的平均值.

为了证明独立特征选择法的优越性，本文引入随机抽样法与其进行对比，在表2的数据集中分别进行实验，使用本文提出的CEBMLF聚类集成算法，评价标准使用RI标准.得到的实验结果如图2所示.

由图2分析可知，和随机抽样法相比，独立特征选择法的RI值在8个数据集上都比前者要高.所以可以得出相对随机抽样而言，独立特征选择法用于聚类集成时的效果也比前者好.

使用独立特征选择法时，第一步要计算数据集中各个特征的相关性，然后按照数值的大小对特征进行排序，之后从中选取k个特征，这里k的取值经过后续实验得出为总特征的70%-80%为最佳，无论数据集特征的多少，我们是按照百分比抽取相关性最小的特征，这与数据集特征的多少是无关的，在图2的实验中也有验证.其中Sonar与CNAE-9为高维数据集(特征多)，其余数据集属于低维数据集(特征少).

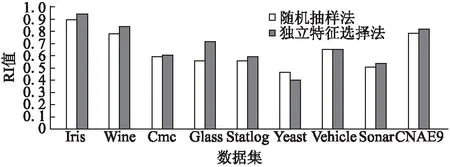
图2 两种数据子集选择算法的对比Fig.2 Comparison of two data subset selection methods

使用独立特征选择法时，需要为数据子集选择k个特征，为了确定数据子集中k的取值范围，本文分别给k取特征总数的10%，20%，30%，40%，50%，60%，70%，80%，90%，100%作为新的特征进行实验，以RI值为依据，观察 取不同值时对RI值产生的影响，划定k的范围.因为要对k分别取值，所以特征总数不能太少，我们取表1中特征数大于10的数据集进行实验，所选数据集见表3.

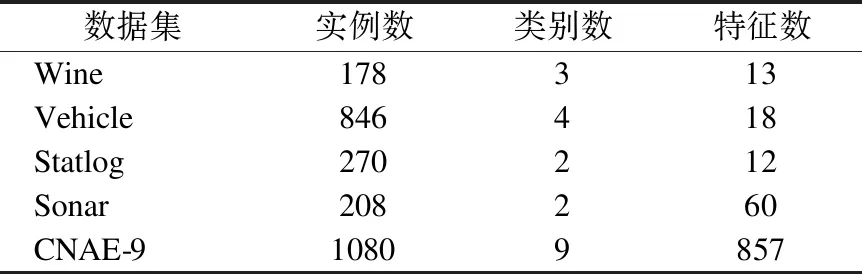
表3 确定k范围所用数据集Table 3 Determine the data set used for the k range

分别使用7种聚类集成算法在表3的数据集中进行实验，得到的结果如图3-图7所示.

075070065060055050045.......RI值02.04.06.08.10.k和总特征数的比值EACCSPAHGPAMCLAGKPCHCSSCEBMLF图3 Wine下RI值图4 Vehicle下RI值图5 Statlog下RI值Fig.3 RIvalueunderWineFig.4 RIvalueunderVehicleFig.5 RIvalueunderStatlog

图3-图7中每一条折线代表一种聚类集成算法，当取到特征总数的70%-80%时，大部分聚类集成算法获得的RI值都是最高的.说明数据子集中的取值范围在总体特征个数的70%-80%时为最佳.

实验在表2的数据集上进行，将本文的CEBMLF算法与EAC[3]、CSPA[1]、HGPA[1]、MCLA[1]、GKPC[16]、HCSS[17]这6种聚类集成算法进行对比.得到结果并计算它们的RI值，实验结果见表4，最好的结果加亮显示.

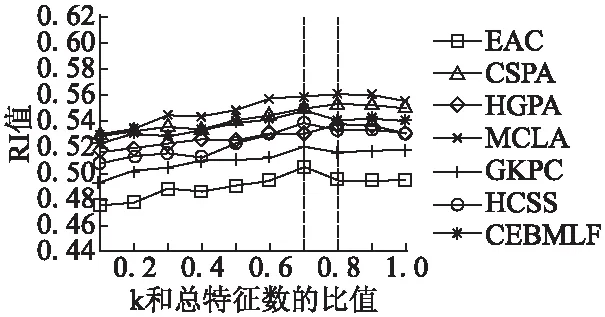
图6 Sonar下RI值Fig.6 RI value under Sonar

图7 CNAE-9下RI值Fig.7 RI value under CNAE-9

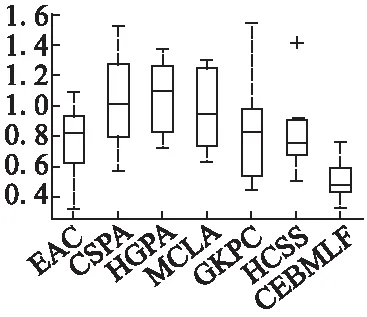
图8 各种算法的结果变化幅度比较Fig.8 Comparison of the results of various methods

由表4分析可知，CEBMLF算法在7个数据集上获得了最高的RI值，在剩下的数据集上也获得了较好的结果(为第二位)且与最好结果相差不到1%.说明CEBMLF算法聚类集成的准确率高.

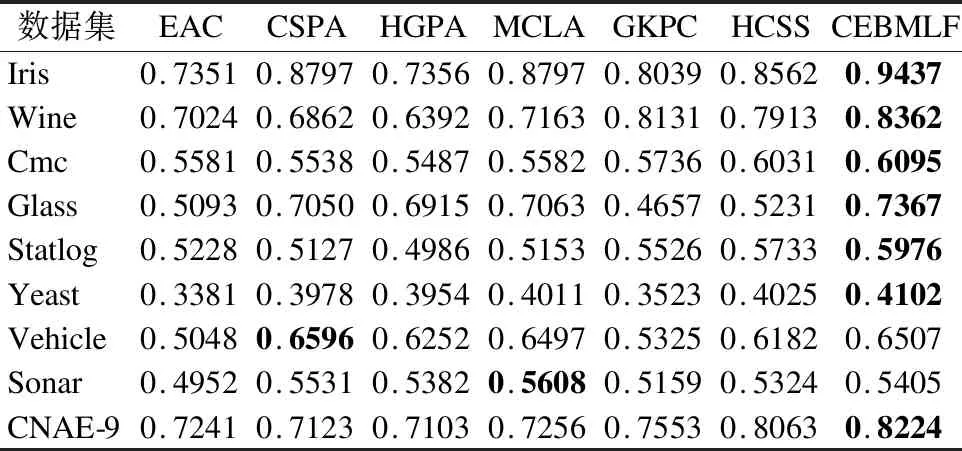
表4 各种算法的RI值Table 4 RI values of various algorithms

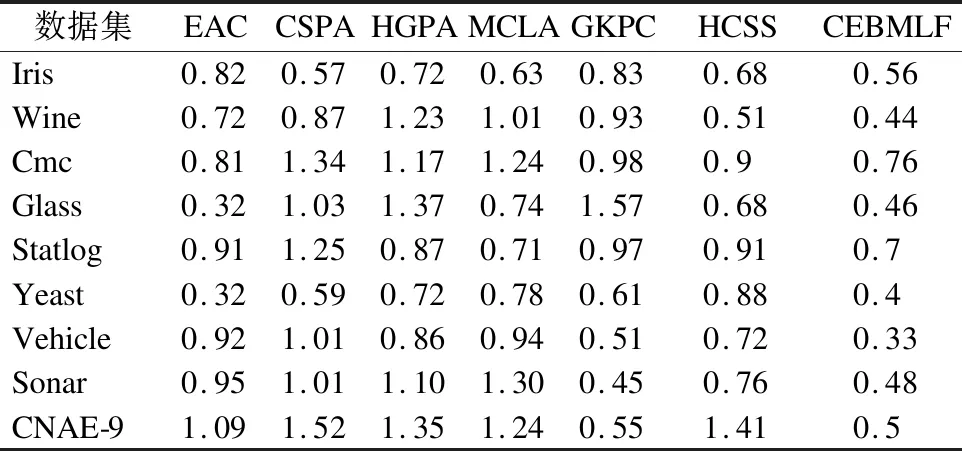
表5 各种算法的标准差(%)Table 5 Standard deviation of various algorithms (%)

然后计算7种集成算法在表2中9种数据集上的标准差.见表5.通过表5可以看出本文提出的CEBMLF算法较其余6种聚类集成算法相对稳定.也可以通过图8直接观察，在图中，CEBMLF算法位于7种算法的最底端，而且上下限的范围相对较小，得出CEBMLF算法的结果变化幅度相对其余算法较小，比较稳定.

5 结 论

本文提出了一种基于多链接特征子集的聚类集成算法.该算法为了得到准确率更高的聚类集成结果，在基聚类结果的生成阶段使用了特征子集和多种不同的聚类算法，通过独立特征选择法选出独立的特征子集作为多种不同聚类算法的输入，然后将数据点与簇的相关性集成信息矩阵转化为数据点之间的相关性关系矩阵，融合基聚类结果的关系矩阵，对融合的关系矩阵使用Average-Linkage算法进行聚类，得到最终结果.通过实验结果表明该算法能使最终聚类的准确率得到提升.