网络化控制系统的非脆弱H∞控制
张 磊,王思明
(兰州交通大学 自动化与电气工程学院,兰州 730070)E-mail:403797195@qq.com
1 引 言
网络化控制系统NCSs(networked control systems)是一种在各个节点(传感器与控制器以及控制器与执行器)之间使用网络进行数据传输的闭环反馈的控制系统[1].将通信网络引入控制回路中会产生新的问题.由于网络带宽的限制,资源竞争等现象,网络时滞现象在数据传输是无法避免的,网络时滞会使系统的控制性能变低,严重的会导致系统失稳[2].通信网络因其传输链路的不稳定,易受到干扰以及发生数据拥塞现象,会导致在传输过程中产生数据丢失[3,4].
在该类系统中,存在一些限制,其中最主要的是实际物理环境的限制,如测量仪器分辨率、有限字长以及数模转换[5].上述限制会使控制器存在参数摄动,会使闭环系统性能下降,更甚者会使系统无法稳定.非脆弱控制[6]就是设计控制器针对自身参数摄动引起系统性能下降问题的不敏感或者非脆弱.近些年来,网络化非脆弱控制问题得到了国内外许多的关注.文献[7]将马尔可夫跳变引入网络化控制,同时将采样周期等于网络时滞,且时延服从马尔可夫链,最后设计了具有非脆弱的保性能控制器.文献[8,9]设计了的非脆弱保性能控制器和非脆弱H∞保性能控制器.其网络化线性控制系统具有少于一个采样周期的网络诱导延时.文献[10]针对网络化线性系统中具有丢包和时延的问题,应用时滞系统方法,进行非脆弱的保性能控制器.文献[11]在文献[10]的基础上设计了其容错控制器.文献[12]针对网络化线性系统,设计了具有量化和区间时滞的非脆弱H∞控制器.文献[13]针对时滞网络化非线性系统,设计了非脆弱保性能控制问题和非脆弱保性能H∞控制问题,其系统为具有长时延网络化Lipschitz非线性系统的.文献[14]采用Lyapunov函数方法研究了网络化切换的模糊时滞系统,并研究了其非脆弱状态反馈控制问题.本文考虑网络诱导时延、数据丢包以及控制器参数摄动等问题对系统的影响,设计了能使系统稳定的非脆弱控制器,使得被控系统能满足H∞的性能指标.
2 问题描述
将被控系统考虑为线性离散时不变系统,如式(1)所示:

(1)
式中,x(k)∈Rn,u(k)∈Rm,w(k)∈Rp,z(k)∈Rq分别为系统状态、控制输入、外部扰动输入和被调输出;A,B1,B2,C,D为合适维数的矩阵[15].
由于网络化控制系统中通信网络自身特性,丢包现象在系统中时有发生,使用马尔可夫链来描述丢包过程.用下列矩阵来描述状态转移概率矩阵:

当σ(k)=0时,表示数据未丢包;σ(k)=1时,表示数据丢包[18].
当σ(k)=0时,数据在网络上传输时将会不可避免地产生网络诱导时延,定义时延为d(k),则控制器端的状态为式(2)和式(3)所示:
x(k)=x(k-d(k))
(2)
0≤d(k)≤d2
(3)
d2为非负整数时滞d(k)的上限.
下式为非脆弱加性状态反馈控制器:
u(k)=(K+ΔK)x(k-d(k))
(4)
其中K为增益矩阵;ΔK表示增益摄动矩阵,ΔK=HF(k)E;不确定矩阵F(k)FT(k)≤I.其中,H和E是具有特定维数的常数矩阵,F(k)是未知的实值时变矩阵[16].
于是,得到闭环离散控制系统式(5):

(5)
当σ(k)=1时,控制器接收不到网络传来的数据,此时采用前一时刻的值,即:
u(k)=u(k-1)=(K+ΔK)x((k-1)-d(k-1))
则网络化控制系统可描述为式(6):

(6)
综合式(5)和式(6),网络控制系统可以描述为马尔可夫跳变系统.如式(7)所示:
(7)
其中:Ad=B1(K+ΔK).
定义一个新的变量如式(8)所示:
y(k)=x(k+1)-x(k)
(8)
由式(6)和式(7)可得式(9):
y(k)=(A-I)x(k)+Adx((k-i)-d(k-i))+B2w(k)i=0,1
(9)
3 稳定性分析
定理1.对给定的常数d2,若存在适当维数的矩阵P>0,Q1>0,R1>0使得如下式(10)成立,那么满足式(10)的系统在控制器作用下式(7)渐近稳定.
(10)
式中:
Γ=ATPA-P+Q1+(A-I)TΘ(A-I)-R1
Γ1=ATPAd+(A-I)TΘAd
Γ3=-Q1-R1
AT表示矩阵A的转置矩阵,*表示矩阵中对称位置元素的转置矩阵.
引理1.[17](Jensen不等式)对给定的常数d>0,正定对称矩阵R>0和函数x(k),y(k)k=(1,2,…),其中x(k),y(k)满足y(k)=x(k+1)-x(k),可得如式(11)所示的不等式成立:

(11)
引理2.[18]给定具有适当维数的矩阵Q=QT,H,E,则
Q+HF(k)E+ETFT(k)HT<0
对所有满足F(k)FT(k)≤I的F(k)都成立的充要条件是存在一个正数ε>0使得式(12)成立:
Q+ε-1HHT+εETE<0
(12)
式(12)等价于式(13):
(13)
引理3.[19]对于两个矩阵Z∈Rn*m,G∈Rn*m,以及对称矩阵P∈Rn*n,有-GTP-1G≤ZTPZ-GTZ-ZTG,当且仅当Z=P-1G时等号成立.
设w(k)=0,当i=0时式(9)可化为如式(14)所示:
y(k)=(A-I)x(k)+Adx(k-d(k))
(14)
证明:构造如下形式的Lyapunov-Krasovskii函数:
其中:
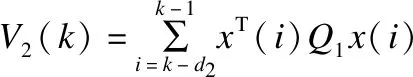
对以上三式求其前项差分ΔVi=Vi(k+1)-Vi(k),i=1,2,3,并结合引理2可知:
ΔV1(k)=xT(k+1)Px(k+1)-xT(k)Px(k)
=xT(k)(ATPA-P)x(k)+2xT(k)ATPAdx
ΔV2(k)=xT(k)Q1x(k)-xT(k-d2)Q1x(k-d2)

综合式ΔV1,ΔV2,ΔV3,可得:
ΔV(k)=ΔV1+ΔV2+ΔV3
≤xT(k)[ATPA-P+Q1+(A-I)TΘ(A-I)]x(k)+
式中:
ζT(k)=[xT(k)xT(k-d(k))xT(k-d2)]
由矩阵不等式(10)可得如式(15)的矩阵不等式:
Φ<0
(15)
证明完毕,同理可以证明w(k)=0,i=1时系统渐进稳定.
定理2.对于给定的非负整数d2,若存在具有合适维数的矩阵P>0,Q1>0,R1>0和标量ε>0,使得如式(16)成立,则系统式(7)在有任意允许的参数不确定性的控制器的作用下渐进稳定.
(16)
其中:
M1=-P+Q1-R1
M2=-Q1-R1
M3=ATP
M4=d2(A-I)TR1
M5=(B1K)TP
M6=d2(B1K)TR1
证明:对于式(13),由Schur补定理容易得到系统渐近稳定条件,如式(17)所示:
(17)
将上面式子中的Ad用B1(K+HF(k)E)来代替,容易得到如(18)所示的式子:
(18)
其中:
Φ1=B1(K+HF(k)E)T
Φ2=d2B1(K+HF(k)E)T
式(18)可以表示成如下式(19)
(19)
其中:
X1=[0 0 0HTd2HT]T
Y1=[0E0 0 0]
由引理2可知,必然存在一个正数ε>0使得下面的式(20)成立:
(20)
由引理(3)可知,式(20)等价于式(21):
(21)
证明完毕.
同理可以证明w(k)=0,i=1时系统渐进稳定.
定义1.考虑如式(7)的离散时延系统,对于给定的正常数γ,如果系统具有以下性质:
1)系统可以达到渐近稳定.
2)在零初始条件x(k)=0下具有给定的H∞扰动抑制水平γ>0,则称系统(7)具有H∞性能γ.有:
‖z‖2≤γ‖w‖2,∀w∈L2[0,∞)

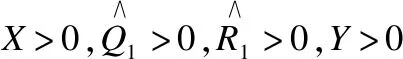
(22)
证明:在零初始条件下,系统式(7)具有给定的H∞扰动抑制水平γ.对于任意w(k)∈L2[0,∞)有:
V(k+1)-V(k)+zT(k)z(k)-γ2wT(k)w(k)<0
进一步可以得到:
由于闭环系统是渐进稳定的,所以有:
满足所描述的H∞性能要求,进而可知:
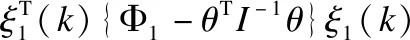
其中:
此时ξ1(k)作为表征4个状态变量的矩阵,即:

(23)
式中:
将式(23)中的Ad用B1(K+HF(k)E)来代替,可以表示成如式(24)所示.
(24)
其中:
X1=[0 0 0 0HTd2HTHT]T
Y1=[0E0 0 0 0 0]
由引理2可知,必然存在一个正数ε1>0使得下面的式子成立:
(25)
式(25)等价于:
(26)
同理可以证明i=1时系统不仅渐进稳定,而且在零初始条件下具有给定的H∞扰动抑制水平γ.定义1得证.
4 仿真分析
为了验证本方法的有效性,给出了仿真示例.考虑式(7)的网络化控制系统,参数如下所示:
1)不存在扰动时,A的特征值为2,1,未达到稳定系统的状态响应如图1所示.
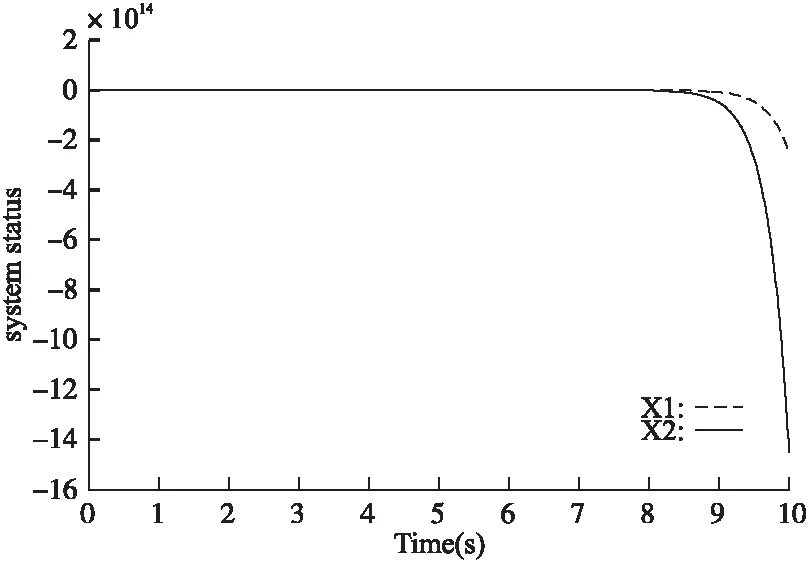
图1 开环系统状态响应Fig.1 Open loop system status response
在上述控制器的作用下,被控系统的闭环状态响应如图2所示.

图2 有扰动时非脆弱控制器的闭环状态响应Fig.2 Closed-loop state response of non-fragile controllers with disturbances
从图2可以得到,考虑到控制器的扰动以及参数摄动的,本文设计的非脆弱控制器可以实现网络化控制系统的稳定性,并且使网络化控制系统满足H∞性能指标,验证了方法的可行性.

图3 扰动w(k)随机数列Fig.3 Disturbancew(k)random sequence
5 结 论
本文针对网络控制系统中网络时滞、丢包和控制器参数摄动等问题.分析网络控制系统,使用李雅普诺夫稳定理论得到控制器的充分必要条件以及矩阵增益K.上述问题得到有效的解决,系统渐近稳定,满足H∞性能指标γ.由仿真结果表明,设计的控制器能满足系统H∞的性能指标,同时也可以使系统达到渐进稳定.

