三维属性拓扑的衰减特性分析
张 涛,刘梦奇,荣 美
(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)E-mail:zhtao@ysu.edu.cn
1 引 言
形式概念分析是一种对形式背景进行数据分析和规则提取的重要工具,目前,国内外学者对形式概念分析的关注度越来越高且已经成功应用于数据分析[1]、机器学习[2]、知识发现[3]、软件工程[4]等领域.基于形式概念分析的认知研究也是本领域的重要方向[5],并取得了一定成果.
属性拓扑(Attribute Topology)[6,7]是近年来形式概念分析领域出现的一种新型形式背景的直观表示方法,属性对象间用基本二元关系表示,构建与形式背景对应的属性关联拓扑网络,以属性为顶点,属性对间的包含关系为权值,以加权图的形式对形式背景进行刻画,将属性间的耦合关系和耦合强度直观的表现在拓扑图上[8,9].属性拓扑在概念计算[10,11]、关联关系发现[12]、因果分析[13]、认知模型构建[14,15]等领域都已有所发展.
但目前属性拓扑的表示是二维的,二维平面的属性拓扑对于属性强度的描述存在局限性.二维属性拓扑注重刻画属性结点和结点之间的关系,但是缺乏对属性结点本身的描述,对属性结点的强度表示不突出.因此,本文提出三维属性拓扑的概念,同时对三维属性拓扑的衰减特性进行了分析和证明,并将其应用于对人脑遗忘特性的可视化分析.
2 属性拓扑的基本概念
形式背景是形式概念分析的基本表示方法,其定义如下.
定义1[16].一个形式背景表示为K=(G,M,I),其中,G表示形式背景中所有对象的集合,M表示形式背景中所有属性的集合,I⊆G×M表示对象与属性之间的关系.(g,m)∈I或gIm表示对象g具有属性m.
属性拓扑是一种新型的具有可视性的形式背景表示方法,通过对属性之间的二元关系的表示,构成网络拓扑结构.为了更好地表示形式背景中属性对间的各种关联关系,现给出如下属性拓扑相关定义:
定义2.形式背景K=(G,M,I),∀mi,mj∈M且mi≠mj,形式背景K的属性拓扑表示为AT=(V,Edge),其中V=M是属性拓扑中的顶点集合,Edge是属性拓扑边的权重,Edge表示为:
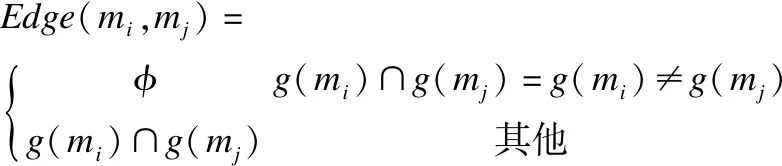
(1)
3 三维属性拓扑
通过以上分析可知,二维属性拓扑可以对形式背景进行直观地表示,但是现有的二维属性拓扑无法表示属性强度关系,为了描述各属性的强度关系,现提出三维属性拓扑的概念.
3.1 三维属性拓扑的概念
首先给出与三维属性拓扑相关的基础定义.
定义3.在属性拓扑AT=(V,Edge)中,∀mi,mj∈V且mi≠mj,属性结点mi和mj间的相互依赖度Ix(mi,mj)为:
(2)
其中,g(mi)∩g(mj)表示mi与mj分别所属对象集的交集,g(mi)表示mi所属对象集,g(mj)表示mj所属对象集,#(·)表示求集合·的大小.
定理1.相互依赖度Ix(mi,mj)和相互依赖度Ix(mj,mi)大小相等,即Ix(mi,mj)=Ix(mj,mi).
证明:
定义4.属性强度:已知形式背景K=(G,M,I),对应属性拓扑AT=(V,Edge),∀mi,mj∈V且mi≠mj,属性结点mj对应的相互依赖度Ix(m1,mj),Ix(m2,mj),…,Ix(mN,mj)的总和称为属性强度,表示为:
(3)
N为含属性结点mj的属性相互依赖度中,使得Ix(mi,mj)≠0的mi结点的个数.
定义5.已知属性拓扑AT=(V,Edge),∀mj∈V,属性拓扑中所有属性强度的平均值称为强度半径,表示为:
(4)

对于二维属性拓扑AT=(V,Edge),加入属性强度,构成具有强度值的三维属性拓扑,现给出如下三维属性拓扑的定义.
定义6.形式背景K=(G,M,I),∀mi,mj∈M且mi≠mj,形式背景K的三维属性拓扑表示为AT=(V,Edge,Iv),其中V=M是属性拓扑中的顶点集合,Edge是属性拓扑边的权重,Edge表示为:
(5)
Iv是各个顶点的强度集,Iv表示为:
Iv={I(m1),I(m2),…,I(mj),…,I(mn)}
(6)
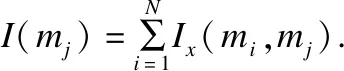
属性强度的加入,使原有二维属性拓扑结构层级化,加入强度特性的三维属性拓扑与传统二维属性拓扑的模型对比图如图1所示,图1(a)为二维属性拓扑模型,图1(b)为三维属性拓扑模型,其中,纵轴表示属性强度.通过比较图1(a)二维属性拓扑模型和图1(b)三维属性拓扑模型可以看出,二维属性拓扑的各属性位于同一平面,而三维属性拓扑中,由于各属性的强度不同,属性呈现在不同的平面,强度大的属性位于强度小的属性的上层.

图1 二维属性拓扑与三维属性拓扑对比模型图Fig.1 Comparison model diagrams between two-dimensional attribute topology and three-dimensional attribute topology
由二维属性拓扑及三维属性拓扑的定义,性质1显然成立.
性质1.二维属性拓扑AT=(V,Edge)为三维属性拓扑AT=(V,Edge,Iv)在xOy平面的投影.
3.2 三维属性拓扑的衰减特性
3.2.1 时间特性下三维属性拓扑强度分析
三维属性拓扑的衰减特性体现在不同强度的属性位于不同的强度层级.随着时间的流逝,属性进行衰减并分层.在三维属性拓扑AT=(V,Edge,Iv)的基础上加入时间特性,表示为:ATt=(Vt,Edget,Iv).
加入时间特性的三维属性拓扑ATt使原三维属性拓扑AT的强度特性会随着时间发生变化,同时,三维属性拓扑中的属性分为不同的层级,三维属性拓扑中的分层表示模型如图2所示.

图2 三维属性拓扑分层表示模型Fig.2 Three-dimensional attribute topology hierarchical representation model
本文中,考虑四个层级,四个层级代表四个不同的强度,分别为初始层Layerori、一级衰减层Layerfir、二级衰减层Layersec和三级衰减层Layerthi.其中,初始层中包含原始三维属性拓扑中的所有属性.
属性在衰减过程中,属性强度产生变化,变化是通过对不同层级的属性进行加权处理得到的,现给出衰减系数的定义,用来分析属性强度的变化.
定义7.衰减系数χ(Layerl)与时间t的关系满足:
χ(Layerl)=λt
(7)
0<λ<1,χ(Layerl)即l层的衰减系数.
属性初始的状态为全部属性位于同一层级,此时属性拓扑中的强度层级总数L=1,L表示强度级数总数.
定义8.层级属性强度:当强度层级总数L>1时,三维属性拓扑AT=(V,Edge,Iv),mi∈V,属性结点mj层级属性强度表示为:
(8)
其中,p为l层中使得Ix(mi,mj)≠0的属性结点mi个数,q为l+1层中使得I(mi,mj)≠0的属性结点mi个数,χ(Layer|mi)表示mi所在强度层级中的衰减系数.
当强度层级总数L>1时,各层属性强度平均值在该层单独计算,有如下定义:
定义9.三维属性拓扑AT=(V,Edge,Iv)中,mi∈V且mi∈{∧Layerl},当强度层级总数L>1时,层级属性强度半径为在位于本层中属性的属性强度的平均值,表示为:
(9)

在不同时刻t0,t1,t2,t3下,对应的属性拓扑分别为:
ATt0=(Vt0,Edget0,Iv),ATt1=(Vt1,Edget1,Iv)
ATt2=(Vt2,Edget2,Iv),ATt3=(Vt3,Edget3,Iv)
不同时刻的层级分布示意图如图3所示.
3.2.2 三维属性拓扑的层级衰减
根据对三维属性拓扑中属性强度特性和时间特性的分析,随着时间的流逝,不同强度的属性分布于不同的强度层级,三维属性拓扑会呈现动态的结构变化.

图3 属性层级分布示意图Fig.3 Attribute hierarchy distribution diagram
对于原始三维属性拓扑AT=(V,Edge,Iv),∀mi∈V,mi∈{∧Layerori},其中{∧Layerori}表示位于初始层的属性集合.对当前强度层级的属性强度和强度半径进行大小对比,依此判定某属性在下一个时刻发生的层级变化情况,判定依据如以下分层运算规则所示:
三维属性拓扑AT=(V,Edge,Iv),∀mi∈V,若:


由分层运算规则可知,tn时刻某强度层级的属性及其所处层级在tn+1时刻有两种去向,一种在tn+1时刻仍处于该层,另一种下降一个层级,下面对属性的两种去向进行分析.
1)设属性强度层级在tn~tn+1(n=0,1,2,3)时间内平移过程表示为:


2)设属性强度层级在tn~tn+1(n=0,1,2,3)时间内下降过程表示为:

其中,l+1层为l层降低一层后的层级,{∧Layerl|mi↓}tn表示tn时刻l层属性mi强度层级下降的属性集合,{∧Layerl+1}tn+1表示tn+1时刻l+1层属性集合,得到tn+1时刻,{∧Layerl|mi↓}tn⊆{∧Layerl+1}tn+1.

证明:该性质易由分层运算规则证明.


□
性质4.{∧Layerl}tn∩{∧Layerk}tn=φ,k≠l.

□
衰减分层流程图如图4所示.

图4 衰减分层流程图Fig.4 Attenuation hierarchical flowchart
不同时刻属性分层情况不同,经过如图4所示属性衰减过程后,属性强度在衰减过程中发生变化,二维平面的属性拓扑呈现三维结构,更新为三维属性拓扑.随着时间的流逝,属性强度发生改变同时属性层级结构也随之发生改变.
4 三维属性拓扑在遗忘分析中的应用
认知科学的研究认为,人脑的记忆和遗忘是相辅相成的,所有的信息在神经系统出发后都会进入遗忘过程[17].遗忘是衰减的一种表现形式,同时,属性拓扑在遗忘过程中存在遗忘模型,因此本文以人脑遗忘为例对三维属性拓扑的衰减特性进行分析表示.
4.1 数据选取与处理
为了验证三维属性拓扑对遗忘分析的可行性,本文选取心理学记忆与遗忘的例子作为样本,从人脑遗忘的数据角度进行分析,通过实验对其进行分析验证.
首先选取实验的被试者,被试者为燕山大学本科生、研究生共65人(其中男生28人,女生37人),平均年龄23.84岁,视力或矫正视力正常.其次,根据《现代汉语常用词频词典(音序部分)》选取中等频率双字名词[18]共8个词,包括:白色、棉花、柔软、土壤、温暖、信封、触摸和纯朴.
实验开始,被试者观看写有以上8个词语的卡片并记忆,随后收回卡片,记录不同被试者对8个词语的记忆程度,记忆程度以记忆系统中记忆值[19]来评估.此时取t0=0,为被试者记忆的初始结果,并将其详细记录.由于数据庞大,为描述简便,如表1所示随机选取8位被试者原始数据进行分析,并将所有数据中大于或等于平均值的词语所对应的记忆值赋值为1,否则赋值为0,得到经过二值化处理后的数据如表2所示.
4.2 实验结果与分析
对原始属性拓扑进行以天为单位的属性遗忘分析,令t0=0,t1=1,t2=2,t3=3,本实验中取λ=0.5.由公式(7)求得各时刻各层级的衰减系数,根据公式(2)~公式(4)求得各词语的属性强度及强度半径,并根据分层运算规则得到各个时刻词语的状态变化情况.
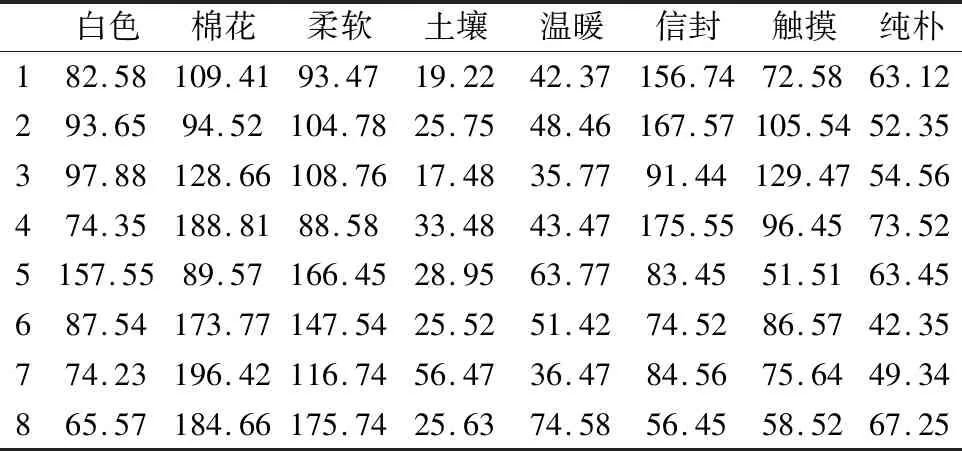
表1 部分原始数据Table 1 Partial raw data

表2 处理后的部分原始数据Table 2 Partial data after processing
t0=0时有且仅有一个初始层级,“白色”、“棉花”、“柔软”、“土壤”、“温暖”、“信封”、“触摸”和“纯朴”均位于初始层;t1=1时刻“白色”、“棉花”、“柔软”、“信封”和“触摸”保持在初始层不变,“土壤”、“温暖”和“纯朴”下降到一级衰减层,;t2=2时刻“白色”、“棉花”、“信封”保持在初始层不变,“柔软”、 “触摸”、 “温暖”位于一级衰减层,“土壤”、 “纯朴”下降到二级衰减层;t3=3时刻“白色”、“棉花”保持在初始层不变,“信封”、“触摸”位于一级衰减层,“纯朴” 、“柔软”、“温暖”位于二级衰减层,“土壤”下降到三级衰减层.不同时刻各个词语的各项数据及状态变化如表3~表6所示.

表3 t0=0时刻词语状态Table 3 Word status at t0=0
经过从初始状态到t3=3时刻的衰减,三维属性拓扑更新为四个强度层级,整个衰减过程强度层级分布图如图5所示.
对65位被试者在3天之后对8个词语的记忆情况进行统计,由于篇幅所限,65位被试者经过3天记忆衰减后记忆值汇总表格过大,表7只列出了表1中8位被试者的记忆值.

表4 t1=1时刻词语状态Table 4 Word status at time t1=1

表5 t2=2时刻词语状态Table 5 Word status at time t2=2
对65位被试者遗忘后记忆值计算其平均值,得到如表8所示结果,为了方便此结果与三维属性拓扑衰减结果的对比分析,需要对表6中三维属性拓扑衰减的强度值进行处理,对其增加两个数量级,以将强度值调整到合适范围,得到图6所示对比结果,其中灰色柱体表示为全部被试者对各个词语的记忆平均值,黑色柱体则表示通过三维属性拓扑衰减方法得到的记忆强度值调整数量级后的数值.

表6 t3=3时刻词语状态Table 6 Word status at time t3=3

图5 衰减过程强度层级分布Fig.5 Strength level distribution of attenuation process
通过图6中心理学的记忆与遗忘实验得到的记忆值和使用三维属性拓扑衰减方法所得数据的对比分析,可以看出,两组记忆结果在整体变化上呈现大致相同的趋势,且单个词语的记忆分析也趋向相同,如词语“棉花”在两组结果中均为记忆最强者,词语“土壤”均为记忆最弱者.由于未考虑个体差异,导致实验得到的结果与通过三维属性拓扑衰减方法得到的结果存在些许偏差,但是整体趋势基本吻合.
通过上述分析,可以看到人脑记忆随着时间的流逝呈现衰减状态.通过人脑遗忘特性对三维属性拓扑衰减进行直观表示,让遗忘可视化且有预见性,比如在学习中,对于易遗忘的知识做到重视,及时强化巩固,以提高学习效率.本文对于记忆实验得到的词语记忆结果仍具有片面性,如个体情绪、环境影响等因素,还需要结合更多的研究对象、记忆目标对象进行验证,因此有关大数据量的三维属性拓扑的衰减将是之后研究的方向之一.

表7 部分被试者记忆衰减后记忆值Table 7 Memory value of some subjects after memory attenuation

表8 全部被试者遗忘后记忆平均值Table 8 Average memory of all subjects after forgetting

图6 各词语遗忘后记忆平均值与三维属性拓扑衰减记忆强度对比Fig.6 Comparison of memory average and Three-dimensional attribute topological attenuation memory intensity after word forgetting
5 结 论
本文提出以三维属性拓扑为基础的衰减特性分析方法,根据属性强度对三维属性拓扑进行分层,从认知与记忆网络的角度说明其认知意义,并给出实验加以验证.通过人脑遗忘实验挖掘属性间的内在联系,并对实验数据进行整理和分析,实验结果表明,以三维属性拓扑为基础模拟人脑遗忘过程的方案具有可行性,三维属性拓扑的衰减基本符合人脑遗忘过程,同时,三维结构的衰减过程使遗忘过程可视化.
本文是对三维属性拓扑衰减特性的研究,探讨了三维属性拓扑的衰减特性,并结合属性遗忘与人脑认知的实际意义,为属性拓扑减量式结构分析提供一种思路和方法.

