求阴影部分面积的方法

◎徐洪梅

要求阴影部分的面积，首先要从整体上观察图形，看清图形的特征，其次还要善于挖掘题目中的隐蔽关系，发挥想象力，灵活、巧妙地进行解答。

1.等分法。在组合图形中，知道了整个图形的面积，要求阴影部分图形的面积，我们要先了解这些图形的特征，然后根据它们的特征用等分的方法来解决。

【例1】右图长方形的面积是160 平方厘米，点D、B分别是两边的中点，求阴影部分的面积。

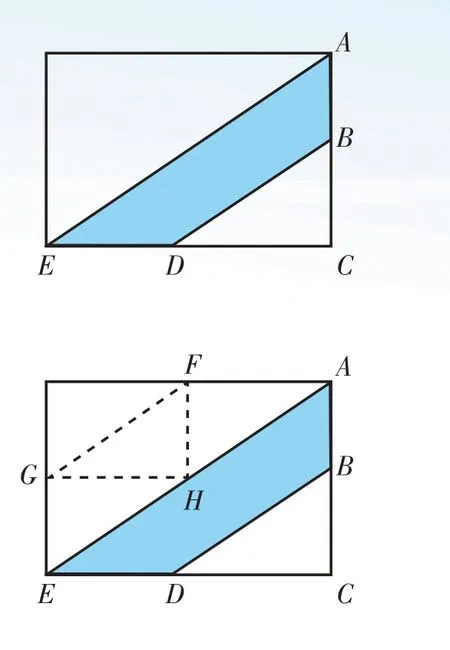
【分析与解】阴影部分是一个梯形，根据梯形面积的计算公式，需要知道上底、下底和高三个条件，但从题中无法求出这三个条件，因此需要转换思维视角，另辟蹊径。

由于点D、B 分别是两边的中点，可以想到运用长方形的对称性，把长方形进行等分。先取另外两边中点F、G，再将FH、FG、GH 连接起来（如右图），那么整个长方形就被平均分成8份，阴影部分占了其中的3 份。根据长方形的面积，就很容易求出阴影部分的面积了。

2.等量代换法。有些阴影部分的面积不能直接求出，我们可以采用转化的策略，通过等量代换求出结果。

【例2】如右图，两个完全一样的直角三角形重叠在一起，求阴影部分面积。（单位：厘米）

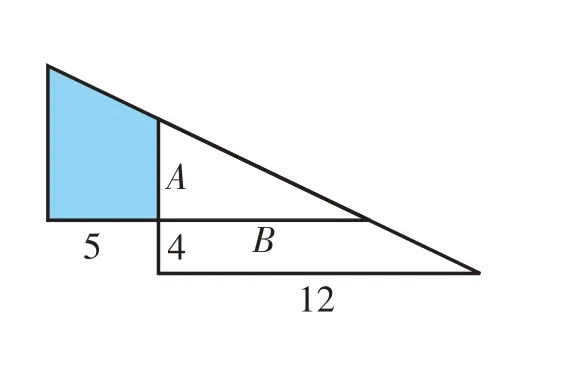
【分析与解】题中阴影部分虽然是个梯形，可是它的上底和下底都不知道，不能直接求出它的面积，阴影部分和三角形A 合在一起，就是原来的直角三角形，同时梯形B 和三角形A 合在一起，是与之完全一样的直角三角形。因此梯形B的面积就和阴影部分的面积一样大。

阴影部分面积为：（12-5+12）×4÷2=38（平方厘米）