对边简支功能梯度板振动功率流特性分析
吴江海, 朱竑祯, 安 方, 殷学文
(1. 中国船舶科学研究中心 船舶振动噪声重点实验室, 江苏 无锡214082; 2. 南京航空航天大学机械结构力学及控制国家重点实验室, 南京210016)
0 引 言
功能梯度材料(FGM)是一种新型复合材料,在微观上具有空间连续梯度变化的结构,可实现材料属性在结构剖面上的连续梯度变化。 与传统的层合材料相比,不同材料间的宏观界面被消除了,从而可以通过人为设计材料内部的梯度变化有效实现内力、温度等物理量沿厚度方向的渐变,达到缓解热应力[1]、避免或降低应力集中的目的。
目前大部分有关功能梯度材料结构力学特性的研究集中在热应力、弯曲、稳定性方面[2-5],而针对功能梯度材料结构的振动方面的研究也是比较热门的。曹志远[6]采用与矩形板边界条件相应的梁函数组合级数,求解得到适用于多种边界条件的功能梯度矩形板的固有频率与振型的解析解。 孙丹[7]等采用一阶剪切变形理论,由频散方程给出了波在功能梯度板中传播的频散及相速度曲线,分析了功能梯度材料指数对波传播的影响规律。 Singh 等[8]采用壳单元研究了功能梯度板壳的非线性振动和屈曲问题。黄小林[9]等基于Reddy 高阶剪切变形理论和广义Karman 型方程,用双重傅里叶级数展开法研究黏弹性地基上功能梯度材料板的自由和强迫振动特性,并讨论了材料组份、平板尺寸及地基参数对动态响应的影响。 关于功能梯度结构的振动问题研究大多仅仅考虑材料的梯度指数对于振动模态的影响,而很少以此为出发点进一步分析结构中的振动能量分布。
振动实际上是一种能量的传递,振动功率流就基于结构上的力和速度,反应结构中能量的传递,从能量的观点研究结构振动和噪声问题。 平板功率流的研究已经较为成熟,在1978 年Goyder[10]就引入功率流的概念,以此分析有限大平板和梁的弯曲波、扭转波以及功率流的传播。 Seo 等[11]采用波传播法求解了中高频域内含加强筋的平板振动响应,基于功率流研究了平板内的能量分布,尤其对板与梁组合界面上波的反射与功率流的传播做了详细的分析。 张雄等[12]基于薄板有限元模型,研究了不同边界条件下的薄板结构的振动功率流特性,并且绘制了功率流矢量场分布图,以此反应振动源的位置以及振动能量的分布特征。 大部分平板振动功率流的研究都是关于各向同性板的分析,而对于功能梯度板的研究较少。 华中科技大学的张玲等[13]基于四边简支矩形板的解析解,采用模态叠加法,得到了四边简支功能梯度矩形薄板的横向自由振动的位移, 结合振动功率流分析平板受简谐载荷时板内的功率流传播。
在弹性力学的经典理论中,对于矩形板的横向振动来说,除了四边简支的边界情况外,其余边界下矩形板的振动均没有解析解, 因此其振动问题是较难求解的。 有限元法可以突破对边界条件的约束,但由于其单位位移函数不精确,因此往往需要将结构细化为大量单元,降低了计算效率[14]。 动刚度法通过引入满足边界条件的精确位移假设,只需将结构划分为若干个单元,甚至一个单元便可进行精确求解[15]。 本文将动刚度法引入对边简支功能梯度矩形薄板的横向振动及动态响应求解,在此基础上研究功能梯度矩形板的振动功率流特性。
1 基于动刚度法的对边简支功能梯度矩形板面外振动
图1 中为一个矩形薄板,沿x 方向板长为b,沿y 方向板宽为L,厚度为h。假设y=0 和y=L 两条边简支,以“SSSS”表示,如图中所示,而x=0,x=b 两条边的边界条件可任意组合。 考虑薄板问题, 忽略剪切变形和转动惯量的影响, 满足Kirchhoff 假设。

图1 功能梯度板Fig.1 Functionally graded plates
沿厚度方向变参数的功能梯度矩形板的面外自由振动方程为

考虑阻尼的影响,用EC=E (1+ jη )代替原杨氏模量。 因此振动方程(1)简化为

本文考虑简谐激励下的振动,则力和位移为随时间t 呈简谐变化的函数,考虑到y=0 和y=L 两条边简支,因此将(2)式的解设为



将x=0 和x=b 两边界上的位移向量和力向量表示为:



其中的下标m 表示第m 项项数。
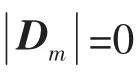
2 功能梯度板振动功率流
功率流是单位时间内所做的功。 假设作用于结构某处的激励瞬时值为P(t ),相应的速度响应为V(t ),此时的瞬时输入功率流值为P(t )=F(t )V(t ),而在工程中,在一段时间内的平均功率流比瞬时功率流更方便,因此有

对于简谐激励,外力与速度响应可写为:F(t )=Feiωt,V(t )=Veiωt,从而输入功率流为P=Re (F· V*)。能量输入板结构后,会在板内传播,单位时间内传播的能量即为传播功率流。 对于板上的每个点,有2个微元面垂直x 轴和y 轴,求出这两个微元面上的功率流即可得该点的功率流矢量。 矢量模的大小为功率流大小,方向为能量传播方向。 基于Kirchoff 假设的薄板的功率流强度表达式为:

式中:Qx和Qy为横向剪力,Mxx和Myy为弯矩,Myx和Mxy为扭矩。 由上一节中, 施加外力后得到结构的响应,求得结构位移,结合内力函数一起代入(8)式,即可求得功率流。
3 算例分析
3.1 功能梯度矩形板模态分析
本文取文献中的功能梯度矩形板模型,考虑板x 方向为1 m,y 方向为0.8 m,厚h=0.01 m,弹性模量与密度沿厚度方向以幂指数规律变化,泊松比、温度不变。参考文献中考虑为陶瓷-金属功能梯度矩形板,其材料属性按如下规律变化:

式中:Xm、Xc为金属和陶瓷的材料属性,k 为梯度指数(下文中不加特别说明时,梯度指数k 值取1)。 考虑Al/Al2O3功能梯度材料,则弹性模量Em=70 GPa,Ec=380 GPa,密度为ρm=2 707 kg/m3和ρc=3 800 kg/m3,泊松比νm=νc=0.3,结构阻尼η=0.001。
本文首先给出了功能梯度矩形板三种边界下前八阶固有频率,四边中有两条为简支边界,故考虑另外两条边为固支、简支、自由三种边界条件。其中四边简支板在文献[1]中给出了经典解,本文同时采用了ABAQUS 有限元进行了三种边界条件的下模态分析,将两者与本文级数解析解进行对比分析。可以看出本文与文献中的经典解吻合较好,文献与本文的解均基于薄板理论基础,而有限元中的解考虑剪切变形,故两者存在一定的误差。 本文与有限元的误差较小,三种边界条件中最大误差为3.6%,优于文献[13]中的最大误差7.98%,说明本文中的方法均有较高的精确度。

表1 功能梯度矩形板固有频率(Hz)Tab.1 Natural frequencies of an FGM rectangular plate (Hz)
表2 中给出了三种边界条件下,不同梯度指数下功能梯度矩形板的前八阶固有频率。 从表中可以明显地看出每种边界条件下,随着梯度指数增大,功能梯度板刚度增大,各阶固有频率值增大。 两边固支板的固有频率最大,两边简支次之,两边自由为最小。

表2 不同梯度指数功能梯度板固有频率(Hz)Tab.2 Natural frequencies of an FGM plate with different graded indexes (Hz)
3.2 功能梯度矩形板输入功率流分析
本文中作用力大小为1 N,作用点为板中心(0 m,0.4 m)处。 根据输入功率流的公式,计算四边简支条件下功能梯度板的输入功率流,并将其无量纲化,如图2。 从输入功率流曲线可以看出,输入功率流的大小与激励频率相关, 在某些频率附近出现峰值,这些峰值频率分别与功能梯度板的固有频率对应。前三个峰值为101 Hz、417 Hz 和595 Hz,从功能梯度板对应振型中看出,由于矩形板的对称性,在奇数阶模态下,板中点的速度最大,在偶数对称模态中,中心点为振型节点,故输入功率流在奇数模态时出现峰值。 其中LW=10lg (P/ P0),P0=1×10-12W。

图2 功能梯度板输入功率流Fig.2 The input power flow of an FGM plate
图3 给出了不同梯度指数下功能梯度板输入功率流随频率变化的曲线。 从图中可以看出,随着梯度指数的增大,输入功率流的峰值也相应地向高频移动,并且偏移量也随着频率的增大而增大。 这与表1 中不同梯度指数下功能梯度板的固有频率变化一致,板的固有频率增大,所以输入功率流的共振峰也向高频移动,梯度指数越大,板的刚度变化越快,固有频率变化也就越大,偏移量也因此变大。 但输入功率流幅值并没有变化, 说明在相同作用力下,板中心的振动速度幅值一致,该点的机械阻抗并没发生变化。

图3 功能梯度板输入功率流Fig.3 The input power flow of an FGM plate with different grade indexes
3.3 功能梯度矩形板功率流传播分析

图4 功能梯度板功率流矢量图Fig.4 The power flow vector of an FGM plate

图5 功能梯度板功率流流线图Fig.5 The power flow streamline of an FGM plate
基于上面动刚度法与功率流公式,本文计算了功能梯度板内功率流矢量图与流线图。 为了验证本文功率流计算的正确性,给出功能梯度板四边简支条件下在486 Hz 激励下功率流矢量图和流线图。 从图4 与图5 可以看出,本文的结果与文献中的经典解法、有限元解法的矢量图与流线图吻合,证明了本文方法的正确性。不同的边界条件影响平板的刚度,即影响板内功率流的传播方式。本文给出功能梯度板在486 Hz简谐激励下,两短边简支,另外两长边简支、固支、自由三种边界条件下板内的功率流传播矢量图与流线图,如图6-7。 考虑该算例板具有高度的对称性,本文给出矩形板的右半边结果。 从图中可以看出,三种边界条件可以明显地找出力作用点。 边界条件影响了板内能量涡的分布。 固支边界下,板内没有涡结构,能量从力作用点直接流向简支边。 简支边界下涡结构均匀且较大,而自由边界下涡结构较小且远离力作用点。
为了研究功能梯度板振动功率流特性,本文分别给出了四边简支边界条件下,在486 Hz 与912 Hz激励下,不同梯度指数情况下板内功率流流线图,如图8-9 所示。 从图中可以看出912 Hz 激励下板内出现了复杂的能量漩涡,但仍能清晰地识别出激励源位置,且流线图能较好地识别板内结构的能量传播路径。 随着指数的增大,板的刚度值变大,板内能量漩涡减小,能量沿单方向传递。
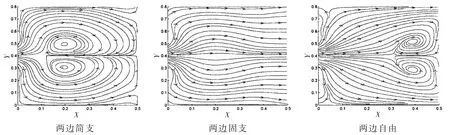
图6 不同边界条件下功能梯度板功率流流线图Fig.6 The power flow streamline of an FGM plate with different boundary conditions

图7 不同边界条件下功能梯度板功率流矢量图Fig.7 The power flow vector of an FGM plate with different boundary conditions

图8 不同梯度指数功能梯度板功率流流线图(486 Hz)Fig.8 The power flow streamline of an FGM plate with different graded indexes (486 Hz)
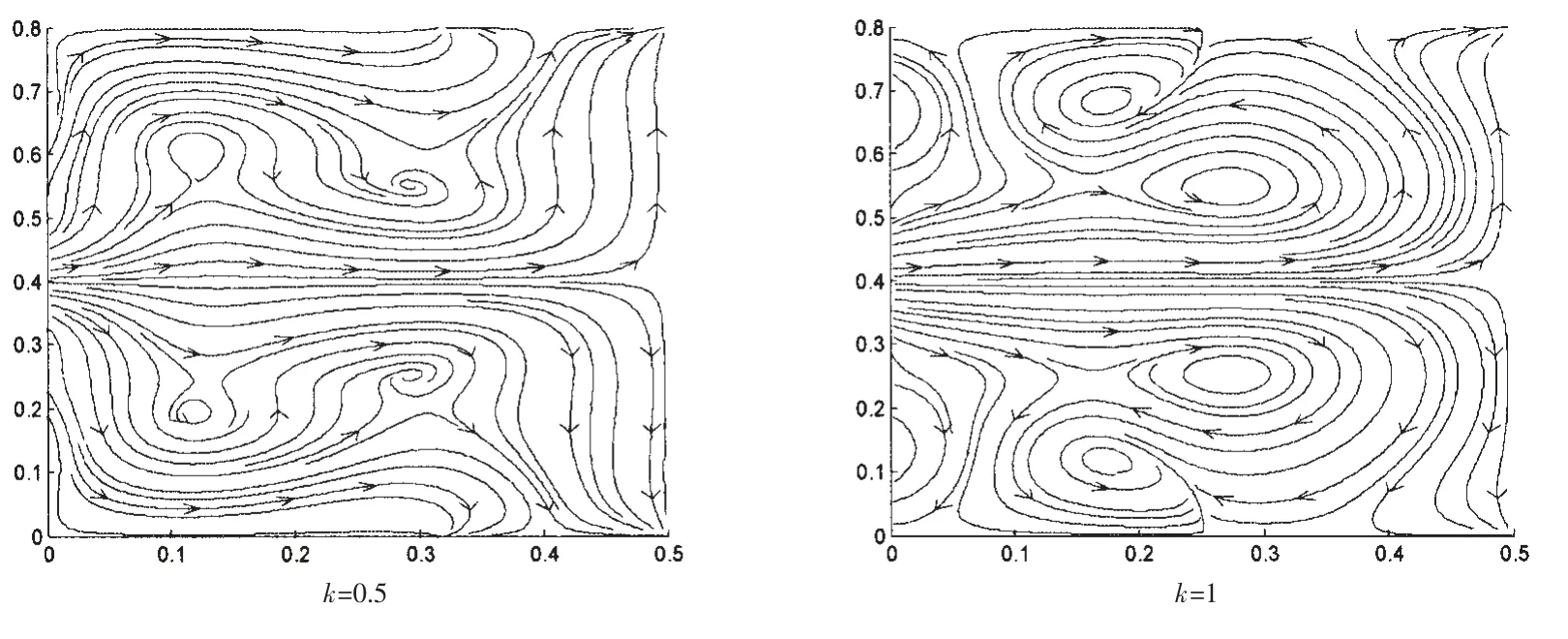

图9 不同梯度指数功能梯度板功率流流线图(912 Hz)Fig.9 The power flow streamline of an FGM plate with different graded indexes (912 Hz)
4 结 论
本文从功能梯度矩形板振动方程出发,利用动刚度法求解了结构固有频率及振动响应,结合功率流定义,得到了两边简支,另外两边简支、固支、自由三种边界条件功能梯度板振动输入功率流曲线、功率流矢量图与流线图,对不同边界条件与不同梯度指数的影响进行了分析研究。 结果表明,边界条件与梯度指数的变化,会影响板的刚度变化,刚度越大,FGM 板的固有频率越大,板内功率流漩涡结构减少,能量沿单方向传递。 通过本文研究得到了功能梯度板内功率流传播特性,为功能梯度材料在结构振动噪声控制、激励源识别及传播路径分析提供了理论依据。

