不同板式透空堤消浪性能的数值研究

李雪艳， 王 庆， 朱小松， 郭为军，

张俊斌1， 王丽雪1， 张之晨1， 李 钦1

（1. 鲁东大学 海岸研究所， 山东 烟台264025； 2. 中海油研究总院有限责任公司， 北京100000；3. 大连海事大学 环境科学与工程学院， 辽宁 大连116026）

0 引 言

随着我国海洋经济快速发展和“海上丝绸之路”经济带的建设，许多大型港口、码头、海洋平台、跨海大桥、浮式飞机场和人工岛等正逐步向海况恶劣、地质条件复杂的较深海域发展[1]。 在此背景下，传统的防波堤已无法满足海洋工程建设的要求。 板式防波堤作为一种新型透空式防波堤， 因其结构简单、施工方便、生态环保和利于水体自由交换等优点[2]，能够更好地满足海洋工程建设的要求，有关其结构形式、消浪性能等方面的研究日益得到国内外学者的重视[3]。

板式防波堤的消浪性能研究可追溯至上世纪中叶。1957 年，Stoker[4]率先在理论层面分析了长波作用条件下水下固定浮板的透射系数和反射系数。 随后，其他学者分别从理论分析[5-6]、模型试验[7-9]和数值模拟[10-11]等方面开展了系统深入的研究工作。 邱大洪[5]基于波能流理论推导了单一平板在任意水深条件下的解析表达式。 Wang 等[7]通过物理模型试验分析了多层平板式防波堤的消浪性能。 程永舟等[12-13]提出了一种新型透空格栅板式防波堤，并根据物理模型试验结果讨论了其消浪特性。王科等[10-11]应用边界元方法，研究了竖直单板和平板的消浪性能及消波机理。 Li 等[14]基于VOF 方法，数值分析了双层水平板型防波堤的消浪特性与机理。

以上围绕防波堤消浪性能开展的研究均针对水平板、垂直板式，有关弧板透空式防波堤则较少涉及。受半圆型防波堤启发，潘春昌和王国玉等[15-16]提出了一种新型弧板透空式防波堤结构，并针对该新型弧板式防波堤开展了试验研究，结果表明圆弧板透空式防波堤的消波效果优于水平板式透空堤。 王科等[17]基于波浪绕射和辐射理论，采用边界元方法对弧板式防波堤的消浪效果进行了研究，指出在潜深与波高的比值为0.05 时，与平板式防波堤相比上弧板式防波堤的消浪效果要提升约50%。 该研究仅考虑了单层弧形板透空堤在静水面下方的消浪情况，而没有考虑其不同出水状态时的消浪效果。

从现有文献报道可知，作为一种新型防波堤结构型式的弧板式透空堤，具有较为显著的消浪效果[15-17]。 已有研究均采用物理模型试验和边界元方法相结合的技术路线，其中物理模型试验存在对试验场地要求高、试验周期长、试验成本高等客观实际，边界元方法则基于势流理论分析尚未考虑流体粘性的影响。考虑到现有研究存在的上述问题，本文将基于N-S 方程建立求解波浪与弧板式防波堤相互作用的数值模型，充分考虑流体粘性的影响，在比较不同板式透空堤消浪性能的基础上，提出一种消浪效果优良的弧板式结构。

1 数值模型

1.1 数值模型构建

本文在Fluent 软件基础上，通过采用UDF（User Defined Function）编程实现速度造波与阻尼消波来构建数值模型。 所采用控制方程包括连续方程和动量方程，详见方程（1）-（3）。

连续方程:

动量方程:

式中:u 和v 分别为流体在x 和y 方向的速度分量；p 为流体压强；ρ 为流体密度；ν 为流体黏性系数；gx为水平方向重力加速度，取值为零；gy为垂直方向的重力加速度，取值为9.81 N/kg；μ（）x 为消波系数，对于流体区域取值为零，对于阻尼消波段为在阻尼段起点为零的单调递增函数。

采用VOF 方法[18]根据各个时刻流体在网格单元中所占体积函数F 的不同来构造和追踪自由表面，流体体积函数F 为网格单元中流体体积所占网格单元总体积的份额。 若某时刻网格单元全部充满流体，则F=1，为流体单元；若某时刻网格单元全部充满空气，则F=0，为空单元；若某时刻网格单元中同时有流体和空气，则0＜F＜1，为部分流体单元。 根据相邻网格的流体体积函数F 和网格单元边界上的流体速度来确定计算网格单元的流体体积， 综合考虑相邻网格单元的流体体积函数F 来确定自由表面的位置和形状。

控制方程采用中心差分格式进行离散。 压力速度耦合方式采用PISO（Pressure Implicit with Splitting of Operators）算法，包含一个预测步和两个修正步。 设定数值水槽左侧为造波边界，采用速度造波方法产生稳定的二阶Stokes 波。 设定数值水槽右侧为阻尼消波段，长度设定为2 倍波长，消波系数在消波起始位置设为零，在消波段末尾设为1，在消波中间段采用幂指数形式计算。数值水槽底部边界采用光滑壁面条件，法向速度为0。

1.2 数值模型验证

利用上述方法建立长60 m、高2 m 的空水槽模型（图1）。 利用该数值模型对水深d=1 m、波高H=10 cm 和周期T=1.8 s 的规则波进行模拟，并将距离造波位置x=10 m、20 m、30 m 和40 m 处的数值结果与理论结果进行了对比（图2）。结果表明，本文所建立的数值模型计算结果与理论结果吻合良好，能够在水槽内产生持续稳定的规则波浪。

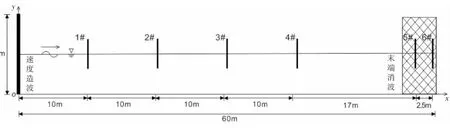
图1 空水槽模型示意图Fig.1 The sketch of empty flume

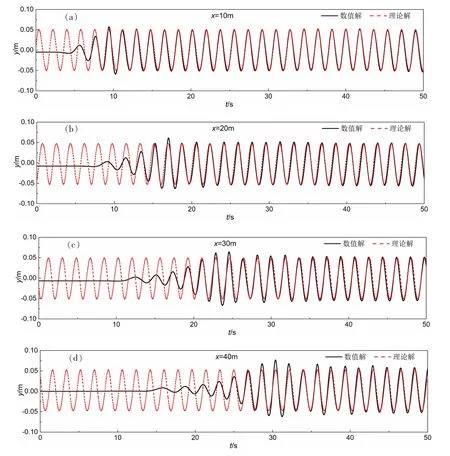
图2 流体区域波面历时曲线的计算值与理论值比较Fig.2 Comparison between numerical and theoretical results of wave surface located in the fluid region

图3 消波区域波面历时曲线的计算值与理论值比较Fig.3 Comparison between numerical and theoretical results of wave surface located in the wave attenuation region

数值水槽右端设有两倍波长的消波段， 对于水深d=1 m 和周期T=1.2 s 的波浪， 波长约为L=2.2 m。为了验证消波效果的有效性，分别在消波区域x=57 m（消波中间段）和x=59.5 m（消波末端段）位置处设置两个波面监测点，并将数值计算结果与理论结果进行了对比（如图3）。结果表明，当波浪传到消波中间区域（即x=57 m）时，波能已经衰减大部分； 当波浪传到接近水槽右端 （即x=59.5 m）时，波能几乎全部被吸收。 可见，本文所建立的数值模型具有良好的消波效果。

为进一步验证本数值模型的准确性，在上述空水槽中后部放置一平板式防波堤模型进行相关消浪性能的数值模拟。 参数设定和计算工况与Hsu 等[16]设置相同。 平板式防波堤模型长2 m，高0.04 m，入水深度为0.2 m，前端距离造波位置为30 m，浪高仪放置于板后方1 m 处。 将计算结果与前人透射系数的物模与数值结果[19-22]进行对比（如图4）。结果表明，本文计算结果与前人结果吻合较好。 鉴于前人数值模拟基于势流理论，假定流体为理想流体，因此本文计算结果与其有一定的差异是可预期的。

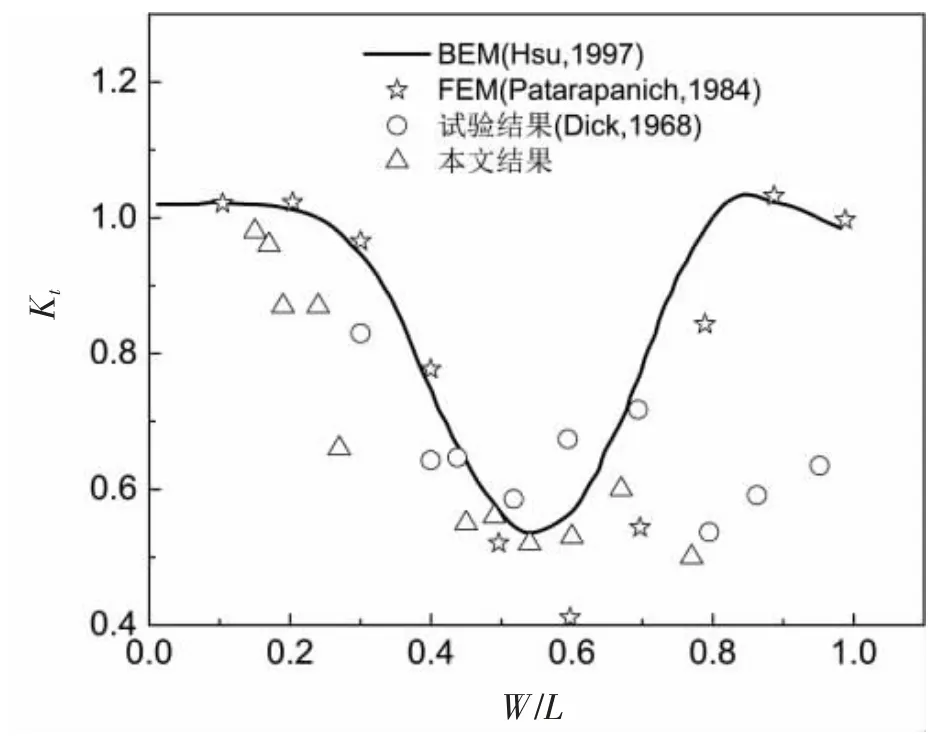
图4 本文透射系数与前人结果比较Fig.4 Comparison between the wave transmission results of this study and the predecessors

2 数值试验设计

本文共设计平板式（图5（a））、下弧板式（图5（b））和上弧板式（图5（c））三种透空堤结构。 三种透空堤板厚均为0.02 m，板长W 为1 m。 采用弧板高度刻画圆弧半径，高度d0取值为0.1 m。 d 为潜深，对于平板式透空堤，以板上表面边界为参考线，在水面以下为正，水面以上为负；对于下弧板式透空堤，以弧板上表面最高点处切线为参考线，正负定义同平板式堤；对于上弧板式防波堤，以板上部最高点连线为参考线，正负定义同平板式堤。

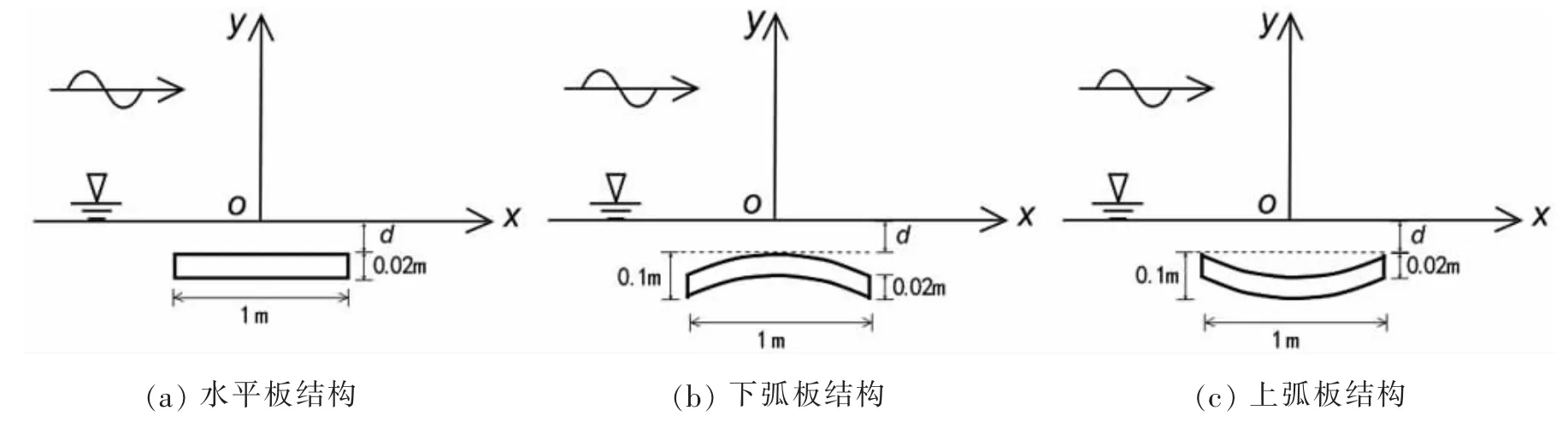
图5 平板与弧板透空堤示意图Fig.5 Sketches of horizontal and arc plate open breakwaters

本文计算水深h=1 m，规则波的波高H 分别为0.10 m、0.12 m 和0.14 m，周期T 分别为1.2 s、1.4 s、1.6 s、1.8 s 和2.0 s。潜深d 分别为-0.04 m（参考线位于静水面上方0.04 m）、-0.02 m（参考线位于静水面上方0.02 m）、0 m（参考线与静水面重合）、0.02 m（参考线位于静水面下方0.02 m）和0.04 m（参考线位于静水面下方0.04 m）。

基于上述已验证的数值模型，本文将分别对平板式、上弧板式和下弧板式透空堤的消浪特性进行系统的数值模拟。下弧板式防波堤结构放置于数值水槽中后部，其前端距造波位置30 m。数值水槽左侧为速度造波区，可产生长时间平稳的规则波（图2）。数值水槽右端设置有2 倍波长的消浪区。模型迎浪向一侧布置有两根浪高仪，间距为四分之一波长，目的是利用Goda 两点法[23]计算波浪的反射系数。模型背浪向一侧布置有三根浪高仪，目的是分析波浪的透射系数。

3 数值结果分析与讨论

根据上一章中数值参数的设定，本文将针对平板式、下弧板式和上弧板式透空堤，共设计225 种工况开展其消浪性能数值模拟。

3.1 计算网格剖分

本文设计平板式、下弧板式和上弧板式三种透空堤结构，根据不同结构模型的特点，分别进行计算区域的网格剖分。 为兼顾数值精度和计算效率，在静水面和结构模型附近进行网格加密。 整个计算区域以板式堤模型为中心共分10 块，采用结构化网格剖分。对于平板式透空堤，块2、块5、块6 和块9加密区网格尺寸为长x=6 cm、宽y=2 cm，其余非加密区网格尺寸为长x=6 cm、宽y=4 cm；对于弧板式堤，块2 和块9 加密区网格尺寸为长x=6 cm、宽y=2 cm，块5 和块6 区域网格尺寸为长x=4 cm、宽y=2 cm，块4 和块7 网格尺寸为长x=4 cm、宽y=4 cm， 其它区域网格尺寸为长x=6 cm、宽y=4 cm（图6）。

图6 透空堤局部网格示意图Fig.6 Part of the grid sketch of open breakwaters

3.2 不同板式透空堤结构消浪性能比较

3.2.1 波面历时曲线

水深h=1 m、周期T=1.2 s、波高H=0.1 m 和潜深d=-0.02 m（透空堤上表面高出静水面0.02 m）情况下，平板式、下弧板式和上弧板式透空堤的典型波面历时曲线比较详见图7 所示。 结果表明，在潜深d=-0.02 m 情况下， 下弧板式透空堤模型背浪侧3#、4#和5#测点的波面高程明显低于其它两种结构型式。由此可知，下弧板式透空堤的消浪性能要优于平板式和上弧板式透空堤的消浪性能。此外，下弧板式透空堤模型迎浪侧1#和2#测点的波面高程同样低于其它两种结构型式的波面高程。 这表明，下弧板式透空堤的反射波能要低于平板式和上弧板式透空堤的反射波能。

3.2.2 透射系数与反射系数

通过采集到的板式透空堤迎浪侧1# 和2# 测点的波面历时数据，由Goda 两点法[23]，将板式透空堤前的入射波高Hi和反射波高Hr分离。 通过采集到的板式透空堤背浪侧3#、4#和5#测点的波面历时数据，通过上跨零点法，统计得到模型后面的透射波高Ht。

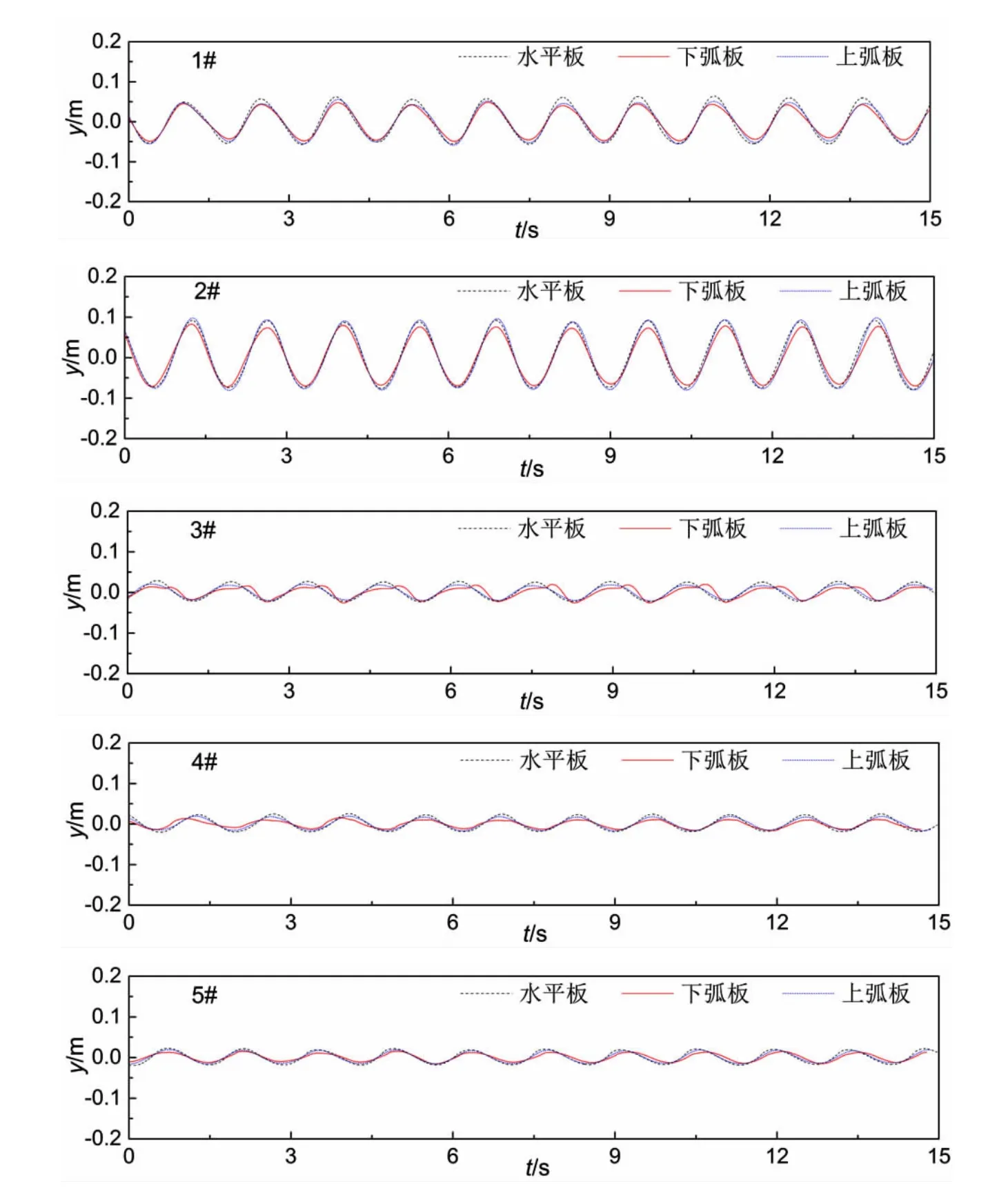
图7 不同监测位置处的波面历时曲线（h=1 m，T=1.2 s，H=0.1 m，d=-0.02 m）Fig.7 Time histories of wave elevations of measuring points (h=1 m, T=1.2 s, H=0.1 m, d=-0.02 m)

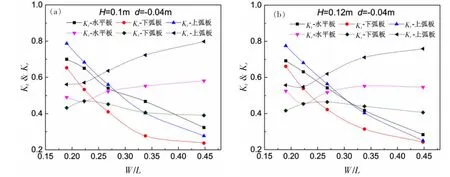
图8 给出了波高H=0.1 m 和0.12 m 情况下，在出水0.04 m、0.02 m 和0 m 情境时，板式透空堤对波浪的透射系数Kt和反射系数Kr随相对板宽的变化图。结果表明，在不同出水状态下，三种结构对波浪的透射系数均随着相对板宽的增大而减小； 平板式和上弧板式透空堤对波浪的反射系数随着相对板宽的增大而有所增大，下弧板式透空堤对波浪的反射系数随着相对板宽的增大变化不明显。 下弧板式透空堤的消浪性能较平板式和上弧板式优越， 在98%工况下其对波浪的透射系数和反射系数均低于平板式和上弧板式透空堤的结果。 相对板宽在0.19 至0.45 范围内，下弧板式透空堤相对于平板式和上弧板式对波浪的透射系数最高可分别减小约40%和31%， 对波浪的反射系数最高可分别减小约40%和43%。 由此可见，下弧板式透空堤不仅能显著降低波浪透过率，且同时能有效减少反射波能。

3.2.3 能耗系数

综合分析不同结构对波浪的透射系数Kt和反射系数Kr的结果可知，三种结构的消浪性能差别明显，其中以下弧板式透空堤的消浪性能最为显著。 这主要是因为不同结构在消浪原理上存在一定的差异。 平板式透空堤主要是通过破坏水质点的竖向运动轨迹，使波浪发生浅水效应进而破碎消能，减小透射波高。 下弧板式透空堤的迎浪面积较平板式透空堤大，且波浪需沿着堤面上爬，其对波浪的阻碍效果更加明显；此外，下弧板式透空堤能同时破坏水质点横向和竖向运动轨迹，浅水效应更加显著进而破碎现象更加剧烈，波能衰减更为显著，致使透射波高和反射波高均显著减小。 上弧板式透空堤由于迎浪面向下倾斜，与下弧板式透空堤相比较，水体没有上爬过程的消能作用，透射系数与反射较下弧板式透空堤均增大。

与平板式和上弧板式透空堤相比较，下弧板式透空堤不仅能显著降低对波浪的透射系数，同时能有效地减小对波浪的反射系数，是一种消浪效果优良的新型消浪结构。 三种透空堤结构均通过破坏自由水面附近水质点的运动轨迹消能，水体紊动消能是重要组成部分之一。 波能耗散系数定义为

图9 给出了不同波高、不同潜深情境下，平板式、下弧板式和上弧板式透空堤结构的能耗系数。 结果表明，与平板式和上弧板式透空堤结构相比较，下弧板式透空堤结构能够消耗更多的波浪能量，其消浪性能明显优于平板式和上弧板式透空堤。 相对板宽在0.19 至0.45 范围内，下弧板式透空堤对波浪的能耗系数相对于平板式堤提高范围在11.7%至36.7%之间。

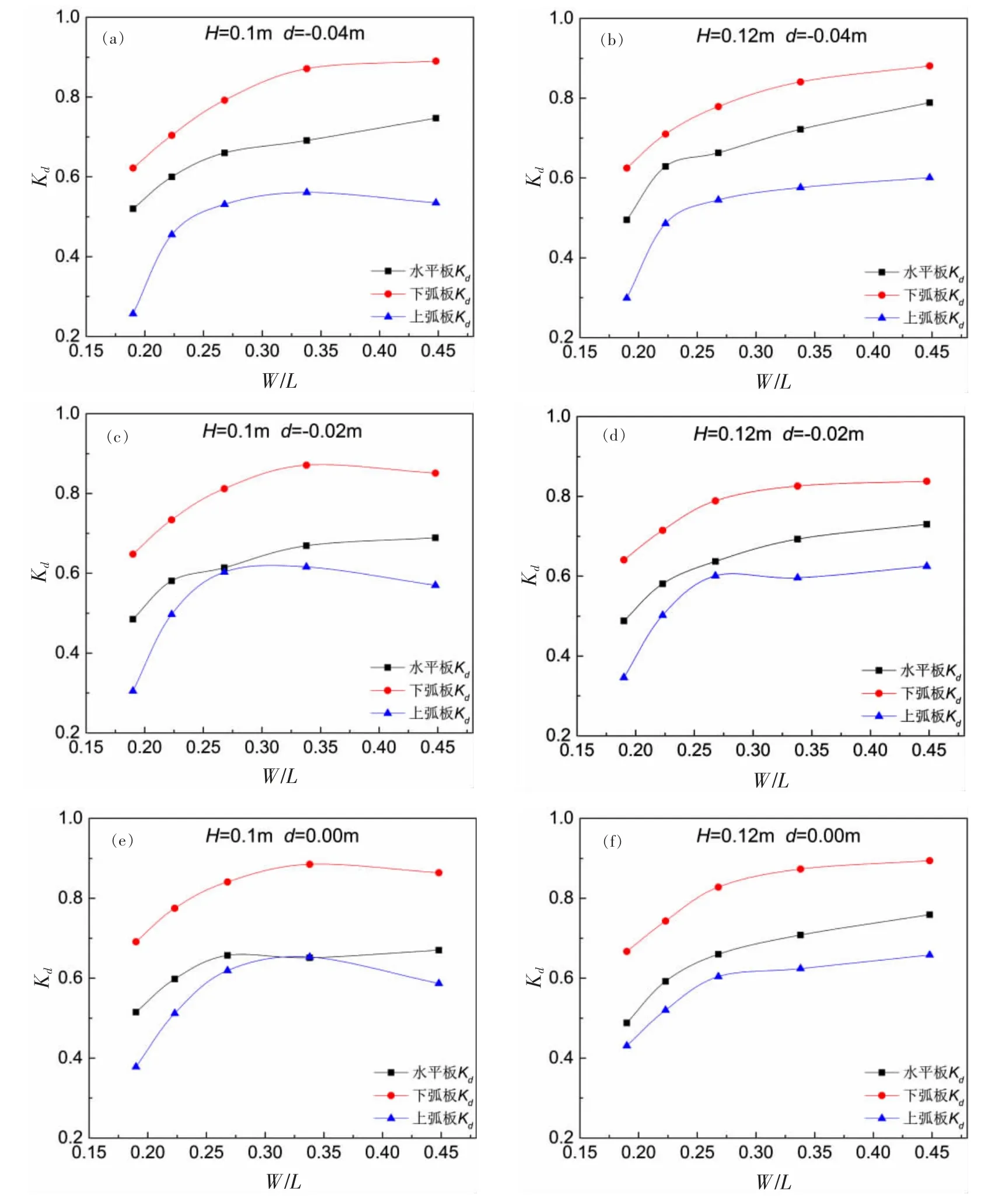
图9 不同板式透空堤对波浪的能耗系数随相对板宽的变化Fig.9 Variation of Kd with the relative width for the different open breakwaters

3.2.4 波能转化

图10 给出了相同潜深和波高、不同周期情况下，波浪与不同板式透空堤相互作用时的波能转化关系。 入射波与不同板式透空堤相互作用后其波浪能量主要转化为透射波能、反射波能和耗散波能。从图10（a）至图10（i）可以看出，对于不同板式透空堤，随着波浪周期的增大，透射波能占比明显增大，耗散波能和反射波能占比均减小。 在相同波浪要素情况下，下弧板式透空堤的耗散波能占比最大，在49.63%至55.37%之间，透射波能占比最小，在13.01%至23.41%之间。 下弧板式透空堤耗散波能占比较平板式透空堤增大31.15%至42.31%，较上弧板式透空堤增大42.04%至53.68%；其透射波能占比较平板式透空堤减小21.34%至23.52%，较上弧板式透空堤减小6.47%至20.29%。 由此可见，相同情境下，下弧板式透空堤可消耗更多的波浪能量，透射波能更少，消浪效果更加显著。

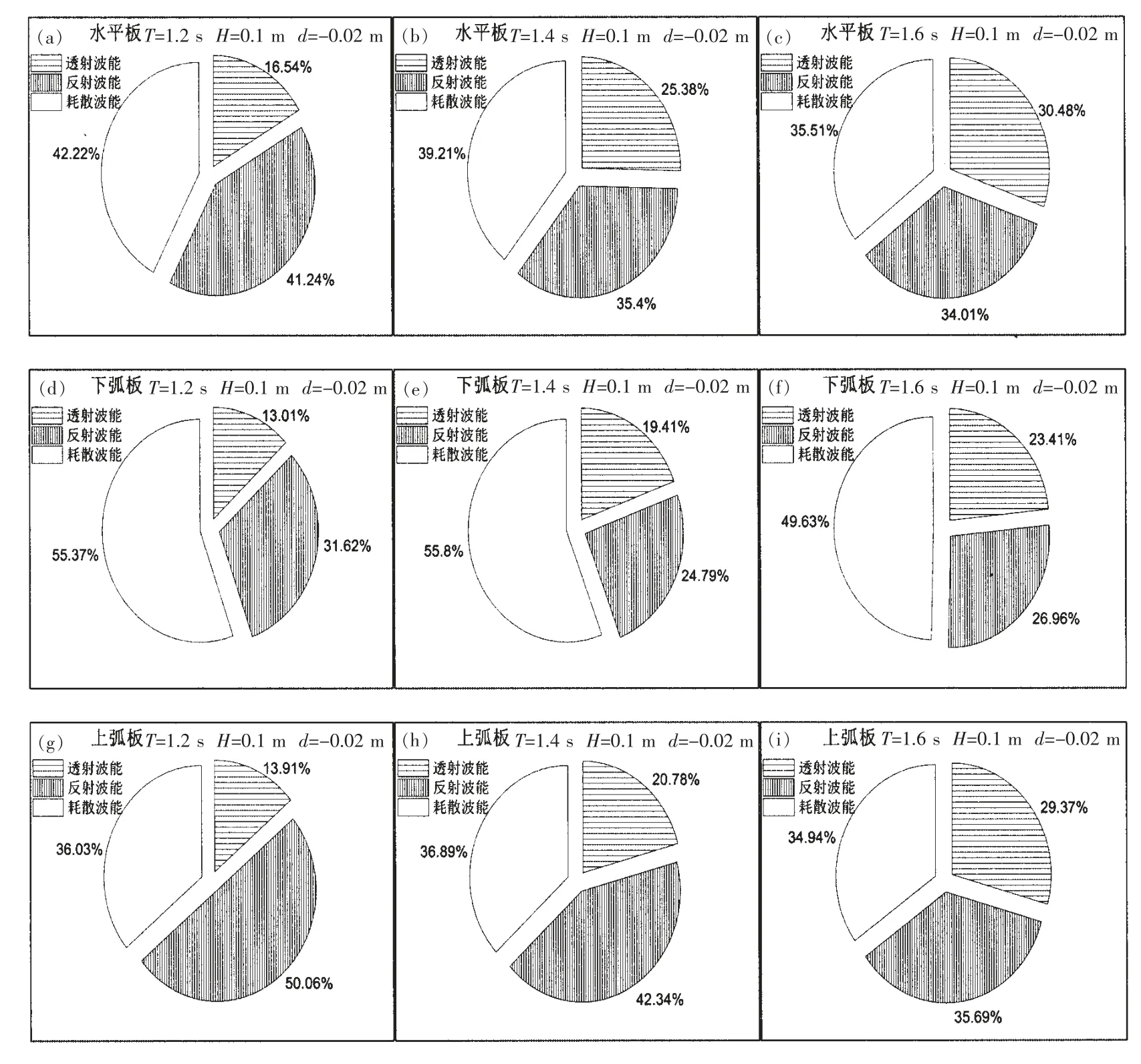
图10 不同板式透空堤波能转化关系图Fig.10 Relations of wave energy conversion of the different plate open breakwaters

4 结 论

本文基于N-S 方程构建了波浪与板式透空堤相互作用的数值模型，考虑了流体粘性的影响，共设计225 种工况开展消浪性能数值模拟，讨论了平板式、上弧板式和下弧板式3 种不同板式透空堤的消浪性能。 在潜深d=-0.04 m、-0.02 m 和0 m 情境下，主要得到以下结论:

（1） 下弧板式透空堤在结构迎浪面和背浪面不同监测位置处的波面高程均低于平板式和上弧板式透空堤。 波浪作用下其透射波能和反射波能均较小。

（2） 98%工况情境下，下弧板式透空堤对波浪的透射系数和反射系数均低于平板式和上弧板式透空堤，相对板宽在0.19 至0.45 范围内，下弧板式透空堤相对于平板式和上弧板式对波浪的透射系数最高可分别减小约40%和31%，对波浪的反射系数最高可分别减小约40%和43%。

（3） 下弧板式透空堤的消浪性能优越，在与波浪的相互作用中可以消耗更多的波浪能量，能耗系数最高，相对板宽在0.19 至0.45 范围内，下弧板式透空堤对波浪的能耗系数相对于平板式堤提高范围在11.7%至36.7%之间。

（4） 下弧板式透空堤的耗散波能占比最大，较平板式透空堤增大31.15%～42.31%，较上弧板式透空堤增大42.04%～53.68%。

（5） 综合考虑波面高程、透射系数、反射系数、能耗系数及耗散波能等指标，下弧板式透空堤的消浪性能最优。

致谢：本论文的研究工作曾得到大连理工大学王永学教授的热心帮助，同时也受益于与鲁东大学尤再进教授的多次讨论，在此向上述教授等表示诚挚的感谢！