应变率和应力三轴度对Q345B 钢动态力学性能的影响研究
孟利平, 程远征, 张伦平, 王海坤, 汪 俊, 刘建湖
(中国船舶科学研究中心, 江苏 无锡214082)
0 引 言
随着计算方法和计算程序的不断完善,通过数值仿真进行舰船结构抗爆抗冲击性能研究已越来越重要,而材料模型和相关参数的正确与否直接关系到仿真结果的正确性,进而影响结构抗爆抗冲击性能评估结论的正确性[1-3]。 Q345B 钢是工程结构中广泛使用的低合金钢,是船舶领域中军辅船、民船的主要结构材料,还是舰艇设备的结构用材料。所以针对Q345B 钢动态力学性能的研究对于军民用船结构的均衡设计、准确评估和防护优化等都具有很重要的意义。
国内对Q345B 钢动态力学性能的研究却不多。 部分研究者[4-5]进行了Q345 钢的动态试验研究,但都局限在高应变率(>103/s)对屈服强度的影响,缺乏中低应变率的试验数据,且对于各应变率下的大应变及断裂特性等缺乏较系统的试验研究。 对于船用钢材的模型及参数选取,国内大部分研究者均采用低碳钢的CS 模型参数,姚熊亮[6]在对船用917 钢的研究中指出,在进行水下爆炸等仿真研究时,针对不同材料应采用试验等方法得到合理的参数。 此外,由于钢材在拉伸破坏时会发生颈缩,这导致断裂判据在有限元计算中受网格的影响很大, 如何避免这一影响在实际计算中还缺乏一个定量化的指导。
本文针对Q345B 钢进行了应变率0.002/s~3 040/s 范围内的单向拉伸试验,并进行了压缩、扭转及不同缺口半径试件拉伸试验, 得到了Q345B 钢在不同应变率和不同初始应力三轴度下的变形至断裂的实验结果,据此分析并修正了CS 本构模型,拟合了JC 失效模型,结合数值仿真,给出了失效判据在有限元计算中针对不同尺寸网格的使用方法,为Q345B 钢结构的工程设计与应用提供了依据。
1 试验研究
1.1 不同应变率拉伸试验
采用MTS 准静态材料试验机、Instron 高速材料试验机以及Hopkinson 拉杆进行了应变率在0.002/s~3 040/s 范围内的拉伸试验,具体的应变率值及相应加载方式见表1,每组试验进行3~5 次重复试验保证了数据的有效性。 所有试验均采用相同标距的试件以消除由于试件尺寸不同可能带来的影响。 试件形状为板状,厚度为4 mm,试件尺寸示意图及实物图如图1 所示,试件两端夹持段的长度依试验机夹持要求略有不同。
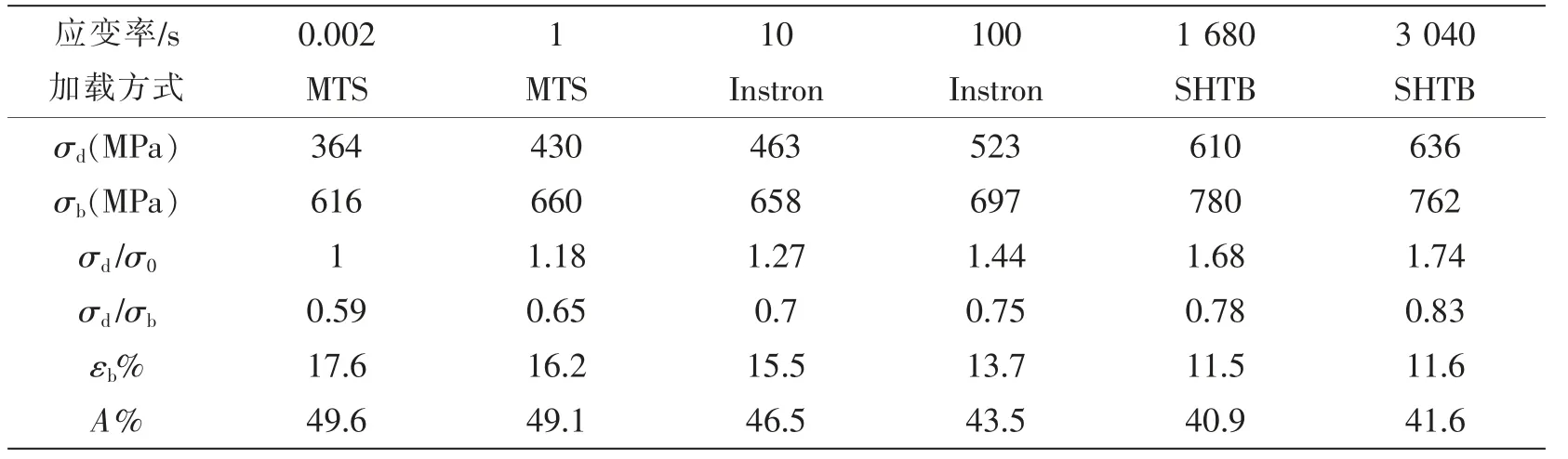
表1 Q345B 钢动态力学性能Tab.1 Dynamic mechanical property of Q345B steel

图1 试件形状尺寸示意图及实物图Fig.1 Shapes and sizes of test specimens
1.2 不同应力三轴度试验
采用电子万能试验机和电子扭转试验机进行了准静态压缩、扭转试验,以及不同缺口半径的拉伸试验。 压缩和扭转试验均采用圆柱型试件,压缩试验试件的高度与直径尺寸为15 mm×10 mm,高径比3:2;扭转试验试件标距段尺寸为10 mm×70 mm;带缺口试件的平行段直径φ=10 mm,缺口中心半径a=3 mm,缺口半径R 分别为2 mm,6 mm,8 mm 和18 mm,以及光滑圆棒(R→∞),各种试件如图2 所示,引伸计标距为50 mm。

图2 压缩、扭转及带缺口试件图Fig.2 Test specimens of pressure, torsion and the notched
2 不同应变率试验结果及对本构模型修正
2.1 不同应变率拉伸试验结果与分析
由Q345B 钢不同应变率拉伸试验, 得到0.002/s~3 040/s 之间共七个应变率下的工程应力应变曲线,如图3 所示。 可见Q345B 钢具有明显的应变率效应,随着应变率增大,屈服强度和抗拉强度均明显增大。 与准静态相比,应变率达到100/s 时,屈服强度增大将近50%,强化比(σd/σ0)达到1.42;应变率达到103/s 的量级时,动态屈服强度将近准静态时的两倍。当应变率大于103/s 时,应变率1 680/s 和3 040/s 两条曲线几乎重合在一起,说明在本文试验范围内,Q345B 钢存在一个应变率饱和值,达到该值后,应变率效应不再显著。
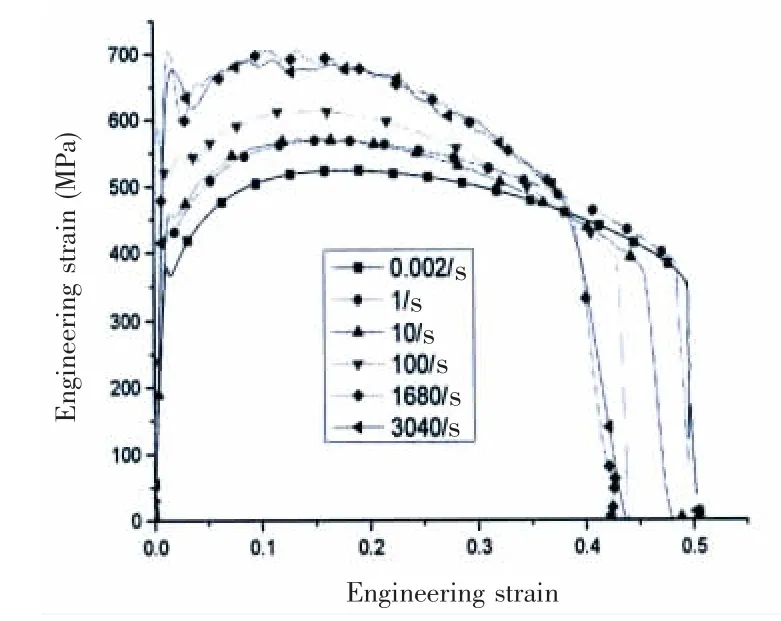
图3 各应变率下的工程应力应变曲线Fig.3 Engineering stress-strain at different rates

图4 σd/σ0 及σd/σb 与对数应变率的关系Fig.4 σd/σ0 and σd/σb as function of strain rate
表1 给出了Q345B 钢主要力学性能的试验结果。 其中,σd(MPa)为钢材各应变率下的屈服强度;σ0(MPa)为准静态(应变率0.002 s-1)时的屈服强度,此时有σd=σ0;σb(MPa)为抗拉强度;强化比为σd/σ0(准静态时为1);屈强比为σd/σb;A%为断裂延伸率;εb%为颈缩前的均匀延伸率,对应最大载荷时试件的伸长率。 将数据绘于图中,如图4 可清楚看出,Q345B 钢的强化比和屈强比随着应变率的对数呈近似线性关系增大。 屈强比增大, 直观上反映出应变率增大时Q345B 钢塑性变形的应变硬化能力减弱。图5 中,Q345B 钢的均匀伸长率随着应变率对数的增大而逐渐减小,表现为塑性失稳不断提前。材料的塑性变形和应力应变曲线的形状是应变硬化和动态回复竞争的结果[7],应变率提高后,塑性变形过程逐渐趋于绝热过程,变形功产生的热量来不及传出去,引起材料内部温度升高,温升软化与应变硬化相互竞争,导致高应变率变形时应变硬化作用的弱化;高应变率下材料塑性变形分布不均匀,往往会在局部区域滑移量累积过大,导致塑性失稳的提前。 图5 中断裂伸长率在高应变率区有所发散,但总体随应变率增大呈减小趋势,说明应变率提高会导致Q345B 钢延性降低。
Q345B 钢在不同应变率拉伸过程中均出现明显颈缩, 然后很快被拉断。 典型断口形状如图6,存在明显的剪切唇和纤维区,放射区不明显,根据宏观断口可以看出Q345B 钢具有良好的塑性,其断裂模式属于典型的韧性断裂[8]。 宏观断口形貌随应变率的变化没有明显差异,可初步判断应变率对Q345B钢的断裂方式没有重要影响。 对断裂机理的深入剖析,还需做进一步的微观研究。
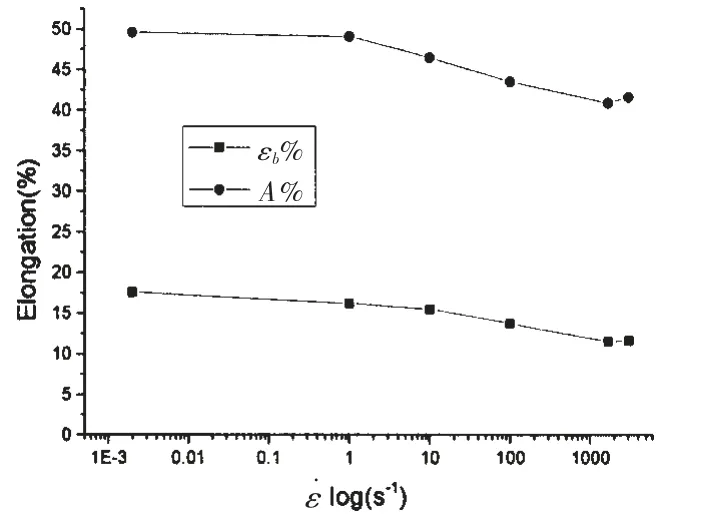
图5 均匀/断裂伸长率与对数应变率关系Fig.5 Uniform/fracture elongation as function of strain rate

图6 典型断口照片Fig.6 Typical fracture graph
2.2 动态本构模型分析与修正
2.2.1 应变率强化模型
在水下爆炸等数值仿真中,常用于金属动态变形的应变率强化模型有JC 模型[9]和CS 模型[10]。 JC模型用一个参数描述应变率对屈服强度的强化效应,其表达式为

式中:σd为动态屈服强度,MPa;σ0为准静态屈服强度,MPa;C 为材料参数;为无量纲应变率为塑性应变率,为参考塑性应变率。 取参考应变率为0.002/s,有σ0=364 MPa,根据各个应变率下的屈服强度和应变率对数的关系,利用最小二乘法拟合,得到C=0.046,拟合曲线如图7。
CS 模型不考虑参考应变率,采用两个参数描述应变率强化效应,其关系式为

式中D 和q 为材料参数。 由各应变率下的屈服强度和应变率的关系,利用最小二乘法拟合,得到D=13 709.45,q=5.55,拟合曲线如图8。

图7 JC 应变率强化模型拟合结果Fig.7 JC model fitting curve
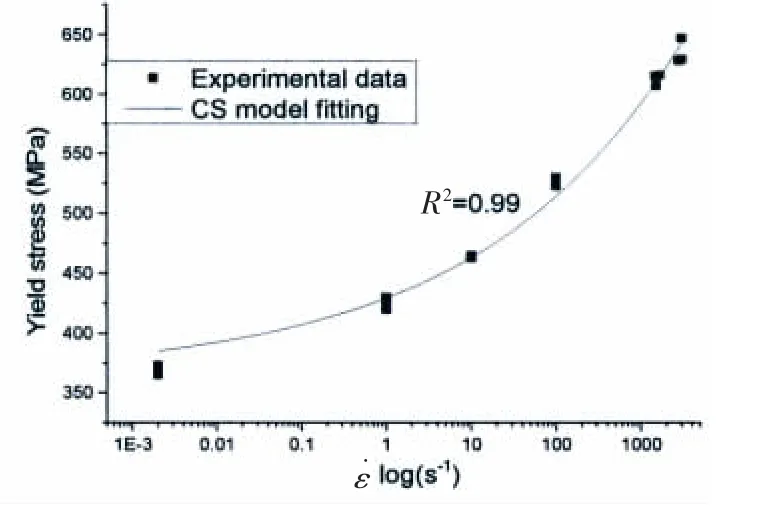
图8 CS 应变率强化模型拟合结果Fig.8 CS model fitting curve
比较图7 和图8,可以很清楚地看到,JC 模型采用屈服强度和应变对数的线性关系,拟合相关度较差,并不能很好地描述Q345B 钢的应变率强化效应;而CS 模型采用两个参数,能很好地预测Q345B钢的应变率强化效应。
2.2.2 模型修正
通过上节分析可知,为较好反映Q345B 钢的应变率强化效应,应采用CS 强化模型。 而CS 模型是理想刚塑性模型,其没有考虑应变硬化效应,对于材料动态屈服后塑性变形性能的预测能力不够。 在实际应用中,有研究者采用线性硬化模型与之配合使用[6],但这只是简化了的模型,不能真实反映材料的实际力学性能。 JC 模型采用幂律形式的函数描述材料的应变硬化效应,效果通常较好。
已知准静态塑性变形是等温过程,而对于高应变率变形,由于变形速度较快,材料内部因变形而产生的热量来不及传出去,导致了材料内部温度升高,材料高应变率变形过程中的温升为

式中:η 为塑性功-热转化因子,一般取η=0.9;ρ 为材料密度,cV为材料比热容。 由于温升将导致Q345B钢受到软化,则还需考虑温升软化效应。 结合JC 模型的乘积形式耦合应变率强化、应变硬化以及温度软化效应,给出以下修正模型:
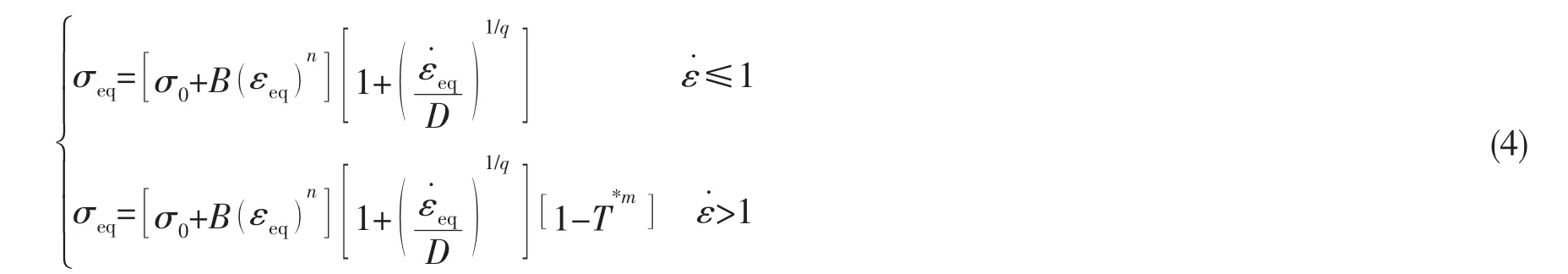
式中:T*=ΔT/Tm,Tm为钢的熔点温度;σeq,εeq,分别为等效塑性应力、 等效塑性应变和等效塑性应变率,为εeq的导数,σeq,εeq形式如下:

通过(5)式可将张量形式的应力应变等效为标量,以适用一维拉压等试验得出的本构方程。 (4)式中,σ0,D,q 取值与CS 模型一致,将σ0,D,q 值代入,通过准静态试验数据拟合参数B 和n,并选应变率10/s 的曲线拟合m。最终得到(4)式中:σ0=364 MPa,B=558 MPa,n=0.515,D=13 709.45,q=5.55,m=0.45。
需要说明,拉伸试验中试件达到抗拉强度时会发生颈缩失稳,颈缩之后变形不再均匀,而是处于三向应力状态,需进行Bridgman 修正[11]以得到等效真实应力,真实应变也需通过最小截面积得到。 而试验未能获得颈缩域的实时尺寸,本文在拟合上述参数时未考虑颈缩后的情况,只选取抗拉强度之前的数据进行拟合。注意到Q345B 钢在抗拉强度点已达到一定变形量,因此选取该段数据拟合的参数对于描述其真实变形情况已足够。 图9 为将参数代入修正模型后对各应变率曲线的预测结果,可以看到预测结果与试验曲线吻合较好。
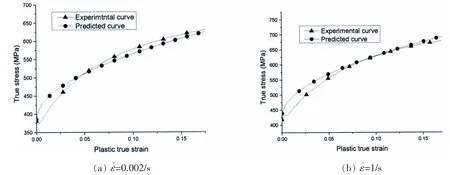

图9 修正模型预测效果的比较Fig.9 Modified model predicted results
2.3 应变率对断裂应变的影响
单向拉伸试验由于试件出现颈缩, 导致应变集中在较小范围,受试件尺寸的影响,由试验曲线得出的延伸率并不能反映材料的真实断裂应变,不能直接用于计算。基于塑性体积不可压缩理论,并假定断口截面应变均匀[12],可由(6)式计算试件的真实断裂应变:

式中A0和A 分别为试件的初始截面积和断口截面积。通过量取试件断口及原始试件截面积,得到Q345B 钢断裂应变与应变率对数的关系如图10,可见随着应变率增大,Q345B 钢的真实断裂应变整体呈减小趋势,由准静态时的1.27 降到应变率3 040/s 时的1.02。

图10 断裂应变与应变率关系Fig.10 Relationship of fracture strain and strain rate
3 不同应力三轴度试验结果及失效模型拟合
3.1 不同应力三轴度试验结果与分析
应力三轴度是表征材料内部受力状态的参量,表达式为η=σm/σeq,其中σm是静水压力,MPa,σeq是Mises 等效应力,MPa。根据Bridgman 的研究[11],带缺口试件中心处的初始应力三轴度可根据(7)式计算:

式中:R 是缺口半径;a 是缺口中心处圆棒半径。 则可得到各缺口半径试件中心处的初始应力三轴度,见表2,表2 中同时列出了压缩和扭转的应力三轴度,以及通过有限元计算得到的断裂时刻中心点处的应力三轴度和平均应力三轴度。 其中,初始值是原始试件最小截面中心处按(7)式计算的应力三轴度,断裂值是试件断裂时刻最小截面中心处有限元计算的应力三轴度,平均值是按(8)式计算的试件最小截面中心处在整个变形过程中的平均应力三轴度。 有限元计算过程见第3.2 节。
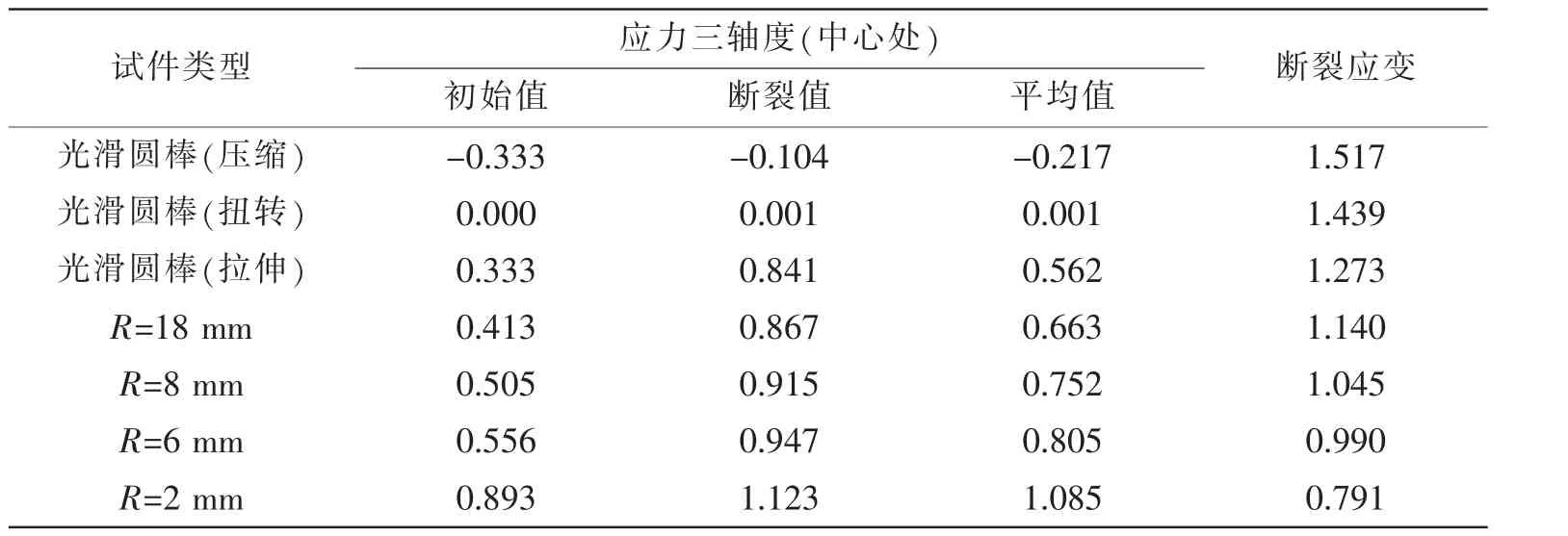
表2 Q345B 钢不同应力三轴度试验与计算结果Tab.2 Test and FEM results of Q345B steel at different stress triaxiality
图11 给出了各缺口试件拉伸的载荷位移曲线,从图中可以看出,随着缺口半径的减小(即应力三轴度增大),试件的断裂伸长率随之下降,同时最大载荷显著提高,表现出明显的缺口强化效应。 这是因为当应力三轴度提高时,受到其他两个方向的力的限制,体积应力和体积应变起的作用越来越大,使得材料的塑性变形比较困难,要达到相同的应变需要的应力就要提高;由于材料滑移变形受阻,只能产生较小的颈缩,应变进一步发展所受限制随缺口半径的减小而增大[13]。
压缩试验时,试件两端面受到摩擦力的作用,试件最终被压成圆鼓状,如图12 所示,压缩前后的试件尺寸如图12(a),试件未发生断裂。 扭转试件被均匀地扭转很多圈后断裂,如图13 所示,断口位于箭头所指处,与轴向垂直,较为平齐,属于典型的延性断裂。

图11 各缺口及圆棒试件的载荷位移曲线Fig.11 Load-displacement of notched /smooth specimens

图12 压缩试件变形前后对比Fig.12 Comparison of specimens before and after pressure

图13 扭转断裂试件Fig.13 Specimens after torsion fracture
3.2 应力三轴度和断裂应变的确定
对于缺口拉伸试验, 一般采用试件最小截面中心处的初始应力三轴度或者断裂时的应力三轴度作为整个过程的确定量, 这两种做法都忽略了试件变形过程中应力三轴度随应变的累计变化。 实际上,应力三轴度随着变形的进行是不断变化的,应该考虑应力三轴度在时间上随应变的累积效应,则定义平均应力三轴度,通过公式(8)确定各试件的应力三轴度值:

式中,εf是断裂应变。 应力三轴度η 是等效塑性应变的函数,由于试验中无法获取这个函数关系,本文借助有限元模拟来确定该关系。 根据对称条件,建立各缺口试件的二维轴对称模型,对缺口处进行网格细化,试件一端固定,另一端施加位移载荷,采用ABAQUS/Standard 对试件拉伸过程进行模拟,当计算输出的载荷位移曲线与试验的曲线一致后, 提取试件最小截面关键点的应力三轴度η εeq( )和等效塑性应变。
图14 给出了各缺口试件断裂时刻最小截面的应力三轴度和等效塑性应变沿径向的分布。 由于断裂时各试件的半径不一样,为了便于比较,将半径无量纲化,若r 是最小截面上某点的半径,a*是各试件断裂时最小截面的半径,则γ=r/a*。 由图14(a)可见各缺口试件断裂时,最小截面中心点的应力三轴度最大,沿径向逐渐减小,则选取中心点的应力三轴度进行分析;由图14(b)可见对于缺口半径R≥6 mm 的试件,最小截面断裂时的应变从中心沿径向逐渐减小,而R=2 mm 的试件相反,断裂应变从中心沿径向逐渐增大。观察拉伸过程看到,R=2 mm 的试件缺口根部出现了严重应力集中现象,这是导致其边缘断裂时应变比中心大的原因,但仍然是中心点发生断裂。 图15 给出各缺口试件最小截面中心处的应力三轴度随应变的变化,可见在拉伸过程中,试件的应力三轴度不断变化,总体呈增大趋势。 对于扭转和压缩试件,同样采用有限元模拟确定应力三轴度η εeq( )关系,根据(8)式即可计算得到各试件对应的平均应力三轴度。

图14 断裂时刻最小截面应力三轴度和等效塑性应变的径向分布Fig.14 Stress triaxiality and effective plastic strain along the minimum section ratio at fracture

图15 最小截面中心应力三轴度随应变的变化Fig.15 Stress triaxiality as strain varies at the section minimum center

图16 JC 失效模型的参数拟合及外插Fig.16 JC failure model parameters fitting and extrapolation
各缺口试件和扭转试件的断裂应变均采用有限元计算对应试验断裂时刻的最大等效塑性应变。压缩试件试验时没有失效,说明负应力三轴度时断裂应变较其他大,则本文直接通过外插由剪切和缺口试件拟合的曲线得到压缩及其他负应力三轴度对应的断裂应变值,如图16。表2 中给出了相应的试验及计算结果。
3.3 J-C 失效模型参数拟合
材料失效具有较复杂的机理,延性断裂一般有空穴成核聚集断裂、剪切断裂等模式,在动力学有限元计算中,主要的失效模型有最大塑性应变、最大主应力、最大主应变、Johnson-Cook 失效模型等,其中最常用的是Johnson-Cook 失效模型,表达式为

式中:D 为损伤变量,当D=1 时材料失效;εf为断裂应变,不考虑温度的表达式为

第一大项反映了应力三轴度对断裂应变的影响,第二大项反映应变率的影响,两项效应叠加。
根据平均应力三轴度与断裂应变的关系, 结合断裂应变与应变率的关系, 利用最小二乘法拟合(10)式。 拟合参数时未计入压缩时的断裂应变,得到:D1=1.734,D2=-0.281,D3=1.134,D4=-0.013,将参数代入并外插得到压缩及其他负应力三轴度对应的断裂应变,如图16。
4 失效判据的网格依赖性分析
在有限元仿真中,是通过单元的失效来模拟结构的破坏,当单元满足失效判据时,将单元删除。JC失效模型以断裂应变作为失效判据,通过材料试验得到的断裂应变是材料的真实力学性能,材料断裂时变形高度集中在较小的范围,要真实模拟材料的断裂行为,断裂处的单元需划分很细。 而在实际结构计算中,考虑计算成本等因素,通常失效单元的尺寸比材料断裂区域的尺寸要大很多,如简单使用材料断裂试验得到的失效判据,将会带来较大误差,这时就涉及到如何正确使用失效判据的问题。 针对此问题,运用ABAQUS/Standard 建立试件的有限元模型,选择不同尺寸的单元进行单向拉伸试验模拟,输出计算的载荷位移曲线与试验曲线比较,确定不同单元尺寸所对应的断裂应变。
选择光滑圆棒的准静态拉伸试验进行模拟,根据轴对称条件建立试件的二维轴对称模型,共对10种不同单元尺寸的模型进行模拟,具体单元尺寸见表3,有限元模型如图17。 固定试件为一端,在另一端施加位移载荷。 计算得到的断裂应变随单元尺寸的关系见表3, 图18 给出了单元0.05 mm 和0.1 mm 的计算结果与试验结果对比,可见两种尺寸基本完全重合,说明此时的单元尺寸已能模拟出试件真实的变形情况,则可认为0.05 mm 单元的断裂应变即为材料的真实断裂应变。

图17 不同单元尺寸的有限元模型Fig.17 FEM model of different size of grids

图18 两种尺寸单元的计算结果与试验对比Fig.18 Comparison of FEM results of two meshes with the test

表3 不同尺寸单元对应的断裂应变Tab.3 Fracture strain with different size of grids
图19 为断裂应变与单元尺寸的关系,可见开始时,随着单元尺寸增大,断裂应变逐渐减小;当单元尺寸大于1 mm 时,断裂应变迅速减小;当单元尺寸增大到约15 mm 以后,断裂应变逐渐趋于稳定。 记0.05 mm 单元的断裂应变为εf0, 令修正系数为α=εf0/εfc,εfc为其他尺寸单元的断裂应变, 则修正系数α 与单元尺寸s(mm)存在(11)式所示关系,拟合结果见图19。

图19 修正系数α 随单元尺寸的变化关系Fig.19 The parameter α as function of size of grids

综合以上分析,可知失效判据应是应变率、应力三轴度以及单元尺寸函数, 则进行考虑单元尺寸的JC 失效判据修正,得到

代入参数得到最终表达式为

5 结 论
针对Q345B 钢进行了准静态、中低应变率和高应变率以及不同应力三轴度的试验研究和数值计算,修正得到适用于Q345B 钢的本构模型和断裂判据,并形成如下具有工程应用价值的结论:
(1) 应变率对Q345B 钢的屈服强度和抗拉强度影响显著,当应变率增大到3 040/s 时,屈服强度增大为准静态的1.74 倍,抗拉强度为准静态的1.24 倍;
(2) Q345B 钢的断裂呈典型的韧性断裂特征,断裂伸长率随应变率增大总体呈下降趋势,当应变率增大到3 040/s 时,断裂伸长率由准静态的49.6%下降到41.8%;
(3) 应力三轴度对Q345B 钢的断裂应变影响显著,当应力三轴度由-0.217 增大到1.085 时,断裂应变由1.517 下降到0.791;
(4) 有限元计算中,材料的断裂应变受单元尺寸的影响,随着单元尺寸s(mm)的增大,单元断裂应变逐渐减小,对JC 失效模型进行考虑单元尺寸的修正后得到(13)式。

