基于ANSYS 的锥台形观察窗光学性能分析

陈 薇， 张爱锋

（中国船舶科学研究中心， 江苏 无锡214082）

0 引 言

观察窗是深海耐压结构的关键部件，其作用包括:（1） 作为耐压壳结构的一部分承载深海水压；（2） 作为可视窗口使得舱内的技术人员能够对深海环境进行直接观察，并同步进行舱外机械手的操控作业。 可用于制造观察窗的材料有有机玻璃、无机玻璃等，其中有机玻璃在破坏前会出现明显的挤压变形以提供破坏预警[1]，使舱内人员能够及时采取措施避免进一步破坏。 因此近年来，各国载人潜水器的观察窗材料仍以有机玻璃为主。 有机玻璃观察窗在使用工况下可能出现结构强度降低或破坏导致的机械失效，或者结构变形导致的图像失真，严重影响观察。

Stachiw 针对有机玻璃观察窗进行了大量短期载荷破坏试验和长期持续加载试验[2]，试验得到的数据和结论是《载人压力容器的安全标准》（ASME-PVHO）[3]的重要参考。 李向阳，崔维成[4]对深海载人潜水器的球形壳、舱口和观察窗进行了接触有限元分析，张端涛[5]采用接触有限元法对观察窗进行塑性变形分析。 廉俊盛[6]应用有限元软件模拟观察窗的蠕变，并与田常录等[7]的观察窗蠕变试验进行对比。杜娟[5]基于有限元分析将变形后的球扇形观察窗简化为“弯月形透镜”，并对其光学性能进行讨论。众多试验研究及有限元分析显示， 有机玻璃观察窗在深海水压直接加载时会产生观察窗与窗座的相对位移和观察窗上下表面的凹凸变形，其变形在保压状态下会因为蠕变进一步发展。 欧迎春[9]等提出透明材上下表面之间的厚度变化将导致透明件的局部光畸变， 并对航空透明件厚度变化引起的光学角偏差和光畸变进行了理论分析。 透明件光学畸变的试验测量方法包括投影法[10]、网格照相法[11]等。

本文以锥台形有机玻璃观察窗为研究对象，在ANSYS 有限元模拟的基础上，采用Matlab GUI 界面进行观察窗光学角偏差和光畸变的计算，建立了评价观察窗光学性能的理论方法，可用于观察窗光学性能的预测与评价。

1 锥台形观察窗结构特点

1.1 锥台形观察窗的设计参数

锥台形观察窗及窗座的基本结构如图1 所示，主要设计参数包括:厚度与低压面直径比t/D1，低压面直径与透光直径比D1/Df，观察窗锥形夹角α，观察窗低压面（小端）直径D1，观察窗与窗座接触面摩擦系数μ 等。

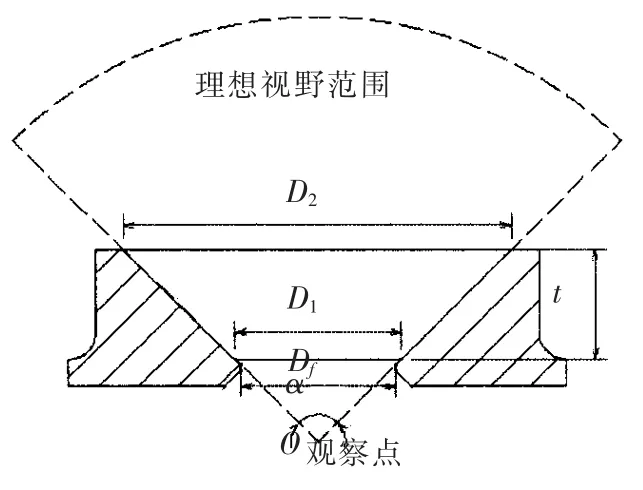
图1 锥台形观察窗基本结构Fig.1 The structure of conical viewport

1.2 锥台形观察窗变形的有限元模拟

按规范设计α=90°，t/D1=0.4，D1=100mm，上表面边缘45°倒角的观察窗模型作为算例， 在ANSYS 内建立1/2 二维轴对称模型（图2（a））。 装配观察窗时通常会在锥面涂抹润滑脂以减少摩擦力，因此可以认为接触面摩擦系数足够小，取μ=0.1。 有机玻璃杨氏模量为3 102 MPa，泊松比为0.35，拉伸强度为72.4 MPa，压缩屈服应力为124.1 MPa[12]。 窗座为钛合金结构，其杨氏模量远大于观察窗，因此将窗座设为目标面，将观察窗设为接触面，分别使用TARGE169 和CONTA172 单元建立接触对，采用ANSYS 的面-面接触分析，接触容差设置为0.01，其余参数默认。 在模型对称轴处施加对称位移约束，对窗座施加固定位移约束。 分别在观察窗上表面（即高压面）处施加0～70MPa 共8 组压力载荷。

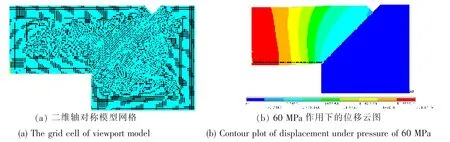
图2 观察窗的二维轴对称模型网格和位移云图Fig.2 The grid cell and contour of displacement of the viewport under pressure of 60 MPa

载荷作用下，观察窗上下表面各节点会出现不同程度的位移（图2（b）），可用各节点的位移来描述观察窗的结构变形。 建立以观察窗锥形顶点O 为原点的柱坐标系，根据每个节点的轴向与径向位移值，可将载荷作用下观察窗高压面和低压面上各节点变形后的坐标表示如图3。

从观察窗上下表面的曲线图可以看出，观察窗的变形程度与载荷有关。 加载状态下观察窗呈现高压面中部坑状凹陷，低压面整体凸出的变形特征，与文献[2]的试验结果基本一致；观察窗上下表面各点同时产生轴向和径向位移，表面之间的厚度发生改变，变形后的整体结构可视为非球面凹凸透镜。

图3 不同载荷作用下观察窗上下表面的变形曲线Fig.3 The deformation of low pressure surface and high pressure surface of viewport under different pressure levels

1.3 曲面的偶次非球面拟合

采用最小二乘法对有限元分析得到的锥台形观察窗高压面和低压面曲线进行多项式拟合， 由于结构和载荷均具有轴对称性，曲线拟合函数可选择偶次多项式，形式如下:

在本文算例中，考虑拟合度和函数复杂程度，选择6 次多项式进行拟合

应用Matlab 软件拟合计算可得到不同载荷作用下的观察窗表面曲线拟合函数（表1）。

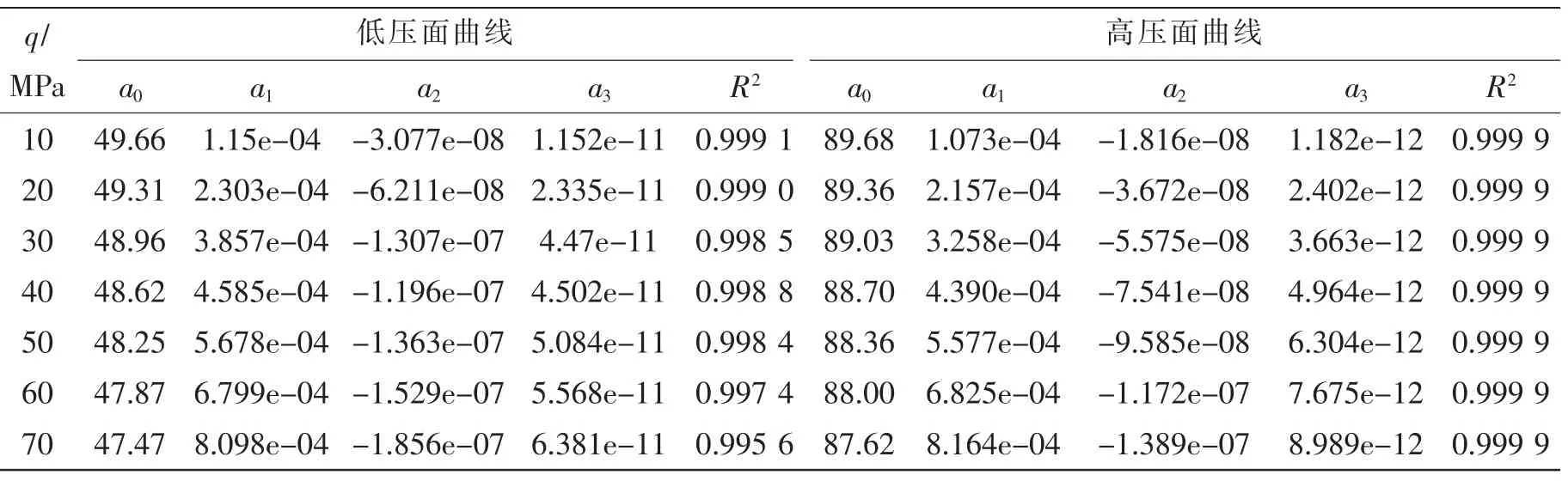
表1 锥台形有机玻璃观察窗低/高压面曲线拟合系数表Tab.1 The fitting coefficients of low/high pressure surface curve of conical acrylic viewport

2 锥台形观察窗光学性能

锥台形观察窗在耐压壳上的开口较小且耐压舱内空间有限， 人眼需靠近窗面以获取足够的视野范围，因此会造成图像失真[1]。 失真的原因之一是由光线在空气、有机玻璃和海水之间的折射导致的光学畸变。 在观察窗设计阶段，并无实物产品进行光畸变测量试验，可基于有限元模拟结果进行光学性能预测分析。

当人眼位于锥台形观察窗的锥形顶点处时， 任何一束透过观察窗进入人眼的光线均能找到与之对应的观察窗截平面使得入射光与出射光均在该平面上。 因此可将研究对象简化为平面光线折射模型。 由于光线可逆，现假设人眼处为光线发射点，光线与观察窗光轴的夹角记作视角β。

2.1 观察窗光学角偏差的理论计算

光学角偏差是由透明体几何尺寸和内部材料折射系数的非线性引起的光线传播方向的改变[9]，若光线经过多次折射，则最后一次折射光线与第一次入射光线的夹角记作光学角偏差θ（图4）。

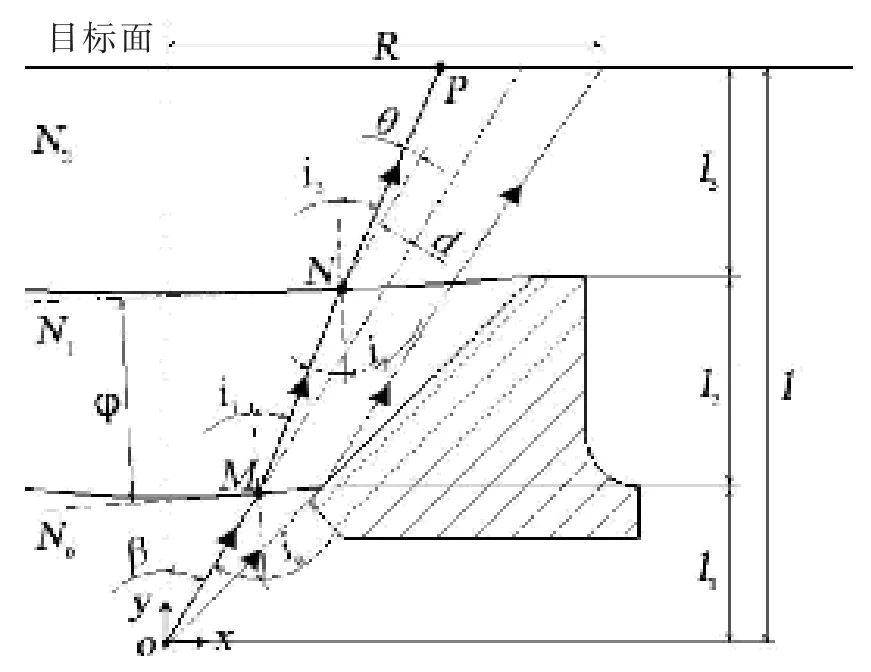
图4 锥台形观察窗的光学角偏差Fig.4 The optical angular deviation of conical viewport

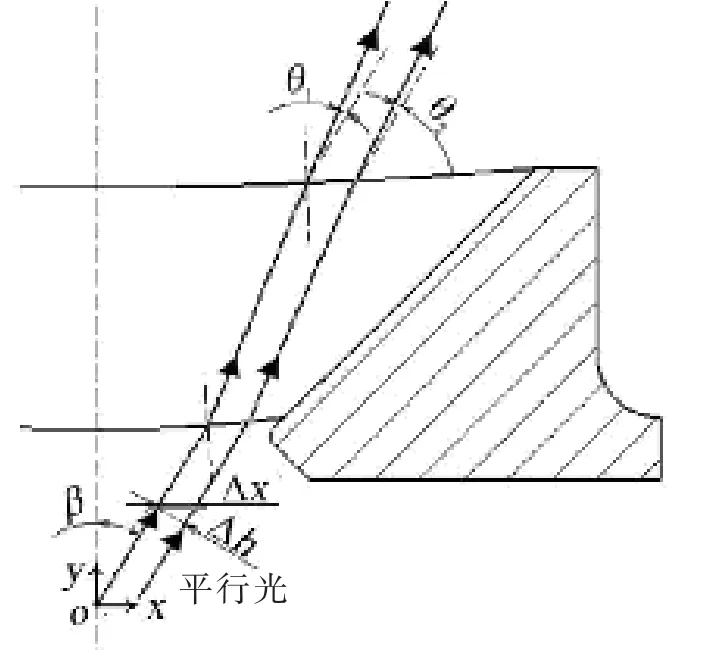
图5 观察窗光学畸变定义Fig.5 The definition of optical distortion

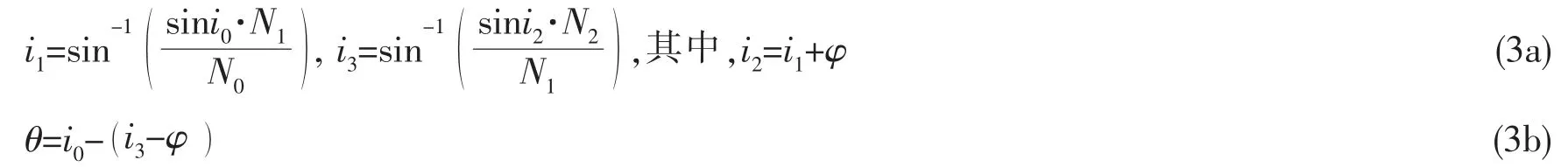
由几何光学原理可得光在透过曲面透明体时的光线方程:式中:i0为第一次折射的入射角；i1为第一次折射的出射角；i2为第二次折射的入射角；i3为第二次折射的出射角；φ 为第一次折射点的切线和第二次折射点的切线的夹角（逆时针变化为正）；N0为空气的折射率；N1为有机玻璃的折射率；N2为海水的折射率；θ 为光学角偏差。

视野范围为在观察点可观察到距离为l 的目标面的最大面积，其半径记作视野半径R，有

式中:βm为最大视角；l1为第一次折射点到观察点平面的垂直距离；l2为第一次折射点到第二次折射点的垂直距离；l3为第二次折射点到目标面的垂直距离。

2.2 观察窗的光学畸变

光学畸变是由透明件区域光学角偏差的变化产生[9]，可用间距为Δh 的平行光透过透明件时的光学角偏差的差值进行表征（图5），记作透明件的光畸变D[10]

式中:θ1为第一束平行光产生的光学角偏差；θ2为第二束平行光产生的光学角偏差；Δh 为两束平行光的间距。

2.3 Matlab 计算

2.3.1 光学角偏差与视野半径

以观察点O 为原点建立直角坐标系（图4），则光学角偏差可由公式（3）进行推导。 记低压面曲线函数y= f1（x ），高压面曲线函数y= f2（x ），已知透过观察窗进入眼睛的某一束细光线记作直线l0。

由于光线可逆，现假设从原点O 发射光线l0:y=k0x，其中k0为光线l0的斜率；联立低压面曲线函数y= f1（x ）可得交点M （xm, ym）。

第一次折射过程中入射角为

出射光的斜率k2有

第一次折射的出射光直线l2表示为

联立高压面曲线函数y= f2（x ）求得交点N （xn, yn）。

重复公式（6），同理可推导出第二次折射过程中的入射角i2，高压面曲线在N 点的切线斜率k3，出射角i3和出射光斜率k4。

光学角偏差为

第二次折射的出射光直线l4表示为

与直线y=l 联立求得第二次折射的出射光与距离原点l 的目标面交于点P （xp, yp）。

在目标面的视野半径R:

2.3.2 光学畸变

当平行光与光轴夹角为β 时，

Δh→0 时，光畸变为

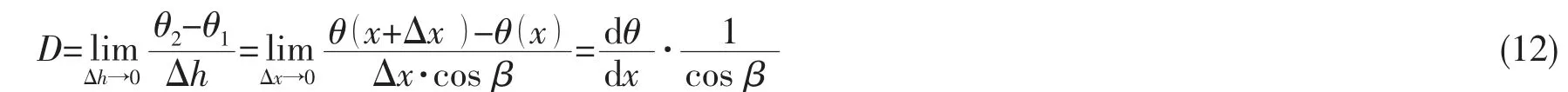
式中:θ1为第一束平行光产生的光学角偏差；θ2为第二束平行光产生的光学角偏差；Δh 为两束平行光的间距；β 为平行光与光轴的夹角；x 为入射光直线与变形前的观察窗低压面直线的交点的横坐标。

3 结构变形对光学性能的影响

3.1 结构变形对光学角偏差的影响

图6 计算观察窗光学角偏差的Matlab GUI 界面Fig.6 The GUI interface to calculate optical angular deviation of viewport

加载后观察窗产生变形，其变形程度与载荷有关，根据公式（6）～（9）编写Matlab GUI 程序，建立Matlab 图形用户界面， 基于ANSYS 模拟结果设置观察窗高压面和低压面表面曲线函数的参数，输入项为以指定视角进入人眼的光线，由光线的可逆性即可计算出该视角的光学角偏差，并作出光线折射图像（图6）。 整理数据即可绘制不同载荷作用下的光学角偏差-视角曲线图（图7）。

可以看出，观察窗变形程度一定时，光学角偏差随着视角的增大而增加；视角一定时，光学角偏差随着观察窗变形的增大而增加；视角越大的区域的光学角偏差值对观察窗结构的变形越敏感。

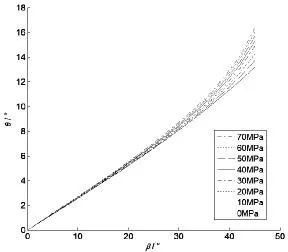
图7 光学角偏差与视角关系曲线Fig.7 Optical angular deviation versus visual angle

3.2 结构变形对视野半径的影响

观察窗最大视角βm取45°，目标面与观察点的距离l 取1 000 mm，输入Matlab GUI 界面计算xp，输出结果整理如表2。可以看出，随着载荷的增加，观察窗变形增大，透过观察窗能看到的视野范围随之缩小。 载荷为70 MPa 时，视野面积较加载前缩小约20%。

表2 锥台形有机玻璃观察窗视野半径表（l=1 000 mm）Tab.2 Radius of vision field of conical acrylic viewport

3.3 结构变形对光学畸变的影响

加载前观察窗的高压面与低压面平行，即φ=0，i1=i2，i0=β，图5 所示的平行光射入观察窗时，每一束光线的入射角相等且与x 无关，代入（13）式和（12）式得此时的光学畸变D=0。

加载后观察窗产生变形，其变形程度与载荷有关，根据Matlab 的计算结果绘制光学角偏差曲线后对其进行拟合计算并求导，得到不同角度的平行光透过观察窗各部位的光畸变值（图8～9）。

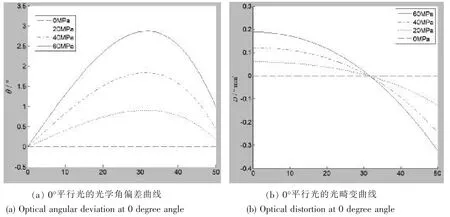
图8 0°平行光入射时的观察窗光学角偏差和光畸变Fig.8 Optical angular deviation and optical distortion of viewport at 0 degree angle

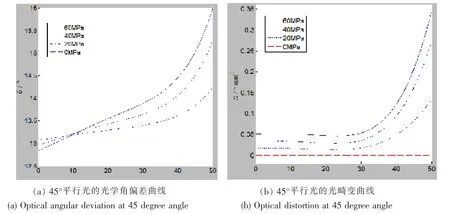
图9 45°平行光入射时的观察窗光学角偏差和光畸变Fig.9 Optical angular deviation and optical distortion of viewport at 45 degree angle

从曲线图可以看出， 当观察窗设计参数一定时， 加载前该观察窗的光学角偏差θ 仅与视角β 有关，因此对于任意视角β，观察窗无光学畸变；加载后，观察窗各部位的光学畸变值与变形程度及光线角度相关；光线角度一定时，光畸变值随着观察窗变形的增大而增加。

4 结 语

本文采用ANSYS 接触非线性分析方法计算了观察窗的受压变形状态，同时推导了观察窗光学角偏差和光学畸变的理论计算方法， 最后基于有限元模拟结果和理论方法建立了Matlab GUI 交互式光学角偏差计算界面。 结果表明，观察窗的变形程度以及观察视角均会影响观察窗的光学角偏差和光畸变，且观察窗的变形会导致其光学性能的下降。利用本文的理论计算方法和Matlab GUI 界面可以直观地对观察窗的光学性能参数进行计算与分析， 在观察窗设计阶段的光学性能预测环节有一定的应用价值。