分布式发电系统并网逆变器高稳态性能重复控制策略

陈 磊，符仕浩，成佳斌，杨兴武

（1.国网浙江海宁市供电有限公司，浙江 海宁 314400；2.上海绿色能源并网工程技术研究中心（上海电力大学），上海 200090）

0 引言

为应对能源危机和减小环境污染，分布式发电受到越来越多的关注[1-2]。其中，并网逆变器作为新能源与电网的接口，其地位非常重要，研究并网逆变器的控制策略具有重要意义。

为了提高并网电流质量，通常采用LCL 滤波器。LCL 滤波器对逆变器产生的高频开关频率次谐波具有更好的衰减作用，且所需的总电感量较L 滤波器小[3]。但LCL 滤波器存在谐振问题，已有大量文献讨论了LCL 滤波器的各种无源、有源阻尼策略[4-7]。其中，GCFAD（并网电流反馈有源阻尼）[6-7]仅需要检测并网电流，系统具有硬件成本低、可靠性高的优点，在工程上得到了广泛的应用。

分布式PCC（电网公共耦合点）处含有各种谐波，而滞环、PI（比例积分）[8]以及QPR（准比例谐振）[3]等传统控制策略对电压谐波的抑制能力偏弱，因此为提高并网电流质量通常采用重复控制策略[9-15]。

已有的分布式发电系统重复控制策略[9-15]通常将重复控制器的内模改进环节Q（z）取成小于1的常数（如0.95）[9-12]，或陷波滤波器（如0.25z-1+0.5+0.25z）[13-14]，或FIR（有限脉冲响应）滤波器[15]，均获得了优质的并网电流输出。但尚无文献详细探讨Q（z）取这3 种方案时，重复控制的性能差异（如谐波抑制能力强弱等）。

为此，本文首先对比分析Q（z）取上述3 种方案时重复控制对谐波的抑制能力。基于此，提出一种分布式发电系统的HSP-RC（高稳态性能重复控制）策略，控制器采用HSP-RC 与P（比例）控制串联的复合结构。本文的贡献在于，HSP-RC的内模改进环节Q（z）采用了IIR（无穷脉冲响应）滤波器，与3 种传统方案相比，Q（z）具有更平坦的通带和阻带内幅值衰减速度快的特点，因而对电网的中高次谐波（至20 次）具有更好的抑制效果。本文详细给出HSP-RC 的设计过程，并对比分析了Q（z）取3 种传统方案和IIR 滤波器时系统的稳定性。最后对所提控制策略进行仿真验证，结果表明，采用所提控制策略，电网的中高次谐波得到更有效的抑制，分布式发电系统输出的并网电流质量更高。

1 分布式发电系统拓扑及控制结构

分布式发电系统的拓扑及控制结构如图1 所示。图中：Vdc为直流输入电压，由光伏电池、风机等提供；L1，L2为滤波器的电感；C为滤波器的电容；R1和R2为滤波器电感支路的寄生电阻；Vi和i1分别为逆变器的输出电压和输出电流；ic为滤波电容电流；i2为并网电流；PCC 为分布式电网的公共耦合点；Ug为电网电压；Zg为电网的线路和变压器阻抗。控制系统使用锁相环获得与PCC 电压同步的并网电流指令。

图1 分布式发电系统拓扑及控制结构

逆变器的电流控制方式为HSP-RC 与P 串联的复合控制，LCL 滤波器采用GCFAD[7]法。

2 内模改进环节Q（z）对重复控制性能影响分析

重复控制的核心部分是内模环节，原始内模的连续域表达式如下：

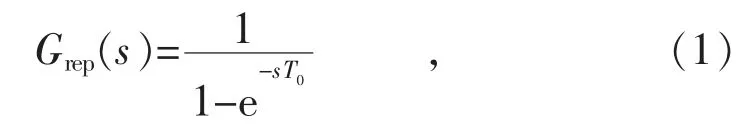
式中：T0为电网的基波周期。

由式（1）可得原始内模的极点为0，jω0，2jω0，…（其中ω0为基波角频率），因此原始内模可在基波和各次谐波频率处产生无穷大的增益。为提高系统稳定性，常采用改进的内模，改进内模的离散域表达式为：

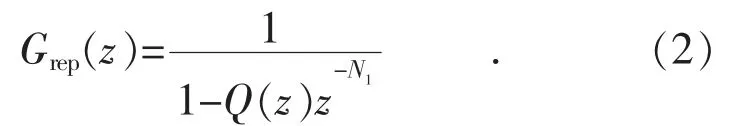
通常Q（z）可取为一个接近1 的常数、陷波滤波器或FIR 滤波器。Q（z）若取常数或陷波滤波器，则N1=T0/Ts（T0与Ts分别为电网的基波周期和采样周期）；若取FIR 滤波器，则N1=T0/Ts-d/2（d为FIR 滤波器的阶数）。

图2 给出了Q（z）取上述3 种方案时改进内模的幅频特性。其中陷波滤波器和FIR 滤波器的表达式如式（3）、式（4）所示，截止频率分别为1.84 kHz 和1.43 kHz。

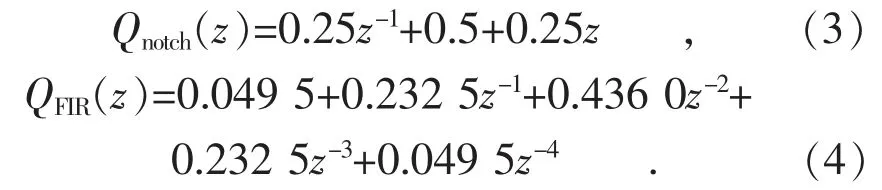
由图2 可知：在中低频段，Q（z）取陷波滤波器或FIR 滤波器时，基波和各次谐波频率处的增益较大；而取常数0.95 时，增益较小；在 高频段，增益的大小情况则相反。

造成上述现象的原因是：在中低频段，陷波滤波器或FIR 滤波器的幅频特性更接近1 p.u.，因此改进内模的谐振频率更接近0，jω0，2jω0，…，从而在基波和各次谐波频率处的增益较大。而在高频段，Q（z）取0.95，幅频特性更接近1 p.u.。

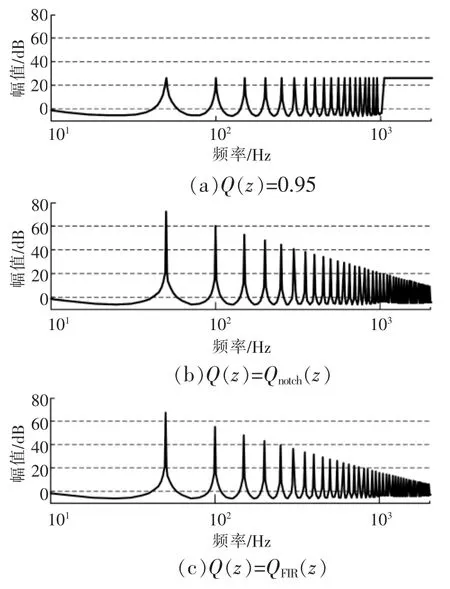
图2 改进内模幅频特性对比

由文献[14]可知，谐波频率处增益越大，谐波抑制的效果越好。因此，Q（z）取上述3 种方案时，不能兼顾低次谐波和中高次谐波的抑制。

3 HSP-RC 设计

3.1 HSP-RC 设计

以α 轴电流控制为例，HSP-RC 闭环系统结构如图3 所示。图中，P（z）为重复控制的等效控制对象，即仅P控制时的闭环传递函数，其表达式同文献[14]；Q（z）为内模改进环节；为延时环节，其中N2=T0/Ts；S（z）为低通滤波环节或低通滤波与陷波滤波的组合环节[14]；zm为相位超前环节，用来补偿P（z）及S（z）带来的相位滞后。

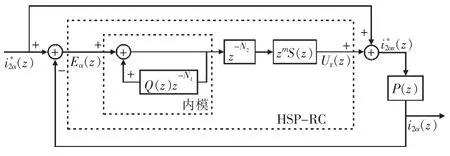
图3 HSP-RC 闭环系统结构

HSP-RC 设计主要针对内模改进环节Q（z）进行，而S（z）和超前环节zm的设计同文献[14]。

由第2 节的分析可知，要使改进内模的谐振频率接近电网谐波频率，Q（z）的截止频率应尽可能高。另一方面，为保证系统稳定，Q（z）在高频段应具有较快的幅值衰减速度。

为使Q（z）兼具截止频率高和高频段幅值衰减速度快这两种特点，本文提出一种新方法，即利用四阶线性相位IIR 滤波器作为Q（z）。IIR 滤波器的表达式为：

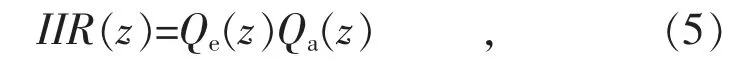
式中：Qe（z）和Qa（z）分别代表二阶椭圆滤波器和二阶全通滤波器。

椭圆滤波器在通带内幅频特性较平坦，因此在与FIR 滤波器阶数相同的情况下，其截止频率较高，且在阻带内拥有较快的幅值衰减特性。而级联全通滤波器的目的是使Qe（z）Qa（z）具有线性相频特性，这两个环节带来的相位滞后，在一定的频段内，可由超前环节zk精确补偿。

本文Qe（z）的截止频率取2 kHz，稍大于LCL滤波器的谐振频率fres（1.78 kHz），通带纹波取0.02 dB，由Fdatool 工具箱可得Qe（z）的表达式：

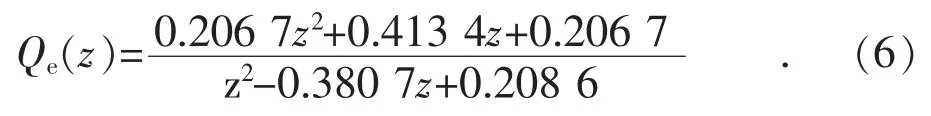
为使IIR（z）具有线性相频特性，经调试，全通滤波器Qa（z）取为：

相位补偿环节zk取z5，故N1取195。图4 示出了Qnotch（z），QFIR（z）z2和IIR（z）z5的伯德图。

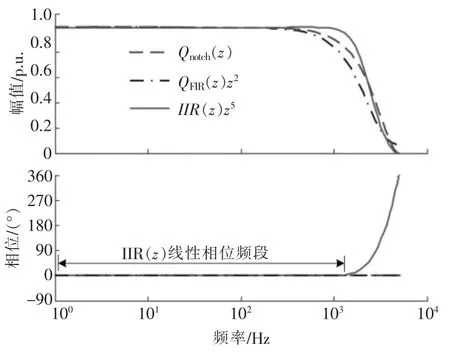
图4 伯德图对比

由图4 的幅频特性可知：陷波滤波器和FIR滤波器在通带内不如IIR 滤波器平坦，故改进内模的谐振频率只能精确至6ω0；IIR 滤波器在通带内平坦的幅频特性使得HSP-RC 内模的谐振频率可精确至20ω0；IIR 滤波器在阻带内的幅值衰减速度比陷波和FIR 滤波器都快，可保证系统的稳定性。由相频特性可知超前环节z5可以在1.5 kHz 内对IIR 滤波器带来的相位滞后进行精确补偿，即IIR 滤波器在1.5 kHz 以内具有线性相频特性。

由图3 得系统对指令信号的误差传递函数：

式中：Ea（z）为误差信号；为指令信号。

Q（z）取4 种不同方案时，系统跟踪给定误差的频率特性如图5 所示。

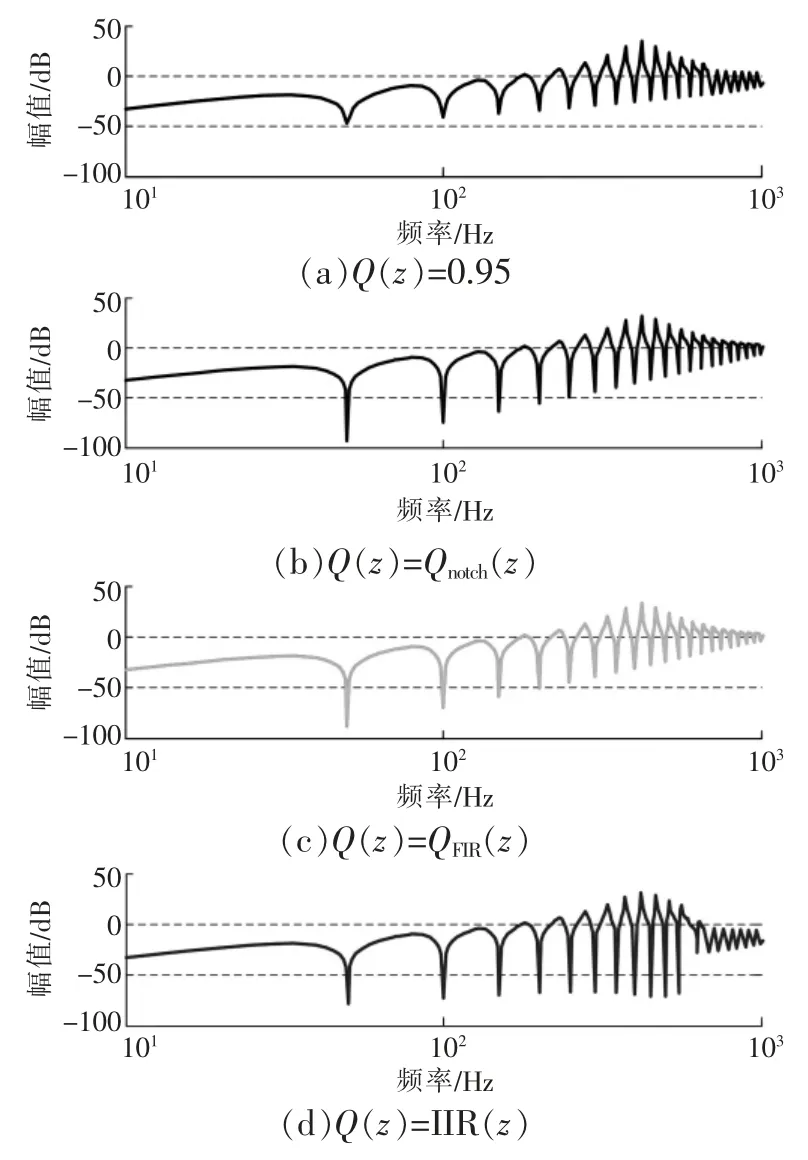
图5 跟踪误差频率特性

由图5 可知：与Q（z）取常数、陷波滤波器或FIR 滤波器相比，Q（z）取IIR 滤波器时3 次及以上谐波频率处的衰减增益均有较大降低，因此HSP-RC 可更有效地抑制电网的中高次谐波。

3.2 系统稳定性分析

闭环系统能够稳定的充分条件是系统特征方程根分布在单位圆内，由式（8），即：

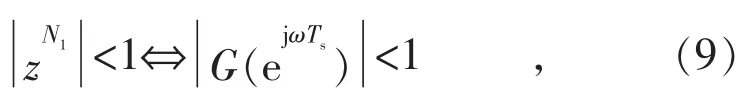
其中，

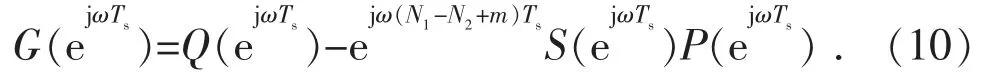
ω∈[0，π/Ts]，即角频率ω 从0 增大到奈奎斯特频率过程中，的轨迹不超过单位圆，可认为闭环系统的极点分布在单位圆内。Q（z）取4 种不同方案时的轨迹如图6 所示。

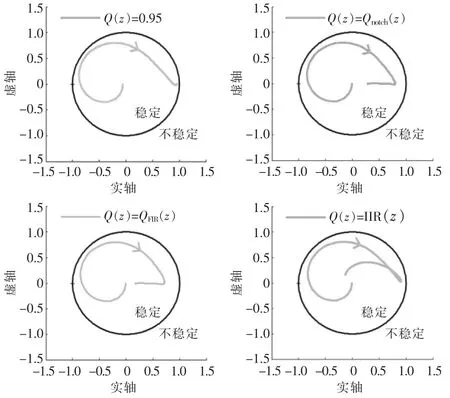
图6 轨迹

由图5、图6 可知：Q（z）若取陷波滤波器或FIR 滤波器，系统对低次谐波的抑制能力较强，而对高次谐波的抑制能力较弱，但闭环系统的稳定裕度较高；Q（z）若取常数，系统对低次谐波抑制能力较弱，而对高次谐波的抑制能力有所提高，但系统稳定裕度较低；Q（z）取IIR 滤波器时，系统对低次谐波和高次谐波均具有较强的抑制能力，且系统具有可观的稳定裕度。

4 仿真验证与分析

为验证上文理论分析的正确性以及所提控制策略的有效性，在MATLAB/Simulink 仿真环境下对HSP-RC 的控制性能进行了仿真研究。仿真参数：直流侧电压250 V，电网线电压有效值110 V，电网频率50 Hz，L1=4 mH，L2=1 mH，C=10 μF，采样频率10 kHz。

由于实际中PCC 电压含有各次谐波，因此仿真中向电网注入5，7，11，13，17，19 次谐波。图7 给出了PCC 电压以及Q（z）取4 种不同方案时并网电流的稳态仿真波形。图8 给出了稳态时A 相PCC 电压和并网电流的频谱。

图7 PCC 电压和并网电流稳态仿真波形

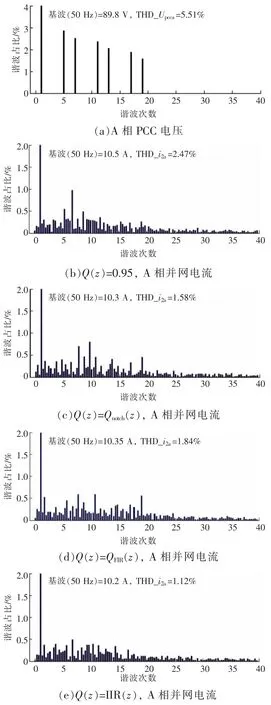
图8 A 相PCC 电压和并网电流频谱

由图7、图8 可知：Q（z）取4 种不同方案时均可使逆变器输出单位功率因数的并网电流，且并网电流的THD（总谐波畸变）均小于5%；Q（z）若取常数，并网电流的低次谐波含量较高，而高次谐波含量较低；Q（z）取陷波滤波器或FIR 滤波器时并网电流中的低、高次谐波含量与Q（z）取常数时相反；Q（z）取IIR 滤波器，并网电流中的低次谐波和中高次谐波含量均很小，并网电流质量最高。

5 结论

（1）所提HSP-RC 利用四阶线性相位IIR 滤波器替代传统方法的陷波滤波器、FIR 滤波器或者常数作为内模改进环节Q（z），该方法能够提高对电网的中高次谐波的抑制效果。

（2）采用所提控制策略，系统具有优良的稳态性能、较强的中高次谐波抑制能力、优质的并网电流输出。可见该控制策略在分布式发电系统中具有良好的推广价值。