基于仿真及物理模型试验构建圆形断面管道非满流流速函数

丁法龙，茅泽育，韩 凯

·农业水土工程·

基于仿真及物理模型试验构建圆形断面管道非满流流速函数

丁法龙，茅泽育，韩 凯

（清华大学水利水电工程系，北京 100084）

明渠断面流速分布是精确测量明渠断面流量的基础，也是明渠水流运动规律研究的基本问题。为探究圆形断面管道非满流的断面流速分布特性，采用经实测资料验证的三维紊流数学模型及数值求解方法，对不同底坡和充满度组合情况下的圆管非满流进行了数值模拟。结果表明：圆管非满流的断面流速分布对充满度非常敏感，充满度越大，垂线流速的非单调性越明显，当充满度低于0.5时，未出现最大流速点下潜（dip）现象；当充满度超过0.5时，dip现象越发明显，这是因为当充满度超过0.5后，内凹型侧壁对水面的约束作用增强，断面二次流更加明显。圆管非满流断面上各垂线的流速分布曲线具有很好的相似性，均接近于抛物线曲线特征，二次函数中的待定系数主要受垂线横向位置和充满度的影响。通过回归分析建立了圆管无压均匀流中沿垂线流速的抛物线分布公式，同时给出了各系数的确定方法，按上述流速分布律计算的流速值与实测值吻合良好，曲线拟合的决定系数均在0.92以上，表明给出的抛物型垂线流速分布规律是合理可靠的。

流量；流速；管道；圆形；非满流

0 引 言

圆形断面管道因具有较好的受力性能及便于预制和运输等优点，被广泛应用于人工管渠、输水涵洞、城市雨洪管道等灌溉和给排水工程中，出于对通风、防爆、排除有害气体以及适应水量变化等问题的考虑，在设计时通常将圆管内水流设计为非满流[1]，水体的上部边界与大气直接接触，管道非满流由重力主导，本质上属于明渠流动。

明渠断面流量的精确测量是引、排水工程中必须要解决的技术问题，也是进行水资源优化配置的基础。工程实际中，明渠均匀流流量计算常采用曼宁公式，它对于常规的折线形断面明渠具有一定的精确度，但却明显不适用于圆管非满流水力计算。根据圆形断面的几何关系，结合曼宁公式，可得过水流量关于糙率、充满角、圆管直径、底坡的表达式[1]。分析该式的函数极值，可知圆管非满流的流量随充满度（或充满角）的增加呈先增加后减小的非单一性变化，即流量最大值出现在充满度为0.94时的非满流状态，而不是恰为满管流时，这与实际情况相悖，因为实际使用的圆形断面管道，当底坡、糙率、管径一定时，过水断面流量随水深的增加单调递增[2]。

从曼宁公式本身角度进行分析，该双值性现象可解释为：曼宁公式以水力半径作为衡量断面过流能力的几何指标，但由于圆形断面形状的特殊性，超过一半水深后壁面逐渐内凹，则当充满度达到某一值后，断面湿周的增速要大于过流断面积的增速，二者的比值即水力半径逐渐减小，随充满度（即水深与管径的比值）的双值性变化导致了流量随亦呈现双值性变化，故对于圆形断面管道非满流，曼宁公式无法体现其真实流动特性。

明渠断面流速分布长期以来是工程水力学研究的热点问题，在曼宁公式等流量估算公式不适用的情况下，要精确测量明渠断面流量，无论是采用流速-面积法，还是采用流速-水位法，均需准确掌握明渠断面的流速分布。圆管明渠水流的自由水面不受固壁约束，流态容易受到管道断面几何特征、管道壁面粗糙程度及管道底坡等相关因素的影响，因此比圆管有压流复杂很多[2]；另外，相较于矩形、梯形、三角形等折线形断面明渠及抛物形的天然河道，由于受横向内凹型曲率壁面的影响，圆管非满流断面流速分布呈现更为显著的三维性，典型表现为垂线最大纵向流速点出现在水面以下的dip现象。

对于圆形断面明渠流速分布的研究，国内鲜见报道，国外研究则主要以鱼道和涵管为研究对象，以宽浅明渠中的垂向流速对数律为基本分布模型，并针对外区流速值偏离对数曲线的现象，采用尾流函数加以修正，修正后的对数-尾流律成为接受度最高的垂线流速分布形式[3-6]。但这种垂线流速分布形式在应用时存在明显的局限性，如公式中涉及的积分常数取值存在异议[7-8]；尾流强度系数的影响因素众多，具体取值不易确定[9]，且对数函数在应用中也存在不便，遇到积分时，往往因原函数无法确定，使得其应用范围受限，渠底流速和流速梯度为无穷大，不能反映侧壁处的流速分布[10]。除公式形式自身的缺陷外，垂线流速分布的对数-尾流律未考虑边壁的影响，分析水槽试验和数值计算结果，实际的垂向流速分布与对数-尾流曲线相比较，靠近中心区域的相关系数较高，但边壁区域的相关系数较小。

综上，曼宁-谢才公式未考虑圆形断面独特的边壁几何形态，不能很好地阐述流量随水深呈非单一性的变化；用于描述垂线流速分布的对数律及其衍生形式在应用时又产生诸多局限性。因此，研究圆管无压流动断面流速分布特性，对于丰富明渠水动力学理论，指导相关工程设计具有重要意义。通过试验确定明渠尤其是闭合断面明渠的流速分布，需要耗费大量时间且数据量有限，数值模拟是种便捷的替代方式。针对圆形断面管道无压均匀流进行了数值模拟，将数模结果与物理模型试验结果进行比较，验证数模及计算参数的合理性，并利用验证后的模型开展系列数值试验，研究了圆管无压均匀流的时均纵向流速的断面分布特性。

1 数学模型介绍

1.1 控制方程及紊流模型

圆形断面管道内的非满水流，可简化为图1所示的流动，该流动属于三维不可压缩流动，可由以下连续方程和动量方程（Navier-Stokes方程）来描述

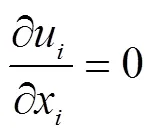
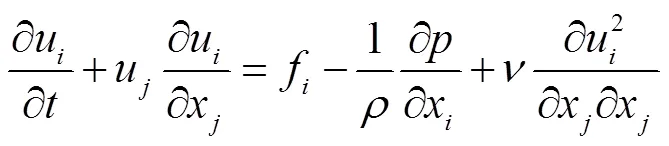
式中为流体密度，kg/m3；u、u为流速分量（m/s），=1,2,3、=1,2,3；x、x为坐标分量；为压强，Pa；f为质量力，N/kg；为运动黏性系数，m2/s。

工程实际中的明渠水流绝大多数为紊流，本研究采用雷诺时均（Reynolds averaged N-S）的数值模拟方法对时均N-S方程组进行求解，需选取合适的紊流模型封闭方程组。国内外研究表明，在窄深式断面明渠中，侧壁和水面的影响使水流结构呈现三维性[11-15]，同宽浅明渠相比，最为直观的区别就是，受第2类二次流的影响，过流断面上垂线最大流速点出现在水面以下，即最大流速下潜（dip）现象[16-19]。同一般的窄深式明渠水流类似，圆形断面明渠中也有该现象发生，但受内凹形侧壁形态的影响，圆形明渠中二次流形态有其独特性，有研究[20-21]表明，与折线形断面明渠相比，圆形断面明渠的二次流不存在底涡，仅由1对主涡组成，主涡的位置、大小和强度与渠道充满度有关，该主涡在水面附近将侧壁处低流速水体输运至中部，将表层高流速水体输运至水面以下，使最大流速下潜，由于没有底涡的存在，圆形明渠中出现最大流速下潜（dip）现象时，最大流速位置更低。

第2类二次流是由于雷诺应力的各向异性产生的，因此，为了准确模拟第2类二次流对断面流速分布的影响，应采用各向异性的紊流模型。RNG-模型是根据张量不黏性理论提出的非线性-紊流模型，与线性的标准-模型相比，RNG-模型能够准确地预测各向异性紊流[22-23]。因此，本研究采用RNG-模型封闭雷诺方程组，对圆形断面管道非满流特性进行数值模拟研究，湍动能输运方程和湍动耗散率输运方程如下[23]：

式中eff=+，为流体动力黏性系数，N·s/m2；为流体涡黏度，N·s/m2；G为由于平均速度梯度引起的湍动能产生项，m2/s2；一般4个经验常数的取值==1.39，1=1.42，2=1.68[16]。

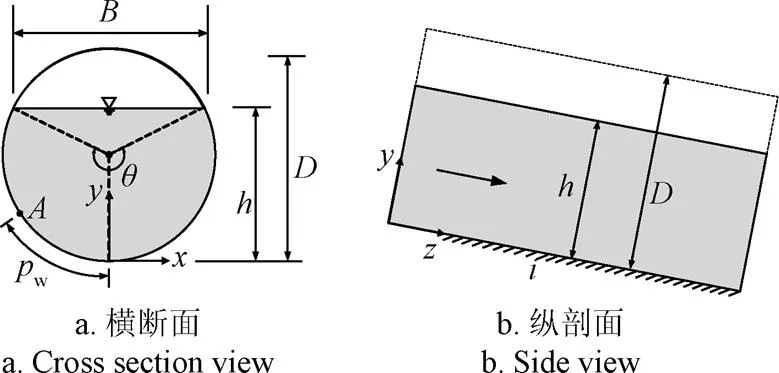
注：B为水面宽度，m；h为水深，m；D为管道直径，m；q为充满角；i为底坡；pw为边壁某点距离管道底部中点的湿周距离，m；x、y、z分别为展向、垂向和纵向坐标；A为边壁上某一点。

1.2 边界条件及数值方法

数值计算的边界条件及解算方法为：圆形断面管道上游进水边界条件设置为流量入口，给定相应的入口流量值；下游出水边界条件为自由出流（outflow），下游空气出口边界条件为给定大气压力值105Pa；为了考虑空气对水流流速的影响，自由水面的处理摒弃了明渠均匀流模拟常用的“刚盖”假定方法，采用Tru-VOF方法计算自由界面的水体体积率函数方程，该方法相较于传统的VOF方法很大程度上减少了模型收敛所需时间，可以准确地追踪水流自由表面变化的情况[24]；壁面边界条件为无滑移固壁条件，通过设置壁面颗粒的平均凸起高度k来量化管壁粗糙程度，并由标准壁面函数来确定壁面附近流速分布。

网格划分采用FAVOR（fractional area/volume obstacle representation）技术，这种方法对于复杂边界的流动区域，可以用平滑变化的六面体结构化网格进行离散，可高效解决网格模型失真问题[25]。计算域过流断面的网格尺寸设为0.01 m，横向垂向基本相同；沿流动方向网格尺寸为0.05 m。FAVOR技术采用有限差分法离散控制方程为代数方程组并进行数值求解，动量方程中对流项的离散格式采用二阶迎风格式，扩散项采用二阶中心差分格式，湍动能和湍动能耗散率的离散格式均采用二阶迎风格式；计算残差值设为10-6，时间步长在计算过程可自动调节，并限定最小时间步长为10-6s以保证数值稳定性；坡度对水流的影响通过将重力分解为纵向和垂向分量来体现。

建立管径0.4 m、管长50 m的圆管无压流动几何模型，针对3种不同底坡与12种不同充满度（即水深与管径的比值），共计36种工况条件的圆管无压均匀流进行数值计算，具体工况参数及网格划分情况见表1。

表1 数值计算的工况参数

2 物理模型试验介绍

为验证上述数学模型及其计算参数的可靠性，针对圆管明流的断面流速分布进行了室内测量试验。测流试验在长20 m、直径0.4 m且顶部开敞（距顶部4 cm以上部分被切割掉）的圆形断面有机玻璃质水槽中进行，水槽底坡=0.004，试验系统布置如图2所示。

图2 试验布置图

通过流量控制阀给定不同的首部流量，为保证边界层充分发展并尽快形成均匀流条件，在水槽进口和出口分别布置隔离板以减小水面波动，选取距离水槽首部15 m处为量测断面，根据流速分布的对称性，自中垂线向右等距平移2 cm设置测速垂线，每条垂线上自水面向下等距降低2 cm布置测点，试验水温在16 ℃左右。采用Nortek AS公司生产的Vetrino小威龙三维点式多普勒声波流速仪测量断面流速，测流用的探头类型为侧视（平视）探头，流速采样频率为25 Hz，每个测点收集100个数据，以其算术平均值作为该点的时均流速值；断面水深使用SCM60型水位测针测量，精度为0.1 mm；流量采用HFT多普勒流量计测量，测量精度为±0.5%。

3 结果与分析

3.1 数学模型验证

流速是分析水流运动规律的最基本要素，紊流的内部结构、能量传递过程及阻力特性等各种动力要素均与流速分布相关或以流速分布体现[26-29]，对比时均纵向流速的计算值与实测值，可以验证数学模型及相关参数的可靠性。物理试验结果及数值模拟结果的对比，前提是保证2种流动过程的边界层充分发展且已形成均匀流，因此，按照以下方式分别确定物理试验和数值模拟中的均匀流断面，进行运动要素的对比：1）物理试验中，分别选取距离首部13、14、15、16、17 m的5个过流断面，每个断面上按照上文所述布置测点，通过对比5个不同断面上相同对应位置的测点的平均流速值发现，在各个充满度条件下，5个断面上各对应点的最大相对差值均在1.26%以内，可认为5个不同的断面上具有相同的断面流速分布廓线，即此时已经形成均匀流。2）数值模拟中，分别在后处理中截取距离首部28、29、30、31、32 m的5个过流断面，每个断面上按照上文所述布置测点，通过对比5个不同断面上相同对应位置的测点的平均流速值发现，在各个充满度条件下，5个断面上各对应点的最大相对差值均在0.73%以内，可认为5个不同的断面上具有相同的断面流速分布廓线，即此时已经形成均匀流。由上述可知，物理试验中距首部15 m处的过流断面前后和数值模拟中距首部30 m处的过流断面前后均已形成均匀流，可以就该2个断面进行物理试验和数值模拟的结果比对。表2为底坡0.004、管径0.4 m、流量=0.246 m3/s（对应充满度=0.47）时，过流断面不同垂线上的时均纵向流速计算值与实测值对比。由表可见，纵向时均流速计算值与实测值的相对误差均在±4.2%以内，表明上述数学模型及其参数对于模拟过流断面的时均纵向流速分布具有较高的计算精度。

紊动能是表征紊流紊动特性的重要参数，运用Vectrino（小威龙）声学多普勒流速仪可以测量了各个流速测点的脉动流速，从而得到实际的紊动能大小；在RNG-两方程模型中，紊动能是基本未知量，可以直接求解得到。底坡0.004、管径0.4 m、流量=0.246 m3/s（对应充满度=0.47）时，过流断面不同测点的对比，见表2，紊动能计算值与实测值之间的相对误差均在±4.85%以内，表明该数学模型及参数选取对于模拟圆管明流的紊动特性亦有较高的精度。

3.2 圆管无压流动模拟结果

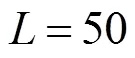
3.2.1 断面流速分布

圆管明渠水流流态受侧壁影响较大，断面流速分布呈现明显的三维性，图3所示为底坡=0.001 5、=0.75条件下，距管首30 m处过流断面的流速等值线图，由图可见，最大流速点出现在半水深以下，dip现象显著，对比所有工况的断面流速分布等值线图发现，当充满度低于0.5时，基本没有出现dip现象；当充满度超过0.5时，dip现象越发明显，这是因为当充满度超过0.5后，内凹型侧壁对水面的约束作用增强，断面二次流更加明显。图3中断面流速沿中垂线对称分布，近壁区的流速等值线基本平行于边壁，其他各工况亦有类似规律，与充满度大小无关。

表2 不同垂线位置及相对水深条件下均纵向流速和紊动能计算与实测值及相对误差

注：管径0.4 m、底坡0.004、充满度0.47、流量为0.246 m3·s-1。

Note: Pipe diameter 0.4 m, slope 0.004, filling ratio 0.47 and flow rate 0.246 m3·s-1.

3.2.2 垂线流速分布

为便于工程计算应用，通常把明渠断面流速分布的分析归结为垂线流速分布分析（如对数律、对数-尾流律亦是描述垂线流速分布），将垂线流速分布沿横向进行面积积分即可得到明渠断面流量。图4为=0.004，不同充满度时的断面中垂线流速分布，可见圆管非满流的垂线流速分布曲线对过流断面形式非常敏感，充满度越大时，垂线上的流速沿水深越呈非单调变化趋势，即最大流速点的dip现象越明显，这与断面流速等值线图的分析结果一致。

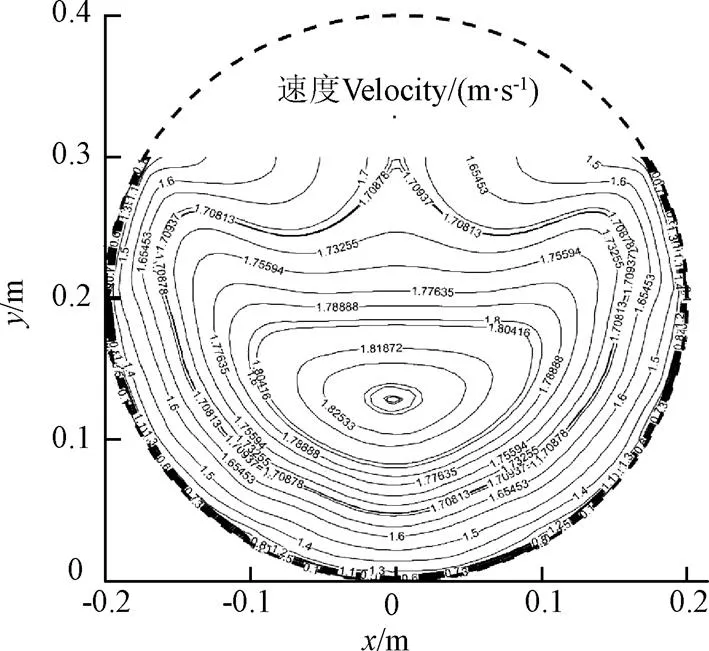
注：以过流断面中垂线最低端为原点，沿水流展向向右为x轴，沿水深方向向上为y轴。

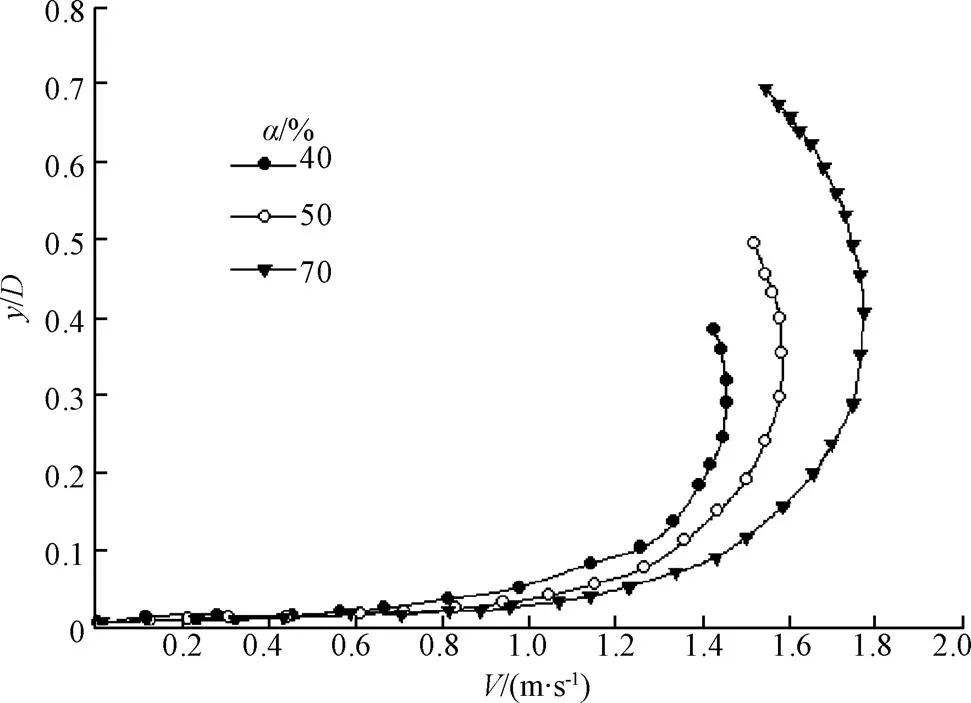
注：D为管道直径，m；y为垂向坐标，m；V为断面平均流速，m·s-1；a为充满度，下同。

图5为=0.004、=0.7条件下，不同横向位置处垂线上的流速分布，由图可见，不同横向位置处的垂线流速分布形式存在差异，尤其是靠近边壁区域的垂线，这是由内凹型侧壁对紊动水体的约束作用增强所致。

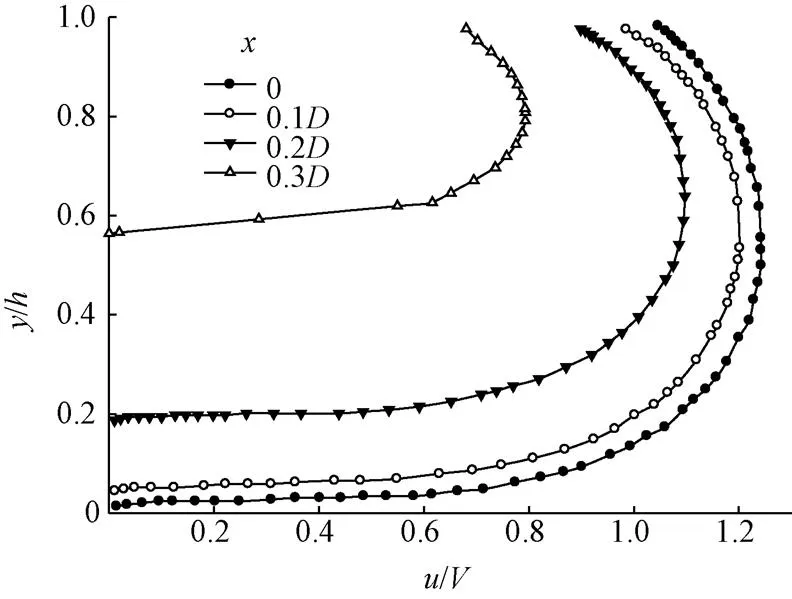
注：h为水深，m；u为点的时均流速，m·s-1。

3.2.3 垂线流速分布拟合分析

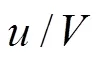
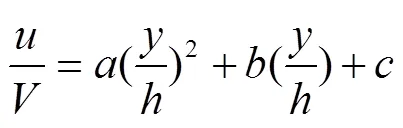
式中为过流断面平均流速，m/s；，，为待定系数。

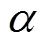
由于时均纵向流速以中垂线为轴呈对称分布，现只分析中垂线右侧即>0的情形。根据系数、、在不同的流动区域受和的影响程度不同，将过流断面沿横向划分为中心区和边壁区，其中：1）当<0.5时，≤2/5为中心区，>2/5为边壁区；2）当≥0.5时，≤/3为中心区，>/3为边壁区。方差分析结果表明，中心区的系数、、与横向位置和充满度均呈线性相关关系，而边壁区的系数、、则主要受垂线横向位置的影响，而与充满度基本无关。通过回归分析，得到不同流动区域中待定系数、、与充满度和垂线所在的横向位置之间的函数关系，如表3所示，其适用条件为0.10≤≤0.95，0.001 2 m3/s≤≤0.527 m3/s。

表3 待定系数a，b，c的拟合函数关系式

抛物型流速垂向分布律可以较为准确地反映圆管无压均匀流中的流速分布，且抛物线函数形式简单，便于工程实际应用，在准确掌握了圆管非满流流速分布规律后，就可以通过量测过流断面上特征点流速来确定垂线平均流速和断面平均流速，从而比较精确地计算圆管非满流的过水流量。

4 结 论

采用经实测资料验证的三维紊流数学模型及数值求解方法，对不同底坡和充满度组合情况的圆形断面管道无压流动进行了数值模拟，主要结果及结论如下：

1）在玻璃材质管径为0.4 m、底坡为0.004、流量为0.246 m3/s（对应充满度为0.47）条件时，过流断面不同垂线上的时均纵向流速计算值与实测值的相对误差均在±4.2%以内，表明数学模型及其参数对于模拟过流断面的时均纵向流速分布具有较高的计算精度。

2）圆管非满流的断面流速分布对充满度非常敏感，充满度越大，垂线流速的非单调性越明显。当充满度低于0.5时，基本没有出现dip现象；当充满度超过0.5时，dip现象越发明显，这是因为当充满度超过0.5后，内凹型侧壁对水面的约束作用增强，断面二次流更加明显。

3）圆管非满流断面上各垂线的流速分布曲线具有很好的相似性，均接近于抛物线曲线特征，二次函数中的待定系数主要受垂线横向位置和充满度的影响。

4）通过回归分析建立了充满度0.10≤≤0.95条件下圆管无压均匀流中沿垂线流速的抛物线分布公式，同时给出了各系数的确定方法，按上述流速分布律计算的流速值与实测值吻合良好，曲线拟合的决定系数均在0.92以上，表明给出的抛物型垂线流速分布律是合理的。抛物型分布律能较好地体现圆管非满流的垂线流速分布规律，采用垂线流速的抛物型分布律计算断面流量，既克服了采用曼宁公式计算流量时流量随充满度呈双值变化的不合理性，又比函数形式繁琐、不易积分求解流量的对数律衍生公式更易用于工程计算。

[1] 茅泽育，赵璇，罗昇. 圆形断面管道非满流流速计算表达式[J]. 水科学进展，2007，18(2)：170－174.

Mao Zeyu, Zhao Xuan, Luo Sheng. Analytic xepression for partially-filled flow velocity in pipe in of circular section[J]. Advances in Water Science, 2007, 18(2): 170－174. (in Chinese with English abstract)

[2] Guo J. Modified log-wake-law for smooth rectangular open channel flow[J]. Journal of Hydraulic Research, 2014, 52(1): 121－128.

[3] Rafik Absi. An ordinary differential equation for velocity distribution and dip-phenomenon in open channel flows[J]. Journal of Hydraulic Research, 2011, 49(1): 8.

[4] Clark S P, Toews J S, Tkach R. Beyond average velocity: Modelling velocity distributions in partially filled culverts to support fish passage guidelines[J]. International Journal of River Basin Management, 2014, 12(2): 101－110.

[5] Morrison, Ryan R, Hotchkiss, et al. Turbulence characteristics of flow in a spiral corrugated culvert fitted with baffles and implications for fish passage[J]. Ecological Engineering, 2009, 35(3): 381－392.

[6] Steffler P M, Rajaratnam N, Peterson A W. LDA measurements in open channel[J]. Journal of Hydraulic Engineering, 1985, 111(1): 119－130.

[7] Salih Kirkgöz M, Mehmet Ardiçlioğlu. Velocity profiles of developing and developed open channel flow[J]. Journal of Hydraulic Engineering, 1997, 123(12): 1099－1105.

[8] 王殿常，王兴奎，李丹勋. 明渠时均流速分布公式对比及影响因素分析[J]. 泥沙研究，1998(3)：86－90.

Wang Dianchang, Wang Xingkui, Li Danxun. Comparison of time average velocity formula and analysis of impact factors on open channel[J]. Journal of Sediment Research, 1998(3): 86－90. (in Chinese with English abstract)

[9] Yang S Q , Lim S Y , Mccorquodale J A . Investigation of near wall velocity in 3-D smooth channel flows[J]. Journal of Hydraulic Research, 2005, 43(2): 149－157.

[10] George W K. Is there a universal log law for turbulent wall-bounded flows[J]. Philos Trans A Math Phys Eng Sci, 2007, 365(365): 789－806.

[11] 韩延成，徐征和，高学平，等. 二分之五次方抛物线形明渠设计及提高水力特性效果[J]. 农业工程学报，2017，33(4)：139－144.

Han Yancheng, Xu Zhenghe, Gao Xueping, et al. Design of two and a half parabola-shaped canal and its effect in improving hydraulic property[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(4): 139－144. (in Chinese with English abstract)

[12] Kundu S, Kumbhakar M, Ghoshal K. Reinvestigation on mixing length in an open channel turbulent flow[J]. Acta Geophysica, 2018, 66(1): 93－107.

[13] Minakshee Mahananda, Prashanth Reddy Hanmaiahgari, Balachandar R. Effect of aspect ratio on developing and developed narrow open channel flow with rough bed[J]. Canadian Journal of Civil Engineering, 2018, 45(1): cjce-2017-0458.

[14] Xia W, Chen H, Wang J, et al. Fractal characteristics of turbulent flows in open channel[J]. Journal of Hydroelectric Engineering, 2018. DOI:10.11660/slfdxb.20180705

[15] Vishal G, Tomar J, Bharti R P. Critical parameters for non-Newtonian power-law fluid flow across a channel confined circular cylinder[R/OL]. 2019. https://www.researchgate.net/ publication/330552989

[16] Momplot A, Kouyi G L, Mignot E, et al. Typology of the flow structures in dividing open channel flows[J]. Journal of Hydraulic Research, 2018, 55(1): 63－71.

[17] Anjum N, Ghani U, Pasha G A, et al. Reynolds stress modeling of flow characteristics in a vegetated rectangular open channel[J]. Arabian Journal for Science & Engineering, 2018(2): 1－8.

[18] Pu J H. Turbulent rectangular compound open channel flow study using multi-zonal approach[J]. Environmental Fluid Mechanics, 2018(3): 1－16.

[19] Bonakdari H, Frédérique Larrarte, Lassabatere L, et al. Turbulent velocity profile in fully-developed open channel flows[J]. Environmental Fluid Mechanics, 2008, 8(1):1－17.

[20] Zhu Z, Wang J, Yan C, et al. Experimental study on natural circulation flow resistance characteristics in a 3 × 3 rod bundle channel under rolling motion conditions[J]. Progress in Nuclear Energy, 2018, 107: 116－127.

[21] Keramaris E, Pechlivanidis G. Effects of different porous beds on turbulent characteristics in an open channel above the porous bed[J]. Flow Measurement & Instrumentation, 2017, 54: 20－26.

[22] 张春晋，孙西欢，李永业，等. 流固耦合作用对筒装料管道车水力输送内部流场特性的影响[J]. 农业工程学报，2018，34(18)：307－315.

Zhang Chunjin, Sun Xihuan, Li Yongye, et al. Effect of fluid-structure interaction on internal flow field characteristics of tube-contained raw material pipeline hydraulic transportation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(18): 307－315. (in Chinese with English abstract)

[23] 陈庆光，徐忠，张永建. RNG-模式在工程湍流数值计算中的应用[J]. 力学季刊，2003，24(1)：88－95.

Chen Qingguang, Xu Zhong, Zhang Yongjian. Application of RNG-models in numerical simulations of engineering turbulent flows[J]. Chinese Quarterly of Mechanics, 2003, 24(1): 88－95. (in Chinese with English abstract)

[24] 冉聃颉，王文娥，胡笑涛. 梯形喉口无喉道量水槽设计及其水力性能模拟与试验[J]. 农业工程学报，2017，33(15)：177－183.

Ran Danjie,Wang Wen'e, Hu Xiaotao. Design of trapezoidal cut-throated flumes and its hydraulic performance simulation and test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(15): 177－183. (in Chinese with English abstract)

[25] Huai W, Xue W, Qian Z. Large-eddy simulation of turbulent rectangular open-channel flow with an emergent rigid vegetation patch[J]. Advances in Water Resources, 2015, 80: 30－42.

[26] Stewart M T, Cameron S M, Nikora V I, et al. Hydraulic resistance in open-channel flows over self-affine rough beds[J/OL]. Journal of Hydraulic Research, 2018: 1－14. DOI: 10.1080/00221686.2018.1473296

[27] 刘晓东，韩宇，邱流潮，等. 基于平均紊动结构下明渠水流流速分布研究[J]. 灌溉排水学报，2018，37(8)：106－114.

Liu Xiaodong, Han Yu, Qiu Liuchao. Velocity distribution within open channel studied using the average structure of turbulent flow[J]. Journal of Irrigation and Drainage, 2018, 37(8): 106－114. (in Chinese with English abstract)

[28] 王文娥，薛城，胡笑涛. 沟灌三角形长喉道田间量水槽水力特性试验及数值模拟[J]. 农业工程学报，2019，35(3)：109－116.

Wang Wen'e, Xue Cheng, Hu Xiaotao. Numerical simulation and test of hydraulic performance for triangle long-throat flume for water measurement in furrow irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(3): 109－116. (in Chinese with English abstract)

[29] 李广宁，孙双科，郭子琪，等. 仿自然鱼道水力及过鱼性能物理模型试验[J]. 农业工程学报，2019，35(9)：147－154.

Li Guangning, Sun Shuangke, Guo Ziqi, et al. Physical model test on hydraulic characteristics and fish passing performance of nature-like fish way[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(9): 147－154. (in Chinese with English abstract)

Establishment of velocity function of partially-filled flow in circular pipe based on simulation and physical model experiment

Ding Falong, Mao Zeyu, Han Kai

(,,100084,)

Velocity distribution of cross-section in open channel is not only the basis of accurate measurement of flow rate, but also the basic problem of studying the hydraulic characteristics of open channel. In order to explore the cross-sectional velocity distribution of partially-filled flow in circular pipe, a 3-D turbulent mathematical model and numerical solution method, verified by measured data, were adopted to simulate the partially-filled flow in circular pipe with different combinations of slopes and filling ratios. By comparison of the measured values and calculated values, the results showed that in a circular pipe with diameter 0.4 m, bottom slope 0.004, and flow rate 0.246 m3/s (corresponding filling ratio 0.47), the maximum relative error between the calculated velocities and measured values on all vertical lines was within the plus or minus 4.2%, and the maximum relative error between the calculated turbulent kinetic energy and measured values on all vertical lines was within the plus or minus 4.85%, suggesting that mathematical model and its parameters for simulation of the velocity distribution had higher calculation accuracy. The simulation results showed that cross-sectional velocity distribution was very sensitive to the filling ratio. The larger filling ratio would lead to more obvious dip phenomenon of maximum vertical velocity. When the filling ratio was lower than 0.5, no dip phenomenon occurred. When the filling ratio exceeded 0.5, the dip phenomenon became more obvious. This was because when the filling degree exceeded 0.5, the constraint effect of the side wall on the water surface was enhanced, and the secondary flow in the section was more obvious. There also showed obvious differences in the forms of vertical velocity distribution at different transverse positions, especially those close to the boundary wall, which was caused by the enhanced constraint effect of the concave side wall. Vertical profiles of time-averaged longitudinal velocity among various cases had very good similarity, and the profile curves were close to the feature of parabolic function. Influenced by factors such as section geometry and hydraulic characteristics, although the velocity distribution of each vertical line had a good similarity, the empirical coefficients by parabolic regression analysis that determined the shape of the velocity distribution curve on the specific vertical line had changed a lot. Multi-factor analysis of variance was conducted to the undetermined coefficientsin parabolic function, which showed they were mainly affected by transverse position of vertical lines and filling ratio of cross section. According to the affecting degree of filling ratio and transverse position to the empirical coefficientsthe cross sections of the partially-filled flow were divided into the central areas and the side wall areas along the transverse direction. Moreover, the dividing lines between central area and side wall area when the filling ratio was less than 0.5 was different from that when the filling ratio was greater than 0.5. Analysis of variance showed that the empirical coefficients of the central area were linearly correlated with the transverse position and the filling ratio, while the coefficients of the side wall area were mainly affected by the transverse position of the vertical line, and basically independent of the filling ratio. By means of regression analysis, the velocity parabolic distribution formula on vertical lines in partially-filled flow were established, and the determination methods of each coefficients were given. The calculated values of vertical velocity distribution areas were in good agreement with the measured values, which indicated that the parabolic vertical velocity distribution law was reliable. Parabolic function could better reflect the velocity distribution along vertical lines of partially filled flow in circular pipe. Application of the parabolic function to obtain flow rate on cross section, cannot only overcome the irrationality of Manning formula, but also was more easier than logarithmic law to be used in engineering calculation.

flow rate; flow velocity; canals; circular; partially-filled flow

丁法龙，茅泽育，韩 凯. 基于仿真及物理模型试验构建圆形断面管道非满流流速函数[J]. 农业工程学报，2019，35(18)：55－61.doi：10.11975/j.issn.1002-6819.2019.18.007 http://www.tcsae.org

Ding Falong, Mao Zeyu, Han Kai. Establishment of velocity function of partially-filled flow in circular pipe based on simulation and physical model experiment[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(18): 55－61. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.18.007 http://www.tcsae.org

2018-12-13

2019-08-10

国家重点研发计划（2016YFC0402504）

丁法龙，博士，主要从事水力学及河流动力学方面的研究工作。Email：dflaizy@163.com

10.11975/j.issn.1002-6819.2019.18.007

TV93

A

1002-6819(2019)-18-0055-07