环境流体动力学模拟优选人工湿地设计中隔板湿地长度比

万 荻，崔远来，郭长强，马 震

环境流体动力学模拟优选人工湿地设计中隔板湿地长度比

万 荻1，崔远来1※，郭长强2，马 震1

（1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 浙江大学生物系统工程与食品科学学院，杭州 310058）

采用环境流体动力学模型（environmental fluid dynamics code，EFDC）建立表面流人工湿地水动力-水质耦合模型，研究隔板长度与湿地长度比值（简称隔长比）对表面流人工湿地水力性能及净化效果的影响规律，优选适宜的隔长比。结果表明：1）率定和验证的12组结果中，水动力模型模拟评价结果为中等及以上，即相关系数>0.7、纳什系数>0.4、相对误差<20%，的有7组，水质模型模拟评价结果为中等及以上，即相对误差<20%，的有10组。2）表面流人工湿地适宜隔长比随长宽比的增加而增大，当长宽比由1、2、4变为4、8、16时，对应的适宜隔长比分别为0.675、0.850、0.938。3）表面流人工湿地主要水力指标随适宜隔长比的增大而增加，对净化效果指标的提升不明显。4）在适宜隔长比不变的情况下增加湿地的表面积能明显提升水质净化效果（>50%）。研究可为表面流人工湿地实际工程设计提供依据。

水力性能；净化效果；优化；表面流人工湿地；隔长比；长宽比；EFDC模型

0 引 言

影响表面流人工湿地水力性能和净化效果的主要设计参数有长宽比、水深、流量、进出口布置、水力负荷、植物和隔板设置等[1-6]。目前国内外已有不少针对长宽比对水力性能及净化效果影响的研究。Thackston等[7]研究表明窄长的湿地具有较高的水力性能，随着长宽比增大，湿地的水力性能呈指数级增长。Koskiaho[8]发现隔板能有效地引导主流对湿地面积进行优化利用，大大提高了湿地的水力效率。朱永青[9]通过试验表明，增大长宽比对总磷的去除效率略有提升。蒲红杰等[10-11]均认为增大长宽比能有效提升湿地对污染物的净化效果。

开展表面流人工湿地水力性能和净化效果试验时，由于试验场地的限制，常常通过设置隔板来达到增大长宽比的效果[12]。Su等[13]通过增设隔板对湿地的水力效率进行了优化设计。Cui等[14]认为拥有隔板的湿地系统具有较好的混合流动方向和内部供氧能力，能有效去除化粪池废水中的氮和磷。实际工程设计中，对于较大长宽比的处理，往往基于较小长宽比的湿地通过在湿地宽边中部设置隔板来达到宽度（width，）减小一半，长度（length，）增大1倍，长宽比（aspect ratio，/）增至4倍的效果[15]。然而，目前鲜有研究针对湿地实际工程设计提出具体隔板设置方案。因此，确定合理的隔板长度或隔长比，使得通过隔板设置形成的较大长宽比的湿地（简称模型湿地）与实际长宽比湿地（简称实际湿地）水力性能和净化效果相近对实际工程设计具有重要意义。由于通过试验更改隔板长度工程量巨大，因此数值模拟是有效途径。

在众多数值模型中，环境流体动力学模型（environmental fluid dynamics code，EFDC）在水动力模拟方面具有较强的优势，在水质模拟方面，能够模拟藻、碳、氮、磷的转化过程[16]，已被广泛用于湿地[17-18]、湖泊[19-20]以及小型生态沟[21]等地表水的模拟及研究。

综上，本文基于表面流人工湿地示踪试验及水质净化效果试验的数据，率定和验证EFDC模型，开展不同长宽比条件下模型湿地与实际湿地的水动力及水质过程模拟分析，优选出不同情况下的隔长比，为表面流人工湿地优化设计和提升改造提供依据。

1 材料与方法

1.1 表面流人工湿地试验

试验区位于江西省赣抚平原区的江西省灌溉试验中心站表面流人工湿地试验基地内，试验小区由18个长6 m、宽4.7 m的小型试验池和2个长14.7 m、宽6.0 m的中型试验池及1个长14.7 m、宽6.0 m的蓄水池组成。本次试验基于混合水平的正交试验L16（44×23）设计，即4个四水平因素和3个二水平因素，共计16次试验，各设计因素水平分布见表1。根据试验设计方案对试验池进行形状改造，使其成为16个表面积均为18 m2的表面流人工湿地试验池（编号分别为1、2、…16），试验具体设计及处理参考文献[15]。

表1 表面流人工湿地正交试验设计因素水平

1.2 表面流人工湿地水力指标及水质指标

已有研究从众多的水力指标中筛选出了4个具有代表性、敏感性和稳定性的水力指标，分别为有效容积率（effective volume ratio，）、短路指标10、莫里尔离散指数（Morril dispersion index，MDI）和矩指数（moment index，MI）[22-24]。

根据试验方案，测定的水质指标包含总氮（total nitrogen，TN）和总磷（total phosphorus，TP）。因此，选取总磷浓度去除率TP和总氮浓度去除率TN为湿地净化效果指标[15]。

中值误差0.5（见式（1））用来评价2湿地各个指标之间的吻合程度，即水力性能和净化效果之间的接近程度[25]。

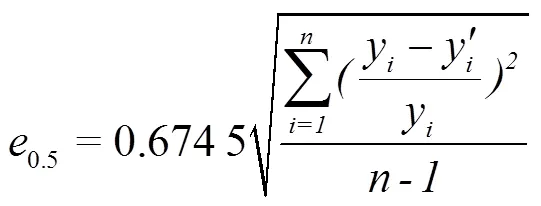
式中代表指标个数；，′（=1,2,…,）分别表示一组模型湿地的各水力、净化效果指标值和实际湿地的各水力、净化效果指标值。

1.3 模型评价标准

对于水动力模型，选取相关系数（correlation coefficient，）、纳氏系数（Nash-Suttcliffe coefficient）和相对误差（relative error，）为效率评价指标，根据系数的取值划分为4个评价标准：优、良、中、差[26]，见表2。

对于水质模型，由于水质净化效果试验采用每间隔一段时间取样监测的方式，不能获取类似示踪剂浓度自动监测的结果，数据点分散且不多，因此采用相对误差为判别标准。

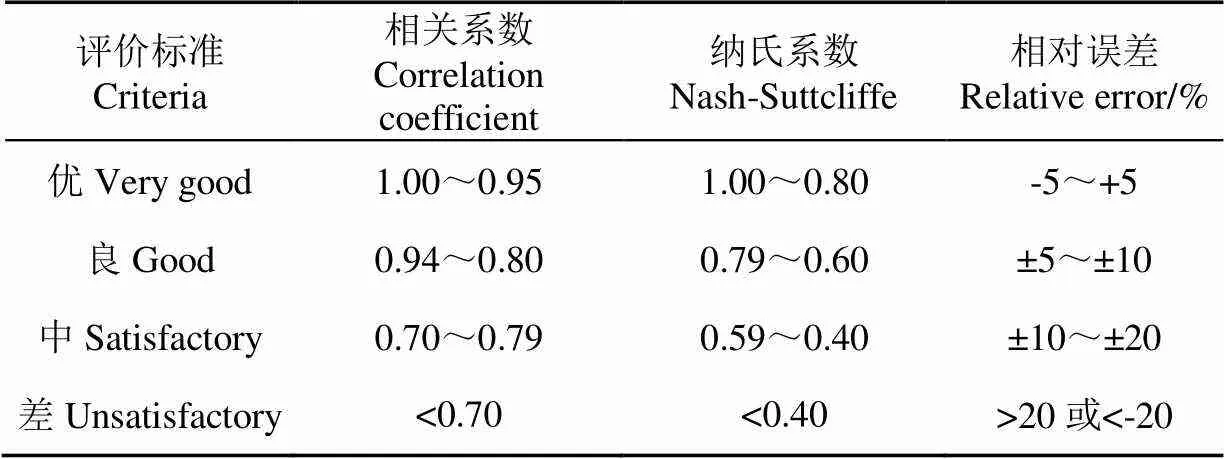
表2 水动力模型模拟效率评价标准

1.4 EFDC模型及参数率定方法

1.4.1 模型简介

环境流体动力学模型（EFDC）是一个开源的地表水模型，其由FORTRAN语言编写而成，在单一源代码框架下，耦合了水动力、水质与富营养化、泥沙输运、有毒化学物质输运与转化等子模块[16]。目前，EFDC已经在100多个地表水系统中得到广泛验证。EFDC模型水动力模块在水平方向和垂直方向分别采用曲线正交坐标变换和坐标变换。其基本方程是基于湍流方程的垂直流体静力边界层形式变换，利用变密度的Boussinesq近似得到，包含动量方程、连续性方程、状态方程、物质传输方程[27]。EFDC水质模块基于求解21个状态变量的质量平衡方程，用于模拟3组藻类、碳循环、氮循环、磷循环和硅循环、溶解氧和粪大肠菌群。本文采用该模型的水动力和水质模块来模拟表面流人工湿地的水动力及水质过程。

1.4.2 表面流人工湿地水动力-水质耦合模型构建

结合试验湿地尺寸，本次模型构建采用0.1 m × 0.1 m的矩形网格，为使模型运行稳定且不发生水流边界溢出，时间步长经多次调试取为0.1 s。模型的输入数据中水深、流量和植物资料等均来源于实测值，初始时刻水深即为设计水深。设置2种入流边界：与湿地同宽度的均匀进水入流边界，进水高度10 cm；在湿地宽边中间进水的入流边界，进水口宽20 cm，进水高度10 cm。出流边界位于湿地进水边对面的宽边中部，宽20 cm，高10 cm。模型通过调整分配系数对流量在宽度网格上的分配来设置两种入流边界。对于设置有隔板的湿地，将已修改格式的EFDC网格文件导入Delft-3D软件中，调整网格疏密使隔板区域网格宽度与隔板实际宽度相同（0.01 m），然后将从Delft-3D软件中导出的网格文件导入到EFDC模型中，通过修改dxdy文件，设置隔板高度为1 m。

1.4.3 模型参数率定和验证

通过表面流人工湿地的示踪试验数据及水质净化数据进行模型参数的率定和验证。进行参数率定时，根据经典案例及相关文献[28-32]先确定模型参数的初始值。通过敏感性分析，得到背景值/常数的涡流黏度、无量纲水平扩散系数、边壁糙率、底部粗糙度、最大硝化反应速率、硝化作用最适温度和底泥对磷酸根的吸收/释放通量为影响表面流人工湿地水动力及水质过程的敏感参数[33-34]。在此基础上，对敏感参数进行手动微调，当率定组湿地的模拟与实测过程总体吻合较好时确定参数取值，然后用验证组湿地数据验证模型。

1.5 模拟方案设置

本次模拟方案设置模型湿地和实际湿地2种湿地各6个，长和宽的设置见表3。均采用中进中出的流量边界，流量为0.85 m3/h，初始水深0.2 m。

表3 模拟方案设置

模型湿地设置隔板，实际湿地无隔板，实际湿地与模型湿地一一对应，即模型湿地1对应实际湿地7，模型湿地2对应实际湿地8，依此类推，其中实际湿地的长宽比为对应模型湿地的4倍。方案模拟的目的是通过对比模型湿地与实际湿地（见图1），找到使模型湿地的长宽比增至4倍的适宜隔长比。即对模型湿地进行多个隔长比的模拟，得到多组结果，并分别与实际湿地的模拟结果对比，其中与实际湿地的模拟结果最为接近的模型湿地对应的隔长比为适宜隔长比。

注：通过在模型湿地（长宽比1:1）中设置隔板达到与实际湿地（长宽比4:1）等效的目的。

2 结果与分析

2.1 水动力模块率定及验证结果

由于9～12号湿地由2个中型试验池改造得来，每个中型试验池里分隔出2个特定尺寸的湿地试验池，进行9～12号湿地试验时，位于同一个中型试验池里的2个试验湿地相互影响，使水深观测数据不准确。故本次模型研究仅利用另外12个单独湿地（1～8号和13～16号）的试验数据进行模型参数的率定及验证，其中1～8号湿地数据用于率定模型参数，13～16号湿地数据用于验证模型。水动力模块模型参数率定值如表4所示，率定组湿地的模拟和实测值的评价结果见表5，示踪曲线对比见图2。由率定组结果（表5）可知，4个评价结果为优或良（1、3、5、8号湿地），1个评价结果为中（2号湿地），3个评价结果为差（4、6、7号湿地）。评价结果为中的2号湿地的相关系数和纳氏系数均符合良好标准，仅相对误差较大。

表4 水动力模块模型参数率定值

注：本文研究对象为层流，雷诺数很小，相较于江河湖海等一般紊流水体，其AHO和AHD取值要小。

Note: Research object of this paper is laminar flow, and the Reynolds number is very small. Compared with general turbulent water bodies such as rivers, lakes and seas, the AHO and AHD values are smaller.

表5 水动力模块率定和验证结果

进一步分析率定期示踪剂浓度模拟结果（图2）可知，评价结果为优或良的湿地在曲线上升段、下降段、上升段起始点、下降段稳定点、峰值点均拟合的很好。评价结果为中的2号湿地仅仅是在上升段拟合不佳，且模拟值比试验值整体偏大，这可能是由于试验过程中示踪剂被湿地植物或基质截留导致回收率偏差，体现在评价结果上即显示相对误差值较大。评价结果为差的3个湿地中，有2个湿地（4号和6号）的试验示踪曲线都表现为上升段起始时间很小，上升段十分陡峭，斜率接近90°。这说明示踪剂在湿地中存在短路，即有1个快速通道使得示踪剂团很快到达出口，并使浓度快速到达峰值。而造成短路现象的原因很多，例如风的影响，中部植物种植疏于两侧植物等[35-37]。

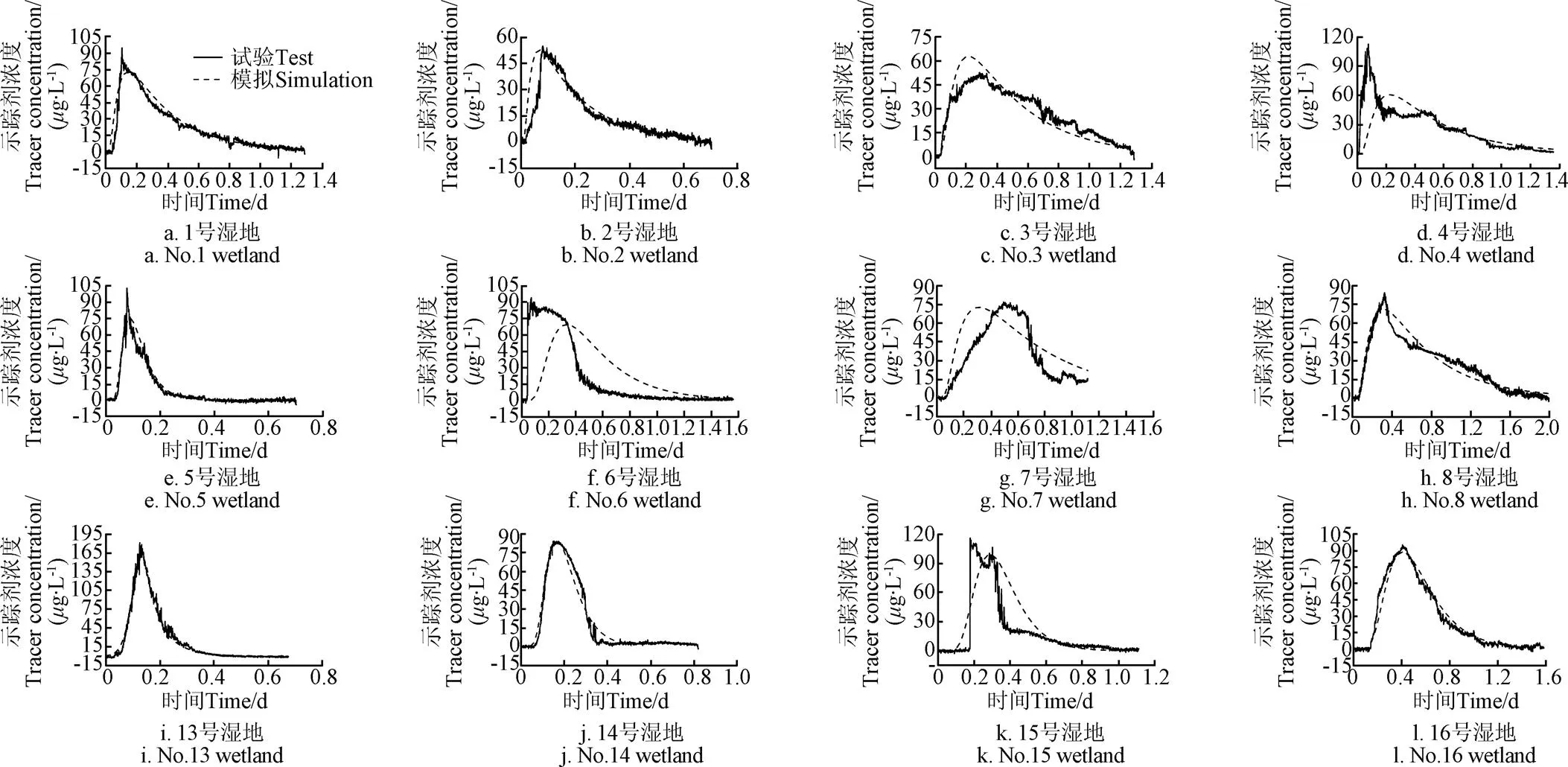
图2 率定和验证组湿地示踪剂浓度模拟结果

由表5知，水动力模型模拟评价结果为中等及以上，即相关系数>0.7、纳什系数>0.4、相对误差<20%，的有7组，仅1组评价结果为差，且评价结果为差的主要原因是相对误差值较大。验证期示踪剂浓度模拟结果（图2i～图2l）显示，评价结果为差的15号湿地，其示踪曲线出现了浓度异常升高和降低且存在双峰的现象，这与试验常识不符，分析可能的原因是YSI水质监测仪在试验过程中发生了位移，造成示踪剂浓度监测不灵敏，试验数据有误。

以上结果表明，构建的水动力模型可以用于表面流人工湿地水动力过程模拟。

2.2 水质模块率定及验证结果

水质模块模型参数率定值如表6所示，率定组湿地的模拟和实测值的评价结果见表7。

表6 水质模块模型参数率定值

同水动力模块一样，用1～8号湿地的水质数据率定，13～16号湿地水质数据验证模型。从表7可见，水质模型模拟评价结果为中等及以上有10组，即相对误差<20%。评价结果为差的湿地是4号及7号。其中4号湿地的实测去除率比模拟去除率高，且误差较大。这可能是由于湿地水流短路造成进入人工湿地的污染物快速到达出口，没有足够的时间被藻类或植物吸收、截留，或沉积到底部。而7号湿地的实测进出口去除率为负值，明显偏离实际情况，故将7号湿地的率定结果排除。参考前面的结果，4、7号湿地在水动力模块的率定中表现也很差，可能的原因也是由于短路造成水动力条件与预想的不符。这说明水动力模块率定结果中表现不佳的4、7号湿地在水质模块的率定中表现也很差，进一步证实了模拟值与实测值产生偏差是由于水流短路造成的。

综上，率定和验证的12组结果中，水动力模型模拟评价结果为中等及以上的有7组，水质模型模拟评价结果为中等及以上有10组，满足精度要求，故环境流体动力学模型可以用于表面流人工湿地水动力过程和水质过程的模拟。

2.3 不同情景的模拟分析

以模型湿地1为例阐述得到适宜隔长比的过程，4个水力指标有效容积率、短路指标10、莫里尔离散指数和矩指数和2个净化效果指标总氮浓度去除率TN和总磷浓度去除率TP作为模拟结果，模型湿地1共设置了14种不同的隔长比，根据每种隔长比下的模拟结果得到了14组模拟结果，见表8。

表7 水质模块率定和验证结果

实际湿地7的模拟结果为：=0.895、10=0.512、 MDI=2.669、MI=0.789、TP=33.59%、TN=35.56%。其中使得0.5最小的隔长比为适宜隔长比，即0.675（表8）。随着隔长比增大，有效容积率逐渐增大，并逐渐趋于稳定；10和MI逐渐增大，MDI逐渐减小。这说明4个指标具有较好的一致性，均反映了隔长比的增大能促进湿地水力性能的提升。此外，随着隔长比的增大，TP和TN逐渐增大，但是增幅很小，说明增大隔板长度对于提高湿地净化能力的效果不明显。对比1号湿地（长宽比1，面积16 m2）和5号湿地（长宽比4，面积16 m2）的水质指标也可得，改变长宽比对净化效果无明显影响。同样，郭长强等认为长宽比对湿地净化效果无显著影响[38]。Jong-Hwa等的试验也表明2:1和0.8:1长宽比的湿地对去除污染物磷的效果无明显差异[39]。

表8 模型湿地1不同隔长比下的水力及水质指标

注：由于各指标值不存在拐点，因此省去隔长比小于0.425和大于0.75的情况。

Note: Since there is no inflection point in each index value, we omitted results of obstruction length-to-wetland length ratio less than 0.425 and greater than 0.75.

同理得到其他5种模型湿地的适宜隔长比及适宜隔长比下的水力指标及水质指标值，见表9。

表9 各模型湿地的适宜隔长比及水力及水质指标值

对于相同长宽比不同面积的湿地（情景1、2，情景3、4，情景5、6），观察水力指标可得，面积对湿地水力性能的影响不大；观察净化效果指标可得，随着湿地面积增大，净化效果有着显著提升，这主要是由于面积的增大提高了湿地的水力停留时间，而足够的水力停留时间使得污染物能在水体中充分混合、反应、被吸收和利用。

传统试验设计或工程应用中，常常通过在湿地宽边中部设置长度为-0.5的隔板，来达到宽减小一半，长增大一倍，长宽比/增至4倍的效果。按照这样的设计方法，长宽比为1、2、4的湿地分别应设置的隔长比为0.5，0.75，0.875。而由表9知长宽比1、2、4下适宜隔长比分别为0.675、0.850、0.938，均比传统设计方法的取值要大，这说明采用长度为-0.5的隔板还不足以充分调动湿地的有效容积，使短路和混合处于较低值，从而达到长宽比增至4倍的效果。由表9可得，随着长宽比增大，适宜隔长比也增大，而相同长宽比不同面积的湿地的适宜隔长比差异很小，几乎可以忽略。故可得适宜隔长比的大小与长宽比有关，与面积无关，且适宜隔长比随着湿地边界长宽比的增大而增大。

3 结 论

在试验场地限制无法增大长宽比的情况下，通过增加隔板长度也能达到类似的效果。本文将环境流体动力学模型（environmental fluid dynamics code，EFDC）模型用于表面流人工湿地水动力过程及水质过程的模拟，通过示踪试验及水质净化效果试验的数据对模型参数进行率定和验证，在此基础上探究了不同边界长宽比的表面流人工湿地的适宜隔长比，得到以下结论：

1）影响表面流人工湿地水力性能的敏感参数为背景值/常数的涡流黏度、无量纲水平扩散系数、边壁糙率和底部粗糙度；影响表面流人工湿地水质净化效果的敏感参数为最大硝化反应速率、硝化作用最适温度和底泥对磷酸根的吸收/释放通量。率定和验证的12组结果中，水动力模型模拟评价结果为中等及以上，即相关系数>0.7、纳什系数>0.4、相对误差<20%，的有7组，水质模型模拟评价结果为中等及以上有10组，即相对误差<20%，满足精度要求，故环境流体动力学模型可以用于表面流人工湿地水动力过程和水质过程的模拟。本文研究对象为层流，故模型参数背景值/常数的涡流黏度和无量纲水平扩散系数的取值相较于江河湖海等一般紊流水体要小。

2）在表面流人工湿地中，随着隔长比的增大，有效容积率、短路指标和矩指数增大，莫里尔离散指数减小，即湿地的水力性能随着隔长比的增大而提升。

3）在湿地表面积相同时，增加隔长比并不能明显提升净化效果指标总磷浓度去除率和总氮浓度去除率。

4）增大面积对表面流人工湿地的水力性能几乎没有影响，但却能显著提升湿地的净化效果。

5）适宜隔长比的大小随边界长宽比的增大而增大，且与表面流人工湿地的面积无关。从长宽比1、2、4的湿地变为长宽比4、8、16的湿地时，适宜隔长比分别为0.675、0.850和0.938，均比传统试验设计或工程应用中取值0.5、0.75、0.875偏大，这说明传统的设计方法还不足以充分调动湿地的有效容积，使短路和混合处于较低值，从而达到长宽比增至4倍的效果。

[1] 吴晓磊. 人工湿地废水处理机理[J]. 环境科学，1995(3)：83－86.

Wu Xiaolei. Mechanism of wastewater treatment in constructed wetlands[J]. Chinese Journal of Enviromental Science, 1995(3): 83－86. (in Chinese with English abstract)

[2] 万玉文，郭长强，茆智，等. 多级串联表面流人工湿地净化生活污水效果[J]. 农业工程学报，2016，32(3)：220－227.

Wan Yuwen, Guo Changqiang, Mao Zhi, et al. Sewage purification effect of multi-series surface flow constructed wetland[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(3): 220－227. (in Chinese with English abstract)

[3] Guo C, Cui Y, Dong B, et al. Test study of the optimal design for hydraulic performance and treatment performance of free water surface flow constructed wetland[J]. Bioresource Technology, 2017, 238: 461－471.

[4] 潘乐，茆智，董斌，等. 塘堰湿地减少农田面源污染的试验研究[J]. 农业工程学报，2012，28(4)：130－135.

Pan Le, Mao Zhi, Dong Bin, et al. Experimental research on reduction of agricultural non-point source pollution using pond wetland[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(4): 130－135. (in Chinese with English abstract)

[5] Ji Z G, Jin K R. An integrated environmental model for a surface flow constructed wetland: Water quality processes[J]. Ecological Engineering, 2016, 86: 247－261.

[6] Persson J, Somes N L G, Wong T H F. Hydraulics efficiency of constructed wetlands and ponds[J]. Water Science & Technology, 1999, 40(3): 291－300.

[7] Thackston E L, Shields F D, Schroeder P R. Residence time distributions of shallow basins[J]. Journal of Environmental Engineering, 1987, 113(6): 1319－32.

[8] Koskiaho J. Flow velocity retardation and sediment retention in two constructed wetland ponds[J]. Ecological Engineering, 2003, 19(5): 325－337.

[9] 朱永青. 人工湿地净化机制数学模型模拟及应用[D]. 上海：东华大学，2006.

Zhu Yongqing. Simulation and Application of Constructed Wetlands Pollutant Removal Mechanism Mathematical Model[D]. Shanghai: Donghua University, 2006. (in Chinese with English abstract)

[10] 蒲红杰，许士国，苏广宇. 滨库带多级表面流湿地水污染控制[J]. 东北水利水电，2016，34(9)：25－27.

Pu Hongjie, Xu Shiguo, Su Guangyu. Multi-level surface flow wetland water pollution control in Bin Kuta[J]. Water Resources & Hydropower of Northeast China,2016, 34(9): 25－27. (in Chinese with English abstract)

[11] Worman A, Kronnas V. Effect of pond shape and vegetation heterogeneity on flow and treatment performance of constructed wetlands[J]. Journal of Hydrology, 2005, 301(1/2/3/4): 0－138.

[12] German J, Jansons K, Svensson G, et al. Modelling of different measures for improving removal in a storm pond[J]. Water Science and Technology, 2005, 52: 105－112.

[13] Su T, Yang S, Shih S, et al. Optimal design for hydraulic efficiency performance of free-water-surface constructed wetlands[J]. Ecological Engineering, 2009, 35(8): 1200－1207.

[14] Cui L, Ouyang Y, Yang W, et al. Removal of nutrients from septic tank effluent with baffle subsurface-flow constructed wetlands[J]. Journal of Environmental Management, 2015, 153: 33－39.

[15] 马震，崔远来，郭长强，等. 基于水力性能和净化效果的表面流人工湿地设计参数优化[J]. 农业工程学报，2019，35(12)：157－164.

Ma Zhen, Cui Yuanlai, Guo Changqiang, et al. Optimization of design parameters of surface flow constructed wetland based on hydraulic performance and pollutant purification effect[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(12): 157－164. (in Chinese with English abstract)

[16] 季振刚. 水动力学和水质—河流、湖泊及河口数值模拟[M]. 北京：海洋出版社，2012.

[17] 江春波，张明武，杨晓蕾. 华北衡水湖湿地的水质评价[J]. 清华大学学报：自然科学版，2010，50(6)：848－851.

Jiang Chunbo, Zhang Mingwu, Yang Xiaolei. Water quality evaluation for the Hengshui Lake wetland in northern China[J]. Journal of Tsinghua University: Science and Technology, 2010, 50(6): 848－851. (in Chinese with English abstract)

[18] 赖秋英，李一平，张文一，等. 基于EFDC模型的湿地生物塘水质净化效果模拟与优化设计[J]. 四川环境，2017，36(1)：6－10.

Lai Qiuying, Li Yiping, Zhang Wenyi, et al. Study on the purification effect and optimization design of biological ponds in wetland based on EFDC Model[J]. Sichuan Environment, 2017, 36(1): 6－10. (in Chinese with English abstract)

[19] Meng X, Craig P M, Wallen C M, et al. Numerical simulation of salinity and dissolved oxygen at perdido bay and adjacent coastal ocean[J]. Journal of Coastal Research, 2011, 27(1): 73－86.

[20] 李一平，逄勇，丁玲. 太湖富营养化控制机理模拟[J]. 环境科学与技术，2004，27(3)：1－3.

Li Yiping, Pang Yong, Ding Ling. Ecological simulation of eutrophication for Taihu lake[J]. Environmental Science and Technology, 2004, 27(3): 1－3. (in Chinese with English abstract)

[21] 涂佳敏. 生态沟渠处理农田氮磷污水的实验与模拟研究[D]. 天津：天津大学，2014.

Tu Jiamin. Experiment and Simulation on Nitrogen and Phosphorus Removal of Ecological Ditch[D]. Tianjin: Tianjin University, 2014. (in Chinese with English abstract)

[22] 刘俊杰，董斌，郭长强，等. 人工湿地水力效率指标一致性与稳定性分析[J]. 灌溉排水学报，2014，33(Z1)：331－337.

Liu Junjie, Dong Bin, Guo Changqiang, et al.Analysis oil consistency and stability of hydraulic index in constructed wetland[J].Journal of Irrigation and Drainage, 2014, 33(Z1): 331－337. (in Chinese with English abstract)

[23] Wahl M D, Brown L C, Soboyejo A O, et al. Quantifying the hydraulic performance of treatment wetlands using the moment index[J]. Ecological Engineering, 2010, 36(12): 1691－1699.

[24] Guo C Q, Dong B, Liu J J, et al. The best indicator of hydraulic short-circuiting and mixing of constructed wetlands[J]. Water Practice and Technology, 2015, 10(3): 505－516.

[25] 程声通. 环境系统分析[M]. 北京：化学工业出版社，1990：18－20.

[26] Moriasi D N, Arnold J G, Liew M W V, et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J]. Transactions of the ASABE, 2007, 3(50): 885－900.

[27] Hamrick J M. A Three-dimensional Environmental Fluid Dynamics Computer Code: Theoretical and Computational Aspects[D]. Williamsburg: Virginia Institute of Marine Science, 1992.

[28] Wu G Z, Xu Z X. Prediction of algal blooming using EFDC model: Case study in the Daoxiang Lake[J]. Ecological Modelling, 2011, 222(6): 1245－1252.

[29] 郭元裕. 农田水利学[M]. 北京：中国水利水电出版社，2007：108－111.

[30] 雒文生，宋新元. 水环境分析及预测[M]. 武汉：武汉大学出版社，2000：28－30.

[31] Fathi-Moghadam M, Emamgholizadeh S. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows[J]. Journal of Hydraulic Research, 2009, 47(6): 691－699.

[32] Zhou J, Falconer R A, Lin B. Refinements to the EFDC model for predicting the hydro-environmental impacts of a barrage across the Severn Estuary[J]. Renewable Energy, 2014, 62(3): 490－505.

[33] 李一平，王静雨，滑磊. 基于EFDC模型的河道型水库藻类生长对流域污染负荷削减的响应：以广东长潭水库为例[J]. 湖泊科学，2015，27(5)：811－818.

Li Yiping, Wang Jingyu, Hua Lei.Response of algae growth to pollution reduction of drainage basin based on EFDC model or channel reservoirs: A case of channel reservoir, Guangdong Province[J].Journal of Lake Sciences, 2015, 27(5): 811－818. (in Chinese with English abstract)

[34] Li X, Zhang S L, Wang L X, et al. Coupling the EFDC and CE-QUAL-ICM models to simulate water quality of shallow lake in Inner Mongolia, China[C]// Sustainable Development: Proceedings of the 2015 International Conference on Sustainable Development (ICSD2015). 2015.

[35] Guo C, Cui Y, Dong B. Tracer study of the hydraulic performance of constructed wetlands planted with three different aquatic plant species [J]. Ecological Engineering, 2017, 102: 433－442.

[36] Jenkins G A, Greenway M. The hydraulic efficiency of fringing versus banded vegetation in constructed wetlands [J]. Ecological Engineering, 2005, 25(1): 61－72.

[37] Sabokrouhiyeh N, Bottacin-Busolin A, Nepf H, et al. Effects of vegetation density and wetland aspect ratio variation on hydraulic efficiency of wetlands[M]//Hydrodynamic & Mass Transport at Freshwater Aquatic Interfaces. Switzerland: Springer Nature, 2016: 101－113.

[38] Guo C Q, Cui Y L, Shi Y Z, et al. Improved test to determine design parameters for optimization of free surface flow constructed wetlands [J]. Bioresource Technology, 2019, 280: 199－212.

[39] Jong-Hwa H, Yoon C G, Won-Seok K, et al. The effect of physical design parameters on the constructed wetland performance[J]. Journal of the Korean Society of Agricultural Engineers, 2005, 47(5): 87－97.

Appropriate design for obstruction length-to-wetland length ratio in free-water-surface constructed wetlands based on environmental fluid dynamics code

Wan Di1, Cui Yuanlai1※, Guo Changqiang2, Ma Zhen1

(1.,,430072,; 2.,,310058,)

In practical engineering design, obstruction baffles are usually used in free-water-surface constructed wetlands (FWS CWs) to cut the width in half and double the length, thus the aspect ratio (length/width) increased fourfold. The length of the obstruction is often set to difference between boundary length and half the boundary width. In order to explore the design method’s reasonability and get an optimal value, the tests of FWS CWs under different aspect ratios are needed. In this study, we explored the influence of obstruction length-to-wetland length ratio (OL/WL) and aspect ratio on the hydraulic performance of FWS CWs. The environmental fluid dynamics code (EFDC) was used to establish the hydrodynamic model and water quality model of FWS CWs. Based on the tracer data and pollutant data of 12 FWS CWs, the calibration and verification of model parameters were carried out through sensitivity analysis and manual parameter adjustment. 2 kinds of wetlands named model wetlands and actual wetlands were established. 6 different areas and aspect ratios were set for the model wetlands, and the same as the actual wetlands. Each model wetland was provided with an obstruction, while the actual wetlands had no obstruction. The actual wetland corresponded to the model wetland one by one, that was, the aspect ratio of actual wetland was 4 times of the corresponding model wetland. The purpose of the simulation was to find an appropriate OL/WL that increased the aspect ratio of the model wetland to 4 times by comparing the hydraulic and treatment performance of the model wetlands and actual wetlands. The model wetland was simulated with multiple OL/WL to find the ratio that could make the model wetland and the actual wetland had the closest hydraulic and treatment performance. In addition, the hydraulic index,namelyeffective volume ratio, short circuit indicator, Morril dispersion index and moment index, were used to evaluate the similarity between the hydraulic performance of the 2 kinds wetlands. Similarly, the removal rates of total nitrogen and total phosphorous were used to evaluate the treatment performance’s similarity. The results showed that: 1) The sensitive parameters affecting the hydraulic performance were background horizontal eddy viscosity, dimensionless horizontal momentum diffusion, wall roughness and bottom roughness, and those affecting the treatment performance were maximum nitrification rate, reference temperature for nitrification and constant benthic flux rate of phosphorous. Among the 12 groups, 7 groups were satisfactory or better in hydrodynamic model with correlation coefficient higher than 0.7, Nash-Suttcliffe higher than 0.4, and relative error smaller than 20%; and 10 groups were satisfactory or better in water quality model. The calibrated and verified EFDC model could be used to simulate the hydrodynamic process and purification process of FWS CWs. 2) The 4 hydraulic index had good consistencies. As the increase of OL/WL, effective volume ratio, short circuit indicator and moment index increased and Morril dispersion index decreased. The larger the effective volume ratio, short circuit indicator and moment index would lead to smaller morril dispersion index and better hydraulic performance, which indicated the hydraulic performance increased with the increase of OL/WL. 3) The removal rate of total nitrogen and the phosphorous didn’t change greatly as the OL/WL increased. 4) Changing the area had great impact on the treatment performance. 5) When the aspect ratio ranged from 1, 2, 4 to 4, 8, 16, the appropriate OL/WL was 0.675, 0.850, 0.938, which was different from the values of 0.5, 0.75, 0.875 in the traditional test design or engineering application.

hydraulic performance; treatment effects; optimization; free-water-surface constructed wetlands; obstruction length-to-wetland length ratio; aspect ratio; EFDC model

万 荻，崔远来，郭长强，马 震. 环境流体动力学模拟优选人工湿地设计中隔板湿地长度比[J]. 农业工程学报，2019，35(18)：62－69.doi：10.11975/j.issn.1002-6819.2019.18.008 http://www.tcsae.org

Wan Di, Cui Yuanlai, Guo Changqiang, Ma Zhen. Appropriate design for obstruction length-to-wetland length ratio in free-water-surface constructed wetlands based on environmental fluid dynamics code[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(18): 62－69. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.18.008 http://www.tcsae.org

2019-03-27

2019-08-10

国家自然科学基金项目（51779181）；江西省水利科技项目（KT201737）

万 荻，主要从事农田水环境修复技术模拟研究。Email：DiWan1995@whu.edu.cn

崔远来，教授，博士，主要从事节水灌溉和农业面源污染治理研究。Email：YLCui@whu.edu.cn

10.11975/j.issn.1002-6819.2019.18.008

S156.8

A

1002-6819(2019)-18-0062-08