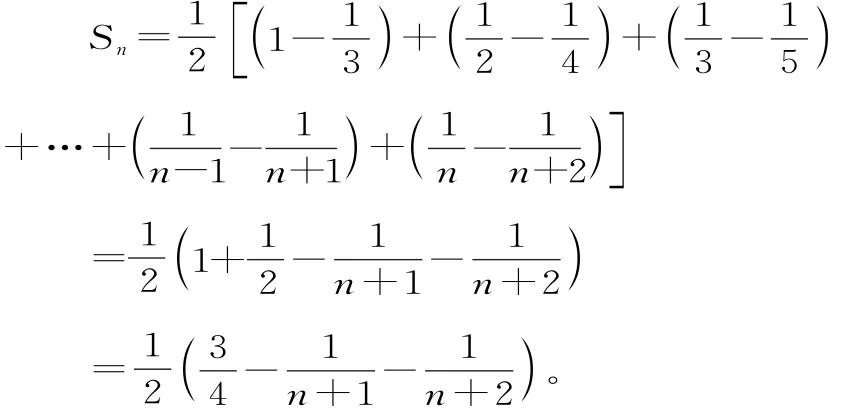归纳数列中常见的易错题型

■河南省平舆县第一高级中学 李合举

一、数列概念理解不透，由Sn求an时忽略n=1的情况

对于数列an与Sn之间有如下关系：an利用两者之间的关系可以已知Sn求an。但注意只有在当a1适合an=Sn-Sn-1(n≥2)时两者才可以合并，否则要写成分段函数的形式。

例1已知数列{an}的前n项之和Sn=a qn(a≠0，q≠1，q为非零常数)，则{an}为( )。

A.等差数列

B.等比数列

C.既不是等差数列，也不是等比数列

D.既是等差数列，又是等比数列

错解：因为an+1=Sn+1-Sn=a qn+1-a qn=a qn(q-1)，所以an=Sn-Sn-1=a qn-1(q-1)，所以(常数)，所以{a}为等比n数列。故选B。

错因分析：错解中忽略了an=Sn-Sn-1时的隐含条件n＞1。

正解：当n=1时，a1=S1=a q；当n≥2时，所以q(常数)，但因为，所以{an}既不是等差数列，也不是等比数列。故选C。

同类题型：已知数列{an}的前n项之和为Sn=n2+n+1，则数列{an}的通项公式为

解析：当n=1时，a1=S1=3；

当n≥2时，an=n2+n+1-(n-1)2-(n-1)-1=2n。

二、忽视对等比数列中公比的分类讨论

等比数列求和公式应用时要对q=1，q≠1讨论。

例2设等比数列{an}的前n项和为Sn。若S3+S6=2S9，求数列{an}的公比q。

错解：因 为S3+S6=2S9，所 以，整理得q3(2q6-q3-1)=0。

由q≠0得方程2q6-q3-1=0，所以，所以或q=1。

错因分析：在错解中，由，整理得q3(2q6-q3-1)=0时，应有a1≠0和q≠1。在等比数列中，a1≠0是显然的，但公比q完全可能为1，因此，在解题时应先讨论公比q=1的情况，再在q≠1的情况下，对式子进行整理变形。

正解：若q=1，则有S3=3a1，S6=6a1，S9=9a1。但a1≠0，即得S3+S6≠2S9，与题设矛盾，故q≠1。

同类题型：在数列{an}中，a1=1，a2=2，数列{anan+1}是公比为q(q＞0)的等比数列，则数列{an}的前2n项和

解析：因为数列{anan+1}是公比为q(q＞0)的等比数列，所以，即这表明数列{an}的所有奇数项成等比数列，所有偶数项成等比数列，且公比都是q。

又a1=1，a2=2，当q≠1时，S2n=a1+

当q=1时，S2n=a1+a2+a3+a4+…

三、利用函数知识求解数列相关问题时易忽略其定义域是正整数集或其子集

例3等差数列{an}的首项a1＞0，前n项和为Sn，当l≠m时，Sm=Sl。问：当n为何值时Sn最大?

易错点分析：等差数列的前n项和是关于n的二次函数，可将问题转化为求解关于n的二次函数的最大值，但易忘记此二次函数的定义域为正整数集这个限制条件。

解析：由题意知Sn=f(n)=n a1+，此函数是以n为变量的二次函数。因为a1＞0，当l≠m时，Sm=Sl，故d＜0，即此二次函数开口向下。由f(l)=f(m)知，当时，f(x)取得最大值，但由于n∈N*，故若l+m为偶数，当时，S最大。若ln+m为奇数，当时，Sn最大。

同类题型：设等差数列{an}的前n项和为Sn，已知a3=12，S12＞0，S13＜0。

(1)求公差d的取值范围；

(2)指出S1，S2，…，S12中哪一个值最大，并说明理由。

易错点分析：(1)依据S12＞0，S13＜0，直接列方程求解d的范围即可；(2)判断出转折项即可找出前n项和的最大值。无论应用二次函数求最值，还是利用找转折项求最值，两种方法都具有一般性，但需要注意的是，利用二次函数求最值时，要注意n只能取正整数，找转折项可以利用通项公式解不等式，但是计算比较烦琐，这时可以合理选择应用数列的性质，以简化运算和判断。

解析：(1)依题意，有S12=12a1+

由a3=12，得a1=12-2d。 ③

(2)由d＜0可知a1＞a2＞a3＞…＞a12＞a13，因此，若在1≤n≤12中存在自然数n，使得an＞0，an+1＜0，则Sn就是S1，S2，…，S12中的最大值。由于S12=6(a6+a7)＞0，S13=13a7＜0，即a6+a7＞0，a7＜0，由此得a6＞-a7＞0。因为a6＞0，a7＜0，故在S1，S2，…，S12中，S6的值最大。

四、使用累加、累乘及相消法求和时，要正确辨别剩余项，以免出错

例4求的值。

易错点分析：本题解答时，若不从通项入手分析各项的特点就很难找到解题突破口，其次，在裂项抵消中间项的过程中，对消去哪些项剩余哪些项的规律不清而导致解题失误。“裂项法”有两个特点，一是每个分式的分子相同；二是每项的分母都是两个(也可三个或更多)数相乘，且这两个数的第一个数是前一项的第二个数，如果不具备这些特点，就要进行转化。同时要明确消项的规律：一般情况下，剩余项是前后对称的

解析：由等差数列的前n项和公式得所以n取 1，2，3，…，就 分 别 得 到

同类题型：求的值。

解析：令