基于安全车速差的高速公路特长隧道环境驾驶人行为风险特性研究

吴 玲， 胡 昊， 赵炜华， 朱 彤， 刘浩学

(1. 西安航空学院车辆工程学院， 陕西 西安 710077; 2. 长安大学 汽车运输安全保障技术交通行业重点实验室， 陕西 西安 710064)

0 引言

随着隧道建设占高速公路基础建设的比重越来越大，与之相伴的交通安全问题也日益突出。事故数据表明，隧道进、出口段交通事故分布最多，总数占比近70%，且追尾事故占比近55%[1]，事故严重程度高于开放道路段[2]； 而影响交通安全的诸多因素中，驾驶人因素占事故总数的93%左右[3]。由于隧道空间结构特殊、内部与外部的环境条件存在巨大的差距，驾驶人在行车过程中需要经受若干次的明暗光线变化，生理、心理都将受到一定影响，进而对驾驶行为造成干扰，甚至出现车辆失控现象。人、车、路、环境共同构成了完整的反馈系统，在这个系统中，道路安全很大程度上取决于驾驶人的行为风险。行为风险值减小，会使事故可能性显著下降，道路安全性得到明显改善。因此，如何寻求合适的驾驶绩效指标，表征驾驶人行为风险，以此衡量和判断隧道驾驶过程中的行为风险变化关键位置点值得深入研究。

国际上对这一问题通常采取模拟器试验的形式进行研究，分析隧道和普通高速2种不同路段中驾驶人的绩效指标并加以对比[4-6]； 国内关于隧道路段交通安全的研究大多反映在事故数据的收集和分析[7-8]、驾驶人的身心变化特点[9-10]、车速与安全的关系评价[11-13]、出口段车速改变规律[14]等内容。杜志刚等[10]进行实车试验，借助眼动仪等设备分析了出口段驾驶人瞳孔面积和车速之间的联系，得到了临界安全车速； 景天然[15]、梁夏等[16]基于调查的交通事故数据，采用统计分析方法，提出了道路交通安全评价方法及交通事故率的综合影响系数； 叶亚丽等[17]借助人工智能中的云模型方法，构建了基于生理特征的公路安全评价方法； 闫彬等[18]通过实地测试，分析了驾驶人感知特性对隧道群交通安全的影响。

综上所述，现有的研究很少从安全机制层面出发展开安全评价，未能形成一种兼顾主观认知与客观环境2类因素的综合研究模型，尤其是缺少对隧道空间中驾驶人行为风险变化特性的关注。速度可以作为驾驶行为的重要表征，能够在很大程度上体现驾驶预期以及行车环境条件，是定量描述驾驶风险性高低的关键指标[19]。基于此，本文选取2座有代表性的特长隧道开展实车自然驾驶试验，收集相关速度数据，提出基于安全车速差的驾驶人行为风险量化方法，分析对比熟练驾驶人与非熟练驾驶人的行为风险变化特性及差异性，以期为道路安全预警、安全设施优化提供参考。

1 特长隧道环境实车试验

1.1 试验路段

本文选取的用于实车试验的特长隧道属于蓝商高速。蓝商高速在建设过程中严格遵循双向4车道的设计标准，共包含226座桥梁和35座隧道，单洞长度累计37.13 km。其中，李家河3#隧道、秦岭隧道属于特长隧道，分别长4 259 m和4 748 m，2条隧道都采取了双洞单向的形式，均为2条双车道，最高行车速度为60 km/h，与普通高速路段(简称普通路段)相比低了20 km/h。由于途径秦岭地区，蓝商高速拥有众多隧道，能够比较客观地反映环境改变对驾驶行为的影响。对该路段进行实地考察，结果显示该路段处于自由流状态，驾驶人结合自身的习惯、车辆情况以及道路情况等对车速进行灵活控制，受路况的影响较小。

1.2 试验人员选择

由于所选的试验路段比较特殊，为了保证试验人员的人身安全以及数据的准确可靠，要求试验人员的实际驾驶经历超过3年、身体健康、视觉技能达标、无不良驾驶记录，并拥有充分的隧道驾驶经验。根据以上要求，共选取30名合格者，包含15名专职的驾驶人(隧道从业人员)以及15名非专职人员。其中，前者对试验路段的情况比较熟悉，属于熟练驾驶人，年龄均值约35.7岁，驾龄均值超过14年；后者对试验路段的情况比较陌生，年龄均值约39.2岁，驾龄均值约13.6年。本文驾驶经验变量指该试验人员是否常驾驶试验路段，据此分析对路段的熟悉程度是否会对安全驾驶造成影响。驾驶人信息见表1。

表1 驾驶人信息(均值±标准差)

1.3 试验设备

试验中所有驾驶人所用车辆均为2007款起亚新佳乐，全部安装行车记录仪，试验时实载4人，车辆技术状况良好。车速采集有2种形式，一种是利用安装在固定地点的NC200地磁感应装置，一种是利用GPS定位或雷达实现车速信息的收集。前者在采集范围上存在较大的局限性，只能实现定点采集；后者应用比较灵活，但是无法在特长隧道内使用，并且数据存储比较困难。为了获得实时行车速度，通过OBD车载自动诊断系统接口对数据进行采集，利用蓝牙将采集的数据传输到芯片中保存，等待后续的统计和处理。OBD安装位置如图1所示。

1.4 试验过程

试验前，将试验路线提供给试验人员，要求其根据自身习惯驾驶2007款起亚新佳乐通过隧道。行车前对行车记录仪以及车速信息存储芯片的信息进行同步处理，通过隧道后再次进行同步。对收集到的信息进行分析之前，需要利用交叉验证的形式确定车辆进入和离开隧道的时间，对路段进行划分，然后对数据进行处理。试验过程现场照片如图2所示。

图1 OBD安装位置

图2 试验过程

1.5 数据预处理

1.5.1 路段划分

根据JTG D70/2—2014《公路隧道设计规范》的要求，隧道照明段的长度和亮度都必须满足一定的标准，并且应结合照明停车视距等因素确定出入口段、过渡段等不同道路环境下的照明长度。基于隧道照明段长度、亮度相关规定，依据照明停车视距、隧道内净空高度、设计速度、交通量等提出了入口段、过渡段、中间段、出口段照明长度。此外，针对道路线形，JTG D20—2017《公路路线设计规范》要求隧道洞口内外的线形应保持协调，具体标准为： 隧道洞口内外侧各3 s设计速度行程长度范围的平、纵面线形应一致。按普通山区高速公路80 km/h的车速，3 s的行程长度约为67 m。

结合以上规范要求，将试验路段范围拓展到洞口外部300 m的位置，并将试验路段划分为入口、行车、出口3段。其中，入口段长度为600 m，隧道入口前后各300 m； 出口段长度为600 m，隧道出口前后各300 m； 隧道内其他路段均属于行车段。

为了保证研究结果的准确性和普适性，消除道路线形等其他因素的干扰，本文不仅选择了具有代表性的隧道，即2座特长隧道必须是山区高速公路特长隧道，且所在高速公路涵盖隧道路段较多； 而且在数据处理方面也采取了相应的措施： 入口、行车、出口等路段均包含上下行2个方向，可以由此分析特长隧道条件下驾驶人的行为风险特征，避免了单一方向的特殊性。路段划分及行车区间划分如图3所示。

图3 路段划分及行车区间划分示意图

1.5.2 行车区间切分

以往关于隧道环境对驾驶人眼动行为或生理指标影响的研究，一般是从出口段或入口段某个地点对单一指标信息进行横向对比，并没有分析数据是否准确、是否存在异常。本文在3段划分的基础上，对行车区间进行细分，按照50 m的间隔将出入口段分别切割为12个小区间； 行车段则等距离选取20个点，细分为19个小区间，最终将整个隧道划分为43个行车区间。原先以某一位置点为指标难以表征此处驾驶人行为状态，而区间平均指标包含的数据量更多，体现的信息更加丰富，可以更好地反映变化特征。最终得到的数据是上下行2个方向对应指标的平均值。

2 行为风险评价指标的确定方法

2.1 主观预期车速

主观预期车速是驾驶人根据其所在的行车环境估计得到的行车速度，即驾驶人在心理上自认为安全的车速状态，而非道路交通环境允许的安全速度。行车环境改变，主观预期车速也将随之出现变化，并据此对实际车速进行调整，不断重复这一过程。速度作为驾驶行为特性的核心表征，是外部行车环境对驾驶人影响的体现。隧道出入口光环境的骤变及内部行车环境的封闭性，都决定了实际车速的变化存在一定的滞后，这种滞后的存在将造成主观预期车速和所在环境对应的安全车速之间出现偏差，这是酿成交通事故的重要诱因。

2.2 客观安全车速

综合行车环境包含道路情况、车流情况、安全设施等多种因素。结合自身能力(车道保持能力、换道能力、对突发事件的应激处理能力等)，驾驶人根据综合行车环境能够保持安全行驶的最大车速，称为“客观安全车速”。该速度由行车环境决定，是其反馈给车辆的安全允许速度。客观安全车速的数值将随行车环境的改变而不断改变。

2.3 驾驶人行为风险评价指标

结合以上2类速度，可以体现驾驶人对所在行车环境的主观判断与外部环境的要求。因此，可认为驾驶人行为风险源于两者偏差，这种偏差可以通过2种车速进行计算。在具体的行车过程中，主观车速和客观车速之间存在以下几种情况：

1)两者基本一致。驾驶人主观层面上对行车环境的判断与实际比较接近，在实际环境允许的安全范围内行驶。这种情况下驾驶人的行为风险值较低，不容易发生交通事故。

2)预期车速低于安全车速。驾驶人主观层面上对行车环境的判断存在偏差，认知得到的危险程度超过实际程度。该情况下，虽然当前行为风险值低，但驾驶人负荷过高，其行为风险值在后续的行车过程中可能大幅度增加。

3)预期车速超过安全车速。驾驶人主观层面上的判断出现错误，预期车速高于实际环境所能允许的安全值。这种情况下行为风险值较高，容易引发交通事故。

对驾驶人的行为风险进行定量研究，最终目的是判断关键位置点，确定事故隐患路段，据此对安全设施加以优化，确保交通安全。构建风险评价模型的难点，集中在如何对2种车速进行量化方面。本文以实测车速作为预期车速，即驾驶人在各个小区间的实测行驶速度，既有隧道路段的数据，也有普通路段的数据。

在客观安全车速方面，本文主要参考了文献与统计数据。Solomon提出事故发生的概率和车速之间的关系曲线为U形，在平均车速附近发生交通事故的概率最低；运行车速与平均车速之间的差值越大，出现交通事故的概率越高[20]。根据交通工程学，一般以85%定点单车自由流分位车速作为最高限制车速。对于本文所选择的特长隧道路段，道路限速最高为60 km/h，对于最低速度未作明确要求；对于普通路段，道路限速最高为80 km/h，最低为60 km/h。对基础数据进行统计，全部试验人员85%分位车速都超过了限速范围。若所有试验人员均采用单一最高限速值作为安全车速值，由于熟练和非熟练驾驶人对2条隧道的熟悉情况存在差距，很容易造成前者的行为风险值出现高估的情况。考虑到以上内容，对比不同路段车速分布情况，选择中位数分割的方式[21]，最后决定采用50%分位车速作为试验人员在2条试验路段的安全基准值；结合各路段的限速数据，通过比例指标，得到安全车速的上下限；按照U形曲线，选择二者的均值作为客观安全车速。以上方法符合法律规定，并且比较充分地照顾了不同试验人员的个体差异以及路段环境特点。试验实质是在以下假设的基础上进行的。

1)特长隧道环境入口、出口、行车等不同路段以及普通路段对应不同的客观安全车速。

2)由于熟练驾驶人对于路况比较了解，所以其安全车速相对较高。

3)主观车速和客观车速之前的偏差越大，其行为风险值越高。

最高安全车速确定方法如下： 全部试验人员在隧道的出口或入口都将经历光线的敏感变化，速度将出现较大改变； 而隧道内部光线比较一致，速度相对稳定，并且车速较高，所以非熟练驾驶人在隧道路段以60 km/h作为安全车速上限，普通路段则以80 km/h作为安全车速上限。统计确定熟练和非熟练驾驶人在不同路段的50%分位车速，然后通过比例指标计算其他路段的安全车速最高值。具体采取以下方法计算。

隧道路段(入口段、行车段、出口段)：

(1)

式中：vihs为i路段最高安全车速；vi50为i路段50%分位车速； 60 km/h为非熟练驾驶人行车段最高安全车速； 70.41 km/h为非熟练驾驶人行车段50%分位车速。

普通高速路段：

(2)

式中：vphs为普通路段最高安全车速；vp50为普通路段50%分位车速； 80 km/h为非熟练驾驶人普通路段最高安全车速； 94.51 km/h为非熟练驾驶人普通路段50%分位车速。

计算后确定的最高安全车速信息见表2。观察表2中数据可知，入口段的速度最低，普通路段的速度最高。

表2 最高安全车速

最低安全车速确定方法如下： 隧道不设最低车速，普通路段车速不能低于60 km/h，所以，针对非熟练驾驶人，在普通路段的最低安全车速设为60 km/h，其他路段则通过比例指标确定。计算方法如下：

(3)

式中：vils为i路段最低安全车速；vi50为i路段50%分位车速。

计算后确定的最低安全车速信息见表3。根据表3中数据可知，入口段的速度最低，普通路段的速度最高。

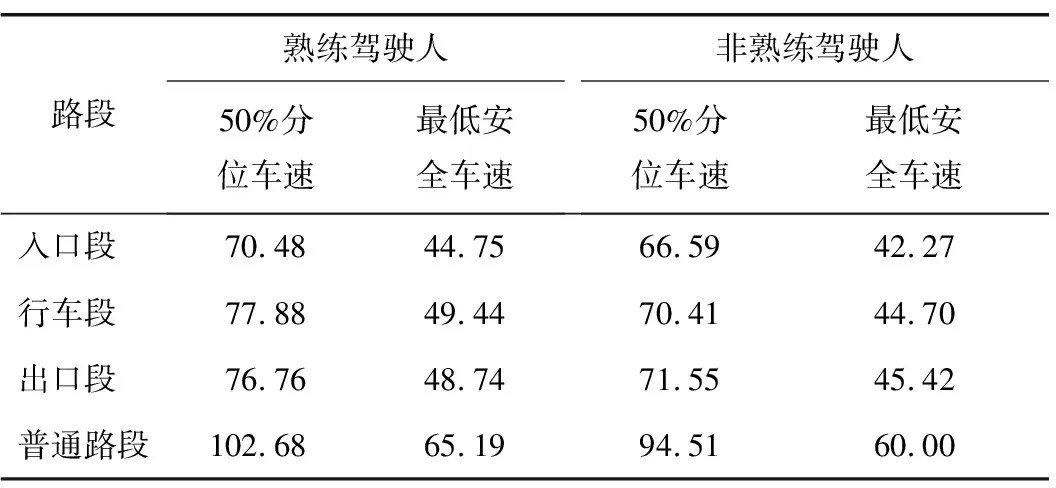
表3 最低安全车速

结合U形曲线，将最高与最低安全车速的平均值作为客观安全车速，结果见表4。由表4中数据可知，入口段的速度最低，普通路段的速度最高。

表4 最终安全车速值

3驾驶人行为风险量化结果

采用主观预期车速与客观安全车速差值的绝对值作为驾驶人行为风险的量化指标，简称安全车速差。安全车速差值越大，说明驾驶人行为越不安全，其行为风险值越高。确定各个区间的差值后，由于缺少参考量纲，所以不能进行横向对比。为此，通过极值处理法对所得数据进行变换，消除量纲的影响，全部转换到0～1内，据此确定行为风险值。具体转换方式如下。

所有样本表示为：

(4)

极差表示为：

(5)

式中xij为i区间j位试验人员的安全车速差，km/h。

极差标准化转换结果表示为：

(6)

式中：i=1，2，…，n；j=1，2，…，m。

经过标准化处理后，数据最低为0，最高为1，无量纲。

3.1 入口段驾驶人行为风险变化规律

每隔20 m，采用保形分段3次Hermite插值法确定入口段2种类型的试验人员在不同位置处的行为风险值，具体见图4和图5。图中负值表示隧道外，正值表示隧道内。

图4 熟练驾驶人入口段各位置点行为风险变化曲线

由图4可知，对于熟练驾驶人，在隧道外距离入口大于100 m范围内受道路环境的影响较小，行为风险值仅有0.31； 在隧道外距离入口100—20 m所受影响逐渐增大，行为风险值出现上升，增长幅度约为17.97%；在隧道内外距离入口20 m范围内，所受影响比较一致，行为风险值稳定在0.37附近；隧道内影响逐渐变大，行为风险值不断增加。行为风险值对应的曲线可以在一定程度上反映车速的改变，即熟练驾驶人在入口段的行车速度变化规律为： 变快—稳定—变快。因此，对比2种类型驾驶人行为风险变化可知，相对于非熟练驾驶人，当试验人员对路况比较熟悉时，不会将入口段作为事故高发路段，不会提前减速以减少隐患，甚至出现了加速的情况，其行为风险值相对较高，并且在隧道内外距离入口20 m范围内微弱增加。

图5 非熟练驾驶人入口段各位置点行为风险变化曲线

对于非熟练驾驶人，在隧道外距离入口300 m范围内风险值逐渐降低，这一趋势一直保持到隧道外距离入口80 m处，减少幅度达到14.89%； 在隧道外距离入口80 m到隧道内距离入口120 m范围，行为风险值比较稳定，保持在0.33附近；进入隧道，行为风险值继续下降，这一趋势维持到隧道内距离入口220 m处，减少幅度约为9.29%。因此，非熟练驾驶人在入口处的行为风险表现出以下规律： 减少—稳定—减少。当试验人员适应隧道环境后，行车速度将增加，行为风险值变高。非熟练驾驶人对道路情况缺乏了解，在进入隧道前将先行减速，心理上处于紧张状态，并且在隧道内外距离入口20 m范围内，行为风险值出现微小的下降。

3.2 出口段驾驶人行为风险变化规律

出口段熟练驾驶人与非熟练驾驶人各位置点行为风险变化曲线如图6和图7所示，图中负值表示隧道内，正值表示隧道外。由图可知，车辆驶近隧道出口并离开的过程中，熟练驾驶人的车速减慢，行为风险值出现微小的下滑，幅度约为5.78%； 隧道外距离出口大于20 m范围，行为风险值大幅度降低。本文所选择的熟练驾驶人都是与隧道接触较多的人员，从光线昏暗的隧道进入光线明亮的环境，根据常理推断其行车速度将出现一定的上升，即行为风险值变高，但是试验数据则恰恰相反，可能是由于这一部分试验人员认为出口处可能存在隐藏的车速测量装置。

图6 熟练驾驶人出口段各位置点行为风险变化曲线

隧道内距离出口大于120 m范围的环境对于非熟练驾驶人而言影响较小，其行为风险值约0.41； 隧道内距离出口120～20 m试验人员的行为风险值出现了明显的降低，减少幅度约6.42%；之后其行为风险值快速降为0.33，减少幅度达到11.63%；当试验人员了解环境后，行车速度加快，行为风险值重新变大。因此，非熟练驾驶人在出口段的行为风险表现出以下规律： 降低—突然下降—升高，并且在隧道内外距离出口20 m范围内出现了微小的下降。

3.3 特长隧道路段与普通路段行为风险变化曲线

按照本文的计算方法，可得到所有试验人员行驶通过整个特长隧道的行为风险值。由于所得数据为各个小区间的车速，因此最后获得的行为风险值也对应不同的区间。图8示出1号试验人员(熟练驾驶人)在各个区间的行为风险情况。由图8可知，沿着车辆行驶方向，1号试验人员的行为风险值表现出增高—稳定—降低的规律。

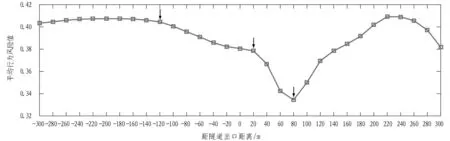
图7 非熟练驾驶人出口段各位置点行为风险变化曲线

图8 1号试验人员整段隧道行为风险变化曲线

2种类型试验人员的行为风险变化曲线如图9和图10所示，其中入口段前半段、出口段后半段在隧道外，其余在隧道内。由图9可知，入口前半段，熟练驾驶人的行为风险值低于非熟练驾驶人，入口后半段则恰恰相反； 行车段前半段，熟练驾驶人的行为风险值超过非熟练驾驶人，后半段则低于非熟练驾驶人； 出口前半段，熟练驾驶人表现出更高的行为风险值，出口后半段则相对偏低。由图10可知，在普通路段前半段，非熟练驾驶人的风险值相对较高；后半段则相对较低。本文中所选取的普通路段为驾驶人即将进入隧道的高速路段，在前半段，因熟练驾驶人对道路环境较为熟悉，因此其行为风险值相对较低；而在后半段快进入隧道时，非熟练驾驶人认为隧道行车风险较高，因此降低了车速，其行为风险值相对减小。

图9 2种类型驾驶人整段隧道平均行为风险变化曲线

图10 2种类型驾驶人普通高速路段平均行为风险变化曲线

图11示出所有试验人员在隧道路段和普通高速路段的平均行为风险值。由图11可知，熟练驾驶人在出入口段的行为风险值与行车段相比偏低；非熟练驾驶人则在出口段表现出较高的行为风险值； 2种试验人员在普通路段的行为风险值明显高于隧道路段，并且在入口段都表现出较低的风险值。

图11 不同路段行为风险

3.4 车速与行为风险关系

对于隧道路段和普通路段，分别绘制不同类型试验人员行车速度和行为风险之间的散点密度图如图12所示，并对其进行皮尔逊相关分析。由于行为风险值的计算是以测量得到的车速信息为基础，所以二者之间为正线性相关(r=0.906； Sig.=0.000)。由图12(a)可知，隧道路段熟练驾驶人的行车速度分布在75～85 km/h，行为风险值分布在0.4～0.5； 由图12(b)可知，非熟练驾驶人的行车速度分布在65～80 km/h，行为风险值分布在0.3～0.5。在普通路段，熟练驾驶人的行车速度分布在100～110 km/h，行为风险值分布在0.5～0.6(见图12(c))； 非熟练驾驶人的行车速度分布在90～110 km/h，行为风险值分布在0.4～0.6(见图12(d))。此外，与熟练驾驶人相比，非熟练驾驶人的热点分布区域相对较广，表明不同试验人员之间存在较大的差距。

(a) 熟练驾驶人特长隧道路段

(b) 非熟练驾驶人特长隧道路段

(c) 熟练驾驶人普通高速路段

(d) 非熟练驾驶人普通高速路段

熟练驾驶人由于对试验路段比较了解，因此行车速度明显偏高。按照行为风险量化模型的分析结果，其风险均值也明显偏高。可见，试验人员熟悉路况不会导致行为风险值降低，甚至反而造成风险值增加。

4 安全车速差特性分析

分别对每个路段计算其实测速度与安全速度之间差值的绝对值，确定不同类型试验人员的情况，并据此绘制安全车速差箱线图如图13和图14所示。由图13和图14可知，熟练驾驶人的车速差统计量相对较大，其中行车段的车速差均值明显高于出入口段； 对于非熟练驾驶人，则出口段的车速差均值最大。此外，不管是那种类型的试验人员，在普通路段的车速差均超过隧道路段。从不同路段的视角出发，普通路段的车速差统计量显著超出隧道路段；入口段的车速差均值最低，行车段与出口段的车速差均值比较接近。

图15示出2种不同类型试验人员的安全车速差分布比例情况。由图15可知，不同曲线比较类似但是存在一定差异，熟练驾驶人在入口段和行车段的车速差占比最大的是10～20 km/h，出口段和普通段则是20～30 km/h；对于非熟练驾驶人，入口、行车、出口等路段的车速差占比最大的是10～20 km/h，普通路段则是20～30 km/h。所以，隧道路段的车速差相对较小，普通路段较大。

图13 不同类型驾驶人安全车速差箱线图

Fig. 13 Box plot of safe speed difference for different types of drivers

(a) 各路段折线图

(b) 各路段箱线图

(a) 熟练驾驶人

(b) 非熟练驾驶人

5 结论与讨论

本文选择有代表性的高速公路特长隧道作为试验路段，测量熟练和非熟练2种类型试验人员的速度数据，基于文献总结与数据统计，通过中位数分割的方法，结合路段实际限速值，提出基于主观预期车速与客观安全车速差值绝对值的驾驶人行为风险量化方法。得到区间行为风险值后，采用保形分段3次Hermite插值法，比较不同类型试验人员在入口、行车、出口等不同路段以及普通高速路段的行为风险变化情况，以及2种路段环境下的风险值差异。此外，还分析了特长隧道环境与普通路段的安全车速差规律。主要结论如下：

1)进入隧道前，入口外部熟练驾驶人的行为风险值低于非熟练驾驶人；入口内部则恰恰相反。行车段前半段，熟练驾驶人的行为风险值超过非熟练驾驶人，后半段则低于后者。出口内侧熟练驾驶人表现出更高的行为风险值，出口外侧则相对偏低。即在隧道内部，熟练驾驶人行为风险值高于非熟练驾驶人；而在隧道外部，非熟练驾驶人行为风险更高一些。

2)在隧道路段，熟练驾驶人在出入口段的行为风险值与行车段相比偏低；非熟练驾驶人则在出口段表现出较高的行为风险值； 2种试验人员在普通路段的行为风险值明显高于隧道路段，并且在入口段都表现出较低的风险值。

3)在隧道路段，熟练驾驶人的行车速度分布在75～85 km/h，行为风险值分布在0.4～0.5； 非熟练驾驶人的行车速度分布在65～80 km/h，行为风险值分布在0.3～0.5。在普通路段，熟练驾驶人的行车速度分布在100～110 km/h，行为风险值分布在0.5～0.6； 非熟练驾驶人的行车速度分布在90～110 km/h，行为风险值分布在0.4～0.6。

4)对于不同类型的试验人员，隧道路段安全车速差占比最大的均为10～20 km/h，而普通路段则为20～30 km/h。

所有试验人员均在入口段行为风险值最低，在普通路段行为风险值最高，这也说明所有试验人员认为隧道入口段风险系数较高，所以会保持较低的安全车速差，即在隧道入口段需注意相关标志、标线以及安全设施的布置以降低其风险系数。对于熟悉道路条件的熟练驾驶人，因其安全车速差较非熟练驾驶人更高，且在多发事故路段(入口段)并未出现行为风险值降低的趋势，这在一定程度上增加了事故隐患，需在实际安全设施布置过程中，考虑其行为风险值突变点布置合理的安全保障措施，即在入口段驾驶人行为风险值骤增的区域(隧道外距入口100 m到隧道内距入口220 m范围)考虑布置安全保障设施。受各方面条件的约束，本文仅基于安全车速差建立了行为风险评价模型，下一步建议多加入一些纵向驾驶绩效指标和横向绩效指标，如跟车距离、车头视距、TTC、横向偏移距离、横向速度等。