Ivancevic 期权模型的新的周期波解

五原县第一中学,内蒙古自治区巴彦淖尔市 015100

引言

根据现代市场运行规律，Ivancevic 在文献[1]，[2]中提出了一个新的适应性非线性薛定谔方程，也称为Ivancevic 期权模型(the Ivancvic option price model)：

其中i为虚数单位，s为股票价格，t为时间变量，φ(s，t)为期权波函数，σ，β均为由市场自身决定的常数.在物理学领域，方程(1)是(1+1)维非线性薛定谔方程，在很多物理领域都有重要应用.

1 Ivancevic 期权模型的行波约化

如果β=0，则方程(1)退化为线性薛定谔方程.在这里我们考虑β≠0的情形.对于方程(1)，

方程（1）化为如下的二阶三次非线性自治常微分方程

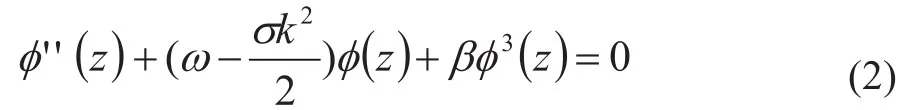
在文献1中，Ivancevic 得到了如下的雅克比椭圆函数解：

当0≤m＜1

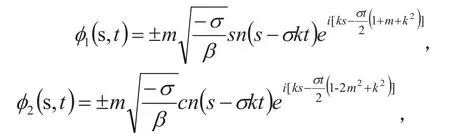
m=1：

其中，sn，cn为雅克比椭圆函数，m为雅克比椭圆模.解φ1，φ2为通解,解φ3为暗孤子解，φ4为亮孤子解 [1]。这些解应该在某种程度上可以解释期权波函数φ(s，t)的变化规律。

本文将在文献1的基础上，利用复方法，通过求解获得方程(1)的新周期波解.

2 利用复方法求方程(1)的周期波解

复方法是 Yuan 等 [4]提出的一种新型的求自治非线性复常微分方程的方法，具有简便高效系统的特点，下面我们利用该方法求解方程(2)的周期波解.

为了应用该方法，我们先给出如下概念和引理.记函数集合W={椭圆函数，有理函数，的有理函数}。

考虑如下的常微分方程

其中n∈N,b≠0,c是常数．

假设亚纯函数w为方程(3)的具有极点的解．如果把洛朗级数代入方程(3)，通过平衡各同类项系数，能依次确定p组系数即能确定如下的p个洛朗级数主要部分那么

我们称方程(3)满足弱 ＜p，q＞条件.

引理[4]考虑如下的复域常微分方程

如果p,l,m,n∈N,degP(w,w',Lw(m))＜n，

且方程满足弱 ＜p，q＞条件，那么它的所有非常数亚纯函数解w∈W，且必为下面三种形式之一：

（I）w:=R(z)是具有l(≤p)个不同的q重极点，形如

的有理函数．

（II）w:=R(ξ),ξ=eαz(α∈C)，其中R(ξ)是具有l(≤p)个不同的q重极点，形如

（III）w是在基本周期格内具有l(≤p)个不同的q重极点的双周期2ω1和2ω2椭圆函数，形如

其中℘(z)=℘(z,g2,g3)是维尔斯特拉斯椭圆函数，g2，g3分别是维尔斯特拉斯椭圆函数不变量，留数之和

3 方程(2)的求解

2.1 有理函数解

根据(4)式，我们得到方程的有理解为C：

2.2 单周期函数解

根据(5)式，我们可以得到方程的单周期函数解为：

2.3 双周期函数解

因为留数之和等于零，因此方程(2)具有双周期函数解.根据(5)式，我们得到方程的待定双周期函数解为：将此待定解代入原方程(4)，可以得到方程的双周期函数解为：

4 方程(1)的求解

根据第3 节中所给出的方程(2)的解，以及采用的变换变换

我们立刻得到方程(1)的如下的周期波解：

(3)

3 结语

本文求出的双周期波解、有理函数解和单周期波解相对于文献1-3是新的解，从数学角度讲，有理函数解是怪波解，即当s-σkt→z0时φ→∞。在一定的条件下，方程存在单周期波解和双周期波解，这些解是否能在期权市场中得到验证仍旧有待研究人员去探索，本文旨在进行数学上的探究。