大规模三维中子输运算法研究与实现

,2

1.中国科学院计算机网络信息中心,北京 100190

2.中国科学院大学，北京 100049

引言

随着核工业的持续发展与核电技术的不断进步，反应堆物理的研究与发展日益重要。反应堆物理主要研究反应堆内大量中子的统计行为，在反应堆物理中用来描述中子在介质中相互作用的，就是中子输运方程。

作为反应堆系统设计与计算的基础，中子输运方程求解方法可以分为确定论方法和统计方法。由于中子在堆内的行为与中子截面，中子运动方向，中子能量等多种因素有关，中子输运方程的求解非常复杂。传统反应堆物理以确定论方法为主。在确定论方法中，特征线方法有着高效的并行特性，且具有适用于任意维度、任意几何构造求解的优点，这使得特征线方法成为现在研究堆芯计算的主要方法。

在过去很长一段时间内，国内外对特征线方法的研究主要是在二维特征线方法上，反应堆设计和工程中也一直采用二维特征线计算作为中等保真度模拟方法，二维特征线方法发展日渐成熟。然而对于高保真建模，第三维是正确预测异质反应堆中的中子泄漏以及轴向功率分布所必需的，扩展到三维可以更精确地计算轴向泄漏和反应速率。因此科研与生产迫切需要将二维特征线方法扩展到三维。

针对将二维特征线方法扩展到三维特征方法带来的耗时、耗存储等问题，三维特征线的加速方法成为国内外研究的重要方向。然而，单纯地使用数值方法来加速特征线方法在某些情况下不收敛，随着计算规模的变化加速效果也会受到影响，因此还需进行其他加速方法的研究，并行计算就是其中最为重要的一个方法。随着计算机技术的不断进步，高性能计算成为计算加速的主要手段，并行计算也成为近十年来反应堆堆芯数值计算领域内的一个重点研究方向。因此，将数值加速方法与并行计算相结合解决三维特征线方法计算的加速问题，在学术与实际工程应用中皆具有非常重要的意义。

基于以上分析，本文使用了一种简化的几何建模方式来完成特征线的布置，即在布置特征线时只存储二维平面上特征线的信息，三维特征线的信息通过二维平面上的特征线信息来实时生成，从而大大减少了在增加第三维的情况下对内存的需求，并结合区域分解的并行方式较好的模拟了中子在介质运动过程中的能源分布情况，为实现工业级别的三维特征线方法求解程序提供了一个良好的开端。

1 中子输运方程的特征线理论方法

特征线法是求解中子输运方程的玻尔兹曼形式的一种主流方法。通过沿特征方向对玻尔兹曼输运方程将极角和方位角进行离散，并对特定方位角和极角求积的方程特征形式积分，可以得到玻尔兹曼方程的多组能群的特征形式如下

数值求解该方程近似化方法是将角度离散。首先，将方位角离散成 M 等分，同时给定不同方位角Ωm相应的权重系数wm，其中 mϵ{1,.....M}，不同方位角的角通量相加得到所求区域的标通量。其次，将极角离散成 P 等分，不同极角的权重系数为wp，其中

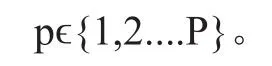
得到：

数值求解该方程的第二个近似是假设散射源是各向同性的，这使得总源可以使用标通量来表示：

数值求解该方程的第三个近似是假定每个平源区的源为常量，这意味着源沿着特征方向 k 在平源区FSGi的进入点s′与出射点s′出的源是不变的，即：

数值求解该方程的第四个近似是假设材料属性在每个平源区 FSR 上都是恒定的。

可得入射点和出射点之间通量的改变量为：

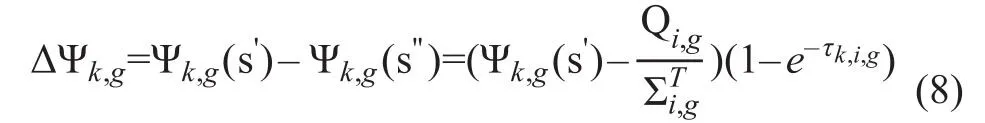
数值求解该方程的第五个近似是假设一条射线代表其附近的一小块区域。

标量通量的最终形式可以根据沿每个轨道段的角通量变化来简化得到，有：

以上就是使用特征线方法所解决的中子输运方程的解的形式。

特征线方法的迭代求解过程可以概括为以下4点：

(1)首先将整个求解区域进行网格划分。

(2)使用经过离散角度后的不同方向的特征线对区域进行扫描，计算出射线与网格的交点，从而得到每一个射线线段的长度。

(3)根据边界处已知的入射通量，逐段求出每一条射线线段的出射通量。

(4)通过散射源的内迭代和裂变源的外迭代求解直到收敛。

求解过程的流程图如图1所示。

2 特征线并行方法与实现

2.1 三维特征线生成算法

本文使用一种简化的特征线布置方式，可以大大的减少特征线布置所需的内存。首先生成径向平面内的特征线，轴向上的特征线在计算时再根据径向上的特征线实时生成。

2.1.1 径向平面特征线生成

为了保证 2D 轨道的循环缠绕，对于一个特定角度 Øi，在x和y轴上必须有整数个轨道数。

通过使用δØ的输入值，计算沿特定角度 Øi的轴的轨道整数个数：

最后校正方位角和特征线之间的距离，并用公式(1)和公式(2)校正后的值进行径向平面的特征线布置。

2.1.2 轴向平面的特征线生成

为了生成 3D 轨迹，除了产生 2D 轨迹所需的参数之外，还需要轴向上轨迹间隔δθ和0＜θ＜π的极角数目nθ。利用这种方法创建极角来均匀地细分角度空间，使得 0＜θ＜π/2 中的每个极角与互补的极角配对。

其中θi,nθ-j-1是角度θi,j的补角。

为了保证三维轨道的循环轨道缠绕，必须满足两个条件：

(1)对于每个方位角 Øi，极角θi,j和2D 轨道周期沿着 2D 轨道周期的3D 轨道投影的开始和结束之间的距离必须是轨道间隔整数倍。

(2)对于每个方位角 Øi和极角θi,j，必须在几何深度Δz 上沿着 z 轴具有整数倍的轨迹间隔。

第一个条件保证当 2D 反射周期完成时 3D 轨道周期回绕到另一个3D 轨道上。第二个条件保证当周期完成时，包含顶面或底面反射的3D 轨迹周期。

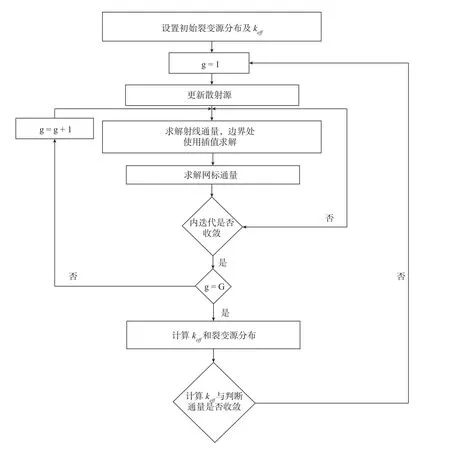
图1 迭代求解算法流程Fig.1 Iterative solution algorithm flow

2.1.3 三维全局射线追踪方法

使用每个方位角的循环轨道周期长度，可以计算在一个完整的2D 周期之后在一组 3D 轨道的开始和结束之间的轨道间隔的整数倍:

然后需要将沿着 z 轴的轨道间隔的数量设置为整数倍。通过考虑 z 方向上的轨道间隔的数量与沿着2D 轨道长度间隔之间的关系可以找到z 轴上的轨道的数量：

从而得到z 轴上特征线之间的距离：

最后校正极角和特征线之间的距离，并用使用公式(2.10)和公式(2.11)校正后的值布置轴向的特征线。

2.2 基于区域分解的并行设计

本文实现的程序采用 MPI 编程模型，并结合区域分解的并行方式。

空间分解采用分布式存储模型,这对缓解完整核心问题所需的内存负担是必要的。空间分解背后的基本思想是将完整的核心问题分成足够的空间域，以便每个域的大小都可以在单个进程中管理。为了实现空间域分解，主要问题是跨空间子域边界传递边界条件信息的开销。图2 展示了在二维空间中，特征线在边界处的数据交换，除非引入近似值，否则特征射线必须跨越这些边界直接连接，以便传输界面角通量。

从特征线方法可知特征线方法的并行方式可以从能群、角度、射线以及几何区域选取，结合本文所使用的特征线布置方式，本文采用区域并行的方式，使用 MPI 提供的切割函数，将求解的几何区域进行切分，将分解后的各个子区域分配至不同的进程，从而减少每个进程上的计算量。如图3所示，这里假设将求解区域划分为4个子区域。

上图的4个子区域分配到对应的4个进程上，进程间在反射边界进行数据通信，每个进程可以接受来自上下、左右、前后 6个方向进程的数据，进程间数据交换的示意图如图4所示。

其中 scr_id为源进程号，myid为当前进程号，dest_id为目的进程号，f_psi、b_psi 分别代表消息传递的前后方向。

图2 边界数据交换Fig.2 Boundary data exchange

图3 区域分解示意图Fig.3 Area decomposition diagram

2.3 基于三维特征线方法的并行求解器

基于三维特征线方法的并行求解器的核心算法主要包括特征线的生成、几何区域分解、传输扫描算法、进程间数据通信。

2.3.1 特征线生成

特征线的生成是求解的第一步，它涉及径向平面的特征线生成和轴向平面的特征线生成两个方面。首先是径向平面的特征线生成过程：根据输入的方位角的个数以及特征线之间的间隔来生成特征线，为不同方位角的特征线分配不同的权重，表1给出了二维平面特征线生成的伪代码算法。

根据径向平面某一方向的特征线作为轴向特征线在径向上的投影，轴向上根据不同极角来生成特征线。表2给出了轴向平面特征线生成的伪代码。

图4 进程间数据交换示意图Fig.4 Schematic diagram of data exchange between processes

表1 径向平面特征线生成算法伪代码Table1 Radial plane feature line generation algorithm pseudo code

2.3.2 几何区域分解

本文中使用 MPI_Cart_create 函数来分割需要求解的区域，然后通过 MPI_Cart_shift 函数来获取当前进程的相邻进程号，表3给出了相应的伪代码算法。

上述伪代码中 ndims 表示划分后的维度，ndims表示不同维度分配的进程数，period表示进程通信是否首尾相邻。

2.3.3 扫描迭代算法

扫描迭代算法是整个程序的核心部分，其主要是计算对于某个网格内某一方向上的特征线对该网格的贡献度，即平均角通量，然后通过对不同方向的贡献度进行规约计算得到该网格的标通量的一个过程，最后通过平均角通量来更新散射源的内迭代和通过标通量来更新裂变源的外迭代来求解问题知道问题收敛。更具体而言，对于某一条具体的特征线，其主要是计算该条特征线在网格内的通量改变量，从而得到不同方向的平均角通量。表4 列出了单次特征线扫描迭代算法。

表2 轴向平面特征线生成算法伪代码Table2 Axial plane feature line generation algorithm pseudo code

上述传输扫描算法涉及方位角、轨迹、不同FSR中的段，能量组和极角上的五个嵌套环路伪代码中符号 m、k、s、g、p 分别表示方位角号、特征线号、线段号、能群号、极角号；相对应的大些字母表示其集合。

在计算完某网格内的平均角通量后，我们需要更新散射源和裂变源，以此来判定问题是否收敛。表5中给出了如何更新源的伪代码。

2.3.4 边界数据通信

每个进程内都单独的进行传输扫描算法，当传输扫描算法结束后在边界上进程间需要进行数据通信，从而在进行下一轮的传输扫描算法，表6给出了进程间数据通信的伪代码。

上述伪代码中 Send Buffer、Recv Buffer 分别代表发送和接收消息的队列，Number of Elements 代表发送的数据大小，send_dest[i]、rec_sources [j]分别代表目的进程号和源进程号。

表3 几何区域分解算法伪代码Table3 Set region decomposition algorithm pseudo code

表4 特征线扫描算法伪代码Table.4 Feature line scan algorithm pseudo code

表5 源更新算法伪代码Table.5 Source update algorithm pseudo code

表6 进程间数据通信算法伪代码Table6 Interprocess data communication algorithm pseudo code

3 程序性能测试与分析

3.1 测试平台

测试平台为中科院计算机网络信息中心的超级计算机“元”上的部分节点，节点的具体配置表如 7所示。

我们分别对程序进行了弱扩展、强扩展二个方面的性能测试，一个进程运行在一个节点上，具体测试结果见后续小节。

3.2 弱扩展性测试结果

弱扩展性的测试分别在1个进程、2个进程、4个进程、8个进程、16个进程下进行测试，相对应的测试规模如表8所示。

测试结果结果如图5所示。

由图5 可知，随着求解规模的增大，程序运行时间略有上升，但整体的求解时间并没有大幅度的波动，这一定程度上表明我们程序的弱扩展性较好。

表7 测试平台参数Table7 Test platform parameters

表8 弱扩展测试程序规模参数表Table8 Weak extension test program size parameter table

图5 弱扩展测试效果图Fig.5 Weakly extended test renderings

表9 强扩展测试程序规模参数表Table9 Strong extension test program size parameter table

表10 相对单个进程运行时间的时间加速比Table10 Time-to-acceleration ratio relative to the running time of a single process

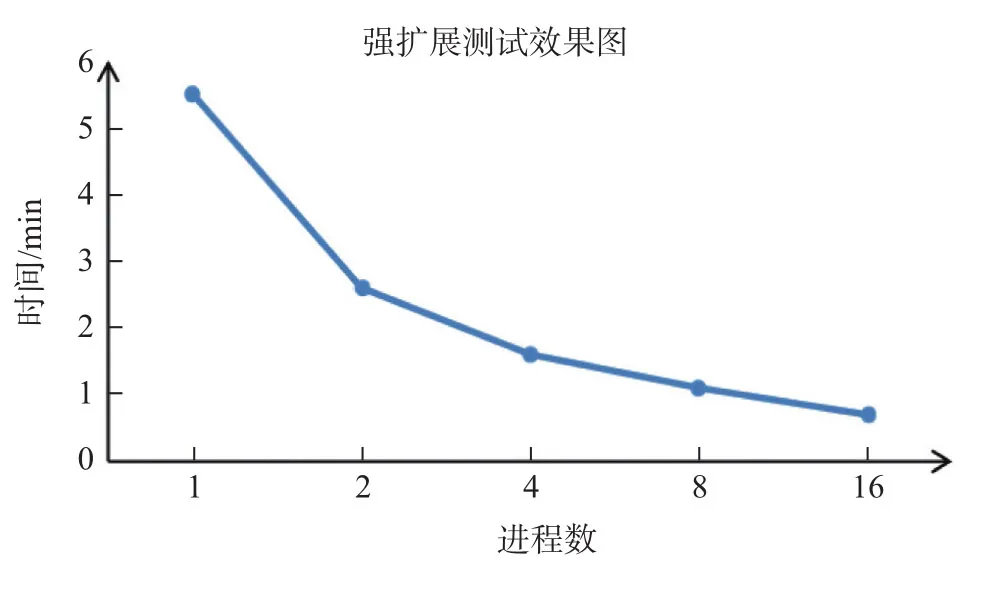
图6 强扩展测试效果图Fig.6 Strong expansion test renderings

3.3 强扩展性测试结果

强扩展性的测试分别在1个进程、2个进程、4个进程、8个进程、16个进程下进行测试，测试规模参数如表9所示。

测试结果如图6所示。

表10给出了随着进程数增加实际的加速效果比。

由图6 与表10 可知，在求解问题规模不变的情况下，求解的时间随着进程数的增加而减少。在4个进程以内时，程序表现出很好的扩展性，但是在扩展到8个进程以上时，由于每个进程分到的计算量太少而无法重复发挥每个节点的性能，导致程序的并行效果受到影响。

4 总结

作为核反应堆系统设计与计算的基础，堆芯计算的方式在一直不断地得发展。在反应堆计算的诸多数值方法当中，特征线方法以其良好的并行性、几何适应性强等优点，成为国内外研究的重点。

本文实现了一个基于三维特征线方法的求解中子输运方程的计算程序，并 将该程序在多核 CPU 节点上进行测试。实验结果表明程序的强弱扩展性、加速比都达到了预期的效果，为后续设计更加复杂的利用三维特征线方法计算中子输运问题打下良好的基础。