随机通货膨胀下DB养老金计划风险管理—Funding期权和Buyout期权及其定价

安徽工程大学数理学院，安徽 芜湖，241000

1 引言

养老金计划可以分为DB计划和DC计划。在DB养老金计划下，员工的退休金的额度将会在其加入DB养老金计划时给定，因此计划的投资风险主要由DB养老金计划发起人承担。罗伊(Roy，2012)[3]指出DB养老金计划主要面临人口和市场变动的两大风险。

在过去十年里，空前的市场波动和利率的持续下降，一连串的坏消息使许多DB计划的发起人遭受了巨大的损失。Cox 等人(Cox，2013)[4]发现死亡率的意外提高增加了DB养老金的负债，面临着严峻的养老基金赤字问题。其结果是，Coughlan 等人(2013)[5]发现近几年DB养老金计划发起人对用策略来减少他们DB养老金风险的兴趣逐渐增加。Lin 等人(Lin，2015)[1]提出用长寿对冲和DB养老金收购(buyout)来减少DB养老金风险。王晓军等人(王晓军，2018)[6]从保险公司风险管理的角度看，长寿风险使得保险公司的未来负债增加，特别是在长期低利率环境下，长寿风险的影响更加突出。与这一观察一致，Lin 等人(Lin，2017)[7]发现，在企业风险管理框架中收购比长寿对冲创造更多的价值。陈翠霞等人(2018)[8]基于buyin和buyouts 进行DB养老金计划去风险化研究并对其定价。Cox 等人(Cox，2017)[2]研究创新的方法去获得资金不足的DB养老金计划的DB养老金收购在提升价值上的途径，他们提出两种期权，即DB养老金基金期权(funding 期权)和DB养老金收购期权(buyout 期权)。

公认的期权定价理论创始人是法国数学家 Louis Bachelicr。现代期权定价理论的革命发生在1973年，美国金融学家 Black和Scholes[9]在有效市场和股票价格遵循几何布朗运动等一系列假设条件下，运用连续交易保值策略推出了 Black-Scholes 定价模型。Cox 等人(Cox，2017)[2]的这篇文献展示了如何明确地为这些期权定价，可获得的公开预测死亡率表由Lee和Carter(1992)[10]的死亡率模型统计。Cox 等人(Cox，2013)[11]他们的工作促进了越来越多的DB养老金去风险研究，DB养老金套期保值政策被认为是由风险转移所需的风险溢价、搜索和信息成本等交易成本以及监测和执行合同执行的成本决定的。

本文主要基于Cox 等人(Cox，2017)[2]提出的两个期权定价方式作进一步改进，在计算DB养老金资产指数时，将随机通货膨胀率考虑进去，本文假设通胀风险由服从几何布朗运动的物价指数来度量。目前现有的文献还没有考虑通胀在DB养老金风险定价的影响。与目前现有文献相比，本文的创新点表现为以下三个方面：(1)本文研究的两个期权有利于减少DB养老金风险，对DB养老金风险管理的文献进行补充。(2)为了增加市场的流动性，减少道德风险和逆向选择问题，引入一个透明的DB养老金基金指数基于市场指数、公开可获得的死亡率表和DB养老金强制性缴费。(3)我们为目前的DB养老金风险定价研究做出贡献，我们展示了如何为这些新的DB养老金去风险化证券定价，同时认识到投资风险、通货膨胀风险、长寿风险和利率风险。

2 基本框架

2.1 DB养老金负债指数

DB养老金负债指数是基于一组年龄为x0人数为N(0)的退休群体。为确保透明度，在计算t时DB养老金负债指数时，我们根据预测的未来死亡率使用一个公开的人口死亡率表。假设队列中的每个幸存成员每年都获得P的生存福利，并在每年年底支付。对于给定的计划，在时间t=0 时，我们可以使用N(0)队列成员的平均年福利。然后，PLIt是在t时向N(t)个未亡退休人员支付的所有未来养恤金的现值：

在时间t=0 时，已知退休人员人数N(0)和年费P。因此，在0 时刻，PLI0是已知的：PLI0=N(0)·Pax0。在(1)中，ax0+t是年龄x=x0+t在t时刻给定的预测死亡率的生存贴现因子：

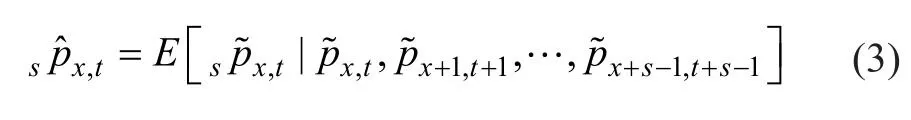
DB养老金负债的价值与长期企业债券的收益率密切相关，正如 GüKaynak 等人(2005年)[12]指出的那样，“由于许多宏观经济数据的发布和货币政策公告，长期远期利率大幅波动”。虽然 Cox(Cox,1985)[13]和Hull and White(Hull and White,1990)[14]文献中存在各种短期利率模型，但很少有人提出简单有效的模型来捕捉长期利率的变化。在本文中，我们谨慎地使用CIR 模型(Cox,1985年)[13]来说明DB养老金估值率的动态变化。即DB养老金估值率满足以下过程：

其中v是平均回归率，θ和σp是DB养老金估值率的长期均值和瞬时波动率，是一个标准的布朗运动。通过控制参数σp，DB养老金估值率的波动相对平稳，有望与长期利率行为相一致。利用 2001年1月至2010年12月的美国国税局综合公司债券利率月度数据，我们得到了表1所示的最大似然估计数。

2.2 DB养老金资产指数

假设DB养老金资产指数PAIt是由t时刻的三个指数组成：美国标准普尔 500 指数(i=1)、美林公司债券指数(i=2)和3个月国债指数(i=3)，其权重分别为ω1，ω2和ω3。在物理风险测度下(P)，标普 500 指数在t时刻的过程A1,t由下面这个随机微分方程描述

其中α1是标普 500 指数的瞬时期望回报，σ1是标普500指数的瞬时波动率 。是均值为0 方差为t的标准布朗运动，λ1为泊松过程N1t单位时间内的抵达率，独立同分布大小V1j，j=1,2,...被建模为对数正态随机变量，因此，它的对数Y1j=logV1j是一个均值为m1、标准差为s1的标准正态随机变量。泊松事件将导致标普 500 指数中预期的百分比改变相当于k1=E(V1j-1)。随机微分方程(5)的解为：

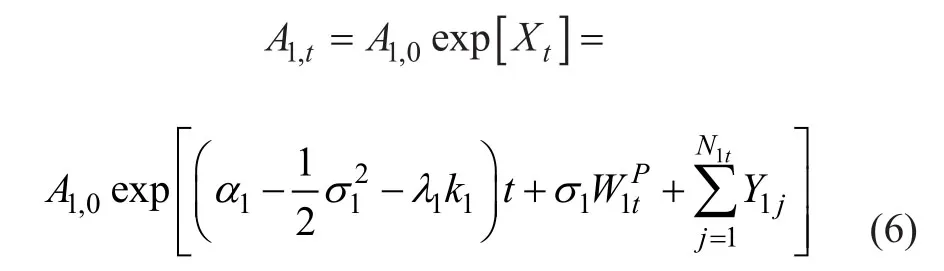
为了在测度变化下保持相同的跳跃扩散框架，我们遵循 Gerber和Shiu(1994)[15]的方法，采用对数资产收益的必要变换作为鞅等价测度，证明了这种风险中性测度是最接近的鞅等价测度。通过其相应的Radon-nikodym 导数定义风险中性 Esscher 测度P*(Xt,h)为：

表1 DB养老金估值率的最大似然参数估计Table1 Estimation of maximum likelihood parameter of BD pension estimation rate

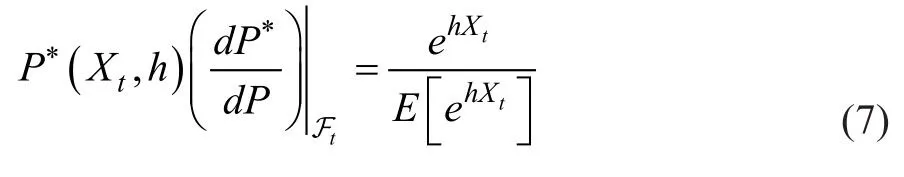
其中h是常数，使得存在。

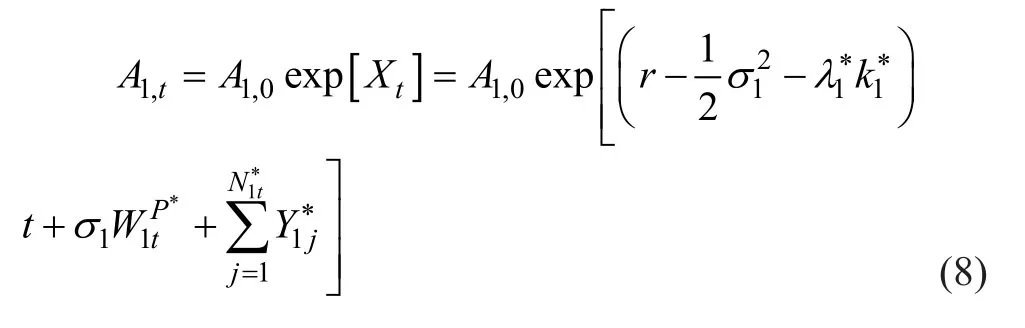
其中r是无风险利率，是一个P*测度下的标准布朗运动，并且新的泊松和跳跃大小参数是：

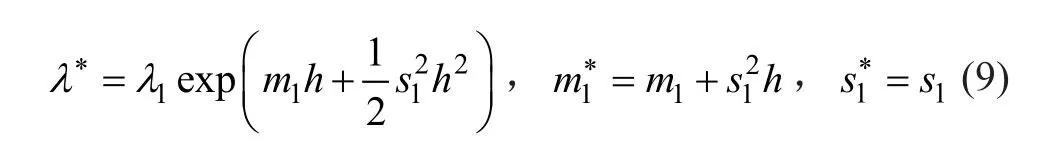
确定了参数h，使得是关于Esscher 风险测度P*的鞅。更具体地说，参数h满足：

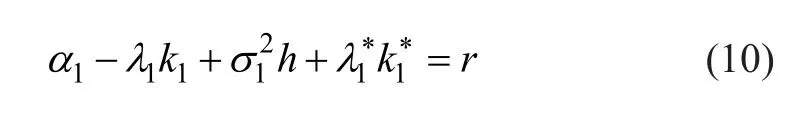
这种物理风险测度和风险中性 Esscher 测度下的参数之间的显式解析关系为第5 节的数值说明提供了很大的方便。

美林公司债券指数和3个月国债指数(i=3)的动态过程被建模为几何布朗运动：

其中常数α2(α3)是美林公司债券指数(3个月国债指数)的漂移项，其瞬时波动率为σ2(σ3)。在(11)和(12)中的是均值为0 方差为t的标准布朗

假设资产的价格X(t)可表示为：

大量的事实证明，在市场经济条件下，通货膨胀是时有发生的，我们假设通货膨胀是随机过程，其价格水平Qt服从如下的随机微分方程：

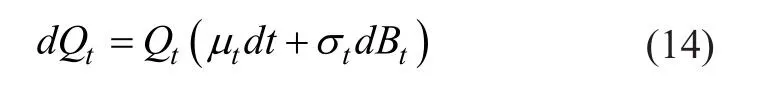
命题1 如果标普 500 指数在t时刻的过程A1,t满足随机微分方程(5)，美林公司债券指数(i=2)和3个月国债指数(i=3)的动态过程满足几何布朗运动(11)，则基于通货膨胀风险(14)下的随机方程(15)的解为：

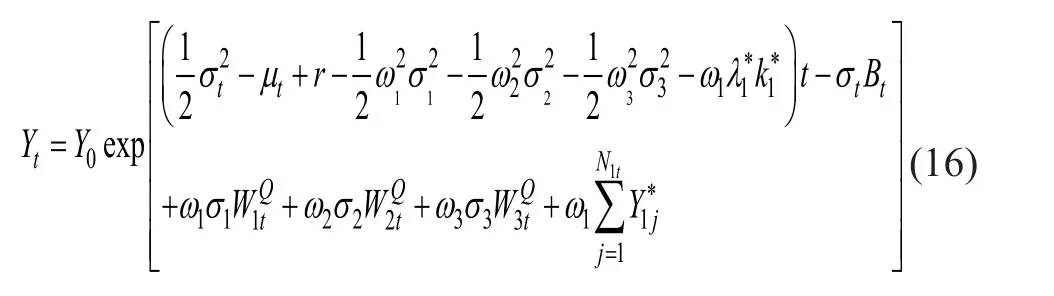
证明

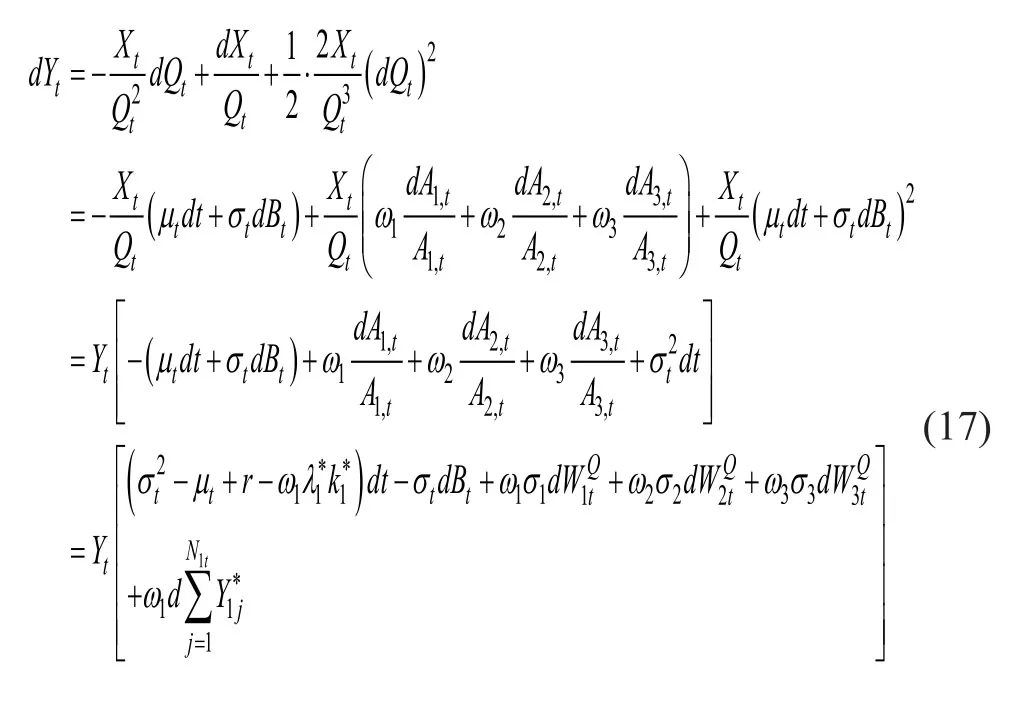
其中ω1+ω2+ω3=1，根据几何布朗运动求解公式(17)解得：

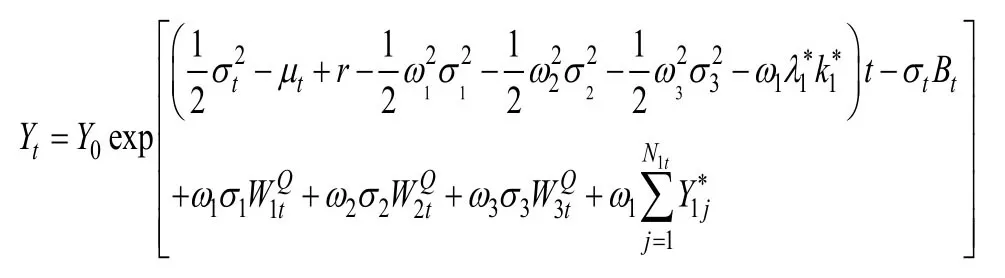
DB养老金资产指数PAIt是由指数I在时间t组成的市场投资组合的价值决定的。即

为了增加模型校准的观测量，我们利用 1988年1月至2010年12月的月数据估计了这三个指标的(6)和(11)中的参数。美国标准普尔 500 指数、美林公司债券指数和3个月国债指数的月度历史数据都是从数据流中获取的。由于建议的退休金方案只有在每年年底才可行使，所以我们将每月的估计数转换为按年计算的估计数。表2 报告了年度最大似然估计数。

2.3 DB养老金基金指数

基于指数证券化降低了道德风险和逆向选择，增加了流动性，降低了交易成本，并提供了一个标准化和透明的结构。具体来说，t时刻的DB养老金基金指数PFIt是指DB养老金资产指数PAIt与DB养老金负债指数PLIt的比率：

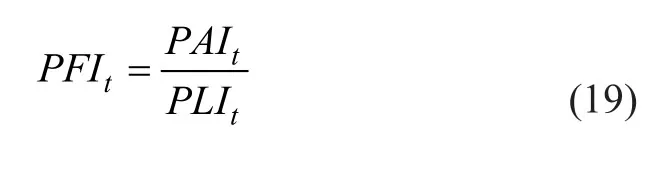
由于我们在计算DB养老金资产指数时考虑了通货膨胀，这因此就改变了DB养老金基金指数，下面我们来讨论通货膨胀下的DB养老金基金期权和DB养老金收购期权的定价方式。

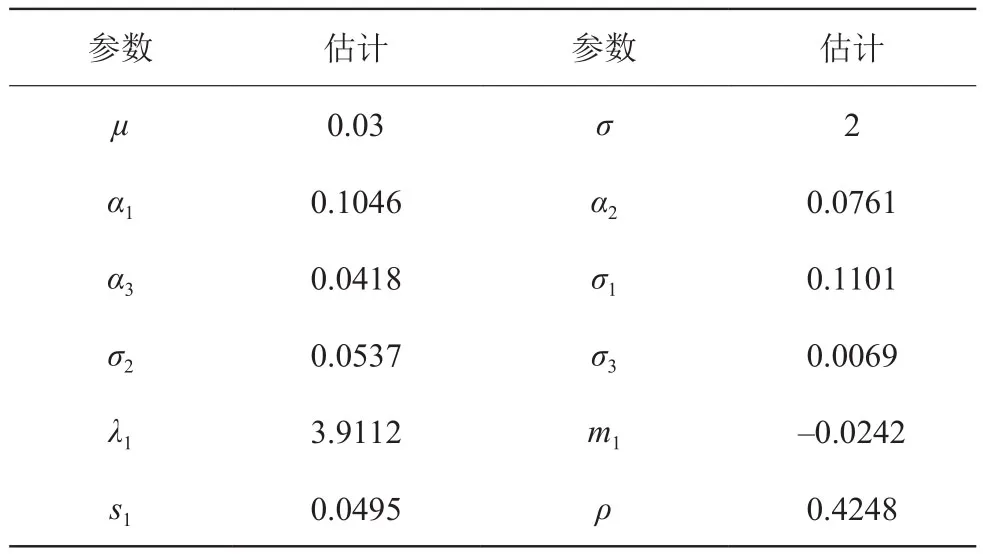
表2 三种资产指数的最大似然参数估计Table2 Estimation of maximum likelihood parameters of three asset indexes

3 DB养老金期权定价

根据上述DB养老金资产和负债指数模型，可以使用传统的风险中性定价技术对基金和收购期权进行估价。

3.1 资金充足计划下的DB养老金期权

考虑一项DB养老金计划，该计划在0 时刻得到全额资助。假设其资金状况与DB养老金基金指数PFIt高度相关。为了管理其DB养老金基金风险，该计划可以购买以下的n年基金期权，并设置敲定水平K。期权定义为名义金额NA、可行使期权的触发基金指数z，当敲定水平K＞z。它可以在时间t=1,2,...,n时被执行，当且仅当PFIt＜z，t时刻的收益概述如下：

我们定义了第二个期权，它识别收购提供者的风险溢价，如下所示，与触发水平z、敲定水平K和期限n的定义相同。这一收购期权提供了一个目前资金充足的计划，在t时有以下回报：

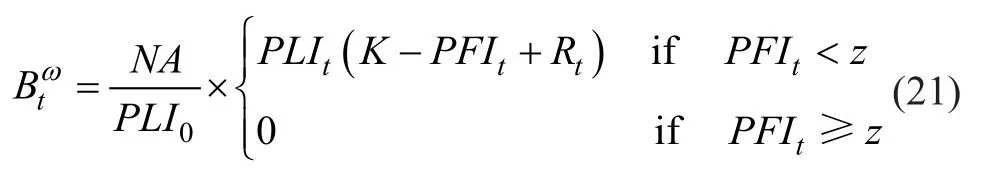
其中Rt是t时刻估计的收购风险溢价。在(11)中，这种收购期权的收益高于基金期权。因此，收购期权的价格将高于基金期权。

3.2 资金不充足计划下的DB养老金期权

与资金充足的DB养老金计划不同的是，资金不足的计划可能没有立即进行收购的现金。为了使DB养老金收购可行，这样的计划可以购买具有敲定水平和名义金额的年期基金期权，但必须满足当。以下表达式描述时间处此期权的值：

资金不足的公司可能希望在基金比率达到z后立即进行收购交易。在资金完全到位的情况下，我们引入了一种确认的提供者的风险溢价的收购期权。对于这种资金不足的计划，收购期权的回报，但在时间t的定义如下：

3.3 期权定价

给定期权收益函数(19)，资金充足的DB养老金的n年基金期权的风险中性价格(按名义金额的百分比计算)可以表示为

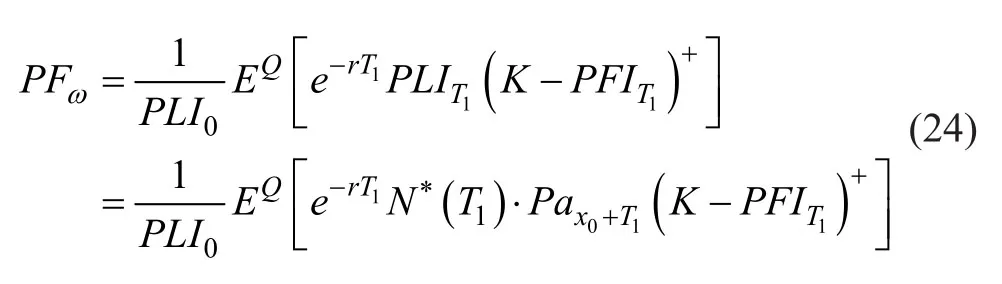
其中T1表示第一个观察到的年底，即DB养老金基金指数低于触发水平z。DB养老金群体N*(t)在(23)中的生存演化是基于转换后的死亡率，以反映市场对死亡率改善的预期。

如果在基金期权的顶部添加了直接收购功能，且结构完全相同，则n年收购期权的价格将由下式给定

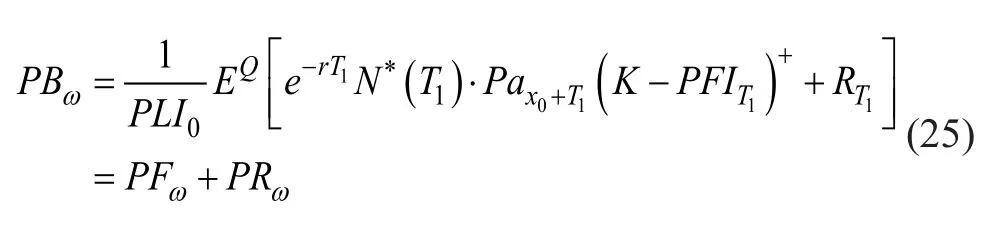
其中

是收购功能的期权溢价。请注意，Rt是一个在时间t时资金充足的DB养老金计划的立即收购溢价。据 Lin 等人(2017b)[16]，Rt可以分解为投资风险溢价和长寿风险溢价。更具体地说，考虑到PAIt=PLIt在t时刻，

其中立即收购投资风险溢价Pinvest,t由下式给出

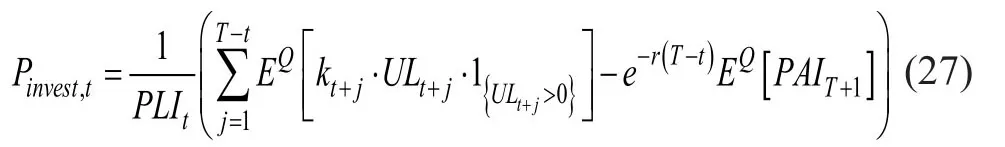
其中

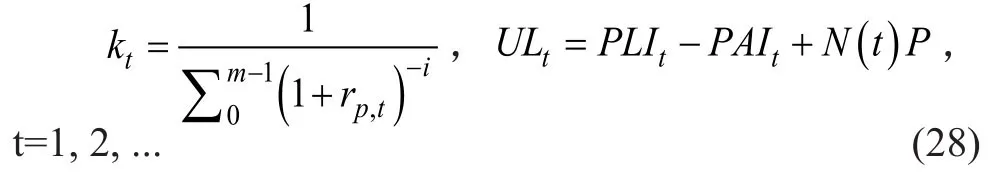
及时收购长寿风险溢价Plongevity,t如下

为了获得DB养老金基金和收购期权的价格，我们需要使用反映市场对未来死亡率改善的预期的转换死亡率。我们使用 Wang 变换来扭曲死亡率。要转换的随机变量是生命年龄x在时间 0 时的剩余寿命时间T(x,0)。该变换适用于其从而得到转换后的cdc如下：

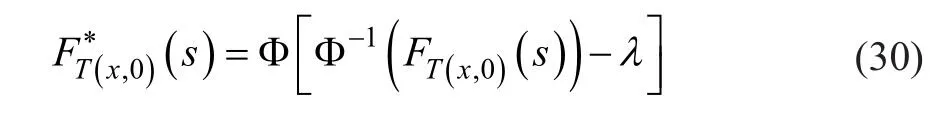
其中累积概率

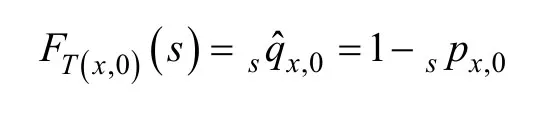
是一个生命年龄x在时间上 0 在s年内死亡的概率。在(29)中，λ＞0 是系统长寿风险的市场价格。Ф(·)是标准正态cdf。经过变换，我们可以得到年龄为x的风险中性的s年生存率用于定价：

同样，根据(21)中定义的资金不足计划的n年基金期权收益可以获得期权价格通过

其中T2表示第一个观察到的年底，即DB养老金基金指数超过触发水平z。最后，对于资金不足的计划的n年基金期权收益可以获得其价格是

其中

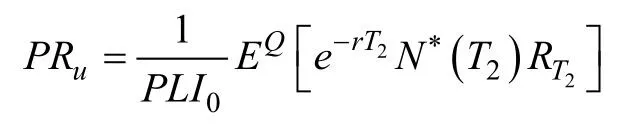
也是收购附加的溢价。

4 数值计算

假设时间为0 时刻，W 公司的所有计划参与者都达到退休年龄x0=65，每名退休人员只要是在每年年底还活着，每年可领取 60000 便士的生存津贴。这个群体假设有N(0)=5000 名退休人员在0 时刻与美国男性人口有相同的死亡经历，因此，它遵循了DB养老金负债指数PLIt在(1)中的相同动态。进一步假设W 公司最初将其DB养老金资产的比例ω1=0.5 投资于美国标准普尔 500 指数、ω2=0.45 投资于美林公司债券指数和ω3=0.05 投资于3个月国债指数在0 时刻时。我们进一步假设 W 公司选择在每年年底将其资产配置重置为初始权重。

在0 时刻，W 公司的DB养老金计划资金充足，基金比率为1。为了对冲未来面临资金限制时无法弥补严重资金赤字的风险，公司以t=0 时的价格购买了一个终身DB养老金基金期权。该期权允许公司在整个计划的整个生命周期内，当DB养老金基金指数PFIt低于触发级别z时行使该期权。当在t时刻触发此基金期权时，给定敲定水平K，W 公司将获得由(19)确定的报酬。

假设 0 时刻的DB养老金估值率为rp,0，长期无风险率低于1%，等于r=0.047。在(23)中，我们计算了不同触发水平z和敲定基金比率K下的基金期权溢价PFω。结果见表3。当触发水平为z=0.8，敲定水平为K=1.00 时，如果基金指数PFIt降低到80%，W 公司将行使此期权。当这种情况发生时，该期权将支付足以弥补整个资金短缺的款项，因为该计划的供资状况遵循PFIt。为获得这一期权，在0 时刻按初始DB养老金负债比例PLI0表示，W 公司支付保险费等于PFω=11。28%。

W 公司可以购买具有不同触发和敲定水平的其他基金期权。由于触发和敲定水平下降，基金期权溢价也会下降。这是因为它不太可能触发该期权，如果该期权被触发，则该期权的回报较低。例如，如表3所示，当触发级别z从 0.8 降至0.7，敲定基金比率K从 1.00 降至0.90 时，基金期权溢价PFω从 11.28% 降至6.08%。

如果在未来出现严重的资金赤字后，W 公司很难为退休人员的DB养老金提供资金，那么它可能想通过收购来降低DB养老金的风险。然而，在这种情况下，DB养老金收购成本将高得令人望而却步。除了用现金注入来弥补资金赤字外，W 公司还必须支付收购风险溢价。为了对冲这一风险，W 公司可以购买DB养老金收购期权。表3的最后一列显示了在给定触发水平下购买收购期权的风险溢价价格PRω。例如，当触发器z=0.8 时，买断附加成本PRω=5.62%。这意味着 W 公司需要支付 16.90%(PFω+PRω=11.28%+5.62%)的溢价才能购买这种收购期权。这种收购期权允许 W 公司在养老基金指数降至z=0.8 时将其全部DB养老金负债转移给期权卖方。类似于基金期权的模式，收购期权的价格随着触发水平的降低而下降。当触发水平z从 0.8 降至0.7 时，收购期权溢价PRω从 16.90%(PFω+PRω=11.28%+5.62%)降至12.35%(PFω+PRω=9.21%+3.14%)。

对于资金充足的养老公司来说，收购期权是否很昂贵？为了回答这个问题，我们在第0 时间比较了收购期权和即时DB养老金收购的成本。跟踪Eqs.(25)-(28)，如果公司将其DB养老金义务在0 时转移给收购风险承担者，则我们获得的收购价格等于R0=13.83%。当触发点为z=0.8 时，收购期权溢价为PRω=16.90%。虽然收购期权要求的现金流出要高于0 时刻收购，但当期权被触发时，它提供了额外的保护，弥补了整个资金赤字，至少占DB养老金负债的22.20%。如果将触发因素降低到z=0.7%，则收购期权的总成本仅为PRω=12.35%，低于即时收购R0=13.83%的价格，如果 W 公司只想在最需要保护的时候转移DB养老金风险，就可以购买低触发水平的收购期权(例z=0.7)。

与像 W 公司这样的计划资金充足的公司相比，资金不足的公司可能希望从资产负债表中消除DB养老金负债，因为强制性DB养老金缴款会带来巨大的财政负担。随着DB养老金收购，他们不得不等到他们的计划得到充分的资金，他们有财政资源支付买断风险溢价。收购期权使得DB养老金收购变得越来越容易。假设 U 公司的DB养老金计划与 W 公司的DB养老金计划成员和资产组成相同，但在第0 时其资金不足 20%(基金比率为PFI0=80%)。它购买了一个终身基金期权，当DB养老金基金指数PFIt提高到触发水平z时，该期权提供资金。具有不同触发和敲定水平的终身基金期权的价格如表4所示。考虑到具有再平衡的固定权重，如果 U 公司购买一个触发水平z=0.85、敲定水平K=1.00的终身基金期权，则需要支付PFu=6.82%的基金期权溢价。当DB养老金基金指数PFIt提高到0.85 时，这一基金期权将覆盖全部资金赤字。如果 U 公司希望在期权被触发时进行收购，它将需要支付额外的收购附加溢价PRu=6.12% 来实现这个目标。在这种情况下，DB养老金收购期权的总溢价为PBu=12.94%(=PFu+PRu=6.82%+6.12%)。请注意，与立即收购相比，它要便宜得多，后者将花费 33.83%(=20%的资金赤字+13.83%的收购溢价)。如果 U 公司选择一个触发率更高的收购期权，那么DB养老金收购期权的成本就会更低。例如，当z=0.9 时，收购期权溢价降至PBu=7.72%(=PFu+PRu=2.96%+4.76%)。

我们还发现，基金和收购期权溢价随着初始基金比率PFI0而降低。例如，当z=0.90，K=1.00，z=0.9 时，基金(收购)期权溢价为2.08%(6.05%)，低于PFI0=0.8，2.96%(7.72%)。这是因为资金严重不足的计划更难改进和触发给定的触发水平z。因此，对于z和K的每一个组合，对于资金不足的计划，基金和收购期权都比较便宜。

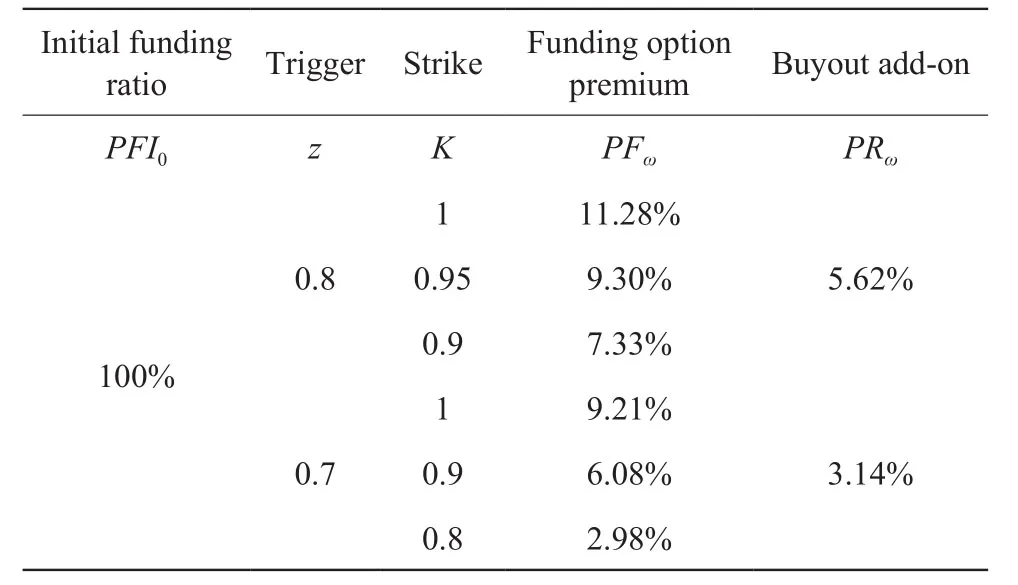
表3 资金充足计划的终身基金和收购期权溢价，并不断调整权重Table3 Lifetime fund and acquisition option premium for fund-sufficient programs,and constantly adjust the weight

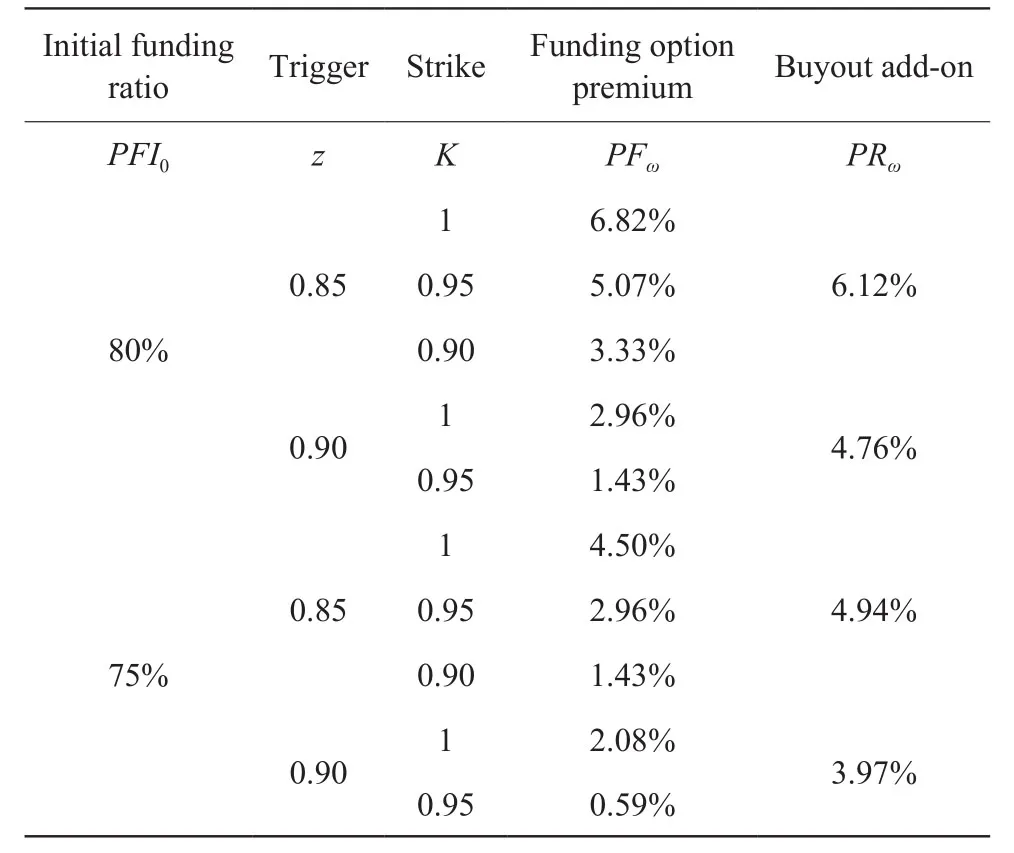
表4 资金不足计划的终身基金和收购期权溢价，并不断调整权重Table4 Under-funded plan life fund and acquisition option premium,and constantly adjust the weight

5 结论

本文考虑通货膨胀服从随机微分方程，在计算DB养老金资产指数时，把通货膨胀考虑进去，会使得计算出来的期权价格更符合实际情况。首先对DB养老金资产指数和DB养老金负债指数的演化进行了建模，得到了养老基金指数的动态变化。然后，我们计算了保险公司承担DB养老金资产收益不确定风险的投资风险溢价和长寿风险溢价，这种风险解释了DB养老金参与者寿命比预期长的风险，并将通货膨胀风险考虑进去，在计算DB养老金资产指数时加入通货膨胀。经过计算，加入通货膨胀后的期权价格会比 Cox 等人(Cox,2017)[2]计算出期权价价格高。在对于DB养老金计划资金充足与不充足两种情况进行了分情况讨论，我们证明，对于资金充足的计划来说，DB养老金期权会为其提供推迟收购的时间，而对于资金不足的计划来说，DB养老金期权是一种成本效益高的方式，可以更快地进行收购。为了证明我们的结果的稳健性，我们探讨了一个参数中的值变化如何影响DB养老金期权价格。数值算例验证了定价模型的可靠性，得到了合理的结果。