飞行型绳牵引并联机器人气动特性计算与分析*

苏 宇，赵 鹏，李沁洋，王 沁

(西安工业大学 机电工程学院，西安 710021)

飞行型绳牵引并联机器人包含四旋翼无人飞行器和绳牵引并联机器人两个子系统，在广阔区域上空自由飞行，克服了传统基座固定型绳牵引并联机器人工作区域固定的缺陷[1]。四旋翼飞行器提供空中飞行能力；绳牵引并联机器人通过绳索悬吊于四旋翼无人飞行器下方，通过绳索收放控制动平台位姿。飞行型绳牵引并联机器人气动特性是在飞行过程中所受升力、阻力、受力方向及飞行稳定性等影响飞行的客观因素，是计算空气动力，检验气动布局设计合理性和进行飞行控制的理论基础，起到保证系统的飞行特性及性能的重要作用[2-4]。

传统的气动特性分析主要是通过理论计算和风洞试验。理论计算由于飞行器外形和边界条件的复杂性、方程的强耦合性和高度非线性，导致建模和求解困难，因此仅适用于飞行器外形规则且边界条件简单的情况[5]；而飞行型绳牵引并联机器人增加了悬吊结构，且绳索为柔性单元，因此建模与求解非常困难。风洞实验可最大限度地模拟真实气动条件，多为一些大型科研机构所采用。文献[6]采用极大似然估计和最小二乘法，利用全尺寸风洞的实验测量数据来估算无人飞行器的纵向气动系数。文献[7]通过美国国家航空航天局(National Aeronautics and Space Administration,NASA)的亚音速风洞测试了一种全翼短距起落型飞行器样机，得到其气动参数。文献[8]利用德荷风洞，在跨声速条件下验证了一种全跨度比例商务喷气式飞机模型的气动性能。风洞造价高昂、维护成本高和建设周期长的问题不容忽视。计算机性能和计算流体力学软件的发展使得气动力学的计算机仿真成为可能，可较为真实地模拟实际场景，缩短研制周期，减少实验成本[2-3]。文中采用计算流体力学软件Fluent进行飞行型绳牵引并联机器人的建模和仿真，通过选择求解器、湍流模型，设定飞行速度、攻角、大气温度和压力等边界条件进行仿真，得到升力系数、阻力系数、俯仰力矩系数和表面压力分布，通过仿真结果的对比与分析来研究其气动特性，从而为飞行型绳牵引并联机器人的结构优化及运动控制提供理论依据。

1 气动特性分析基本理论

飞行型绳牵引并联机器人的飞行过程受到两方面作用：一方面旋翼旋转使得气流反作用于系统各部件，由于表面压力分布的不均匀性，导致压力差出现；另一方面气流流过飞行器表面会产生黏性摩擦力。压力差与黏性摩擦力共同作用形成空气动力。飞行过程中的升力L、阻力D和俯仰力矩M是研究空气动力特性的重要气动参数[9]，其力学表达式为

式中：CL，CD，CM为升力系数、阻力系数和俯仰力矩系数，为无量纲比例系数，统称为气动力因数；ρ为空气密度；V为飞行速度；q为来流动压；S为系统最大横截面积。在给定飞行型绳牵引并联机器人外形、飞行速度和攻角(即迎角)等条件后，ρ，V，q，S为定值，由式(1)可知系统在飞行过程中所受空气动力取决于气动力因数。

由于飞行型绳牵引并联机器人各部分结构不同，空间气温不断变化及空气密度差异等因素导致在飞行型绳牵引并联机器人的表面形成了湍流。湍流是流体的一种流动状态，对四旋翼无人飞行器所受的空气动力产生很大的干扰，因此需要选择合适的湍流模型，以便模拟实际飞行过程中气流对空气动力的影响。由于飞行型绳牵引并联机器人飞行速度较小，马赫数Ma约为0.10，且外形尺寸不大，因而其飞行具有雷诺数低和黏性摩擦小的特点，属于有边界层的湍流。因而本文采用对边界层计算效果较好且计算量相对较小的单方程(Spalart-Allmaras)湍流模型，其输运方程如下：

2 气动特性计算模型

2.1 仿真模型与计算域模型建立

飞行型绳牵引并联机器人的主要结构包括旋翼、机架、电子舱、支撑环、绳索和动平台。在Solidworks软件中建立飞行型绳牵引并联机器人的三维模型后导入到Fluent软件中。模型的形状突变和微小部位及孔洞、倒角等特征易导致Fluent软件网格划分失败。因此为保证Fluent软件中网格划分的成功率，需对模型进行简化。在不影响仿真准确性的前提下，去掉一些微小零部件和倒角、圆孔等特征，得到简化模型如图1(a)所示。其中螺旋桨直径为∅177.8 mm，螺旋桨采用碳纤维材料；机架长610 mm，宽20 mm，高20 mm，机架采用铝合金材料；支撑环内径为∅420 mm，外径为∅440 mm，高度为10 mm，支撑环采用铝合金材料；动平台为正六边体，内切圆直径为∅180 mm，厚度为2 mm，动平台采用铝合金材料；电子舱直径为∅330 mm，电子舱采用丙烯腈-丁二烯-苯乙烯共聚物(ABS)材料；绳索设置为Line-Body单元，绳索材料为结构钢。在模型简化结束后，需为仿真模型设定合理的计算域，在保证计算结果接近真实情况的同时又使得计算量不至于过大。根据模型尺寸比例，采用空洞填充法在飞行型绳牵引并联机器人外围设置了一个半径为1 200 mm，高为2 500 mm的圆柱形计算域，作为系统的绕流流场，飞行型绳牵引并联机器人位于计算域的正中，如图1(b)所示。

图1 仿真模型与计算域模型建立Fig.1 Model building of simulation model and calculation area

2.2 网格划分与计算步骤

网格划分的质量直接关系到Fluent软件的仿真计算的准确性，是进行流体特性仿真计算的基础。本文对流体域和仿真模型分别采用特征抑制法进行单独的网格划分，采用混合网格进行划分，流体域用结构网格，仿真模型采用非结构网格，整个流体域以及模型共划分了197 411个网格。网格划分结果如图2所示。

将生成的网格文件导入Fluent软件求解器里进行求解，具体的求解步骤如下：

① 选择适用于飞行型绳牵引并联机器人可压缩流体仿真条件的基于密度型求解器。

② 湍流黏性模型采用Spalart-Allmaras单方程湍流模型，使用能量方程求解。

③ 流体设置为空气(文中视为理想气体)，密度为1.185 kg·m-3。在“黏性”一项中选Sutherland模型，采用三系数方法。

④ 类型为压力远场边界条件，壁面边界条件选择无滑移边界条件，壁面粗糙度为0.5 μm。湍流黏性比为10，坐标系设置为笛卡尔坐标系，大气压强设置为101 325 Pa，温度设置为300 K。

⑤ 方程设置为显式，流体和修正湍流黏性均选用二阶迎风格式。

⑥ 压力项松弛因子设置为0.8，密度、质量力项设置为1，动量项设置为0.5，湍动能项设置为0.6，耗散率项设置为0.6，湍流黏性项设置为0.6。

⑦ 流场初始化采用标准初始化方法，本文采用定常计算，总计算迭代步数设置为500步，收敛残差值设置为1×10-6(相对值)。

3 计算结果分析

3.1 计算收敛过程

根据四旋翼无人飞行器的实际飞行状况，设定飞行马赫数Ma为 0.05，攻角α=8°，其他参数保持不变，计算系统飞行过程中的气动参数，从而得到系统的升力系数曲线、阻力系数曲线和俯仰力矩系数曲线。计算此时的升力系数CL、阻力系数CD和俯仰力矩系数CM。CL、CD与CM均随迭代次数的增加而发生振荡，如图3～5所示。

图3为升力系数CL随迭代次数的变化曲线，迭代370步左右后，曲线逐渐趋于稳定；图4为阻力系数CD随迭代次数的变化曲线，迭代220步左右后，曲线逐渐趋于稳定；图5为俯仰力矩系数CM随迭代次数的变化曲线，迭代220步左右后，曲线逐渐趋于稳定。

图4 阻力系数随迭代次数的变化曲线Fig.4 Curve of the change of the drag coefficient with the iterative process

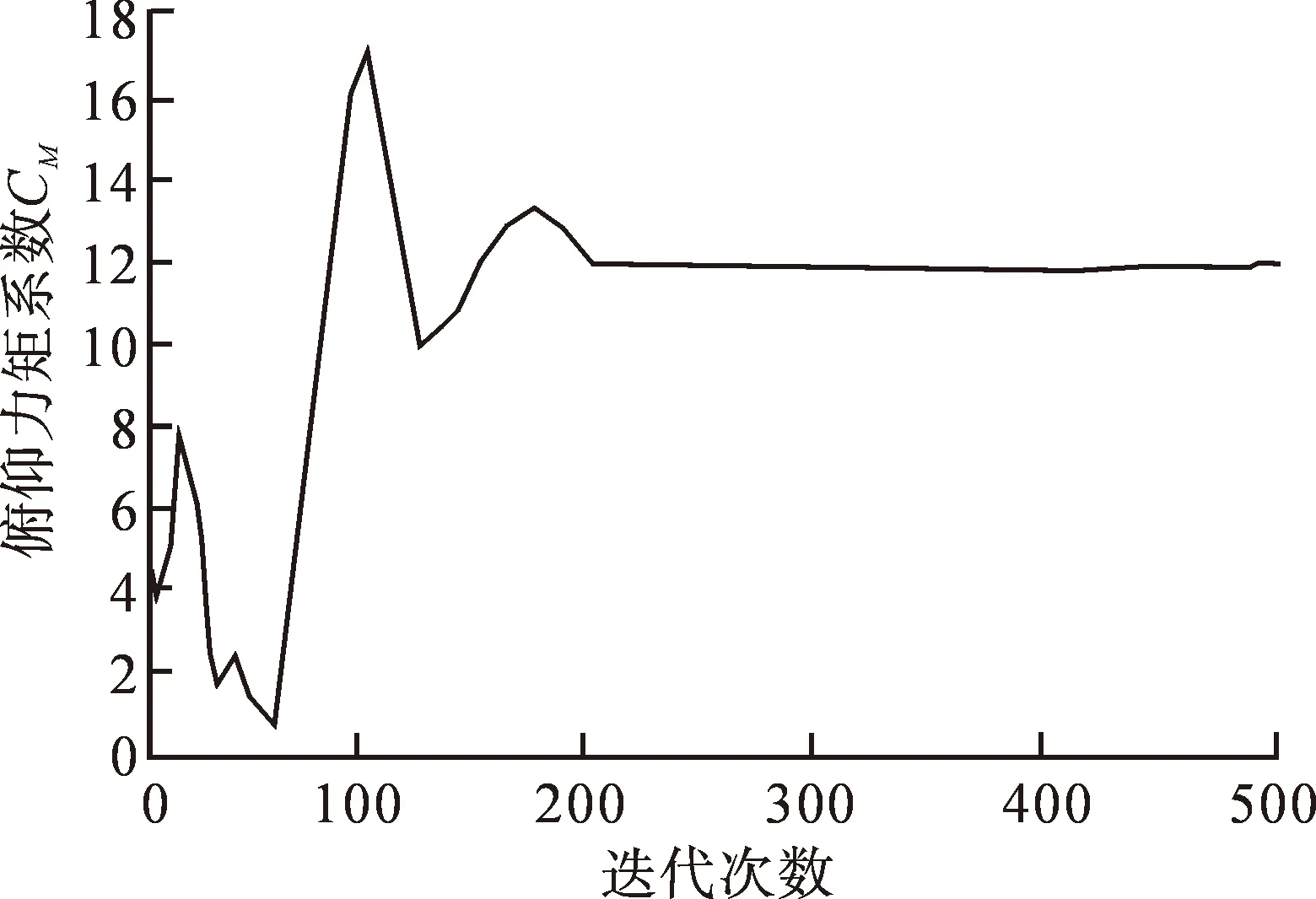
图5 俯仰力矩系数随迭代次数的变化曲线Fig.5 Curve of the change of the pitching moment coefficient with the iterative process

从图3～5可以看出，迭代次数达到500步后，曲线均稳定收敛，表明所设计的系统是稳定的，证明了气动布局设计的合理性。

3.2 不同速度与攻角对气动力因数的影响

为了进一步研究飞行速度及攻角对于飞行型绳牵引并联机器人气动力因数的影响，飞行型绳牵引并联机器人的飞行马赫数分别设定为0.05，0.10，0.15，通过改变攻角大小，计算以上三种飞行马赫数下的升力系数CL、阻力系数CD和俯仰力矩系数CM，结果如图6～8所示。

图6 不同马赫数下升力系数随攻角变化曲线Fig.6 Curve of the change of the lift coefficient with the attack angles at different Mach number

升力系数随攻角变化曲线，如图6所示。飞行马赫数为0.05和0.10时，升力系数随攻角增大而迅速增大。飞行马赫数为0.15时，变化较为复杂，攻角α∈[0°,8°]时，升力系数随攻角增大而增大；攻角α∈[8°,12°]时，升力系数基本保持不变；攻角α∈[12°,16°]时，升力系数随攻角增大而减小。因此当四旋翼无人飞行器速度较大时，攻角达到临界值后，升力系数保持不变甚至减小，旋翼上的气流被干扰，从而损失升力，气流从四个旋翼表面开始分离，引起侧滑，最终导致失速。因此当四旋翼无人飞行器速度较大时，仅在一定范围内可通过增大攻角的方法来提高升力，而攻角超过临界值后，升力保持不变甚至减小，造成四旋翼无人飞行器颤振甚至失稳坠落。

阻力系数随攻角变化曲线，如图7所示，总体来看阻力系数随攻角的增大而增大。飞行马赫数为0.05时，阻力系数随攻角的增大而缓慢增大；飞行马赫数为0.10，攻角α∈[0°,12°]时，阻力系数随攻角的增大而迅速增大；攻角α∈[12°,16°]时，阻力系数增速减缓，这符合亚声速阻力气动变化规律[2]。速度较小时，阻力系数明显偏小；速度较大时，阻力系数较大，但不同速度条件下的曲线之间的差异并不显著。这说明速度增大到一定程度以后，速度对阻力的影响将减小。

图7 不同马赫数下阻力系数随攻角变化曲线Fig.7 Curve of the change of the drag coefficient with the attack angles at different Mach number

俯仰力矩系数随攻角变化曲线，如图8所示。俯仰力矩系数既受攻角的影响，又受飞行速度的影响。飞行马赫数为0.05，攻角α∈[0°,12°]时，俯仰力矩系数随攻角增大而增大；攻角α∈[12°,16°]时，俯仰力矩系数反而随攻角的增大而减小，这说明低速大攻角使俯仰力矩系数降低[10]。飞行马赫数达到0.10时，俯仰力矩系数基本随攻角线性增大；飞行马赫数达到0.15时，俯仰力矩系数随攻角增大而增大，在攻角α∈[8°,16°]时增速变大。

图8 不同马赫数下俯仰力矩系数随攻角变化曲线Fig.8 Curve of the change of the pitching moment coefficient with the attack angles at different mach number

3.3 飞行型绳牵引并联机器人表面压力分布

飞行器表面压力分布是飞行器设计的重要性能指标，可真实反映飞行器的绕流特性。飞行马赫数为0.15时，竖直向上飞行的飞行型绳牵引并联机器人的表面压力分布云图，如图9所示。由图9可以看出飞行型绳牵引并联机器人压力分布均匀，因而表面黏性摩阻不会出现波动[11]。这表明飞行型绳牵引并联机器人的气动布局设计合理，飞行状态稳定。在飞行中压强最大的部位在旋翼、电子舱和支架的上表面，不同颜色表示不同压力的变化，从入口到出口压力呈依次递减状态，压强范围为-2 610～1 970 Pa，负号代表空气在该部位流入，正号代表该部位空气因飞行机器人的飞行而被挤开。这些分析和数据为实际飞行中改变飞行器攻角、旋翼翼面所受力矩提供了理论依据。

图9 飞行型绳牵引并联机器人 表面压力分布云图(Ma= 0.15)Fig.9 Surface pressure distribution nephogram of the flying cable-driven parallel robot (Ma= 0.15)

4 结 论

通过Fluent软件数值仿真计算，采用单方程湍流方程，分析了飞行型绳牵引并联机器人的气动特性，得到结论为

1) 在给定飞行速度时，升力系数、阻力系数和俯仰力矩系数曲线均具有收敛性以及表面压力分布的均匀性，说明飞行型绳牵引并联机器人结构稳定，气动布局设计合理。

2) 飞行速度较低时，升力系数随攻角增大呈正比增大；飞行速度较高，攻角为0°～8°时升力系数随攻角正比增大，攻角为8°～16°时，升力系数随攻角增大而减小。

3) 飞行速度较低时，阻力系数随攻角增大而缓慢增大；飞行速度较高时，阻力系数在攻角为0°～12°时正比增大；在攻角为8°～16°时，阻力系数缓慢增大。速度增大到一定值后，不同速度条件下的阻力系数差别不大。

4) 俯仰力矩系数既受到攻角的影响，又受飞行速度影响。飞行速度较大时，俯仰力矩系数随攻角增大而呈正比增大；飞行速度较低，攻角为8°～16°时，俯仰力矩系数随攻角增大而减小。

5) 飞行速度越大，气动特性参数不一定越大。要结合实际情况，进行具体分析。气动特性的仿真分析结果将为下一步的结构优化设计和运动控制提供理论依据。