基于多向波前法的岛屿孔洞修补

李 松 马聪聪 陆 帆 曹菁菁 周 勇

武汉理工大学物流工程学院，武汉，430063

0 引言

文物受自然环境、人为活动的影响，表面极易出现孔洞、残缺。为减少传统接触式修复方法对文物的二次破坏，人们采用三维扫描系统对文物模型进行数据采集，以指导后面的修复。受测量技术与精度的限制、文物自身形状与缺陷等因素的影响，被扫描物体的点云模型易出现孔洞。孔洞破坏了文物的完整性，对后续数据的处理也产生较大影响，因此，对模型孔洞进行修补是逆向工程中十分重要的环节。

针对网格模型孔洞的修补，研究人员进行了大量研究。PERNOT等[1]提出曲率最小化原则，在孔洞周边区域曲率最小化的前提下通过新增三角面修补孔洞。GIRSHICK等[2]采用非均匀有理B样条(NURBS)曲面生成补丁、修补孔洞。ARGUDO等[3]提出双谐波场的网格修补算法，可以较好地修补复杂孔洞和岛屿孔洞。谢倩茹等[4]采用波前法使孔洞区域不断缩小，根据曲率特征细分网格。刘云华等[5]基于区域生长的方法对尖锐特征丢失的孔洞进行修补，获得了较好的效果。晏海平等[6]通过建立径向基函数的隐式曲面完成孔洞修复。袁天然等[7]通过构建拉格朗日方程对复杂孔洞进行修补。张立国等[8]基于径向基函数对岛屿孔洞进行修补，提升修补速度。

对于岛屿孔洞的修补，上述方法均难以得到理想的修补效果：直接删除岛屿面片将其变为普通封闭孔洞会造成特征信息丢失；在曲面拟合过程中将岛屿三角面作为控制点会引起网格相交。为了有效实现岛屿孔洞的修补，本文提出一种基于改进波前法的多向波前法，以有效提升岛屿类孔洞的修补效果。

1 多向波前法概述

三角网格模型表面的孔洞可以分为封闭孔洞、半封闭孔洞和岛屿孔洞[9]。本文算法的实验模型为封闭的网格模型。封闭模型中不可能存在半封闭孔洞，因此下面仅对封闭孔洞与岛屿孔洞进行研究。

封闭孔洞是最常见的孔洞，其边界连接成一个封闭环。岛屿孔洞是指在一个较大孔洞内有少量孤立的三角面孔洞。将岛屿孔洞中范围最大的边界定义为孔洞边界，将孔洞边界内的三角面集合称为岛屿面片，将岛屿面片对应的边界定义为岛屿边界。图1为三角网格模型封闭孔洞与岛屿孔洞示意图。

图1 网格模型孔洞类型Fig.1 Hole type of grid model

孔洞修补就是从孔洞边界开始不断向孔洞区域插入离散点与三角面，从而使孔洞不断缩小。波前法可控性高、网格生成速度快[4]，是孔洞修补中常用的方法。该方法首先要检测孔洞边界，并以此作为初始波前，按照一定的规则在孔洞区域插入新增点与三角面片，每完成一次插入，孔洞边界就会发生变化，需调整波前，循环上述过程直至完成孔洞修补。

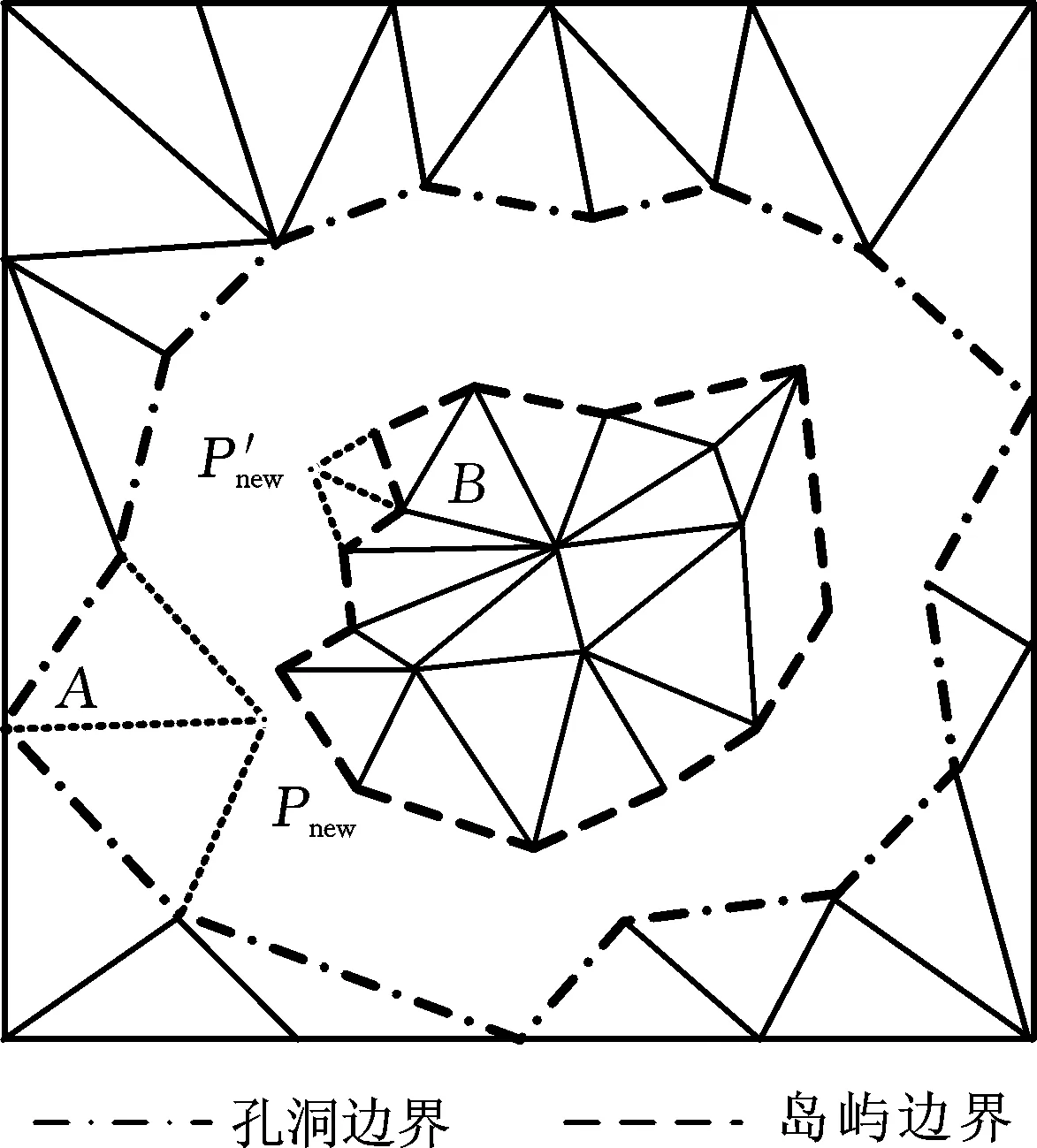
图2 多向波前法原理Fig.2 Principle of multi-directional advancing method

封闭孔洞与岛屿孔洞的区别在于波前的组成。传统波前法针对只有一条边界的孔洞。多向波前法原理如图2所示，将孔洞边界与岛屿边界同时作为初始波前，插入离散点。以波前与插入的离散点为基础，不断向孔洞区域内新增三角面，逐渐缩小孔洞区域。孔洞边界发生变化时，调整更新波前。重复上述过程直至修补结束。

2 算法详细步骤

2.1 孔洞边界识别

封闭的三角网格包含边界边与内部边。每条边都有邻接三角形，只有1个邻接三角形的为边界边，有2个邻接三角形的为内部边。边界识别原理如图3所示，遍历模型的所有边，找到边界边AB并令其为种子边，从种子边的2个顶点开始寻找邻接边，可以快速找到边界边。当边界边首尾相连、构成封闭的空间多边形ABCDEFGHIJK时，完成一个完整的孔洞边界搜索。

图3 边界边识别原理Fig.3 Principle of boundary recognition

对于岛屿孔洞，由于在大的孔洞内部存在岛屿面片，因此会搜索出多个边界，利用孔洞边界顶点、根据最小二乘法[10]拟合最小二乘平面，将孔洞边界投影到拟合的平面上，组成目标区域。将孔洞边界顶点的一阶邻域也投影到拟合的最小二乘平面上，若投影点位于目标区域内，则为岛屿边界，反之，则为孔洞边界。

2.2 孔洞边界预处理

孔洞边界边的长度相差较大，会影响离散点的插入，而且后续网格化的过程会产生狭长的三角面片，降低网格质量。因此在新增离散点之前，需要对孔洞边界进行预处理，使其均匀化。

计算所有孔洞边长度及其平均值lavg[11]，令阈值为1.5lavg，孔洞顶点以Vi(i=1，2，…)表示，当某条边ViVi+1的长度l>1.5lavg时，计算边ViVi+1的中点Vnew。删除原有孔洞边和对应邻接三角形，孔洞边更新为ViVnew和Vi+1Vnew，孔洞三角形更新为ViVnewVj以及VnewVi+1Vj。

2.3 离散点三角面插入

对岛屿孔洞进行修补时，岛屿面片的边界最小角θmin往往会大于180°，传统波前法并未对此进行考虑，会生成狭长三角面，降低网格质量。因此，本文对传统波前法中新增点插入规则进行改进，改进的插入规则如下：

(1)以孔洞边界和岛屿边界为初始波前。

(2)计算两两孔洞边的夹角，得到最小夹角∠Vi-1ViVi+1。

(3)将夹角最小的孔洞顶点作为初始填充位置，根据θmin的大小设置不同的顶点与三角面插入准则，具体准则如下：①0°<θmin<30°时(图4a)，θmin属于狭小角，直接连接两顶点会产生狭长的三角面单元，此时应合并该三角面，删除原有顶点Vi+1、Vi-1，计算Vi+1Vi-1的中点Vnew，如图4b所示，以Vnew为新顶点，重新建立三角面，如图4c所示。②30°<θmin<80°时(图5a)，直接连接点Vi-1、Vi+1，新增一个三角面。③80°<θmin<150°时(图5b)，在θmin的角平分线方向上，在孔洞边Vi-1Vi和ViVi+1边长的均值处添加新点Vnew，再连接Vi-1Vnew以及Vi+1Vnew，新增2个三角面。④150°<θmin<210°时(图5c)，在θmin的三等分线方向上，在孔洞边Vi-1Vi和ViVi+1边长的均值处添加新点Vnew1、Vnew2，连接Vi-1Vnew1、Vnew1Vnew2、Vi+1Vnew2，新增3个三角面。⑤210°<θmin<270°以及270°<θmin<360°时，按上述方式分别新增4个和5个三角面。

(4)按步骤(3)向孔洞区域内插入顶点与三角面后，更新波前。

(5)重复步骤(2)～步骤(4)，当边界内顶点数为3时，结束网格生长，完成孔洞修补。

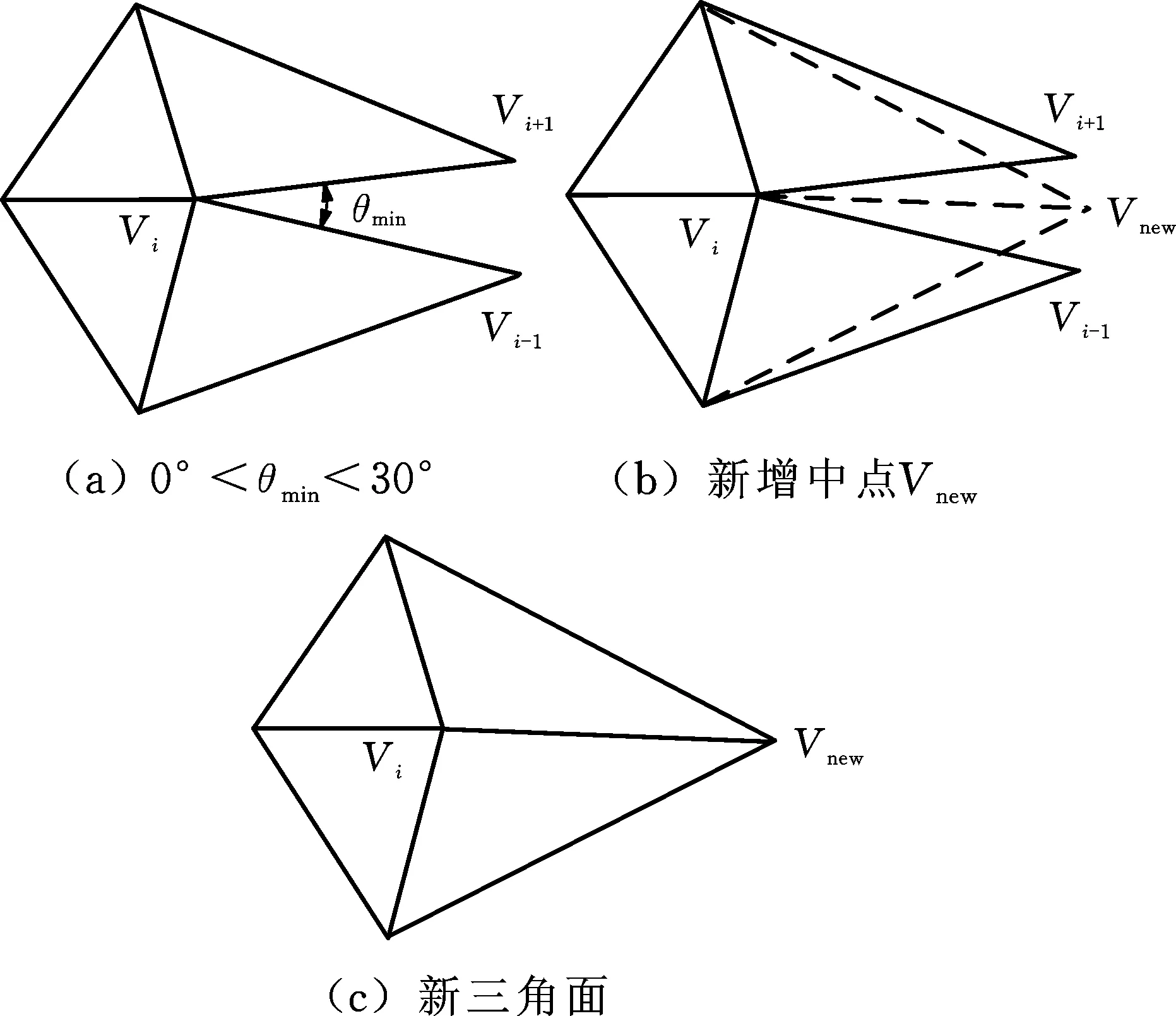
图4 夹角过小时剖分准则Fig.4 Split criterion under relatively small angle

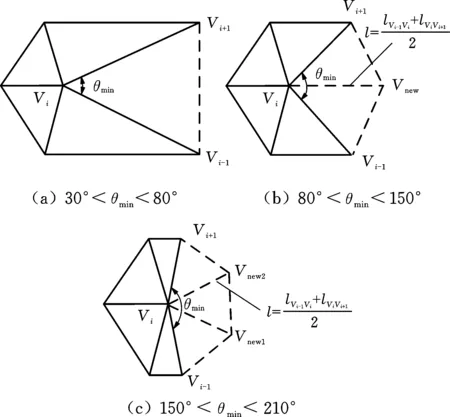
图5 最小角度原则新增点规则Fig.5 New point rule of minimum angle principle

2.4 新增顶点和新增面检验

使用波前法常会出现狭长三角形以及由不合理新增点引起的错误三角形，因此需要对新增顶点和新增三角面进行检验。

三维空间中的合理性检验比较复杂，可将空间三角形投影至二维平面完成检验。创建过点Vi且以n0=(n1+n2)/2(n1、n2为点Vi的两邻接三角形的法向量)为法矢的平面，将孔洞三角形投影至该平面，形成目标区域。若新增点的投影不在目标区域内，说明新增点出现在角平分线的反向延长线上，则该点为不合理点，应将其沿角平分线方向移动到顶点Vi的对称位置。

Delaunay三角剖分算法将三角网格中的最小角最大化，以预防狭长三角面的产生，提高网格质量[12]。平面Delaunay检验利用“空圆准则”即四点不共圆准则[13]，如果2个三角形不满足Delaunay准则，则根据“最大化最小角”原则将2个三角形的对角线进行交换，使其满足Delaunay准则，从而避免产生狭长三角形。

2.5 基于法矢与曲率的顶点调整

2.5.1法矢与曲率计算

为获得更好的曲面孔洞修补效果，利用顶点法矢和曲率调整新增顶点位置，使新增三角面最大程度地拟合孔洞原有表面特征。

三角网格模型顶点Vi的邻接三角形如图6所示，其中，Ni为Vi的单位法矢，fik为Vi的一个邻接三角面，Nik为fik的单位法矢，αk是fik在Vi处的顶角，ei,j和ei,j+1是顶角αk的2条边，gk为fik的质心，Gk为Vi到gk的距离。

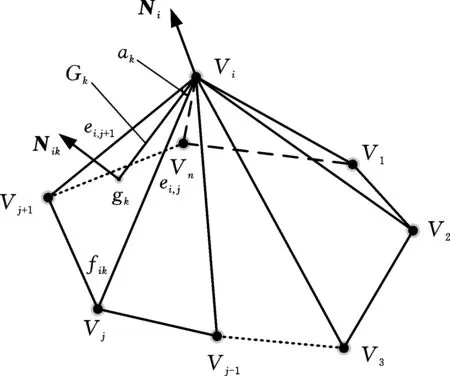
图6 顶点Vi的邻接三角形Fig.6 Adjacent triangles of vertex Vi

三角网格模型中某三角面片fik的单位法矢为

(1)

顶点法矢为该点所有邻接三角面片法矢的加权平均，若顶点有n个邻接三角面，令三角面fik的权重为wk，则顶点Vi的单位法矢为

(2)

权重wk由三角形形状因子λ和质心距Gk计算得到，λ的计算公式为

(3)

其中，a、b、c为三角形的边长。λ(0,1]，λ越大，三角形的规整程度越高[14]。λ与质心距Gk可以较好地评价三角形几何特性，将式(2)变形为

(4)

利用式(4)对点Vi的单位法矢进行计算，为了估算结果的准确性，在孔洞顶点的法矢计算之前，先将缺失部分补齐。

(5)

将新增点Vnew替换点Vj，点Vi处沿方向T的法曲率为

(6)

2.5.2顶点调整

由Vi指向新增点Vnew构成向量nnew，nnew的单位向量为nb，nb与顶点法矢Ni共同确定平面Π。将新增点在平面Π上进行调整，得到V′new，V′new与Vj组成的向量的单位向量为nB，如图7所示。

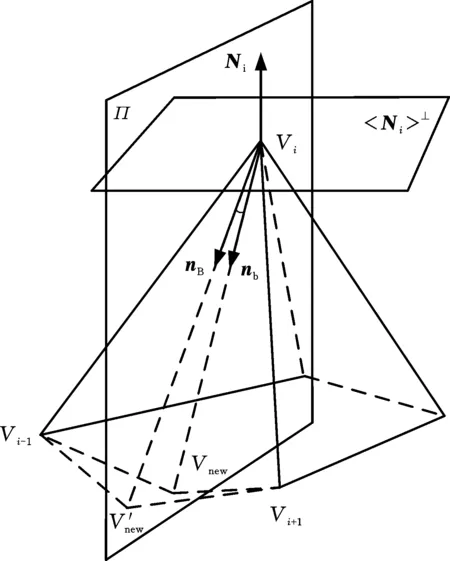
图7 新增顶点调整示意图Fig.7 New vertex adjustment diagrammatic sketch

若不进行顶点调整，则利用波前法求得新增点坐标：

Vnew=Vi+(|Vi-1Vi|+|ViVi+1|)nb/2

(7)

根据曲率ki(T)对顶点进行调整。ki(T)>0时，曲面在点Vi沿T方向处为凸，应将nb沿法向方向旋转θ角；ki(T)<0时，曲面在点Vi沿T方向处为凹，应将nb沿法向的反方向旋转θ角；ki(T)=0时，无需调整。联立式(4)、式(5)得调整角度θ以及nB：

(8)

θ=arccos(nB·nb)

(9)

调整后的坐标Vnew=Vi+(|Vi-1Vi|+|ViVi+1|)nB/2，将所有新增点按该过程完成调整。

本文算法在修补孔洞过程中基于波前法，以孔洞边界与岛屿边界为基础增加顶点与三角面，并基于法矢与曲率进行自适应调整，使新增区域尽可能拟合缺失部分的原有几何形状，使孔洞区域与非孔洞区域能光滑衔接，不断更新波前信息，有效减小修补痕迹。

3 实验结果分析

为验证本文方法的有效性，选择3组网格数据进行实验。实验环境为VS2013，采用OpenGL库验证算法。首先验证该算法对普通封闭孔洞的修补效果，采用带有孔洞的兔子模型进行实验。图8a所示模型的孔洞为狭长孔洞，利用文献[1]算法和文献[4]算法对其进行修补，得到的效果图分别为图8b、图8c，利用本文算法得到的结果如图8d所示，本文算法明显优于前两种算法。

手模型1中的孔洞为岛屿孔洞，图9a所示为孔洞模型，图9b为文献[1]算法的修补效果图，利用文献[4]算法得到的效果如图9c所示，本文算法对岛屿孔洞修补后的效果如图9d所示。对比发现，利用本文所提算法得到的新增面片与非孔洞区域过渡自然，保留了原有曲面特征，修补效果明显优于前两种算法。

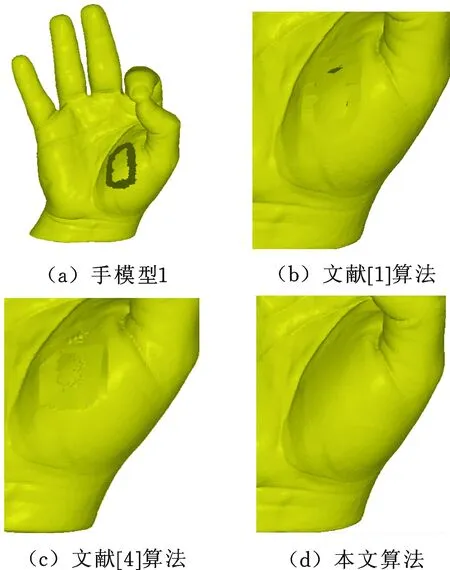
图9 手模型1孔洞不同算法修补效果Fig.9 Repair effect of different algorithms for Hand 1 model

手模型2孔洞的实验结果如图10所示，图10a所示为岛屿孔洞模型，可以看出该孔洞既包含大规模岛屿面片，也有较小的岛屿面片。利用文献[1]算法和文献[4]算法得到的修补效果分别如图10b、图10c所示。图10d所示为本文算法的修补结果，多向波前法在较大程度上保留了原有特征，过渡自然，无明显修补痕迹，效果较前两种算法更理想。

图10 手模型2孔洞不同算法修补效果Fig.10 Repair effect of different algorithms for Hand 2 model

采用形状因子定量评价修补效果，由2.5.1节可知，形状因子越接近于1，三角形面片越规整。表1所示为运用不同算法进行修补得到的新增三角网格平均形状因子，利用本文算法进行修补得到的平均因子超过0.85，在3种算法中效果最好，网格质量更高。

表1 新增网格平均形状因子

由上述3组实验可知，本文算法修补效果明显优于其他算法，采用本文所提多向波前法对青铜古剑模型(图11)进行修复。使用手持式三维扫描仪Artec Space Spider获得文物表面点云数据，对数据进行滤波、精简等预处理后，采用本文提出的多向波前法对孔洞进行修补。孔洞主要出现在剑柄与尾端部分，图12所示为剑柄部分孔洞修补前后的效果，剑尾部分孔洞修补前后的效果如图13所示，可以看出，利用本文算法进行孔洞修补后，文物表面能够与非孔洞区域自然过渡，很好地还原文物表面特征，并且较为复杂的岛屿与大范围孔洞也能得到较为理想的修补效果。

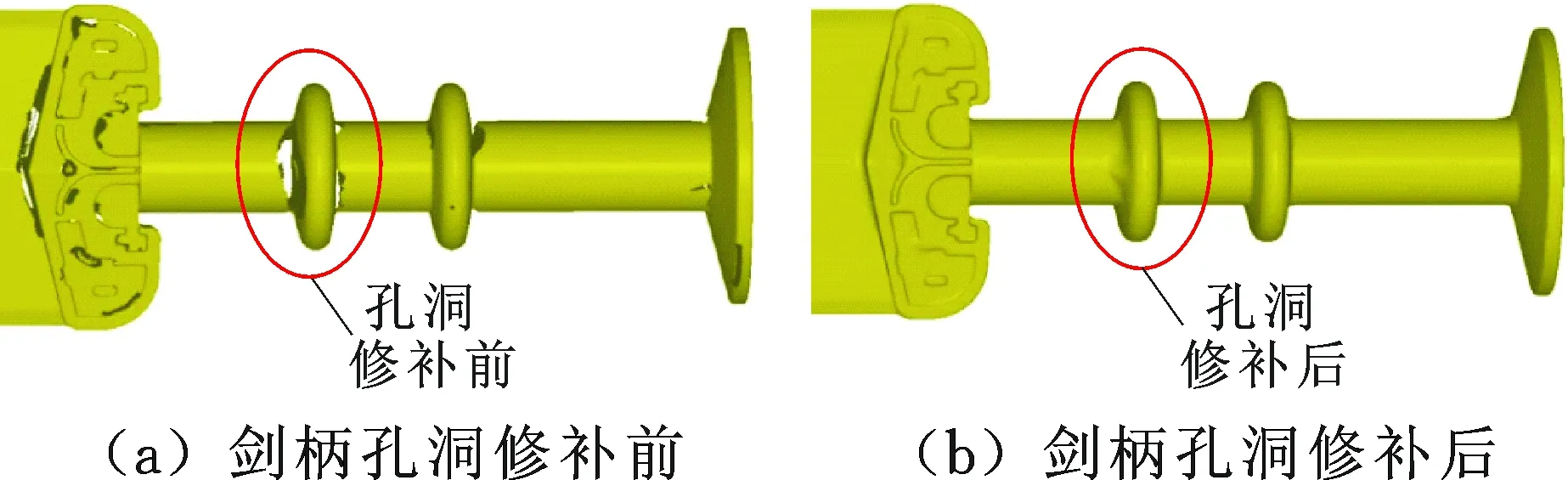
图12 剑柄部分孔洞修复前后对比Fig.12 Comparison of the sword hilt before and after repair

图13 剑尾部分孔洞修复前后对比Fig.13 Comparison of the sword tail before and after repair

使用联泰Lite600HD工业级3D打印机，采用光固化成形技术，以白色光敏树脂为材料，按1∶1的比例打印修补后的古剑模型，如图14所示。可以看到，经本文算法修补后进行打印的3D模型表面光滑，孔洞区域与非孔洞区域衔接光顺，也从侧面反映本文算法的优势。

图14 3D打印实物模型Fig.14 Physical model of 3D printing

4 结论

本文针对岛屿孔洞问题提出了多向波前法。首先识别孔洞边界并对其进行预处理，改进传统波前规则，完成离散点与三角面片的插入。对新增顶点与三角面片进行检验与优化，减少狭长三角面片。采用法矢与曲率信息完成对新增顶点的调整，使新增三角面最大程度地拟合原有表面特征，实现岛屿孔洞的修补。采用多组网格数据进行实验并对文物模型进行修复，结果表明本文算法生成网格质量较高，可以有效完成岛屿孔洞修补。孔洞修补算法的适用范围受原有模型的曲面复杂程度影响较大，当孔洞原有区域形状不规整、不均匀且孔洞部分过大时，利用孔洞修补算法难以得到理想的修补效果。对于曲面复杂度不同的孔洞，本文算法的适用范围将作为下一步的研究重点。