考虑结合面因素的模台振动系统动态特性

宜亚丽 向 健 刘 达 甄红卫 金贺荣

1. 燕山大学机械工程学院，秦皇岛，0660042. 北京星航机电装备有限公司，北京，100074

0 引言

预制混凝土(prefabricated concrete， PC)构件是实现建筑主体结构预制的基础，是实现住宅工业化的重要途径。作为预制混凝土生产线中重要工艺环节，混凝土预制构件振动密实过程中，混凝土振幅应满足极限幅值原则[1]，密实效果取决于密实过程中的参数选择。而作为振动密实制备的主要载体，模台振动系统的动态特性将直接决定混凝土预制构件制品的外形尺寸精度与力学性能，如何提高预制混凝土的振动密实性、均匀性是混凝土振动台的研究重点和难点。

徐平等[2]基于自同步理论建立双轴式惯性混凝土振动工作台的动力学模型，并对自同步条件进行分析，为提高振动工作台振动均匀性提供了参考。针对不同类型的混凝土，使用变频变幅电机可以实现较好的振动密实均匀性[3]，但经济性较差。贠志达[4]提出了基于混沌振动理论的宽频振动器设计方法，结合双质体弹簧振动系统，提高了振动密实性。韩彦军等[5]基于并联机构实现了中低频振捣，有效地提高了混凝土的振动密实性。机械结合面之间存在接触刚度、阻尼等动力学参数，研究结果表明，振动系统的机械结合面接触刚度占整个系统总刚度的60%～80%，结合面阻尼的占比更是高达90%以上[6]。目前的流水线生产模式无法避免引入非固定接触面，例如磁力和液压压紧装置的结合面，准确识别动力学参数是研究其动态特性的前提。BEMPORAD等[7]基于自仿射分形表面理论，采用边界元法对结合部动态特性分析并进行优化，使计算结果更为精确；POHRT等[8]引入结合面受力变形边界条件约束，解决结合面的切向和法向接触问题；FU等[9]基于粗糙表面接触分形理论建立了解析模型，分析了固定结合面的动态特性，并提出了修正参数；LI等[10]基于分形理论建立结合面法向与切向解析模型，讨论了摩擦与振动耦合作用下结合面的动态特性。结合面参数的整机理论有助于准确把握整机动态特性。汪博等[11]采用有限元法揭示结合面特性与机床主轴系统固有特性以及刀尖点频响函数之间的内在关系，为机床主轴系统动态特性研究及稳定性预估提供了参考；HUNG等[12-13]用弹簧单元模拟高速摩擦表面，研究了考虑结合面参数的转子动力学问题；姜彦翠等[14]考虑结合面和刀具因素，分析了不同工况参数对主轴系统固有频率以及刀尖频响特性的影响，研究成果有助于主轴系统工作稳定性提升工作的进一步展开；刘雪梅等[15]进行了有限元接触分析，研究结果表明考虑结合面参数会使机床主轴系统的振幅计算值增大；崔中等[16]建立了整机的三维有限元模型，利用反求方法确定了结合部的基础参数与刚度参数对整机模型低阶模态特性的影响。诸多考虑结合面因数影响的整机动态特性分析中的研究对象多为机床等精密装备，主旨在于提高整机的刚度，削弱振动对加工精密度的影响。模台振动系统通过振动实现混凝土密实，隔振弹簧的存在降低了整机刚度、增大了振幅，但是各振动子系统刚度均较高，引入结合面参数后将对各振动子系统的相对运动趋势产生较大影响，如何减小振动子系统邻近振幅差率，同时保证混凝土振幅满足极限幅值原则，从而提高预制构件外形尺寸精度，目前尚无此类相关研究，因此，需要将结合面作为影响参数，对具有非固定接触面的模台振动系统动态特性进行分析，从而为混凝土预制构件生产中合理工况参数的设定提供依据。

本文对具有不固定接触面的模台振动系统进行理论建模，基于Simulink分析结合面压力变化对各振动子系统振幅的影响，汇总36组面压下子系统相邻振幅差率；选取混凝土密实过程中子系统相邻振幅差率较小且混凝土振幅满足极限幅值原则的预制构件，进行外形尺寸测量与载荷试验。

1 模台振动系统z方向动力学建模分析

1.1 振动系统动力学建模

将结合面作为离散面，并建立弹簧阻尼单元，模台振动系统离散为四自由度串联振动系统，分别为模台振动设备、模台、模具以及混凝土，如图1所示，设备现场图片见图2。电机激振力为z方向，根据模台振动系统结构特点，建立图3所示的模台振动系统z向动力学模型，其中，M1为模台振动设备质量，M2为模台质量，M3为模具质量，M4为混凝土质量。

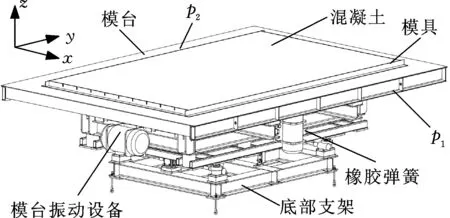
图1 模台振动系统结构示意图Fig.1 Schematic diagram of mold vibration system

图2 模台振动系统现场照片Fig.2 Scene photos of mold vibration system

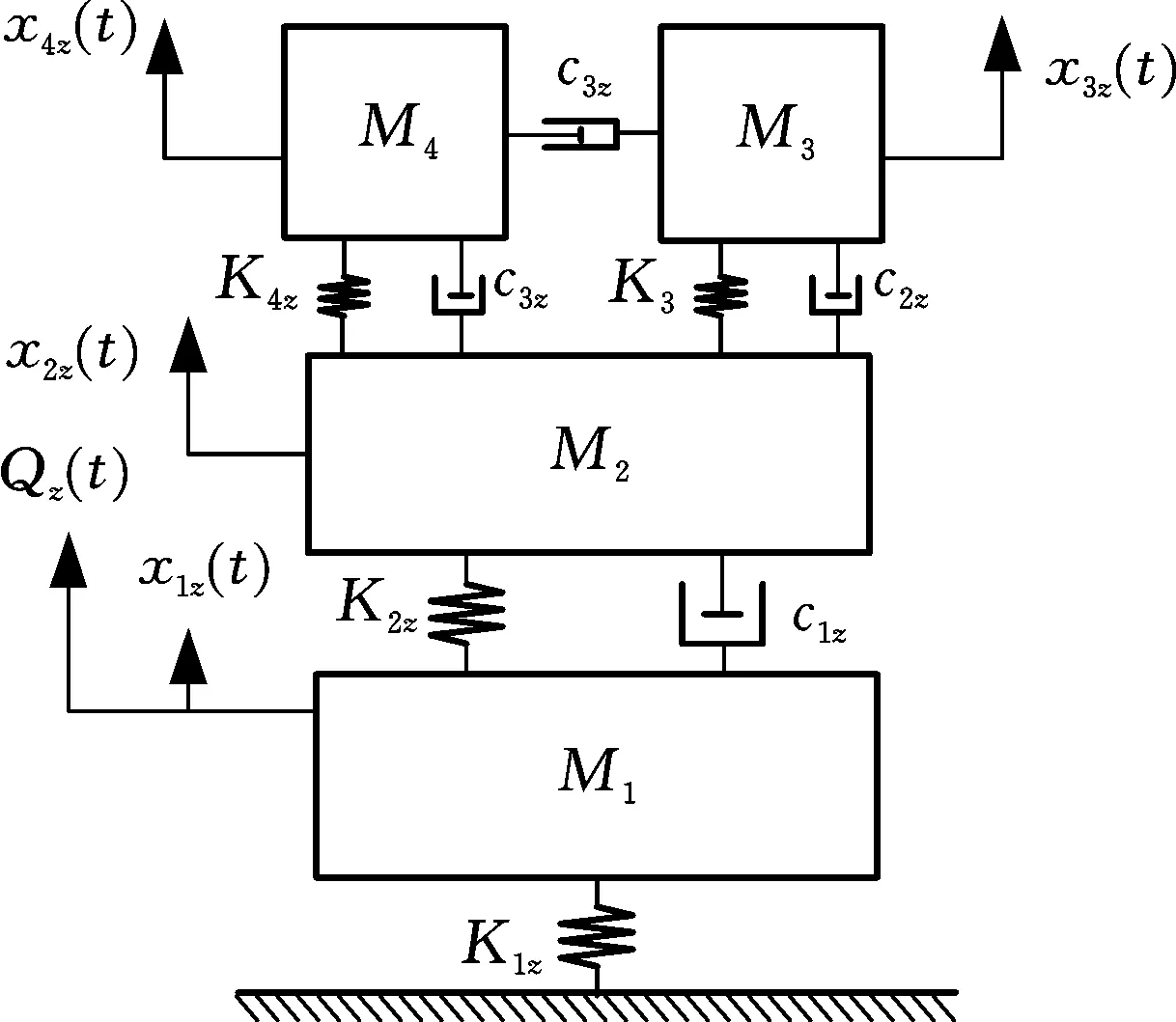
图3 模台振动系统z向动力学模型Fig.3 z-Axis dynamic model of mold vibration system

依据图3所示z向动力学模型，建立如下模台振动系统数学响应方程：

(1)

整理得

(2)

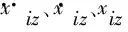
考虑模台振动系统在工作过程中较大的激振力以及各振动子系统的结构刚度，建立图4所示的子系统刚度关系。

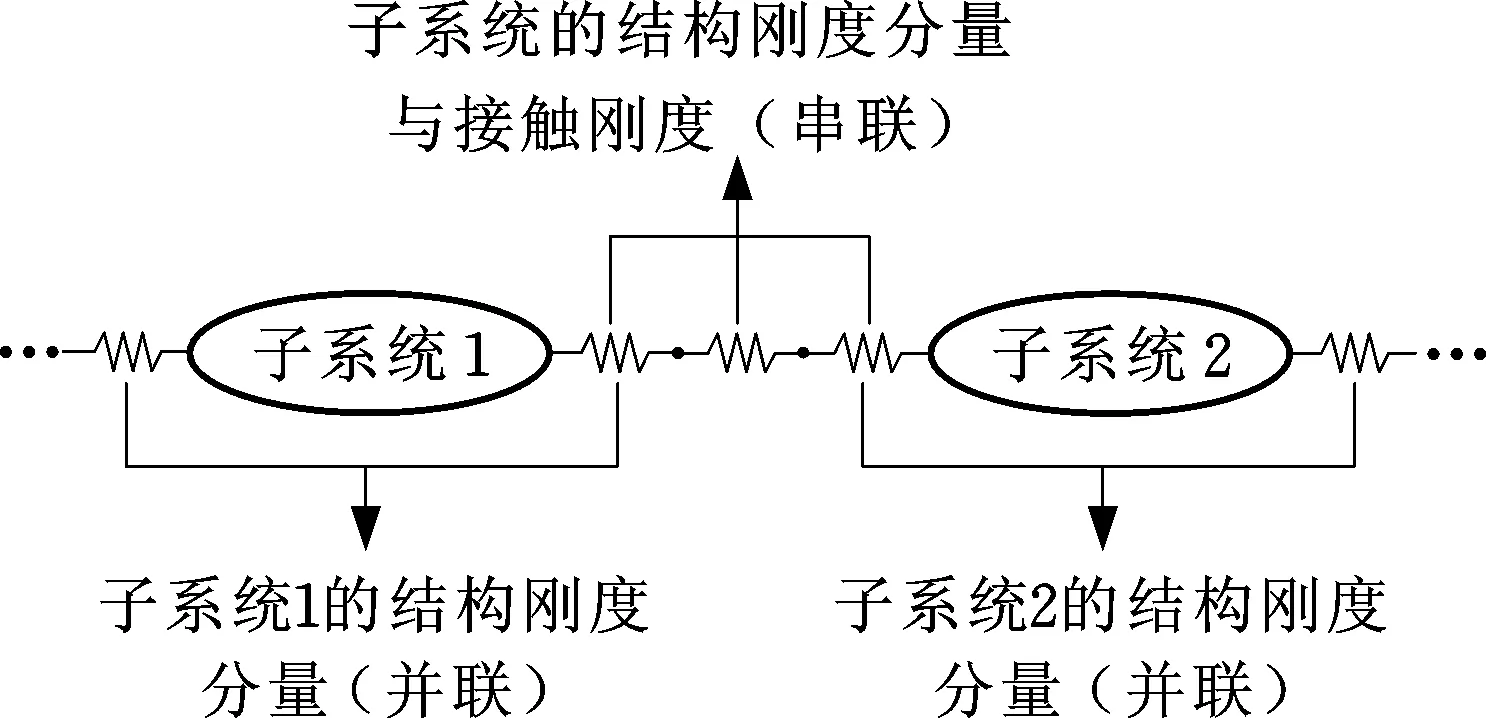
图4 子系统间刚度关系Fig.4 Subsystem stiffness relationship

任一子系统的结构刚度平均在其两侧并成并联关系，子系统之间均分后的结构刚度和结合面接触刚度为串联关系，建立以下关系方程：

(3)

(4)

(5)

(6)

式中，KSz为弹簧z向刚度；KMiz为各子系统z向结构刚度；K12z、K23z分别为模台与模台振动设备结合面、模具与模台结合面之间的法向接触刚度。

借用基于结合面法向阻尼耗能机理及MB接触分形修正数学模型，建立结合面法向接触阻尼数值解析模型和结合面间阻尼损耗因子模型[17]，从而对结合面接触刚度与阻尼K12z、K23z、c1z、c2z进行解析求解。

1.2 子系统结构刚度与阻尼参数求解

对各振动子系统三维模型简化并导入Workbench，依据实际装配方式在结合面处添加约束条件，在z向的假设均布外力F取值30 kN，计算得到最大变形量Smax，按下式计算结构刚度：

EI=∑F/Smax

(7)

模台z向变形云图见图5。根据式(7)计算结果整理得到子系统z向结构刚度，见表1。

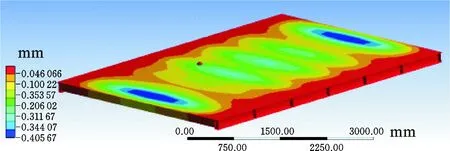
图5 模台z向变形云图Fig.5 Mold z-deformation map

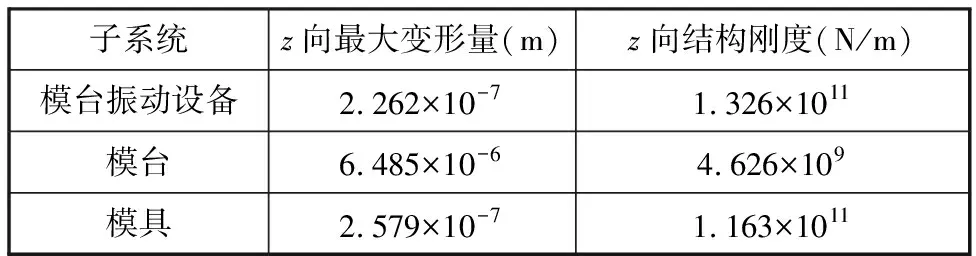
子系统z向最大变形量(m)z向结构刚度(N/m)模台振动设备2.262×10-71.326×1011模台6.485×10-64.626×109模具2.579×10-71.163×1011

在考虑结构阻尼时，将湿混凝土转化为各向同性的等效材料，对流体状态下混凝土的材料属性进行设定：泊松比μ取0.35，弹性模量E取5 MPa，密度ρ取1 700 kg/m3，阻尼比ζ取0.5，则混凝土z向结构刚度与结构阻尼计算公式如下：

K4z=AzE/hz

(8)

(9)

式中，Az为z向混凝土截面面积；hz为z向混凝土厚度。

联立式(8)、式(9)，可求得K4z=3.64×108N/m，c3x=1.48×105N·s/m，同理，也将橡胶弹簧转化为各向同性等效材料，求得KSz=1.78×107N/m。

1.3 基于Simulink求解系统位移响应

在本文所研究的模台振动系统中，存在模台与模台振动设备结合面(P1)、模具与模台结合面(P2)两个主要结合面(如图1所示)，结合面压力p1、p2取值范围为0.5～2 MPa，步长选取0.3 MPa，将36组结合面压力值代入结合面法向接触刚度与阻尼解析模型中，得到36组法向接触刚度K12z、K23z与接触阻尼c1z、c2z；将每组接触刚度计算值分别和已确定的各子系统z向结构刚度KMiz、橡胶弹簧z向刚度KSz代入式(3)～式(6)，可得到36组式(2)中各子系统之间的刚度Kiz(i=1，2，3，4)；将36组子系统之间的刚度、接触阻尼以及混凝土结构阻尼c3z分别代入式(2)，得到不同结合面压力下各子系统位移响应xiz随时间演变曲线，并提取稳态振幅。

分别将模台振动设备、模台、模具与混凝土创建成封装子系统，依据模台振动系统z向响应数学方程，创建Simulink连线框图，并利用Simulink子系统封装模块最终建立模台振动系统z向数值仿真模型，如图6所示。

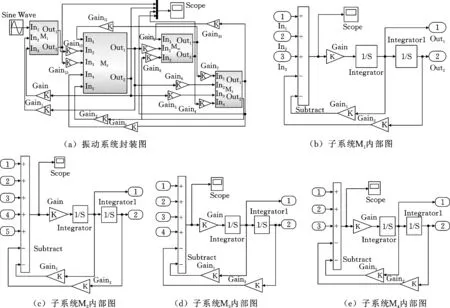
图6 模台振动系统Simulink仿真模型Fig.6 Simulink simulation model of mold vibration system

将每个子系统的非耦合项与耦合项分开，激振力为200 kN，振动频率为100 Hz，提取36组结合面压力下144个子系统位移响应幅值数据，绘制位移响应幅值规律曲线，如图7所示。

由图7可知，模台振动系统z向振动时，在结合面压力变化区间内存在振动子系统邻近振幅差率较小的状况，除了激振力和参振质量这两个影响因素外，结合面压力也影响混凝土振幅值，最大差值为0.023 mm。结合面压力较小，则结合面间接触刚度也较小，子系统邻近振幅差率较大；随着结合面压力增大，接触阻尼增大，激振力自下而上传递，子系统间的能量传递效率降低，阻碍了子系统间的相对运动，使得下部结构振幅偏大，上部结构振幅偏小，由此可知，适度的结合面接触刚度和阻尼关系能够降低子系统之间的振幅差。将子系统邻近振幅差率T定义为

T=(T1+T2/2)

(10)

式中，H1为模台振动设备振幅；H2为模台振幅；H3为模具振幅。

将依据模台振动系统响应方程求解的各振动子系统位移响应幅值代入式(10)，得到各振动子系统振幅差率，见表2。

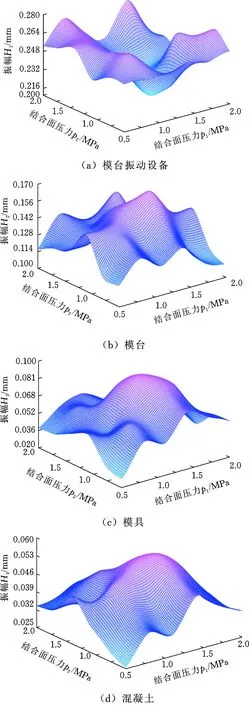
图7 模台振动子系统位移响应幅值随结合面压力变化曲线Fig.7 Change curve displacement response of mold vibration subsystem with pressure

振动子系统相邻振幅差率可评价混凝土振动密实性与均匀性，观察表2数据，子系统相邻振幅差率T最小值为0.341，此时两结合面压力p1、p2分别为1.4 MPa、1.1 MPa，可用于指导预制构件生产中的工况参数设定。

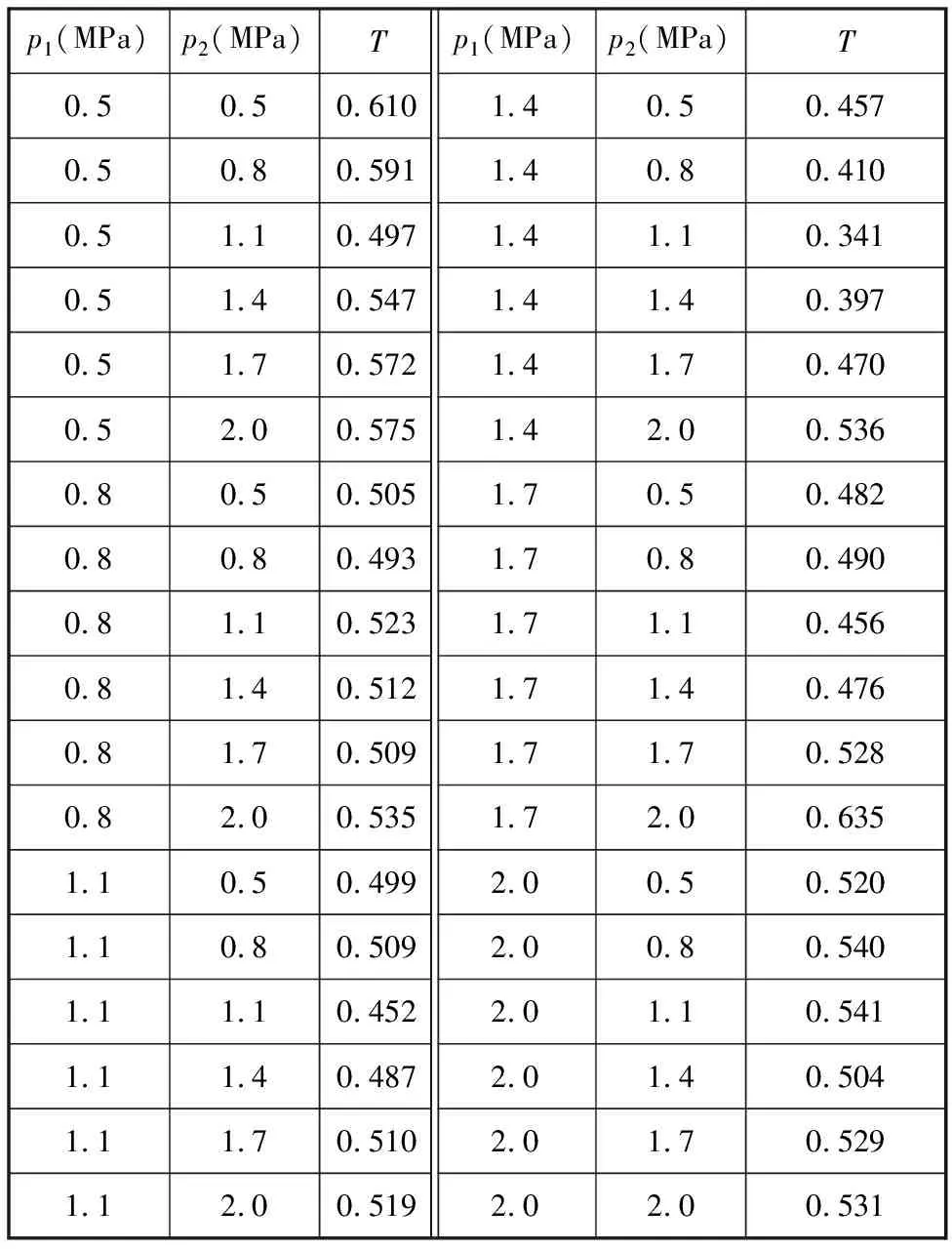
表2 子系统振幅差率T汇总表

2 模台振动系统有限元建模

2.1 结合面间有限元建模方法选取

虚设虚拟材料建模简单，分析效果较好，本文采用虚设虚拟材料来对振动系统进行有限元建模，虚拟材料与结合面两侧均采用bond约束，虚拟材料弹性模量、泊松比、厚度和密度的通用特性公式[18]如下：

E=E(E1,E2,μ1,μ2,Ra1,Ra2,P)

(11)

μ=μ(E1,E2,μ1,μ2,Ra1,Ra2,P)

(12)

h=h(h1,h2)

(13)

ρ=ρ(ρ1,ρ2,h1,h2)

(14)

式中，E1、E2分别为结合面1、2的弹性模量；μ1、μ2分别为结合面1、2的泊松比；Ra1、Ra2分别为结合面1、2的表面粗糙度；P为结合部所承受的法向载荷；h1、h2分别为结合面1、2的微观体厚度, 其值取1 mm为宜；ρ1、ρ2分别为结合面1、2的密度。

2.2 模台振动系统谐响应分析

以两结合面压力p1、p2分别为1.4 MPa、1.1 MPa为例求解子系统振幅值。在Workbench中将模型分解成有限个单元体，提取谐响应分析数据等同于计算任一子系统所有单元体的振幅均值，将结合面压力值代入式(11)～式(14)，结果添加到虚拟材料中，仿真完成后提取数据并绘制幅频特性曲线。

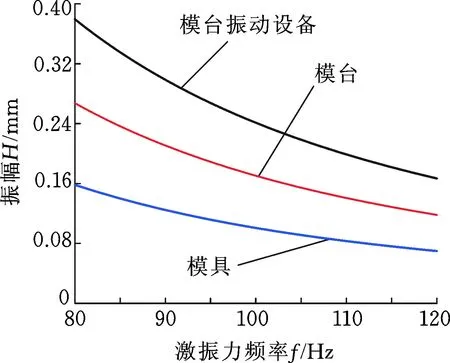
图8 子系统幅频特性曲线Fig.8 The amplitude-frequency characteristic curve of subsystem

提取激振频率为100 Hz时各子系统的振幅值，并与Simulink理论计算结果进行比较，求得误差率，见表3，其中理论计算结果见图7。

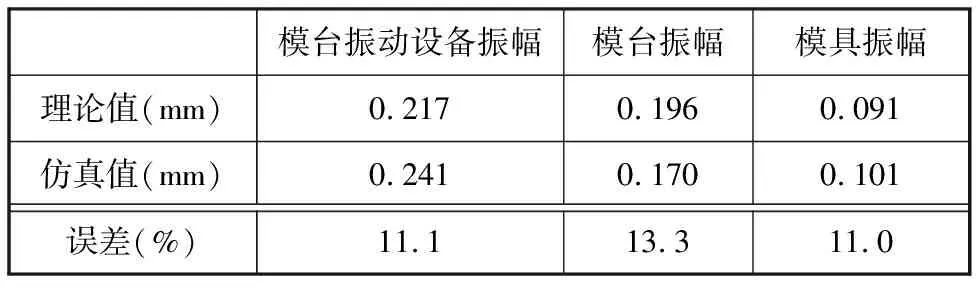
表3 理论计算结果与仿真结果对比表

表3给出了理论计算值与仿真值的对比，两者存在一定误差，最大误差为13.3%，分析误差产生的原因主要是:①在理论建模时没有考虑模台振动设备、模台和模具的结构阻尼；②单纯地研究了z向振动，并未考虑不同方向振动时的耦合性影响；③借用的结合面解析模型具有一定的误差；④电机与橡胶弹簧实际分布形式会对结果产生一定影响；⑤动力学建模时忽略了不同离散方式的误差；⑥理论计算时将结合部视为弹簧-阻尼器模型，而仿真时采用虚设虚拟材料来对结合面进行有限元建模。

3 预制构件外形尺寸测量与载荷实验

3.1 预制构件外形尺寸测量

前期实际生产时，预制构件的外形尺寸精度差，产品不合格率高。在流水线式模台振动系统中存在大量非固定接触面，结合面压力值均为经验取值，如施加的结合面压力不合适，极易造成相邻子系统振幅差值较大，从而影响预制构件制品尺寸精度，生产线前期运转时所生产的不合格预制构件如图9所示。

图9 不合格预制构件图Fig.9 Unqualified prefabricated concrete pictures

密实前，混凝土中的大量气泡会形成孔隙，从而降低预制构件制品的力学性能，因此，需要振动密实过程中尽可能清除混凝土中气泡，这就要求在振动密实时混凝土处于极限速度或极限幅值，低于该极限值将严重影响振动密实效果，4种不同振动频率下的最小速度、最小振幅和最小加速度值见表4。

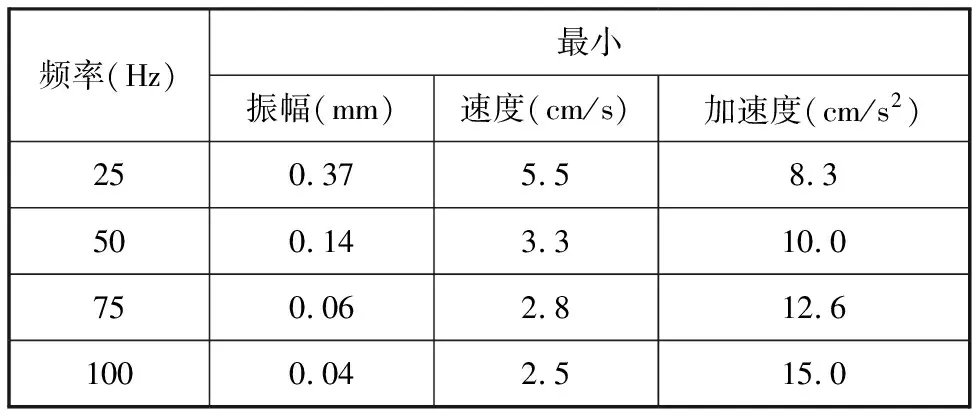
表4 最小速度、振幅与加速度值

基于振动子系统邻近振幅差率值较小同时混凝土的振幅符合极限幅值的参数选取原则，选定3组结合面压力作为工况参数(表5)，并进行预制构件生产制备，对制品外形几何尺寸进行测量，同时进行加载试验。

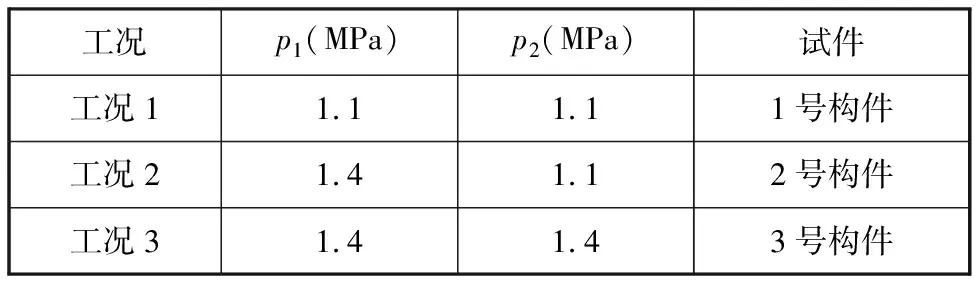
表5 三组工况

按照表5所示三种工况设置结合面压力值生产出的预制构件图片见图10。

图10 试验预制构件图片Fig.10 Testing prefabricated concrete images

按照行业对预制构件尺寸偏差测量规范要求，对3种不同工况下生产的试验预制构件进行尺寸偏差检验后的具体数值见表6。

表6 试验件尺寸偏差检验结果

Tab.6Testingresultsoftestingpiecesizedeviationmm

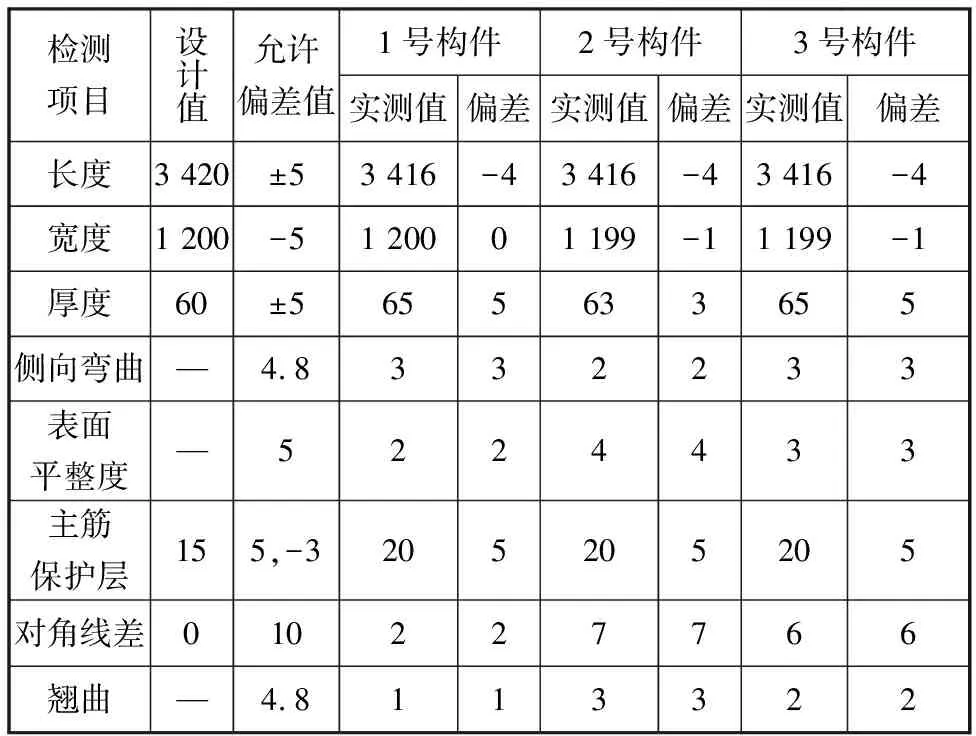
检测项目设计值允许偏差值1号构件2号构件3号构件实测值偏差实测值偏差实测值偏差长度3 420±53 416-43 416-43 416-4宽度1 200-51 20001 199-11 199-1厚度60±5655633655侧向弯曲—4.8332233表面平整度—5224433主筋保护层155,-3205205205对角线差010227766翘曲—4.8113322

由尺寸偏差检验结果可知，预制构件外廓尺寸精度较高，所有预制构件制品尺寸偏差均符合行业标准要求，振动子系统邻近振幅差率较小时，子系统间的相对运动趋势减弱，模具和模台间很难产生微小位移，振动平稳，生产出的预制构件外形尺寸满足使用要求。

3.2 板材载荷试验

在结构实验测试室的刚性台座上实施载荷加载试验，加载由一台500 kN液压千斤顶实现，载荷支撑由自平衡门式反力架提供，在被测试构件承载极限未知的情况下，采取小幅递增平稳加载的方式，至结构变形明显难以继续稳定施加为止。试验加载装置如图11所示，KCC-500型压力传感器布置在千斤顶下方，实现加载载荷测量与控制，对布置于试件上的钢梁如分配梁等进行提前称重记录，并附加在加载载荷内；布置6个位移传感器用于挠度测量，其中4个位移传感器用于测量支架沉降，2个位移传感器置于跨中，用于记录挠度结果含加载装置自重作用下的影响；沿底板混凝土表面纵向中心轴粘贴7个电阻应变片用于测量应变，使用TDS 303数据采集仪与上述载荷、位移、应变传感器连接，实现测试数据的显示和记录，试验现场照片如图12所示。

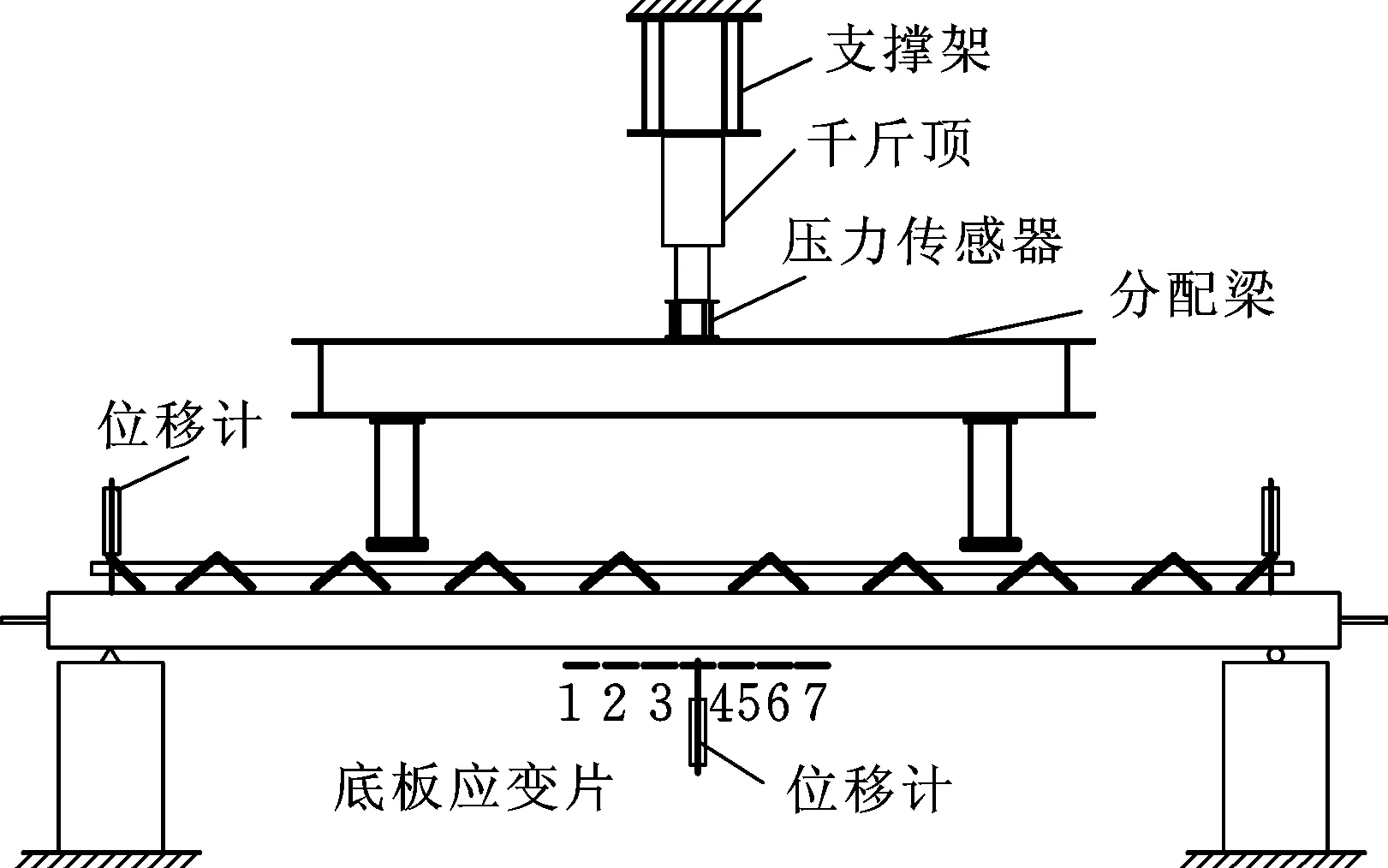
图11 试验装置示意图Fig.11 Schematic diagram of testing equipment

图12 试验图片Fig.12 Testing picture

载荷-挠度响应曲线可以直观、全面地表征结构刚度、承载力以及延伸性等结构性能，为方便对比分析，根据3块预制构件的试验数据绘制载荷-挠度曲线图，如图13所示，此处载荷加载不计预制构件自重。

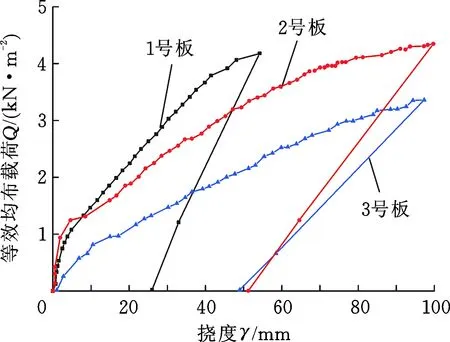
图13 预制混凝土构件底板载荷-挠度曲线Fig.13 The load-deflection curve of prefabricated concrete

本文所制备的混凝土预制构件强度等级为C40，根据《混凝土结构设计规范》(GB 50010—2010)，该等级混凝土结构的承载设计值不小于1.91 kN/m2，制备的3块试验预制构件达到最大挠度时的最小承载力为3.34 kN/m2，均大于承载设计值，符合验收指标；规范中要求挠度不小于45.53 mm，加载试验过程中1号构件的最大挠度值较小，挠度为54.36 mm时构件断裂，3块试验预制构件挠度极限值全部满足《混凝土结构工程施工质量验收规范》(GB 50204—2011)中关于极限挠度的验收要求。同时由于3块预制构件在制备过程中，振动密实时的激振力频率和结合面压力均有差异，导致其载荷-挠度曲线存在一定的差异。

混凝土的开裂与其应变紧密关联，当裂缝穿越应变片时，会使得应变激增且快速断裂失效，进而确定混凝土构件的开裂载荷。

在加载试验过程中，一般会在被测预制构件的跨中首先显现破坏迹象，之后是载荷施加位置，沿混凝土构件底板纵向中心轴线上布置多个应变片，用以测量尽可能接近于构件初始开裂时刻的开裂载荷值，并由此绘制出载荷-应变曲线，如图14所示。

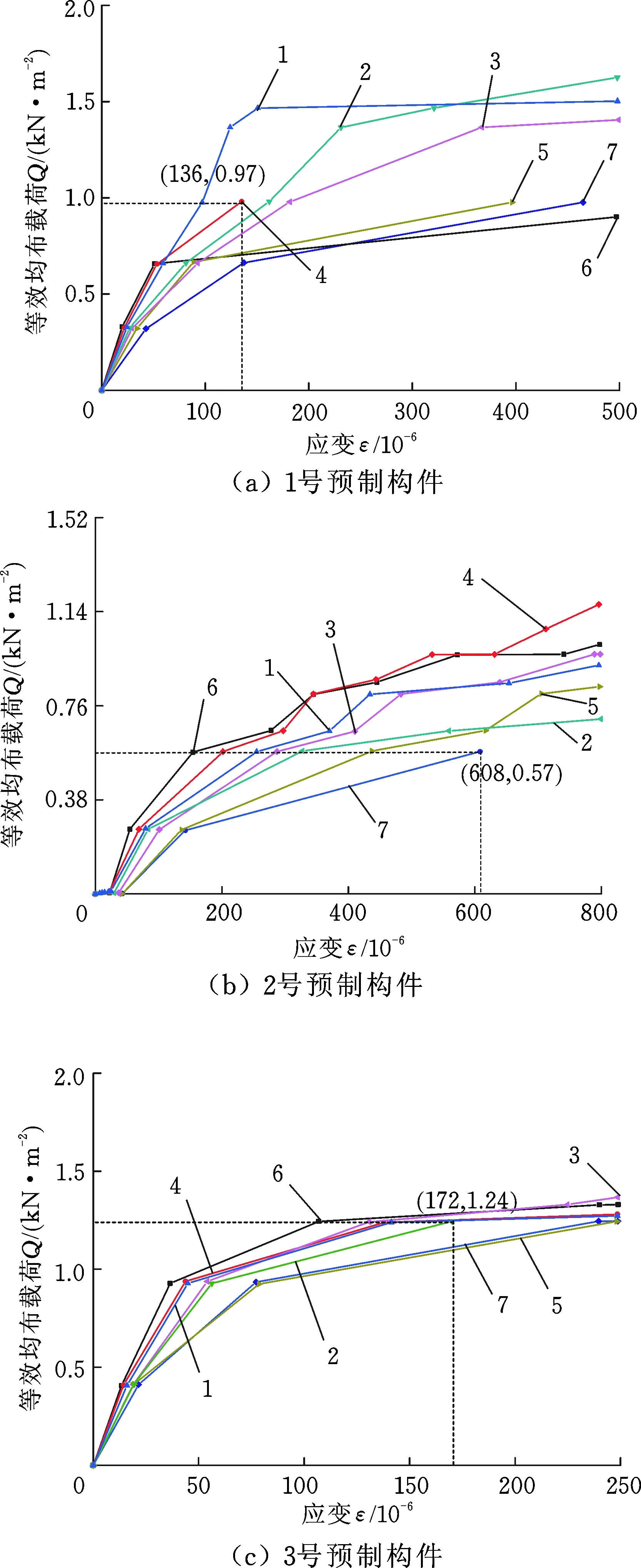
图14 预制构件底板载荷-应变曲线前段Fig.14 The before paragraph load-strain curve of prefabricated concrete

在相同载荷作用下跨中两侧的应变差值较小，表明混凝土构件的内应力分布均匀性较好；当加载载荷增到一定值后，混凝土构件显现出塑性形变特征，归其主因是其内应力增加呈现非线性；根据《混凝土结构设计规范》(GB 50010—2010)，强度等级为C40的混凝土预制构件抗裂检验系数许用值为1.25，3构件中2号构件的开裂载荷值最小，为0.57 kN/m2，实测抗裂检验系数值为1.39，大于许用值，由此判定3块试验构件开裂载荷均满足设计规范要求。

由试验测试结果可知，通过调节结合面压力能够降低振动子系统邻近振幅差率，在振动子系统振幅差率较小工况下所生产的预制构件的力学性能符合国家标准，即在此工况参数下的振动密实均匀性较好，能满足生产要求。综上，预制构件性能参数见表7。

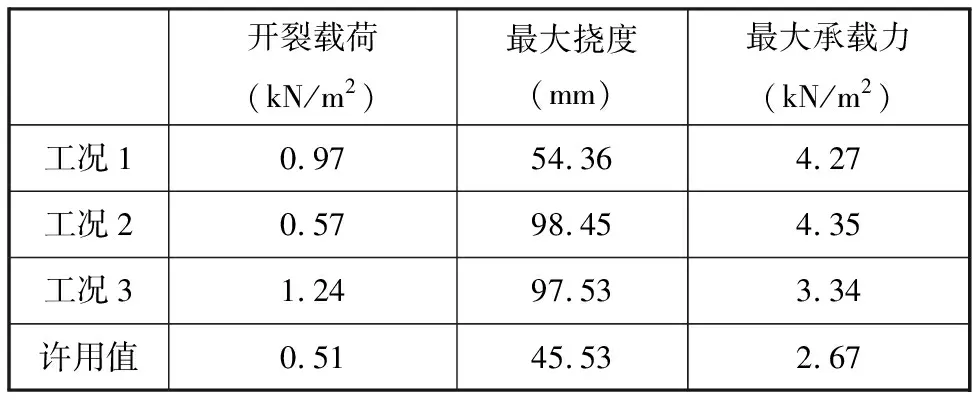
表7 预制构件性能参数

4 结论

(1)适中的结合面间接触刚度与阻尼关系可以降低子系统之间的振幅差率。

(2)验证了引入结合面参数会改变各振动子系统间的相对运动趋势，振动子系统的理论响应幅值与仿真结果的最大误差为13.3%。

(3)所制备的混凝土预制构件的外廓尺寸和承载能力均达到国标设计使用标准，进一步说明了减小振动子系统邻近振幅差率可以提高模台振动系统的振动均匀性，该工况下的振动密实效果能够满足实际工程使用需求。