基于A*算法和人工势场法的移动机器人路径规划
王洪斌 郝 策 张 平 张明泉 尹鹏衡 张永顺
1.燕山大学工业计算机控制工程河北省重点实验室,秦皇岛,0660042.燕山大学国家冷轧带钢装备及工艺工程技术研究中心,秦皇岛,066004
0 引言
近年来,移动机器人的路径规划问题成为研究热点,其主要思路是[1]根据能耗、路程、时间等性能指标,保证在存在障碍物的环境下,规划出一条从初始位置到目标位置的最优路径。在以往的研究中,根据环境信息的完全已知、部分未知或者完全未知等不同特点,通常把移动机器人的路径规划分为两部分:全局路径规划[2-3]和局部路径规划[4-5]。
环境建模和路径搜索是全局路径规划研究中的两个重要问题。在研究环境建模时主要应用可视图法[6]、拓扑法和栅格法。栅格法[7]是由栅格构成一个连通图,依据障碍物的分布,用搜索算法(A*算法[8]、遗传算法[9]、粒子群算法[10]、蚁群算法[11]等)生成从初始节点到目标节点的最优路径。粒子群算法[12]利用较小种群模式,通过单向信息流机制搜索最优路径。文献[13]融合了最大最小蚁群算法与蚁群系统算法的信息素更新方式,设计了与环境模型相符合的适应度函数,实现了路径规划。但上述算法数据复杂,计算量大,很难快速规划出一条平滑的最优路径。作为一种典型的启发式搜索算法,A*算法能够遍历所有可达节点,再根据估价函数来搜索较优路径。文献[14]提出跳点搜索策略,减少了遍历过程中所需访问的节点数,运行速度很快,但路径中仍存在转折点。由于移动机器人自身存在非完整约束,在转折点处不能连续运动,为了解决路径平滑问题,文献[15]引入多项式曲线实现平滑路径的生成,但存在曲率峰值过大问题。文献[16-17]分别提出改进的三阶Bezier曲线和改进Pseudo-Dubins曲线方法,这两种方法均能实现路径平滑,但算法的过程繁琐,效率低。
规划机器人的运动路径时,若存在结果不可行的情况,一般会在全局规划后进一步采用局部路径规划的算法,这种方法能够有效提高系统的实时性。目前,主要应用模糊逻辑算法、遗传算法和人工势场法等方法来进行局部路径规划。其中,人工势场法结构较为简单,易于实现实时控制等优点,但该算法存在局部极小值问题。针对上述缺点,文献[18-20]分别提出了建立多行为体系结构、添加虚拟水流法和增设虚拟中间目标点方法来解决局部极小值问题。但是针对上述方法的研究中,并没有综合考虑路径长度、路径安全性、转弯角度等因素来对路径进行处理,因此,由这种算法得出的路径综合适应性不高。
在动态复杂的未知环境中,传统的路径规划方法很难达到最优路径指标,因此,本文提出了一种将全局路径规划与局部路径规划相结合的混合路径规划算法。在该算法中,需要首先完成全局路径规划,然后在全局路径的基础上利用二次A*搜索和动态切点调整法优化已规划路径,最后根据环境信息的变化状况,在全局路径规划的结果上,采用基于自适应步长调节方法的人工势场法进行局部优化。该混合方法不但能根据已知的环境信息规划出全局最优路径,同时能在局部变化的环境中实现实时避障和动态目标追踪,较好地克服了传统算法复杂、计算量大、效率不高等问题。
本文以3自由度非完整轮式移动机器人作为研究对象,相比2自由度机器人,移动机器人不能实现全向移动,转折点处不能连续直线运动,需要转动一定角度调整姿态,对路径规划有了更多的限制,例如路径中存在的转折点个数以及转动角度等,因此,研究非完整移动机器人的路径规划意义重大。
1 A*全局路径规划算法
1.1 环境模型描述
机器人的环境模型是对其进行控制的基础,为了有效地描述机器人所处环境,将被控目标看作在二维平台上移动的点状物体,于是目标的运动轨迹可以为栅格地图上的黑色块,而可行区域则由白色块表示。环境M由栅格Mij构成:
M={Mij,Mij=0,1,2,3}
其中,Mij=0表示移动机器人的起始位置单元栅格;Mij=1表示无障碍区域单元栅格;Mij=2表示障碍区域单元栅格;Mij=3表示目标所处位置。
栅格大小的选取对于整个路径规划是很重要的,栅格选取较大,计算量就会减少,但得到的路径长度可能会增大;相反,栅格选取太小,路径规划的准确度就会提高,但规划过程缓慢。栅格大小主要由实验环境确定。栅格长度
其中,r为障碍物半径,R为机器人半径,δ为设定的安全距离。综上所述,可以将移动机器人的路径规划问题概述为通过在已得到的环境模型中的无障碍区域搜索,得到一条由栅格组成的连续的最短路径。
1.2 A*全局路径规划算法
A*算法[21]是一类搜索算法,它根据所定义的估价函数大小来确定最优路径。代价函数表示为
f(n)=g(n)+h(n)
(1)
其中,n为当前节点;f(n)为节点n的估价函数;g(n)为从起始点到当前节点n的实际代价值;h(n)为当前节点n到目标点的估计代价值。一般来说h(n)为欧氏距离,其定义如下:
其中,(xn,yn)表示当前位置处栅格的中心坐标;(xgoal,ygoal)则表示目标栅格的中心。通过优化可以得到当前位置到目标位置的最短路径。
传统A*算法能够有效地对目标进行全局路径规划,但其优化后得到的路径冗余点较多,且该方法得到的运动路线折线多、转折次数多、转折角度大,这些缺陷严重影响了路径规划的效果。本文根据传统A*算法的原理,进一步提出了一种新型A*算法。该算法利用二次A*搜索优化了目标路径的长度,这种方法能够仅保留路径中的起点、转折点和终点。对于存在非完整约束的移动机器人,其特性造成移动机器人不能在路径中的转折处进行直线运动,需要不断转动来调整自身的运动姿态,从而引起目标运动的角速度以及向心加速度发生变化。对此,本文提出了动态切点调整算法对路径进行平滑处理。
1.2.1路径点序列优化
在实现路径优化过程中,为了缩短路径长度,引入二次A*搜索算法。首先,将式(1)得到的估价函数作为初始值,并选取扩展点,扩展点的选择方法是选取与路径节点不相邻的后续路径点;进一步,以代价函数大小和是否穿过障碍作为判断依据,来确定上述两个节点之间是否存在新的路径。判断标准是,如果满足代价函数小于初始值、无障碍物这两个条件,则两点之间构成新的路径,并剔除中间节点,否则,路径为原有路径。最后,所生成的路径为最短路径,仅包含起点、转折点和目标点。
对两种A*算法在栅格地图为10 m×10 m的情况下进行仿真对比,结果如图1、图2和表1所示。
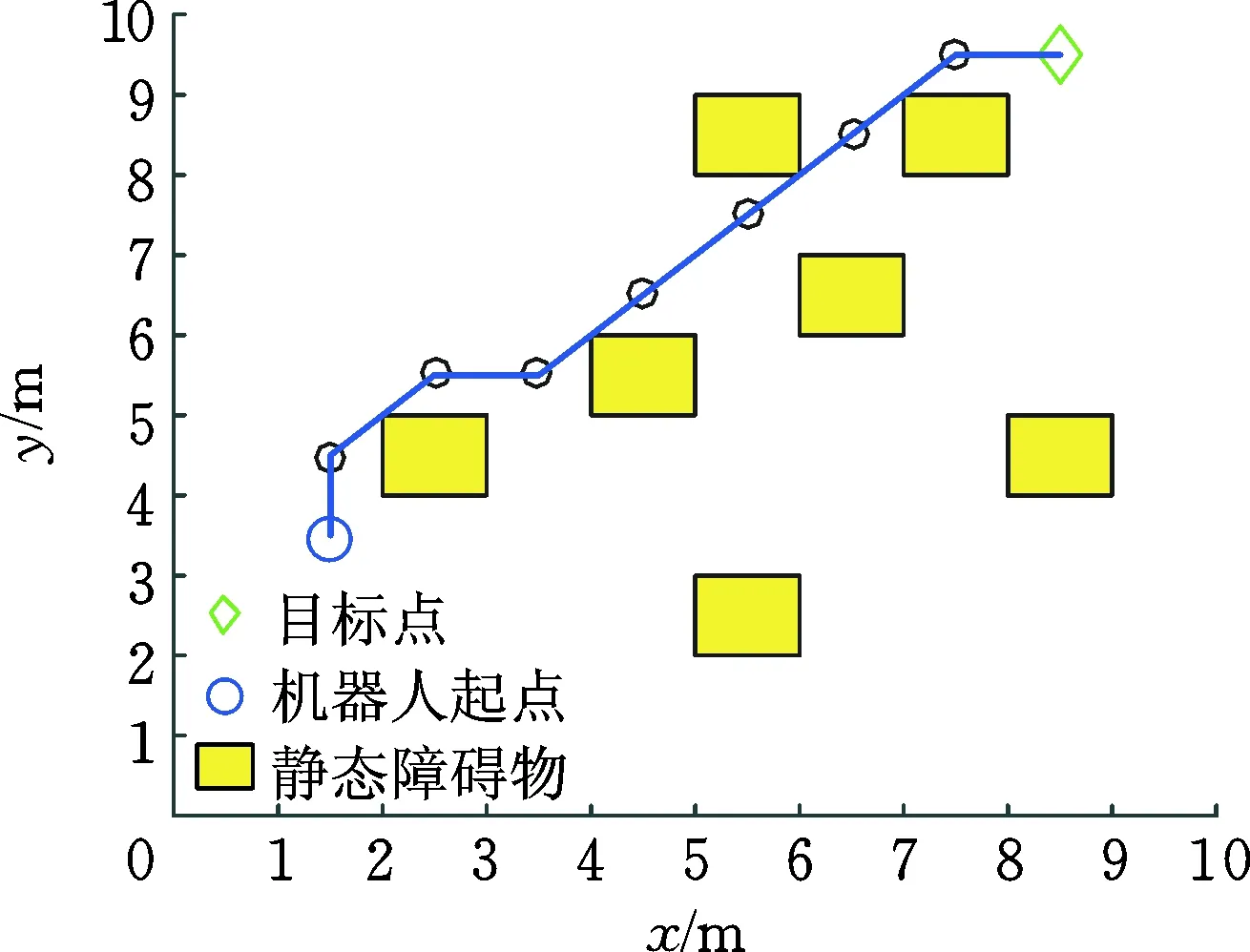
图1 一次A*算法寻优Fig.1 Linear A* algorithm optimization
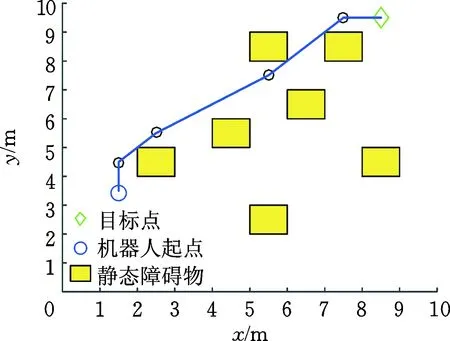
图2 二次A*算法寻优Fig.2 Twice A* algorithm optimization
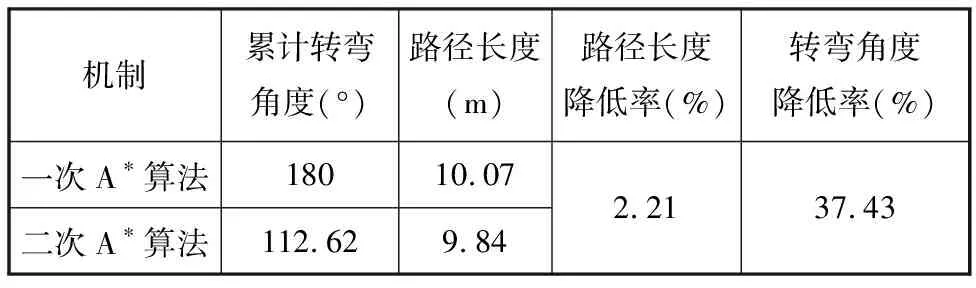
机制累计转弯角度(°)路径长度(m)路径长度降低率(%)转弯角度降低率(%)一次A∗算法18010.07二次A∗算法112.629.842.2137.43
比较图1、图2和表1的仿真数据可知,二次A*算法有效剔除了冗余点和折线,减小了规划路径长度,有效减少了转弯角度,实现了路径优化。
1.2.2路径平滑处理
二次A*算法可以规划出一条由线段组成的完整路径,而平滑的路径更便于移动机器人的控制。本文利用动态切点调整算法去除凹凸点,该方法能够得到既有曲率连续性,同时满足几何特性的路径。路径平滑示意图见图3。
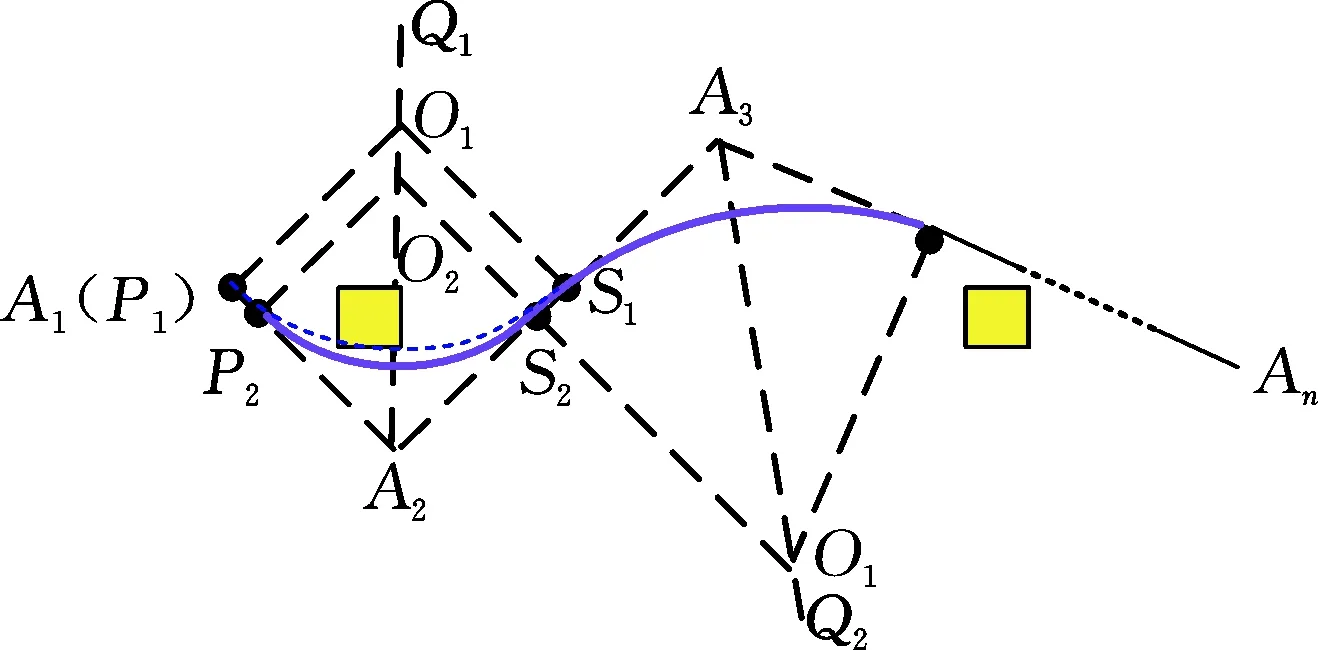
图3 路径平滑示意图Fig.3 Schematic diagram of the path smooth
机器人的初始位置为A1(x1,y1),终点位置为An(xn,yn)。从初始位置开始,依次对Ai(xi,yi)(i=2,3,…,n-1)转折点进行平滑处理。图3中,单调地使用固定切点会使机器人陷入包含障碍物的死区,因此,本文将固定切点改为动态切点,提出了动态切点调整算法,具体步骤如下:
(1)比较Ai-1Ai和AiAi+1两线段长度,选择较短边的端点P(xp,yp)为初始切点,过点P作垂线,与∠Ai-1AiAi+1(i=2,3,…,n-1)的角平分线AiQi-1相交于点Oi-1(x0,y0):
x0=(xp+k01yp+k01(k0x2-y2))/(1+k0k01)
(2)
y0=k0(x0-x2)+y2
(3)
相切圆的半径R可表示为
(4)
相切圆方程为
(x-x0)2+(y-y0)2=R2
(5)
式中,k01为较短边斜率;k0为角平分线斜率。
(2)判断相切圆是否与长边之间有交点S,如果有,则转至步骤(3);否则,转至步骤(4)。
(3)判断圆弧PS上是否存在障碍物,如果存在,则转至步骤(4);否则,用圆弧PS替代Ai-1AiAi+1,并转至步骤(5);
(4)切点P(xp,yp)沿着所在线段移动到P2(xp2,yp2),xp2可表示为
xp2=xp+λ|x2-xp|λ∈(0,1)
(6)
其中,λ依据实际情况设置。同时将P2设置为初始切点,并返回步骤(1)。
(5)判断此步骤确定的路径是否已经在环境模型中遍历所有的路径节点,若是,则返回步骤(1),否则结束。
2 改进人工势场局部路径规划算法
在机器人的移动运行过程中,能够通过机器人机身携带的传感器完成对所处局部环境变化的感知,根据实时检测的障碍物或目标的变化情况,采用人工势场法做出行为决策,及时避开障碍物,实现目标跟踪。
人工势场[22]由斥力势场和引力势场组成。在复杂的工作环境中,环境信息不断变化,为了进一步满足当前路径规划的需求,不能仅仅考虑机器人、目标位置和障碍三者之间的相对位置关系。为此,本文将机器人、目标与障碍三者间的相对速度关系作为优化路径的指标。引力势场函数Uatt可定义为
Uatt(q)=[mρ2(q,qg)+kv1ρ2(V,Vg)]/2
(7)
相应的引力Fatt可表示为
Fatt(q)=mρ(q,qg)+kv1ρ(V,Vg)
(8)
式中,m、kv1为引力场正常量;ρ(q,qg)为机器人与目标点之间的欧氏距离;ρ(V,Vg)为机器人和目标点之间的相对速度。
斥力势场函数Urep可定义为
(9)
Urepv=kv2ρ2(V,Vobs)/2
(10)
(11)
相应斥力Frep可表示为
(12)
Frepv=kv2ρ(V,Vobs)
(13)
(14)
其中,k、kv2为斥力场正常量;ρ(q,qobs)表示机器人与障碍物两点之间的欧氏距离;ρ(V,Vobs)表示机器人和动态障碍物之间的相对速度;ρ0为常数,表示障碍物对机器人产生作用的最大范围;α为障碍物的相对移动方向和移动机器人与障碍物连线的夹角,当α∈(-π/2,π/2)时,障碍物的移动方向确定为靠近移动机器人。
2.1 虚拟子目标的增设
移动机器人在行进过程中,存在一种严重影响运行的局部最小值陷阱,即障碍物和目标点对移动机器人产生的排斥力和吸引力相等时,使得移动机器人不能顺利抵达目标点。因此,本文提出增设虚拟子目标法。借助虚拟外力,使机器人摆脱陷阱,成功抵达目标点。具体方法如下。
(1)首先依据移动机器人的状态信息判断是否进入局部最小值陷阱,以连续五个步长作为判断依据,当总的移动距离小于βL(L为步长,β∈[2,4])时,改变β,移动机器人可以提前检测到自身陷入局部极小值陷阱。
(2)程序跳转到虚拟子目标增设模块,存储使移动机器人陷入局部最小值陷阱的障碍物位置信息,形成障碍物群,充分考虑目标点位置与障碍物群位置信息,判断障碍物在移动机器人与目标点连接线左右两端数目多少,选择障碍物群左侧或右侧为目标障碍物,然后利用下式得到虚拟子目标位置:
(15)
式中,(xob,yob)为目标障碍物位置;(xg,yg)为原目标所处位置;(x,y)为机器人的当前位置;β1,β2为可调参数,β1,β2>0。
移动机器人摆脱上述陷阱后,将撤出虚拟子目标,移动机器人不再受外力作用。移动机器人将在原目标和障碍物的合力作用下向原目标点靠近。
2.2 自适应步长调节
通过控制步长的变化,能够使搜索更加灵活。在障碍物较少的情况下,增大步长可以降低机器人调整位姿的频率,缩短运动时间。但是步长不能随意改变,盲目增大步长会增加碰撞的概率。为此,本文使用自适应步长调节的方法来减少碰撞的概率。
这种算法需要选择补偿,主要考虑环境的复杂度以及机器人与目标的相对距离。机器人机身携带的传感器,能够探测到周围障碍物数目以及障碍物与机器人自身的位置关系,由此判断环境的复杂程度。本文设立的判定标准如下:当机器人探测到的障碍物数目大于设定值或机器人探测到障碍物与自身相对位置小于设定值时,环境即为复杂环境。在这种情况下,机器人步长取Lmin;而当机器人离目标很近时,为避免出现步长太大而超过目标,或者步长太小而无法跟踪目标的情况,步长取Lmid;当机器人处于简单环境时,步长取Lmax。这样既节省运行时间,还能优化路径。
采用改进的人工势场法有效避免了传统人工势场法中目标不可达、易陷入局部极小值等问题,在动静态障碍物干扰下,实现对动态目标的快速跟踪。
3 仿真与分析
利用MATLAB仿真软件对本文算法进行仿真,并与传统算法进行仿真对比。
3.1 静态障碍物+静态目标
采用新型A*全局路径规划算法和基于三次B样条函数的A*算法在栅格地图为10 m×10 m的情况下进行仿真,结果如图4、图5所示,其中系数λ=0.1。
由图4、图5可以发现,利用两种算法均可实现规划一条起点至终点的平滑路径。由图5中的局部路径放大图可以看出,A*算法与三次B样条函数法的路径规划算法在处理路径平滑过程中,单独使用三次B样条函数会导致移动机器人陷入障碍物死区,并与障碍物发生碰撞,而本文提出的改进的A*全局路径规划算法在处理转折点时,采用动态切点调整方法,因此可以规划出平滑、安全的最优路径。
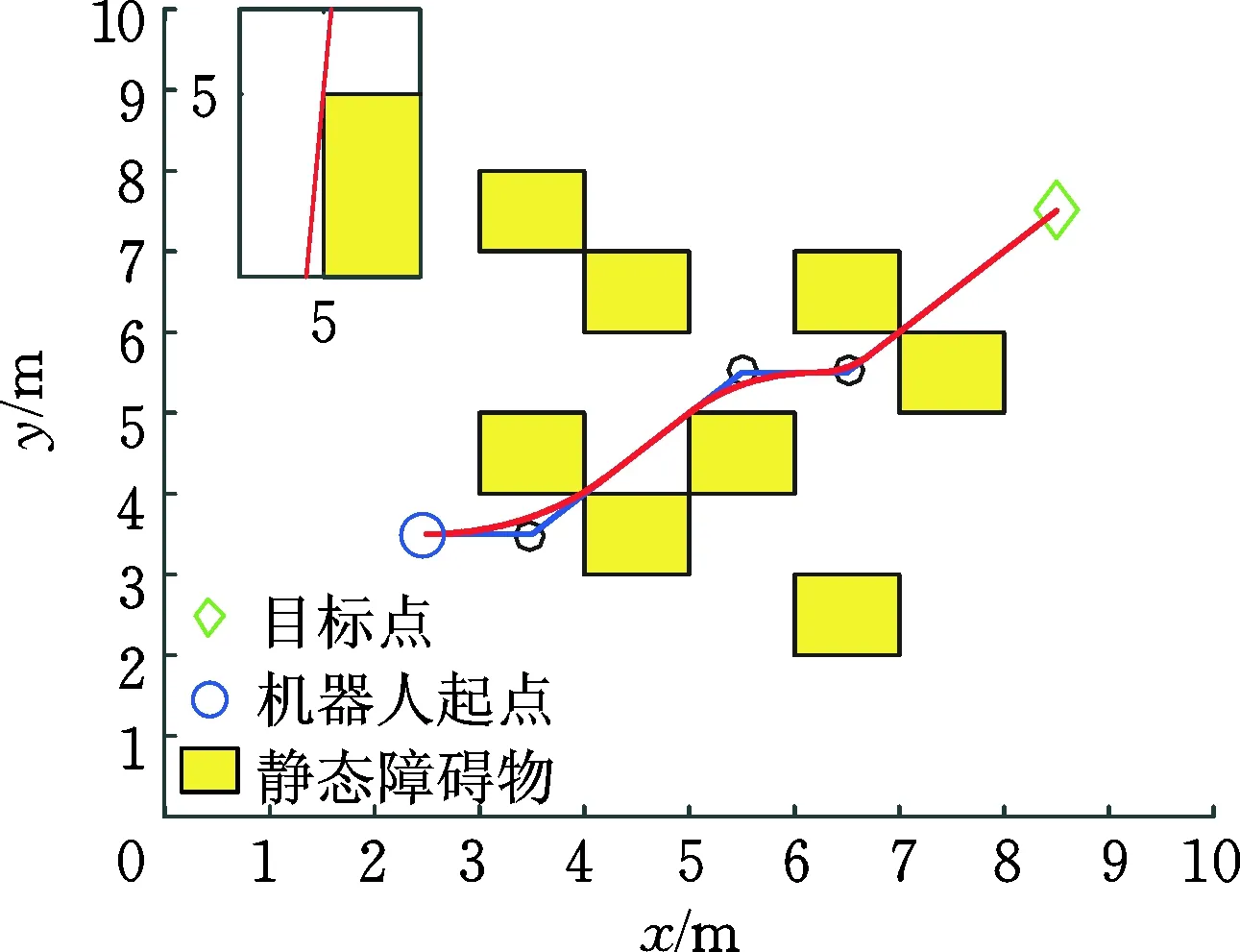
图4 改进的A*算法的路径规划Fig.4 Path planning for improved A* algorithm
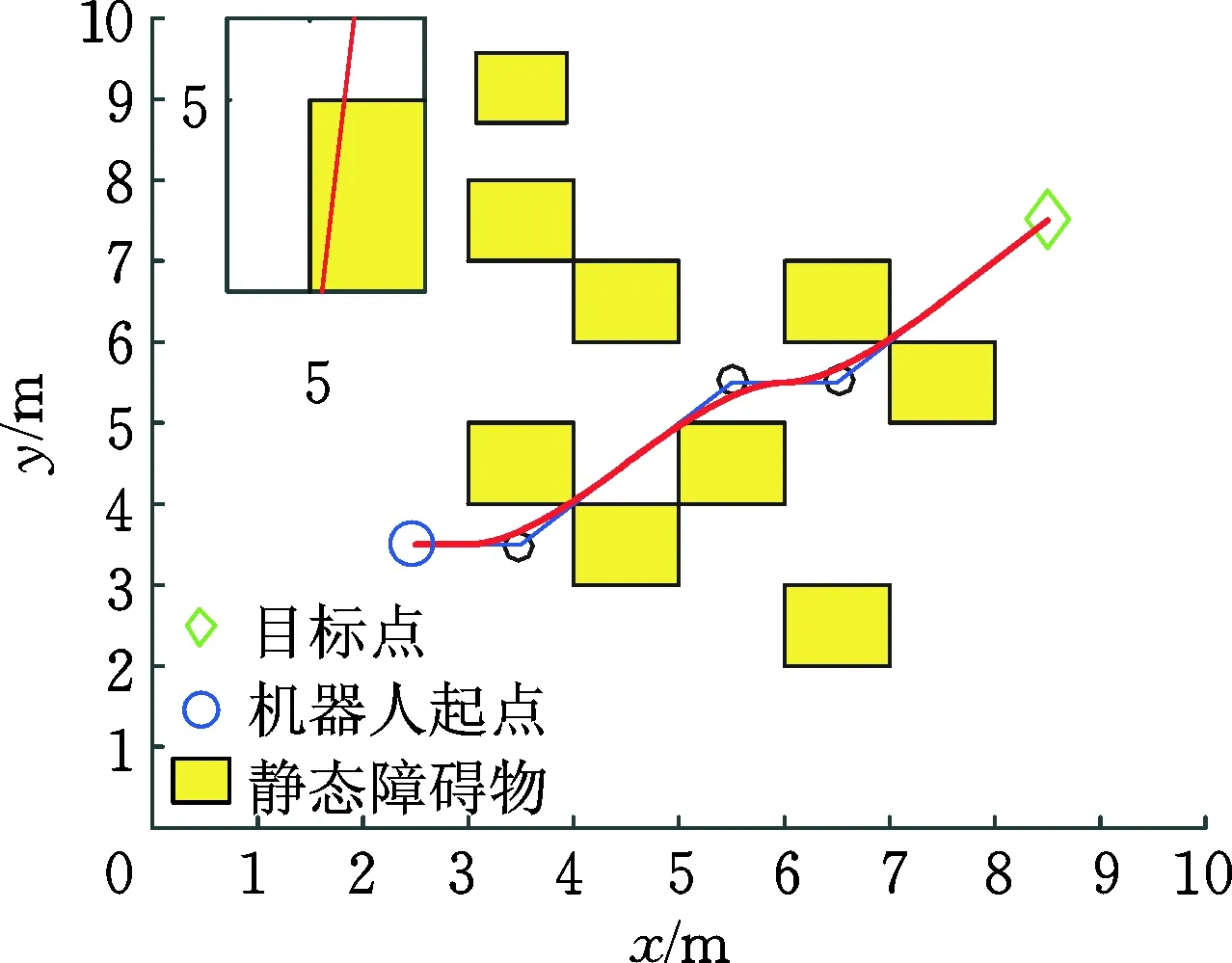
图5 三次B样条函数和A*算法的路径规划Fig.5 Path planning of cubic B-splines function and A* algorithm
3.2 动静态障碍物+动态目标
利用MATLAB软件对比改进的人工势场法与传统方法,其中参数选取根据经验法[23-25]、仿真环境和实验环境得到。为了有效对比算法的先进性,仿真过程两种算法的参数选取如下:m=2000,kv1=1000,k=100,kv2=1000,ρ0=0.5m,其他参数见表2,仿真结果如图6、图7和表3所示。
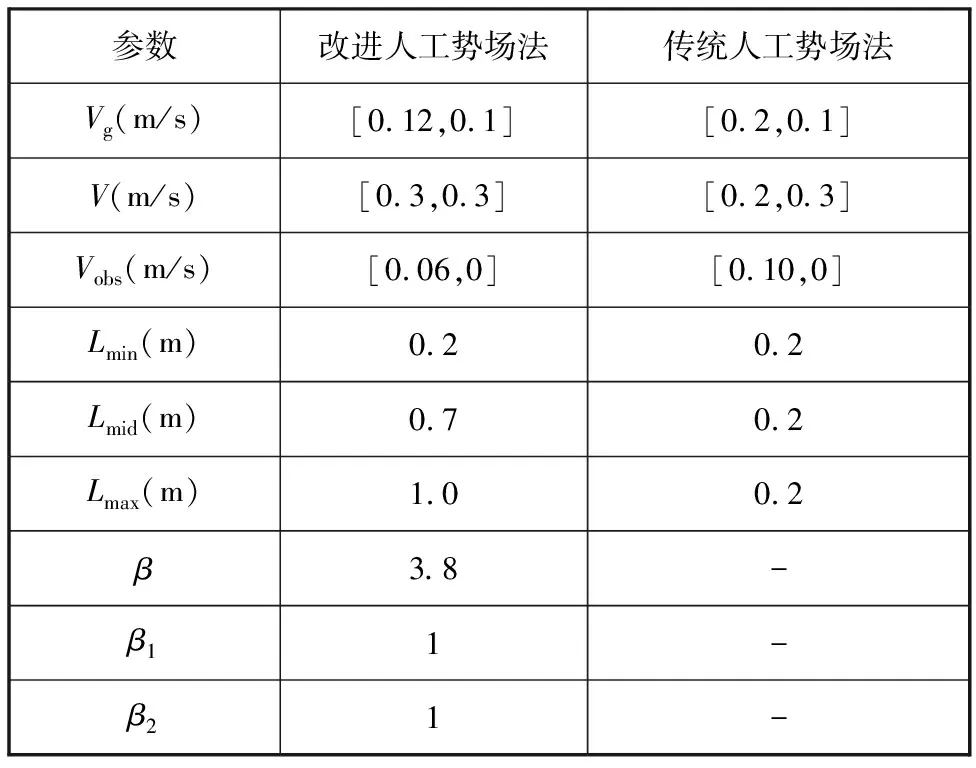
表2 实验参数
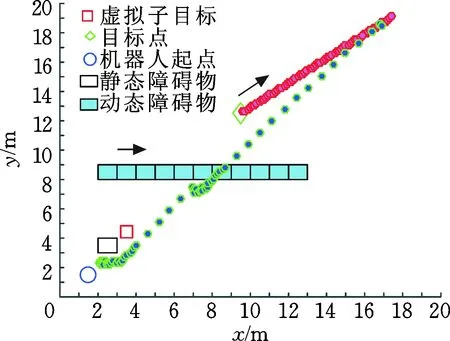
图6 改进的人工势场法的路径规划Fig.6 Path planning for improved artificial potential field algorithm
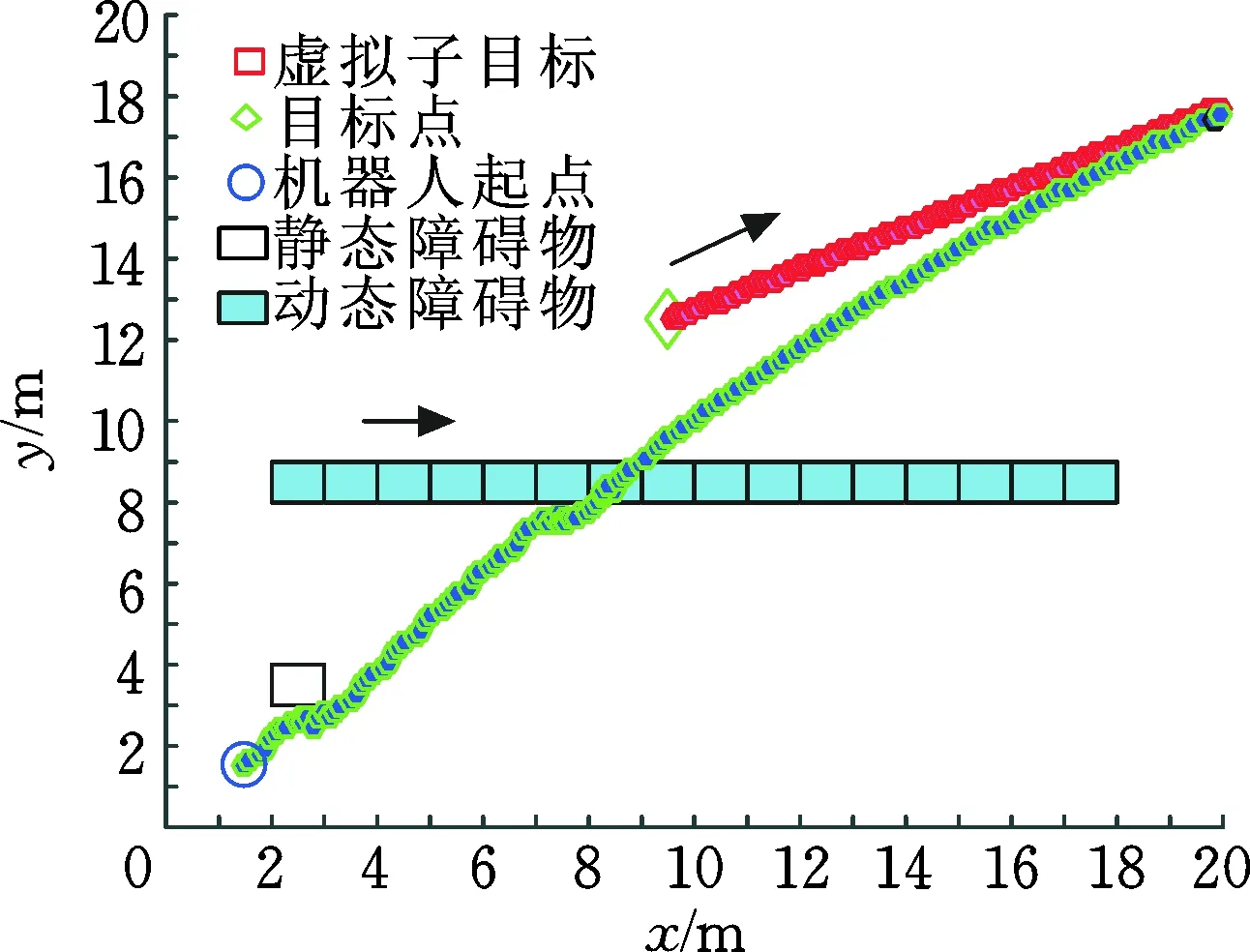
图7 传统人工势场法的路径规划Fig.7 Path planning for traditional artificial potential field algorithm
图7中,移动机器人在障碍物附近存在不良震荡现象。最终,运行步数为154。由图6的仿真结果可以发现,采用自适应步长调节算法既可以安全躲避障碍物,提高实时性,又能节省运行时间。总运行步数为54。由表3可以看出,相比传统人工势场法,所提算法运行时间和路径长度分别减少了18.6%和51.3%。
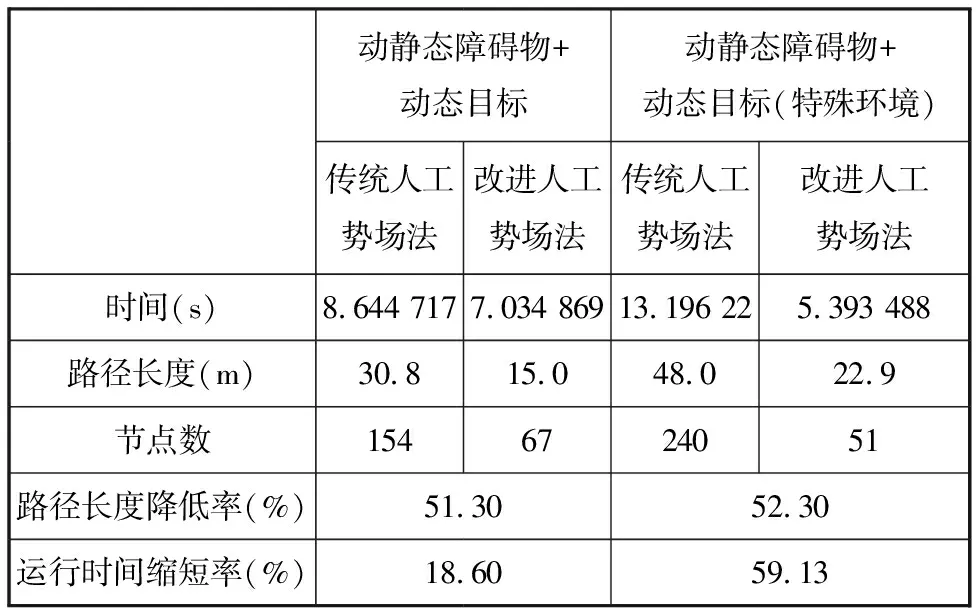
表3 算法仿真数据比较
3.3 动静态障碍物+动态目标(特殊环境)
机器人、障碍物和目标位置处于同一条直线,且障碍物位于中间位置时,机器人很容易陷入局部极小值陷阱。采用改进的人工势场法进行仿真实验,结果如图8、图9和表3所示。
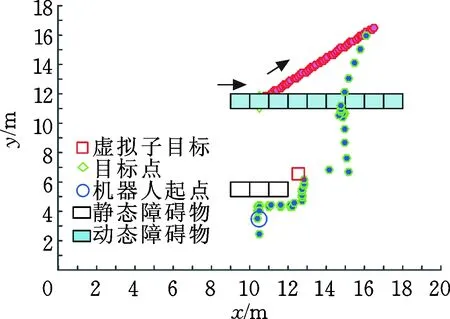
图8 改进的人工势场法的路径规划Fig.8 Path planning for improved artificial potential field algorithm

图9 传统人工势场法的路径规划Fig.9 Path planning for traditional artificial potential field algorithm
由图9可以看出,当引力和斥力一直处于同一条直线时,机器人无法有效地避开障碍物,一直在障碍物附近徘徊,无法向目标点移动。总移动步数为240。而在图8中,当移动机器人检测到陷入局部极小值陷阱时,增设的虚拟子目标及时的对移动机器人产生外力,帮助移动机器人摆脱了局部极小值陷阱,同时避免在障碍物群附近产生震荡。总的移动步数为51。由表3不难看出,相比传统人工势场法,改进的人工势场法在运行时间上缩短了59.13%,在最优路径长度上也减少了52.3%。
4 实验
本实验采用绿色圆形纸盒作为静态障碍物,两个3自由度QUANSER QBot2作为追踪机器人和动态目标,整个实验场地大小为2.5 m×3.0 m,栅格大小设定为0.6 m×0.6 m。机器人半径为0.17 m,障碍物半径为0.11 m,δ=0.15 m,实验参数设定m=1 200,kv1=1 000,k=200,kv2=1 000,ρ0=0.3 m,其余参数设定同表2。其中,红外摄像头实时传输目标机器人的位置信息。实验环境和实验情况如图10和图11所示。
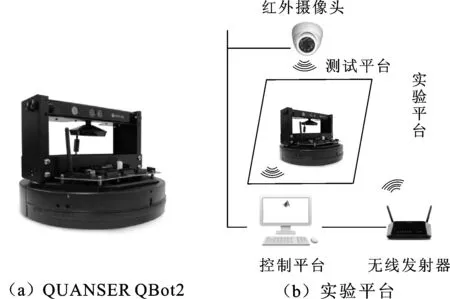
图10 实验设备Fig.10 Experimental Equipment

图11 路径规划实验情况Fig.11 Path planning experiments
图11中,机器人从起点(图11a)开始,在目标引力与障碍物斥力的合力作用下,实时完成避障(图11b),而且迅速跟踪移动的目标机器人。值得注意的是,机器人自身存在非完整约束,且试验场地地面较为光滑,故本实验中,机器人运行的转角较大。
5 结论
本文主要研究动态复杂非结构化环境下移动机器人的路径规划问题,提出了将全局规划算法与局部规划算法相融合的路径规划方法。基于新型A*算法,实现了移动机器人路径规划,利用二次A*算法与动态切点调整法对路径进行平滑处理,同时依据机器人环境感知信息和全局路径规划结果,采用基于自适应步长调节算法的人工势场法,实现了移动机器人局部路径的动态规划。最终移动机器人实现以较快速度沿着较短平滑路径追踪目标。通过对比分析,证明了本文所提算法的有效性。在后续的工作中,将结合图像对更多复杂环境进行进一步改进分析。

