面向混批加工的装夹方案选择与线平衡集成优化方法

张 恒 李爱平 傅 翔 邵 焕 刘雪梅

同济大学机械与能源工程学院，上海，201804

0 引言

装夹规划与线平衡是生产线构型选择的热点问题。装夹规划主要包括装夹方案选择、定位基准选择、夹具设计、加工元分类与排序等[1]，其中，装夹方案的选择对加工元排序分配及定位基准的选择有直接影响，线平衡是在装夹规划基础上的后序优化。对于单品种零件的装夹规划与线平衡问题，国内外学者对其进行了研究，取得了丰硕的成果。HAJIMIRI等[2]在零件装夹方案选择中考虑了夹具可达性约束、特征之间的公差要求与几何关系，以及定位基准面的选择。黄风立等[3]针对基于加工特征的计算机辅助装夹规划问题，综合考虑零件定位基准及进刀方向的选择，以装夹次数最小为目标，提出了一种基于多态蚁群算法的装夹规划优化方法。李蓓智等[4]针对装夹方案选择对薄壁型零件加工过程中形变的影响，提出了一种装夹方案与加工顺序综合优化方法。

近年来，业内学者提出了多种智能算法以解决单品种零件线平衡问题。ESSAFI等[5-6]针对机加工线平衡问题，提出了一种混合整数规划的数学模型以及基于GRASP算法的启发式算法。BORISOVSKY等[7-8]针对大规模机加工生产线平衡问题，提出了一种改进遗传算法以及动态规划法。DELORME等[9]基于贪婪随机自适应搜索策略，应用启发式算法来处理可重构机加工生产线多目标平衡问题。ÖCHÜ等[10]总结了装配线平衡与机加线平衡研究过程中存在优化目标单一、鲁棒性较差、经济性不高等问题。

针对装夹方案选择与线平衡集成优化的研究主要关注于单品种零件的加工生产。ESSAFI等[11]针对大规模机加工生产线平衡问题，在结合路径重构技术和随机自适应搜索策略的基础上，比较了不同装夹方案下的节拍、平衡率等指标情况。李爱平等[12]研究了不同装夹方案的选择对操作排序产生的影响，基于改进蚁群算法提出一种基于装夹选择的缸体零件柔性机加工生产线平衡优化方法。LIU等[13]针对复杂箱体柔性加工线的平衡问题，考虑了多种装夹方案组合及加工操作排序对线平衡率的影响。

目前，混流生产线的研究多集中在装配线领域，仅少量针对机加工生产线[14]，对解决多品种零件混批生产线装夹方案选择与线平衡集成问题的研究尚未深入。因此，研究解决多品种零件混批生产线的装夹方案选择与线平衡集成优化问题具有重要的理论价值与实际意义。

本文针对一类混批加工缸体等箱体类同族零件的生产线平衡问题，将装夹方案选择与线平衡进行集成优化研究，分析不同装夹组合下各零件的生产指标，并引入多零件批量比重系数。考虑加工操作间的多种约束关系，以节拍、夹具种类、平衡率和整线平滑系数为优化目标，构建混批生产线装夹方案选择与线平衡集成优化模型，并采用改进遗传算法对模型进行求解。最后，以某企业发动机缸体混批生产线为例，针对装夹方案选择与线平衡集成优化所得的生产线构型方案进行进一步的筛选，最终获取多种同族零件混批生产的生产线构型与操作分配方案，从而验证本文方法的有效性和高效性。

1 集成优化模型

1.1 问题描述

零件混批加工受到诸多因素的影响，不仅需分多个工位依次加工(每个工位配备一台或多台并行机床，各工位以统一的节拍串行加工)，而且要考虑多种零件共线加工时的批量、夹具选择、工位机床数配比，以期满足实际生产需求并实现节拍较短、生产成本较低的目标。装夹方案选择与线平衡集成优化前，各装夹工具对应的零件姿态、可加工面及其定位基准等已经确定，零件所有加工操作的加工方案(包括加工方法、加工时间、加工等级、所需刀具以及切削参数等)也已确定。在此基础上，以节拍、装夹种类数、平衡率、平滑系数为优化目标，先确定若干组可行的生产线构型方案(一个生产线构型方案是由一个装夹序列、多个工位以及每个工位配置若干机床的组合)；然后，将操作按照一定的约束条件分配至各工位；最后，从多个生产线构型方案中选择多种同族零件最优的生产线构型与操作分配方案。

1.2 数学建模

同族类零件具有相似的外形及加工部位，仅特征数量和尺寸略有不同[15]，因而可以用同一方式对其特征操作进行建模。设同族零件集合P={P1，P2，…，PL}，其中，L为零件个数。

假设一个零件有D个加工特征，可由向量F=(f1，f2，…，fD)表示，其中，fi为零件的第i个特征，i=1，2，…，D。第i个特征有m种加工方法，即加工链fi={O1，O2，…，Om}，其中，Oj表示特征fi的第j种加工链，j=1，2，…，m。由于加工链一般是由多个操作序列所组成的，因此Oj又可以表示为Oj=(O1,j,O2,j,…,Omj,j)，其中，Ok,j表示特征元fi第j种加工链中的第k(k=1，2，…，mj)个操作。为表述方便，直接用加工操作序列表示零件的加工工艺路线，即O=(O1，O2，…，On)，其中，n为加工操作总数。同时引入Oi=(IID,i,MTO,i,FFX,i,TTAD,i,TTI,i)详细描述加工操作Oi的工艺信息，其中，IID,i为加工操作编号，MTO,i表示采用的刀具，FFX,i表示所采用的夹具，TTAD,i表示该加工操作所在工位刀具可进刀的方向，TTI,i为加工时间。

1.2.1约束模型

零件加工必须要满足一定的约束条件才能保证其加工精度，获得良好的经济效益。加工约束主要分为以下几大类。

(1)工艺约束。根据特征之间的强弱关系，将工艺约束分为强制性约束和最优性约束。强制性约束为加工特征时必须遵循的约束，违反该约束会导致零件加工质量降低，甚至报废。最优性约束，即在加工过程中会影响加工经济性的约束，违反该约束不会对零件生产造成影响。

为更直观地表示加工操作之间的优先约束关系，引入加工顺序图G={O,S,Fp,Fb}。其中，S={S1,S2,…,Sns}为有向图中加工操作之间的边连线集合，ns为操作间的边连线总数。若加工操作之间有实线连接，则操作之间存在明确的先后关系约束且不可更改，否则操作之间没有明确的先后约束关系；Fp={Fp,1,Fp,2,…,Fp,np}为有向图中加工操作点的前序操作集合，np为前序操作总数；Fb={Fb,1,Fb,2,…,Fb,nb}为后序操作集合，nb为后序操作总数。

为便于后续算法求解，将操作加工顺序图以优先关系约束矩阵的形式保存。矩阵元素rij表示两个操作之间的优先关系，若加工操作Oi位于加工操作Oj之前，则rij=1，否则rij=0。按此规则得到零件加工操作的约束矩阵R=[rij]n×n。

据上所述，如果操作Oi属于零件加工操作集合O且rij=1(i≠j)，则存在对应的前序操作集合并将其定义为Fp,i。同理，如果操作Oi属于集合O，且rij=0 (i≠j)，则存在对应的后序操作集合并将其定义为Fb,i。

此外，还有一些特殊的工艺约束，如包含约束与不包含约束。定义包含约束为某些加工操作必须在同一装夹定位下完成。规划时，将包含约束合并为一个加工操作集，作为单个加工操作进行排序分配。不包含约束即对于某些特殊要求的加工操作，必须将其放于不同工位加工。对于不包含约束，在后续分配中应将它们分别分配至不同工位。

(2)装夹约束。定位基准的选择主要考虑工艺因素与结构因素。工艺因素主要考虑零件的加工精度，需要遵循一系列工艺准则，例如基准统一、基准重合、互为基准等。结构因素则考虑夹具结构，确保夹具内的工件定位准确、装夹可靠、机床进刀以及调整方便。

混批生产线设计需要选择一组柔性共用夹具FFX={FFX,1,FFX,2,…,FFX,nFX}以满足多品种零件共线生产的需求。不同的夹具对应不同的定位基准集合，不同的定位基准对应不同的操作，则有FFX,i={OFX,1,OFX,2,…,OFX,mFX}，其中，OFX,w为夹具中第w(w=1,2,…,mFX)个定位基准所对应的操作，mFX为第i种夹具所对应的定位基准总数。为某一工位选择夹具时，必须先确保其定位基准对应的特征在前序工位已加工完成，即存在定位基准约束。夹具在装夹过程中会对零件特征中的某一部分产生遮挡，影响进刀路径，形成刀具可达性约束。

(3)工位约束。由于生产节拍限制，需要对各工位分配时间进行约束，形成工位时间约束。考虑车间空间布局限制，对各工位的机床数量进行限定，则有单工位最大机床数量约束。

工位时间约束可由工位机床数和理论节拍得到：

TP(k)=T0M(k)

(1)

式中，TP(k)为k工位的限制时间；T0为理论节拍；M(k)为k工位的机床数。

最小工位数量LB与目标节拍T0、单工位最大机床数n0以及操作的总时间Tsum有关，满足

LB=Tsum/(T0n0)

(2)

为提高机床利用率，需对机床总数M进行限制。分析生产线布局可知，机床总数M不小于最大工位数。最大工位数可由生产对象的加工操作总时间和年产量得到。因此所需机床总数满足

(3)

式中，TV为企业一年实际的生产时间；Vl为零件l的目标年产量；Tsum,l为零件l的加工总时间。

1.2.2单品种零件生产线的常用优化目标

节拍是影响产量的最关键因素，平衡率是生产线平衡的重要技术指标。由于需要对夹具数量进行优化，因此将柔性夹具种数作为优化目标。整线平滑系数作为反映各工位负荷均衡情况的重要参考，也是本文所要考虑的，因此将生产节拍、夹具种数、平衡率和整线平滑系数作为优化目标，各目标描述如下。

(1)最小化生产节拍

minTC=min max(Ti)

(4)

式中，TC为所有工位节拍的最大值；Ti为第i个工位的节拍。

生产节拍越小，生产线效率越高。

(2)最小化夹具种数。本文在夹具选择时，对各工位可选夹具种类不做限制。一个生产线构型方案所选用的夹具种数为nFX。夹具种类应越少越好，因此，夹具种类数优化目标函数为minnFX。

(3)最大化平衡率为

(5)

PB反映整线的平衡情况，值越大，平衡效果越好。

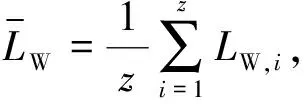
(6)

为简化评价体系，将上述多目标转化为单个综合评价目标。由于上述评价目标的量纲不同，因此需对其进行量纲一化处理。

1.2.3综合优化目标

(1)单品种零件生产线优化目标。为解决单品种零件的多个构型方案选择问题，比较单个零件在不同构型方案下的优化指标情况，引入综合优化目标：

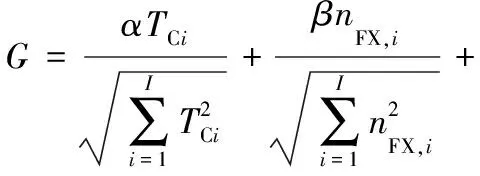
(7)

式中，优化目标比重系数α、β、ε、φ由企业按照生产经验和实际需求给出；TCi、nFX,i、PBi、FB,i分别为第i个构型方案对应的节拍、夹具种类数、平衡率与平滑系数；I为所有参与比较的构型方案总数。

为统一各目标的收敛方向，在综合目标中用1-PBi替换平衡率的目标值。

(2)多品种零件生产线构型方案的选择。混批生产线的构型方案需满足多种零件共线生产，故针对多品种零件在多种相同构型方案下的优化指标情况，引入多品种批量比重系数，建立优化目标函数：

式中，Wl,i为零件l的第i种构型方案的目标值；Con为所有零件相同构型方案的数量；Wi为所有零件的第i种共同构型方案目标值；λl为第l种零件的批量比重系数。

故本文的最终目标函数为

OF=min(W1,W2,…,WCon)

(9)

2 生产线集成优化算法

2.1 生产线构型选择方法

先分别求出每一零件最优的若干构型方案，再找出所有零件的相同构型方案，最后根据多品种综合优化目标选择最佳的构型方案。若遗传算法未能求得相同构型方案，则以目标产量最大的零件为对象，求出若干最优构型方案集合，再分别以该集合中的构型方案去验证其余同族零件在该方案下的优化目标，从而筛选出最优构型方案。零件l的最优可行构型方案集合Ql={Q1,l，Q2,l，…，Qm,l}，所有零件相同构型方案集合为

Q=Ω(Q1，Q2，…，QL)

(10)

式中，Ω(*)表示选出集合中相同元素。

2.2 改进遗传算法

遗传操作是遗传算法的关键步骤，交叉变异算子对子代种群选择起着重要作用，本文对交叉变异算子进行改进，使其自适应调整，便于算法全局寻优。

(1)编码过程即将零件所有需要加工的操作序列，按照工艺约束、装夹约束、工位约束排列为一个向量，形成染色体个体。解码过程即产生加工方案的过程，按照染色体个体中所有加工操作的先后顺序，结合每个工位的装夹约束与工位约束，依次将加工操作分配至各工位。

(2)采用最优替换法将子代中若干最优个体替换父代中相应数量的最差个体，该方法有利于较优子代被遗传下去，从而提高种群适应度。

(3)交叉算子Pc和变异算子Pm直接影响算法收敛性，故本文对其进行改进，使之自适应调整，加快算法全局寻优。Pc和Pm的调整方法为

(11)

(12)

式中，Pc,max、Pc,min分别为交叉概率的上下限；Pm,max、Pm,min分别为变异概率的上下限；fmax为种群的最大适应度；favg为种群适应度的平均值；fc为参与交叉的两个个体中较大的适应度；fm为参与变异的两个个体中较大的适应度；A为自适应函数的变化系数。

根据研究对象的复杂性，采用两点交叉策略，对2个染色体个体的编码串随机选取2个交叉点，然后交换双方基因，从而增加后代多样性，促使种群更好的繁衍。变异策略采取随机变异点方式，随机选取1个子代个体编码串中某一点为变异点，将其提取后，按照操作之间的先后约束关系放在该编码串的其他位置，从而形成新个体。

2.3 初始种群

为提高遗传算法运行效率，加快收敛，本文采用一种启发式方法生成初始种群。首先按照加工操作的先后约束关系将其分配至初始生成的可行构型方案，然后将满足可分配完所有加工操作的方案保留并按目标值升序排序，最后选择若干最佳方案作为遗传算法初始种群。为确保所生成的初始种群都为满足所有约束要求的可行解，需对每一个初始染色体进行验证。

2.4 算法流程

针对多品种零件混批加工的相关问题，对上述算法进行改进，本文设计的算法流程如图1所示。首先按照约束条件随机生成若干组可行的构型方案，然后将加工操作按照一定的约束条件分配至上述构型方案的工位，应用提出的混批策略对多个产品依次进行同样的研究，选择最佳的构型方案作为多品种零件混批加工的最终设计方案。

图1 算法流程Fig.1 Algorithm flowchart

3 实例分析

3.1 实例描述

本文以某企业2种典型同族发动机缸体零件混批生产线为例，对其进行装夹方案选择与线平衡集成优化研究，对多种不同装夹组合下的构型方案进行对比，验证本文方法与算法的有效性。

聚类处理后，同族缸体A总计有69个特征、149个加工操作，缸体B总计有78个特征、173个加工操作。在工艺路线的前期规划过程中，已整理完成缸体所有待加工特征的加工操作信息，限于篇幅，此处不作赘述。

依据企业生产要求，限定单工位配备的最大机床数为2，根据式(2)，工位数限定为5～9。根据市场需求，A缸体目标节拍为543 s，年产量为 9000台，B缸体目标节拍为590 s，年产量为21 000台。现企业有卧式四轴加工中心若干台，根据企业预规划得A缸体的加工总时间4 687.93 s、B缸体的加工总时间5 122.89 s，据式(3)计算得该生产线需投入机床数：

因此，机床总数至少为9。

表1所示为各夹具下缸体安装姿态以及可加工内容，零件的定位基准由企业直接给出。

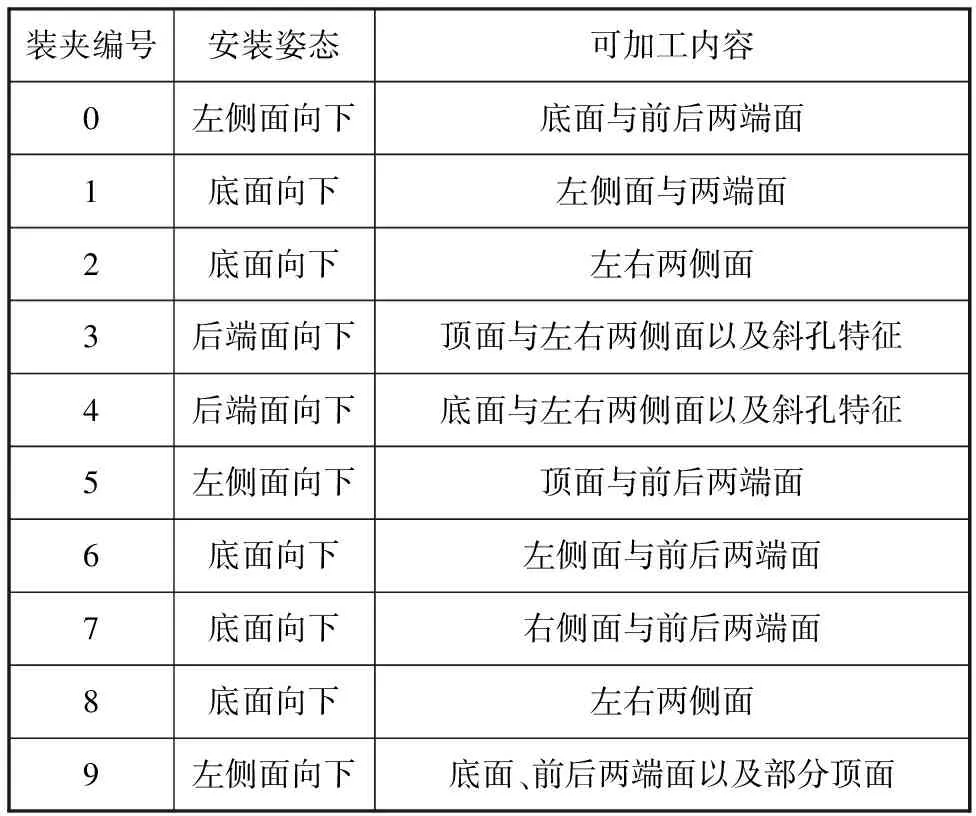
表1 各夹具下缸体安装姿态以及可加工内容

3.2 参数设置

设置初始种群大小G=200，交叉概率的上下限Pc,max=0.6，Pc,min=0.1；变异概率上下限Pm,max=0.06，Pm,min=0.01，A=5；根据多次测试结果，设置种群迭代次数gmax=200，构型方案搜索空间imax=500，零件总数L=2，最优构型方案总数T=20，案例中，根据企业生产指导文件以及实际生产经验，TV按300个工作日计算，工作日按两班制生产。α、β、ε、φ分别取0.8、0.05、0.1、0.05，λ1、λ2分别取0.3和0.7。

3.3 遗传算法改进前后对比

由于案例中两缸体具有相似性，因此，本文以A缸体为例验证算法有效性，将改进后的遗传算法与未改进的遗传算法进行对比(图2)，发现改进后的算法不仅收敛更快，而且能获得更好的最优解，只需经过64次迭代就能收敛，而改进前的遗传算法需经过120次迭代才能确保收敛。

图2 改进前后的遗传算法Fig.2 Unimproved and improved genetic algorithm

3.4 优化结果分析与讨论

应用上述集成优化方法以及改进的遗传算法，分别对2种缸体零件进行装夹方案选择与线平衡集成研究，得到2种缸体零件的10种最优构型方案及其相关指标，如表2、表3所示。其中，夹具组合每一位数字表示对应的夹具类型，机床组合每一位数字表示工位配置机床数从上述两缸体的最优构型方案中筛选出相同构型方案并对其进行重新编号，如表4所示。经计算，A缸体与B缸体的目标值WA与WB以及总目标函数值W如表5所示，易知1号方案的W最小，为最适合2种缸体混批生产的构型方案。

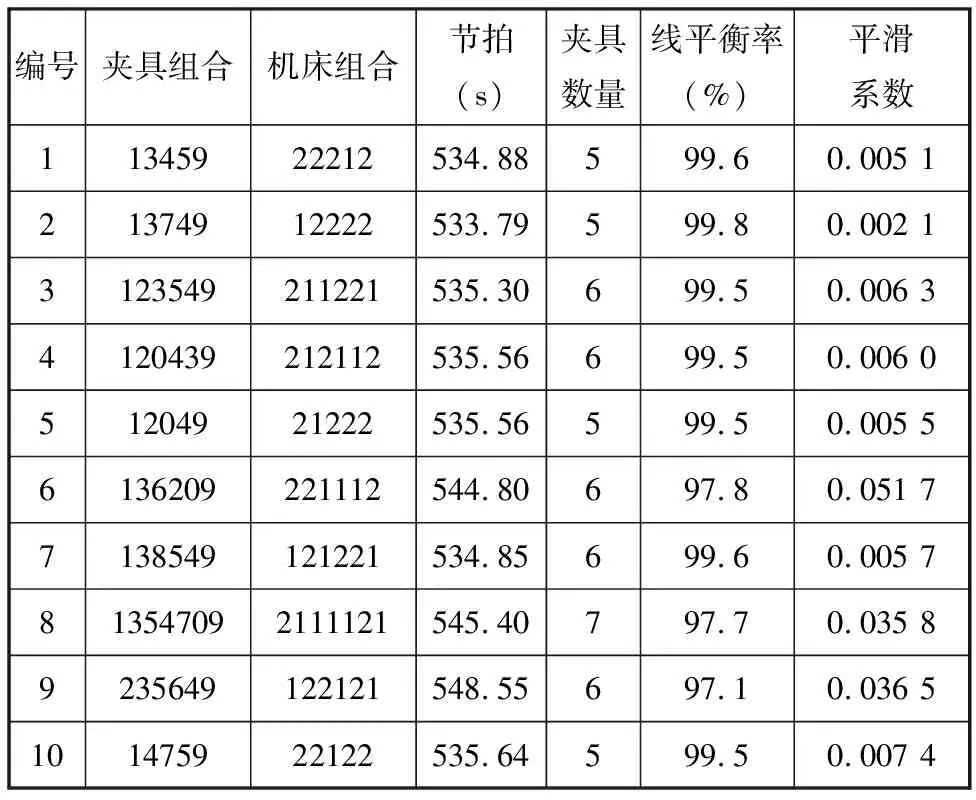
表2 A缸体不同装夹组合下的指标对比

表3 B缸体不同装夹组合下的指标

Tab.3IndicatorsofcylinderBunderdifferent fixturecombinations

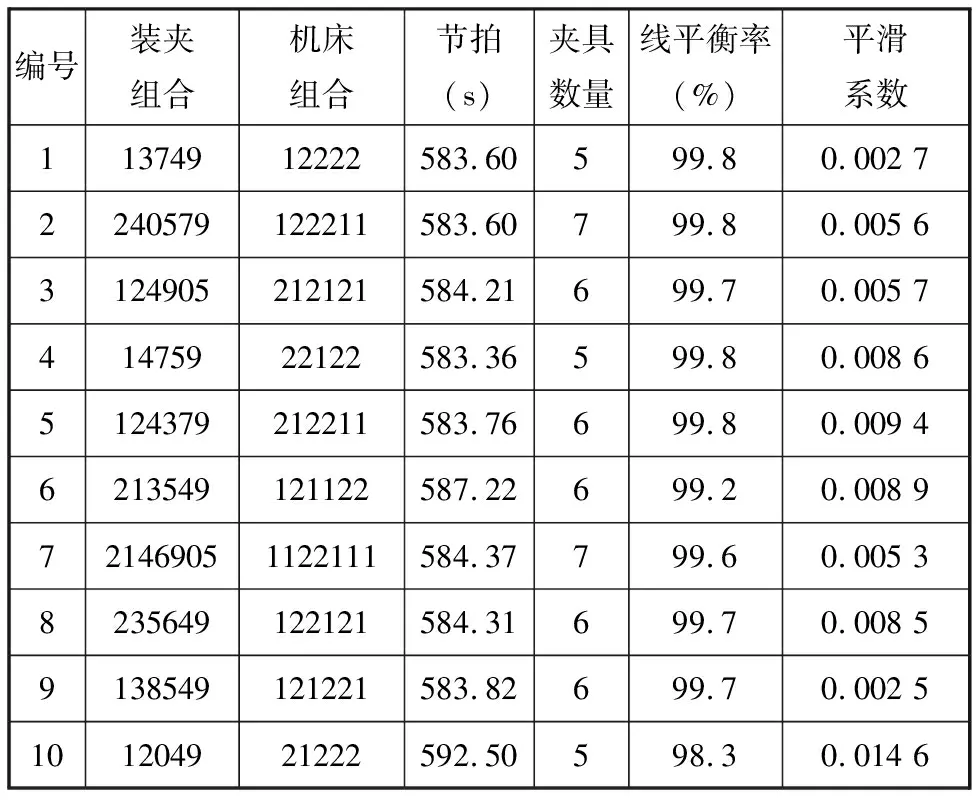
编号装夹组合机床组合节拍(s)夹具数量线平衡率(%)平滑系数11374912222583.60599.80.002 72240579122211583.60799.80.005 63124905212121584.21699.70.005 741475922122583.36599.80.008 65124379212211583.76699.80.009 46213549121122587.22699.20.008 9721469051122111584.37799.60.005 38235649122121584.31699.70.008 59138549121221583.82699.70.002 5101204921222592.50598.30.014 6

表4 两同族零件共同构型方案

表5 共同构型方案的优化结果

表6、表7所示为2种同族零件在1号方案中的操作分配情况，最小化生产节拍分别为533.79 s和583.60 s。为进一步验证本文模型的有效性，将装夹方案选择与线平衡分解成2个问题，对其进行串行研究，即在分别为每一工位确定可行装夹的同时，按照该工位可加工内容分配加工操作，直至所有操作分配完为止，得到一个可行的构型方案；如果分配不成功则舍弃。再对这些可行构型方案中的操作进行调整，进行线平衡研究，以期达到较好的平衡率。最后将串行模型求解结果与本文集成优化所求结果进行对比。由表8可知，对于2种零件，集成优化所求结果为24.78 s和53.37 s，较串行优化节拍分别减小4.64%与9.14%。2种方案在求解时都具有一定的优势，串行优化流程简单，集成优化所求得节拍更低，平衡率更好，优势更明显。因此集成优化比串行优化在优化结果和计算效率上均有较大优势。

与企业原规划方案相比，1号方案中的A缸体节拍减少39.33 s，B缸体节拍减少44.92 s，A、B缸体的线平衡率达到99.8%，提高约10%。按照两缸体3∶7的产量比，A缸体可生产9116台，比企业目标计划多116台，比企业规划方案多644台，B缸体可生产21 271台，比企业目标计划多271台，比企业规划方案多1 503台。

本文提出的混批策略不仅有效解决了多产品混批加工时的夹具选择、加工操作排序分配以及工位机床数配比问题，而且有效降低了零件的生产节拍，提高了平衡率。

表6 1号方案A缸体操作分配情况

表7 1号方案B缸体操作分配情况

表8 串行优化方案、企业规划方案与1号方案对比

4 结论

本文针对缸体等箱体类同族零件混批机加工中的装夹方案选择与线平衡问题，提出了多品种零件共线生产的装夹方案选择与线平衡集成优化方法。首先，在考虑多种约束和优化目标的基础上，对多种同族零件混批加工时的夹具选择、加工操作的聚类排序与分配、构型方案的选择，以加工操作为基本单位对其进行工艺优化。然后，对遗传算法进行改进：选择算子基于最优替代法，交叉变异基于自适应策略。采用一种启发式方法快速、有效地获取初始种群，提高算法运行效率。最后，以某企业混批生产线为例，按照企业实际需求获得了2种缸体加工的构型方案，以及各工位加工操作排序分配方案，在此基础上，将集成模型与串行模型求解的结果进行了对比，验证了模型的有效性。对算法给出的构型方案与企业原规划方案进行了对比，验证了所提方法的有效性和高效性。

本文研究对象只是针对同族零件，未来可考虑不同族零件小批量混批加工的装夹规划与线平衡问题，以及生产调度策略优化问题。