GLONASS卫星信号捕获研究
何国栋,方明星,宋 朋,何 昕
(1.安徽师范大学 物理与电子信息学院,安徽 芜湖 241003;2.中国电子科技集团公司第五十八研究所,江苏 南京 210000;3.安徽师范大学 计算机与信息学院,安徽 芜湖 241003)
0 引言
目前,全球有四大卫星导航系统:中国的北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)、俄罗斯的全球卫星导航系统(Global Navigation Satellite System,GLONASS)、美国的全球定位系统(Global Position System,GPS)和欧盟的伽利略GALILEO导航系统[1-2]。
GLONASS是俄罗斯开发并维护的全球卫星导航系统,最早由苏联研发,后由俄罗斯继续维持发展[3-4]。该系统于2007年开始运营,当初仅对俄罗斯境内提供导航和定位服务,到2009年,该服务范围拓展到全球,服务包括定位、测速等。截止该文章撰写日期(2019.7.15),GLONASS系统在轨卫星数量达到26颗,其中24颗正常工作,完成发射导航信号等各项工作,1颗卫星正在飞行测试阶段,1颗卫星正在试运行阶段。24颗卫星均匀地分布在3个近圆形的轨道平面上,这3个轨道平面两两相隔120°,同平面内的卫星之间相隔45°,轨道高度19 100 km,运行周期11 h 15 min。由于俄罗斯的地理位置原因,GLONASS系统轨道面倾角设计为64.8°,比GPS系统的轨道面倾角(55°)大,对高纬度地区的覆盖效果更好。与美国的GPS系统相比,GLONASS系统主要有3点不同[5]:① 信号体制不同,GPS采用的是码分多址技术,每颗卫星工作的频率相同,卫星间依靠不同的扩频码区分,扩频码长度为1 023位。GLONASS系统采用频分多址技术,卫星依靠不同的频率进行区分,信号也使用同一扩频码进行扩频,扩频码长度为511位;② 时间标准不同,GPS系统时间与世界协调时相关联,GLONASS与莫斯科标准时相关联;③ 坐标系不同,GPS使用的是世界大地坐标系,而GLONASS使用的是前苏联地心坐标系。
目前,国内外对GPS信号处理的研究较多[6-7],由于GLONASS卫星发射的载波频谱范围更宽,可以防止整个卫星导航系统同时被敌方电磁干扰,具有更强的抗干扰能力,因此对该系统进行研究具有重要的理论和实际意义。本文对GLONASS信号模型进行了分析,对其信号捕获的原理进行了研究,并用Matlab软件对几种捕获算法进行了对比分析。
1 GLONASS信号
GLONASS卫星发射的导航信号由导航电文、伪随机码和载波3部分组成[8]。卫星通过导航电文将卫星的相关信息发送给接收机,包括系统时间、星历、卫星运行健康状况和电离层时延修正参数等,导航电文速率为50 bit/s,经过明德码编码后,速率变为100 bit/s。GLONASS系统虽然是频分多址系统,但是为了提高系统的抗干扰能力,对导航电文也进行了扩频调制,伪随机扩频码速率为0.511 Mbit/s。GLONASS系统使用的伪随机码是周期为1 ms的M序列,从9级移位寄存器的第七级输出,序列的初始化矢量是(111111111),对应的9阶移位寄存器生成多项式为:
G(x)=1+x5+x9。
(1)
扩频后的导航电文通过二进制相移键控的方式调制到不同频率的载波,GLONASS卫星发射的导航信号有L1和L2两种载波频率,分别为:
L1 载波:f1=1 602+0.562 5*k(MHz),
(2)
L2 载波:f2=1 246+0.437 5*k(MHz);
(3)
式中,k为每颗卫星的频率编号,基于L1载波的卫星之间的频率间隔为0.562 5 MHz,L2载波导航信号产生的原理与L1相同,卫星之间的频率间隔为0.437 5 MHz。
接收机射频前端接收的GLONASS卫星信号通过下变频后变为中频信号[9],L1频带上第k个卫星信号的数学表达式为:
Sk(t)=C(t)Dk(t)cos[(ωI+k×0.562 5+ωd)t+θk]+n(t),
(4)
式中,C(t)为GLONASS系统的伪随机码,所有卫星均相同;Dk(t)为卫星发送的导航电文,ωI+k×0.562 5为下变频后第k颗卫星对应的载波频率,为了节省频谱资源,GLONASS系统应用对拓技术。因此,k的取值范围为-7~6,ωd为由于卫星和接收机相对运动产生的频率偏移,称为多普勒频率,θk为载波相位,n(t)为信号传播过程中受到的噪声干扰。
2 GLONASS信号捕获算法
捕获的目的是为了确定视线范围内的卫星,并粗略估计可见卫星的多普勒频率和伪码相位,接收机根据这些参数进行下一步的信号跟踪。捕获中有多普勒频率和伪码相位2个参数需要确定,是一个二维的搜索过程。接收机复现可能的伪码相位和卫星的频率,将复现信号与真实信号进行相关运算,当复现的信号与接收的卫星信号参数一致时,会得到一个很大的相关值,而其余值相对较小,接收机根据相关峰值确实是否捕获到对应的卫星。常用的捕获算法有串行捕获算法和并行捕获算法[10-11],下面对其进行分析介绍。
2.1 串行捕获算法
串行捕获算法是常用的一种扩频信号捕获方法,该方法将可能的伪码相位和多普勒频率全部复现并组合,再与卫星信号进行相关。卫星中频信号先与接收机的伪码相乘,再与接收机产生的载波进行相乘,由于载波信号的相位未知,需要分别与载波信号的同相I支路、正交Q支路进行相乘,将两路信号积分并平方相加。如果最后的相关值有明显的相关峰值,达到了捕获门限值,捕获成功,根据相关峰值的位置确定卫星信号的伪码相位和多普勒频率值,串行捕获算法原理图如图1所示。
2.2 并行捕获算法
并行捕获算法有并行频率捕获算法和并行码相位捕获算法2种[12]。并行频率捕获算法将接收的GLONASS中频信号与本地复现的伪码进行相乘,实现伪码剥离,然后运用离散傅里叶变换(Discrete Fourier Transform,DFT) 即可对实现对信号的频率分析,实际操作中运用DFT的快速傅里叶变换(Fast Fourier Transform ,FFT)。并行频率捕获算法原理图如图2所示,本地复现所有可能的伪码相位,如果本地伪码相位与卫星信号一致,FFT后会有较强的峰值。由于GLONASS系统采用了同一种扩频码,该方法一次遍历就可以检测到视线范围内的卫星,速度较快,但由于码相位较多,复杂度仍然较高。
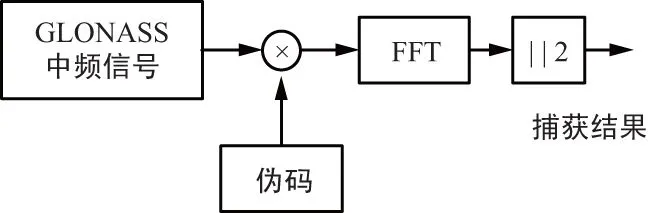
图2 GLONASS并行频率捕获算法原理图
并行码相位捕获算法基本原理是将2个序列的时域循环相关转换为频域的简单相乘运算[13-14],2个长度为N的序列x(n)和y(n)循环互相关定义为:

(5)
对式(5)进行N点离散傅里叶变换,得到:

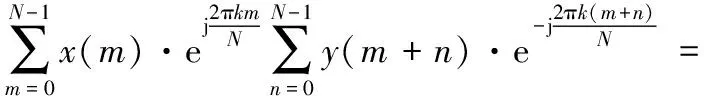
X*(k)·Y(k)。
(6)
式中,DFT表示离散傅里叶变换,其中X*(k)为x(n)的傅里叶变换后取复共轭,Y(k)为y(n)的傅里叶变换。根据这2个公式,可以对GLONASS捕获算法进行改进。将中频信号与本地载波信号进行相乘,并对其进行傅里叶变换得到Y(k)。对伪码进行傅里叶变换并取共轭,得到X*(k),将二者相乘后进行傅里叶逆变换,即可实现码循环搜索,得到卫星信号的伪码相位,并行码相位捕获原理图如图3所示。

图3 GLONASS并行码相位捕获算法原理图
3 捕获仿真与分析
串行捕获算法和并行捕获算法各有优缺点,采用Matlab软件对GLONASS的L1载波信号进行仿真验证,并对算法复杂度进行分析对比。
3.1 捕获仿真
GLONASS信号下变频后的中心频率设置为fc=5.5 MHz,采样频率为40 MHz。GLONASS在轨卫星有14个频道,L1载波信号频率间隔为0.562 5 MHz,每颗卫星各自的频率中心为fc+k×0.562 5 MHz,k的取值范围为(-7~6)。GLONASS卫星选用0号卫星,随机设置伪码相位和多普勒频率值fd,多普勒频率变化范围设置为±5 kHz,频率搜索步长设置为500 Hz,伪码相位搜索步进为半个码片。由于GLONASS扩频码一个周期的长度为1 ms,所以选择用于捕获的信号长度须为1 ms,即一个伪码周期长度,信噪比设置为-25,-30 dB两种情况。
仿真实验结果如图4所示,从图4 (a)、图4(c)和图4(e)可以看出,在-25 dB的信噪比下,3种捕获算法均能正确地捕获到卫星导航信号,得到较强的相干峰。在图4(c)中,由于FFT分析有负的镜像频率,所有产生2个相干峰。在-30 dB的信噪比下,由于干扰太强,3种捕获算法均不能有效地捕获到卫星导航信号。

图4 3种捕获算法捕获结果
3.2 复杂度分析对比
串行捕获是一个多普勒频率和码相位相联合的二维搜索过程,对于低动态接收机,多普勒频率搜索范围为±5 kHz,搜索步进为500 Hz,遍历511个不同的码相位,每半个码片搜索一次,搜索总共需要的重复相关运算次数为:
(7)
即总共需要21 462次相关运算才能完成对一颗卫星的捕获。串行捕获算法原理简单,易于实现,缺点就是需要对所有可能的情况进行分析,计算量较大,捕获的速度相对较慢,更适宜于硬件来实现。
并行频率捕获算法中每复现一次伪码相位,就运用FFT对载波的频率进行分析,通过分析频谱的值实现对卫星信号的捕获。由于GLONASS系统所有卫星使用同一扩频码,如果每半个码片搜索一次,则1 022次重复搜索就可以实现对视线范围内所有卫星的捕获。并行码相位捕获算法中,需要对频率进行遍历,对于一颗卫星,以500 Hz的步进对±5 kHz频率范围进行搜索,仅需要21次重复搜索。伪码的FFT变换结果可以预先存储在内存中,因此并行码相位捕获算法相对效率较高。
在同一台电脑上运行3种捕获算法,从表1中可以看出,串行捕获算法重复次数多,运行一次捕获需要时间最长,而并行码相位算法重复次数少,捕获时间最快,但是对于全网卫星,2种捕获算法还需要重复14次。并行频率方法一次捕获需要1.472 s,但是一次可以对全网进行搜索。
表1 算法复杂度分析

捕获算法重复次数复杂度捕获时间/s串行捕获21 462低5.242并行频率1 022中1.472并行码相位21高0.058
4 结束语
本文研究了GLONASS信号构成和特点,介绍了卫星导航信号捕获的串行捕获方法,并对应用快速傅里叶变换实现的并行频率和并行码相位捕获方法进行了分析。在同一机器平台上应用Matlab软件生成了1 mm GLONASS中频信号,验证了3种捕获算法在-25 dB的信噪比下对卫星信号捕获的可行性,对GLONASS的应用和开发具有重要的理论和工程意义,为我国的北斗系统研发和应用提供帮助。

