基于ICP算法的头部模型配准方法研究

白兰兰，邓双城，朱润泽，邓宁升

(北京石油化工学院，北京 102617)

经颅磁刺激是一种能够无创伤地在大脑中产生局部刺激的方法，通过刺激大脑的相应的功能区达到治疗效果，可用于治疗抑郁症、狂躁症、帕金森病、癫痫、中风等精神及神经科疾病。目前，经颅磁刺激是由医生手动放置控制线圈的位置，依赖于医生的经验，为提高经颅磁刺激的治疗效果需要准确把握刺激部位，因此需要将拍摄的MRI影像三维重建之后与患者真实头部进行配准。笔者利用点云配准技术实现头部模型的配准。

配准技术的应用最早出现在医学诊断和图像处理领域[1]，将功能影像和解剖结构影像结合起来，在同一幅图像上表达多种信息，同时反应人体的内部结构和功能状态，帮助医生进行医学诊断，目前配准技术广泛应用于逆向工程、机器人和虚拟现实等新的技术领域。点云配准是指将不同坐标系下的两片或多片点云数据，经过一定的旋转和平移变换使其统一到同一坐标系下。目前，几种常用的算法为ICP系列算法(经典ICP算法及改进ICP算法)、基于特征的配准方法和基于RANSAC(random sample consensus)的方法。1992年，Besl和Mckay利用四元数算法实现了自由曲面点云配准的迭代最近点算法，即ICP(Iterative Closest Point)算法[2]。ICP算法的基本原理是对于一片点云中的每一个点，在另一片点云中寻找距离该点最近的点作为其对应点，形成了对应点对，计算对应点对的欧式距离的平方的平均值，利用迭代算法使其平均值最小化，并不断更新两片点云的相对位置。因此，ICP算法是在不断重复“寻找目标点云集与源点集中距离最近的点—计算新的刚性变换矩阵并计算匹配误差”，直到满足收敛条件才停止迭代。

经典ICP算法存在局限性：(1)收敛速度及配准结果受初始位置的影响较大；(2)算法容易收敛到局部最优而非全局最优；(3)在搜索目标点的最近点时，每次都必须计算源点集中的每一点，算法的时间复杂度非常高；(4)经典ICP算法要求两个点云集必须是严格的包含关系。尽管原始的ICP算法存在一些局限性，但它为点云配准提供了一种很好的解决思想，因此，许多学者在经典ICP算法的基础上进行改进。Zhang等[3]采用k-dtree算法搜索对应点；Dorai C等[4]采取随机采样的方式选取对应点对，以加快搜索对应点的速度。Pulli等[5]采用距离的百分比衡量误差，将距离过大的10%的点对删除；Godin等[6]将纹理一致性和顶点的法向一致性作为约束条件，从而删除无效的对应点对，改进算法的迭代条件。Chen等[7]用一种基于点到切平面的欧氏距离代替原始ICP算法中基于点对点的欧氏距离；Turk G等[8]提出一种基于点到投影的评价函数。

1 初始配准

由于ICP算法容易受初始位置的影响，因此在利用ICP算法精确配准之前，先对两片点云进行初始配准。初始配准是将原本相距甚远的两点云集通过旋转和平移变换使其处在大致相同的位置。

常见的初始配准方法有：标签法[9]、重心重合法[10]、特征提取法[11-12]。标签法是指在测量时人为设置一些标志点，根据这些标志点进行定位，但此方法对仪器及人工经验的依赖度较高；重心重合法是计算两点云的重心，之后将两重心重合，此方法无法解决旋转错位；特征提取法是指提取轮廓曲线等，将表面特征相同的部分重合来实现初始配准，此方法只适用于具有突出特征的点云。

采用能考虑全局点云的主成分分析法(Principal Component Analysis，PCA)算法[13-15]，通过识别两点云数据的主轴走向和主要形态特征得到两点云数据的转换矩阵。PCA算法是一种广泛应用的数据降维的算法，通过将点云数据精简，留下点云集中贡献最大的特征。设一点集为P={p1,p2,…,pn}，首先求其均值并计算点集的协方差矩阵cov。协方差矩阵cov的3个特征向量作为点集P的空间直角坐标系的3个坐标轴，并以均值为坐标系的坐标原点。计算源点集点云数据对应目标点集点云数据的坐标变换矩阵参数，使用坐标变换矩阵参数将源点集数据统一变换到目标点集数据所在的空间直角坐标系上。经过初始配准之后，两点云基本统一到同一坐标系下，为之后的ICP算法提供了良好的初始位置。

基于PCA算法的初始配准步骤如下：

(1)对源点云集和目标点云集进行矩阵构建：

目标点云矩阵

(1)

源点云集

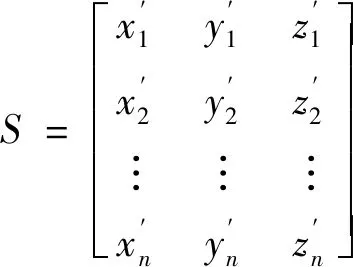
(2)

(2)计算两点云集的质心分别为μT和μS：

(3)

(3)分别对两点云矩阵求协方差：

目标点集点云协方差矩阵为

(4)

源点云协方差矩阵为

(5)

其中:X、Y、Z和X′、Y′、Z′分别为目标点集矩阵和源点集矩阵的3个列向量。

(4)求解两点云协方差矩阵的特征向量和特征值，并将特征值降序排列，得到两特征向量矩阵T1和T2：

T1=T2*(T*R)

(6)

其中：T表示矩阵T2到矩阵T1的平移矩阵；R表示矩阵T2到矩阵T1 的旋转矩阵。

(7)

至此，完成源点集与目标点集的初始配准过程。

2 ICP算法的解算步骤

S和T分别表示源点集和目标点集，可表示为

S={Si}i=1,2,3,…,n

T={Ti}i=1,2,3,…,m

(8)

旋转变换向量用单位四元数表示为qrotat=[q0,q1,q2,q3]T[1]，并且q0≥0,q02+q12+q22+q32=1,旋转变换矩阵可表示为R(qrotat)。设平移变换向量为qtrans=[q4,q5,q6]T，则求对应点对间的欧式距离之和最小化问题转化为求解qrotat、qtrans使函数f(qtrans,qrotat)最小化问题。

(9)

算法计算步骤如下：

(1)计算目标点集和源点集的重心分别为μT和μS:

(10)

(2)根据点集S和T构造协方差矩阵：

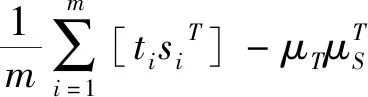
(11)

(3)根据协方差矩阵构造4×4：

(12)

(4)计算Q(ΣT,S)的特征值和特征向量，其最大特征值对应的特征向量为最佳旋转向量qrotat，则最佳旋转矩阵为：

(13)

(5)计算最佳平移向量为：

qtrans=μT-R(qrotat)μS

(14)

采用均方根误差(Root Mean Square Error，RMS)进行精度评价，均方根误差可表示为：

(15)

3 实验

本文中的算法采用Matlab编程实现，实验中最大迭代次数预设最大值为200，针对头部模型点云数据进行实验，并通过采样精简点云数量，从而减小程序的运行时间。实验的硬件环境为i7-8550U 2.00 GHz处理器，8 G内存，Win10 64位系统，基于Matlab平台进行测试实验。

图1 原始数据Fig.1 Head primitive point cloud data

目标点集包含68 421个点，源点集包含40 556个点。进行PCA初配准之前，两点云初始位置如图1所示，对两点云集进行PCA初始配准之后，两点云之间的相对位置如图2所示。由此可见，PCA初始配准使两点云集的位置初步调整，使其基本处于相同位置。

图2 PCA初始配准后Fig.2 Point cloud data after PCA initial registration

选取约100 000个点作为目标点集，源点集分别进行随机采样精简点云数量依次为90 000、80 000、70 000、60 000个点，如图3所示。目标点集与各源点集的初始位置相同进行点云配准，记录配准过程所需时间。实验结果如表1所示。

图3 目标点集与精简的源点集 Fig.3 Target point set and reduced source point set

由表1可知，精简点云数量能够减少程序运行的时间，但同时均方根误差RMS在增加，即ICP算法的精度稍微降低。因此在实际应用中可以在保证配准精度的前提下，合理地精简点云数量，有效提高算法的效率。

表1 不同数量点云ICP算法耗时对比

Table 1 Time-consuming comparison of different point cloud ICP algorithm

点云数量/个耗时/sRMS/mm90000221.260.090278980000198.530.090499270000162.350.091023660000129.790.0912947

在经颅磁刺激治疗中，患者真实头部点云的获取欲采用在其头部选取点，形成能够代表真实头部的点云。因此实验中采取在头部模型上沿着眉毛在头部表面选取一周的点，以头顶为中心放射状向下选取点直到与沿眉毛选取的那一周点重合，共选取约200个点形成1个“帽子”形状的点云集，同时选取易于识别的左右2个眼角及鼻尖3个点作为特征点，如图4所示。将此“帽子”形状的稀疏点云数据与一个完整的头部点云数据进行配准。经过ICP算法配准之后，如图5所示，均方根误差为0.080 0821 mm。

图4 “帽子”形的头部点云Fig.4 Cap-shaped point clouds

图5 ICP配准Fig.5 Registration of ICP algorithm

4 结束语

头部是人体中最重要的组成部分，随着科技和医学的快速发展，越来越多的头部顽疾能够得以治疗，头部配准技术是很多头部手术的关键技术，头部配准的精度对治疗效果的好坏有直接影响。利用PCA算法进行初始配准，之后用ICP算法进行精确配准。通过精简点云数量提高算法的计算速度。同时采集了稀疏点云数据与完整模型进行了配准实验，并取得良好的效果。然而，算法还可以通过采用k-dtree搜寻最近点，利用三维网格分割技术将目标点集中多余的部分删除来减少运行时间，这也将成为下一步研究的内容。