基于弯曲理论的动调轴流风机叶片三维造型

张志莲，王铃玉*，杨创峰，江 朝，吕 涛，徐 康，聂 帅

(1.北京石油化工学院机械工程学院，北京 102617; 2.成都成发科能动力工程有限公司，四川成都 610052;3.北京工业大学环境与能源工程学院，北京 100022 )

动调轴流风机因具有较宽的高效工作区等优点而广泛应用于冶金、电力和煤矿等工业，并且在热电厂、矿井、隧道等都发挥了良好的节能作用。动叶是动调风机能量转化的主要部件[1-2]，为了满足不同安装角下风机良好的气动性能，叶片翼型各异，叶片外表曲面复杂，叶片整体呈扭曲状，各截面弦长和弯曲角也各不相同，因此构建扭曲叶片的三维造型过程复杂，对于造型的方法更是引起研究者广泛关注。王刚等[3]利用双三次B样条逼近曲面拟合叶面，但精度不高，最大相对误差为0.054%；高丽[4]和王海松[5]对曲面叶片进行造型，将型线计算结果生成数据文件导入Pro/E软件，利用边界混合或曲面融合形成实体；陈亚琼等[6]建立参数化数学模型，将综合翼型泛函集成理论与B样条曲线拟合建模，对叶片进行参数化处理；张大庆等[7]利用若干段不同直径的圆弧围成截面叶型，再将各截面叶型混合成型，得到叶片实体模型，同时利用B样条曲线插值对曲率进行优化，得到高斯曲率最大值为0.0001的光顺曲面；何元新[8]在Pro/E中通过多次延伸曲线解决了叶片根部与轮毂之间的间隙问题。廉玲军[9]和黄文俊[10]将各截面曲线坐标以数据文件分别导入Pro/E和Solidworks中形成叶型曲线，选用NURBS曲线绘制各截面曲线再对叶片曲线进行缝合；田庆等[11]提出叶片界面线拼接的方法，用曲面放样再缝合得到叶片几何模型，并对UG软件进行二次开发，使用户可以直接由点文件格式生成叶片造型，简化了叶片造型过程；宁小波等[12]生成了叶型上下表面的坐标值的txt文件，导入Solidworks中形成叶型上下轮廓曲线，利用分割线切割出叶片截面的投影曲面，再进行放样生成叶片三维造型，由此得到的叶片各截面二维翼型产生微量误差，对后续进行的气动分析结果也会产生相应误差。

在设计轴流风机叶片时，对整个叶片从叶根到叶顶取一定数量的不同半径基元级截面作为计算截面[13]，为了便于设计计算将基元级截面展平成二维进行计算[14]。因此，叶片三维轮廓曲线应该极度贴合理论计算的叶片数据弯曲到各个基元截面上的尺寸，以提高后续的气动分析结果的准确度和可靠度。由此建立叶片截面弯曲理论，利用Solidworks的包覆功能加以实现，并对包覆形成的三维轮廓曲线进行理论验证。该叶片造型方法可推广到多种轴流风机及压气机叶片设计中。

1 叶片设计过程

采用叶栅法设计了某型号动叶可调轴流风机动叶，翼型选择NACA-65标准翼型，动叶各截面的翼型坐标如表1所示。以翼型中线为基准得到叶片吸力面和压力面的叶型轮廓点；利用三次样条曲线生成二维平面叶型并进行前缘、尾缘修正；将拟合后的二维平面翼型进行重心积叠，并调整翼型中线与x轴的夹角，使其等于计算所得的各截面翼型安装角；利用Solidworks包覆功能将二维平面翼型弯曲成三维轮廓曲线，并进行放样构建三维扭曲叶片造型。

表1 各截面翼型y坐标值

2 叶片截面弯曲理论

风机叶片由多个复杂曲面构成，可以通过三维轮廓曲线拉伸而成，而三维轮廓曲线是由二维平面翼型弯曲到圆弧基元截面得到。根据标准翼型及设计参数，通过计算得到二维平面翼型各点坐标值，再根据弯曲理论得出对应三维轮廓曲线的坐标值。

以二维翼型轮廓上一点A为例，x′为二维平面翼型上的A点在x轴方向上的坐标长度，以y轴为基准进行弯曲，使叶型轮廓曲线完全贴合圆弧截面，弯曲后A点落在B点位置，x为弯曲后得到的三维轮廓曲线在x方向上的坐标长度。叶型弯曲后B点与原来A点比较在y方向上没有发生变化，因此，y坐标长度不变，弯曲后点B相较点A在z方向上产生坐标值，如图1所示。

图1 叶片截面弯曲理论示意图Fig.1 Schematic diagram of blade section bending theory

原有的x′长度值弯曲后变为圆弧的弧长，根据B点所在圆弧半径R并通过公式求得圆弧夹角θ。根据夹角θ可以进一步得到x和z的值：

θ=x′/R

(1)

x=Rsinθ

(2)

z=R-Rcosθ

(3)

实际扭曲叶片的轮廓曲线上各点坐标应符合叶片截面弯曲理论。“包覆”理论验证如图2所示。由图2中可以看出，通过对简单的长方形进行理论验证，二维平面上的长度和包覆在基元级截面上的圆弧弧长一致，验证包覆功能得到的点坐标值与理论数据相符合，说明Solidworks的包覆功能法能够用于解决叶片三维造型中遇到的造型误差问题。

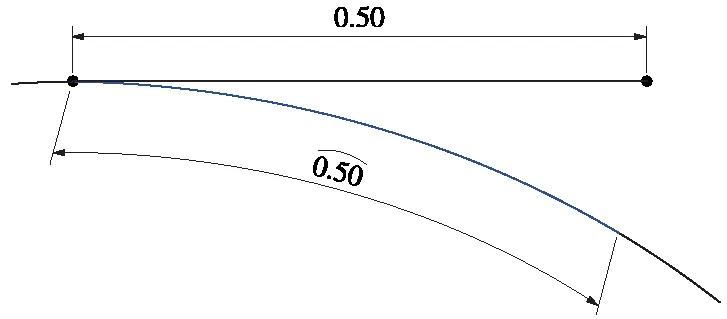
图2 “包覆”理论验证Fig.2 Experience of cladding function

将通过包覆功能得到的三维轮廓曲线与通过投影曲线得到的轮廓曲线进行对比，以叶顶截面翼型为例，前缘尾缘的对比结果如图3所示。红色线是投影得到的轮廓曲线；黑色线是包覆得到的轮廓曲线，与理论计算轮廓曲线相一致，按照投影曲线得到的三维轮廓曲线具有一定误差。

图3 三维轮廓曲线对比Fig.3 Contrast with three-dimensional profiles

3 基于Solidworks叶片三维造型

3.1 建立叶片截面

三维扭曲叶片由从叶根部至叶尖部之间多个三维轮廓曲线拉伸拟合而成。在用Solidworks构造叶片三维造型时，选择叶根与叶尖之间的平面截面进行二维平面翼型草图绘制。为了提高叶片造型的精准度，叶片截面从叶根到叶尖处选取7个截面，理论计算得到的翼型数据是将各个环形基准截面展平成二维平面截面上绘制得到的。

在Solidworks操作环境下，以上视基准面为基准，分别以等距圆弧截面半径为距离建立7个平面基准面。在前基准面上建立草图，绘制轮毂所在圆和叶顶所在圆，并根据选择的7个截面绘制2个圆之间的其他圆，对7个圆进行曲面拉伸，得到7个圆弧截面。

3.2 绘制二维翼型

在上述7个平面截面处建立草图，由计算得到的翼型坐标来绘制二维平面翼型。具体绘制步骤如下：

以草图原点为起点水平绘制弦长。分别以弦长两端端点为圆心，翼型中线半径为半径画圆。两圆相交于两点，以下交点为圆心，翼型中线半径为半径画圆，弦长截到的劣弧为翼型中线。

图4 等分翼型中线Fig.4 Equal division of airfoil center-line

用智能尺寸测量弦长两端的翼型中线半径间的弯曲角。对翼型中线半径进行圆周阵列，跨距为弯曲角，如图4所示。由图4中可以看出，弯曲角为34.57°，阵列数量根据不同标准叶型的占比不同，进行不同程度的等分，如NACA-65翼型，占比多数为5%，因此将弯曲角等分为20等分。

延长等分线绘制构造线，在构造线上截取y坐标值长度，得到翼型吸力面和压力面轮廓各点。将得到的吸力面和压力面各点利用样条曲线依次连接成曲线，形成二维平面翼型，如图5所示。图5中虚线轮廓为轮毂截面二维平面翼型。根据安装角对翼型进行调整，得到各截面二维平面翼型，实线轮廓为经过调整后的轮毂截面二维平面翼型。

图5 轮毂截面二维平面翼型Fig.5 Two-dimensional airfoil in hub section

对形成的二维平面翼型进行评估可得到基体的重心位置的x、y坐标，根据得到的重心坐标调整草图的二维平面翼型位置，使重心位于草图原点，将各截面二维平面翼型重心在基准轴上积叠。

3.3 叶片三维造型

利用“包覆”指令将各二维平面翼型弯曲到对应的圆弧截面上。对在圆弧截面上形成的弯曲后的三维轮廓曲线进行“曲面拉伸”，依次选择弯曲后的轮廓曲线，使各截面的轮廓曲线拟合成曲面得到三维扭曲叶片造型，如图6所示。

图6 动叶三维造型Fig.6 Three-dimensional modeling of rotor

利用Solidworks中的“包覆”指令实现将二维平面翼型转化为圆弧截面上的三维轮廓曲线，建立准确的动叶三维造型。

4 结语

对动调轴流风机叶片三维造型设计方法进行了介绍，采用Solidworks包覆功能法建立叶片三维实体模型，并将该方法形成的三维轮廓曲线进行叶片截面弯曲理论验证，验证结果表明，忽略数据计算误差情况下，包覆法形成的三维轮廓曲线完全还原理论计算值。该造型方法提高了叶片三维造型的准确度，减小叶片三维造型与理论计算的误差，为后续气动分析奠定理论基础，并为各类轴流压气机的叶片造型提供参考。