汽轮机叶型几何特性及机械特性研究
余 锐,竺晓程,沈 昕,周代伟,阳 虹,杜朝辉
(1.上海交通大学,上海 200240;2.上海电气电站设备有限公司汽轮机厂,上海 200240)
叶片设计是汽轮机、燃气轮机等设计的重要环节,直接影响叶片的效率以及整个机组的性能表现。设计成形的叶片各截面型线包含了叶型的重要信息,如叶型弦长、最大厚度、进出口几何角、安装角等几何特性[1],以及叶型的面积、重心、惯性矩、抗弯模量等机械特性[2]。这些是叶片气动特性、叶片强度以及振动计算的原始数据,其精度会直接影响到叶片气动特性、叶片应力以及频率计算的准确性。因而对以上参数的计算方法既要求简单易行,又要求具有足够的精度。由于叶型几何形状复杂且叶型数据来源众多,既可以由多项式曲线、Bézier 曲线及B 样条曲线等连续曲线定义,也可以由一系列离散点数据定义(尤其是在借鉴引进技术的叶型资料时)[3]。不过无论是何种形式定义的叶型,根据型线数据逆向求解叶型的几何特性及机械特性参数都具有重要意义。因此,本文基于原始叶型型线的数据对原叶型的设计信息进行逆向工程研究,获取叶型设计中关键的几何及机械特性参数,为叶型的修改优化以及新叶型的开发奠定基础。
1 叶型定义及几何参数
如图1 所示,本文研究的叶型是由两段参数化Bézier 曲线定义得到的,叶型尾缘开口未封闭。根据叶型型线的定义,采用连续密集坐标点描述叶型,可以将其视作叶片型线的离散形式。
在计算叶型机械特性参数时,仅要求数据坐标点按顺时针方向排序且叶片前缘在尾缘的左侧,而对起始点的位置无要求,可以从叶片上任何位置开始。

图1 基于贝塞尔曲线描述的叶型
基于上述叶型描述方式,对于本文研究所涉及的叶型及叶栅几何参数主要分为两类:(1)由叶型、叶栅几何外形决定的参数:中弧线、叶片弦长、安装角、最大厚度、通道收敛性、喉部特性、几何进出气角及前缘、尾缘小圆等;(2)由前一特性得到的相关衍生参数:折转角、最大厚度对应内、背弧上的点、最小通道尺寸等。
其中通道收敛性、最大厚度、喉部特性均与求解两曲线间公切圆相关,而叶片弦长、叶片安装角则与曲线公切线求解相关。因此,本文主要介绍曲线公切线及公切圆的求解方法,以此为基础可完成以上所有参数的求解。
2 叶型压力面公切线求解
首先定义平面曲线p(u)=[x(u),y(u)]的相对曲率:

如图2 所示,下面介绍本文求解叶型压力面处公切线的方法:
1)首先在叶片压力面上找到弯曲方向变化的两点O1、O2,则公切线切点分别在O1、O2点两侧;
2)用两分法寻找公切线,在图中O1靠近叶片前缘上找控制点A1,过该控制点的切线为;在O2靠近叶片尾缘上找控制点C2,过该控制点的切线为使得切线:
这样就可求得叶型压力面处的公切线以及对应的切点,进而可求得与之相关的叶型几何参数,如弦长、安装角等。

图2 叶型压力面处公切线
3 曲线间公切圆求解
根据叶型中弧线的定义:中弧线是通过叶型所有内切圆圆心的连线,是一个重要的叶型几何参数。求解叶型的中弧线即求解叶型压力面和吸力面一系列内切圆的圆心[4],另外叶栅通道特性及喉部特性的求解也可归结为求解构成叶栅通道的两型线间的公切圆圆心。在此以叶型中弧线求解为例,采用直接法求解曲线间的公切圆。
直接法求解公切圆圆心的步骤如下:
1)如图3(a)所示,在吸力面上A1点沿其法线做射线A1C1,其中A1C1与压力面或吸力面(或其延长线上)交于C1点,如果A1C1与压力面或吸力面均无交点(从压力面与吸力面未连接一段空隙射出),则给定C1点x 坐标同吸力面端点x 坐标值;
2)此时过吸力面A 点与吸力面和压力面的公切圆圆心在A1与C1点之间;
3)在线段A1C1上寻找公切圆圆心:
①C1点在压力面上,其中C1P1为压力面在C1点上的切线,如图3(a)所示:
a.当∠A1C1P1>90°,则在压力面C1P1反向上找B1点(u1=uC1,u2=uled),否则在C1P1方向寻找B1点(u1=uC1,u2=1);
b.B1点寻找方式按照两分法,当D1E1>A1E1时u2=uD1,否则u1=uD1。
②C1点在吸力面或与吸力面、压力面均无交点,此时u1=uled,u2=1 。如图3(b)所示:
当D1E1>A1E1时u1=uD1(如图3(c)所示),否则u2=uD1(如图3(d)所示)。
按照上述曲线间公切圆的求解方法,可以求出叶型的中弧线,根据中弧线端点处的切线方向就可以求得叶型的几何进出气角;同时可确定叶型最大厚度及位置,以及叶栅通道特性等参数,如图4 所示。


图3 直接法求解公切圆圆心

图4 叶栅通道特性示意图
需要注意的是,本文的叶型是由两条Bézier曲线组成,虽然在前缘处连接,但此连接点并不一定是叶型的前缘点,因此需要作出进一步的判断。从叶型前缘连接点处开始,若叶型压力面和吸力面型线的曲率变化均单调递减,说明在连接点处曲率最大,则该点为前缘点;若非单调递减情况,则找出两型线在前缘附近曲率最大的一点,即为所要寻找的前缘点。
尾缘处由于未封闭,根据曲线间公切圆求解原理,可以求出与叶型压力面、吸力面以及尾缘处控制点连线的公切圆,即尾缘小圆。中弧线尾缘处切线与小圆的交点即为叶型尾缘点。
4 叶型机械特性计算
根据叶型定义可以离散出足够多的连续坐标点,因此相邻两点之间可以采用直线段的连接形式去计算积分,按照文献[2]中针对叶型面积、惯性矩以及高次矩等机械特性的理论计算方法,可以求出相应的机械特性参数,为强度及振动计算提供必要信息。
计算时为避免由于直线斜率为无穷大,导致数值计算时引起计算机处理出现上溢或下溢问题,对数据采取了积累弦长参数化法处理。图5给出了根据叶型数据计算叶型几何特性和机械特性参数的流程图。
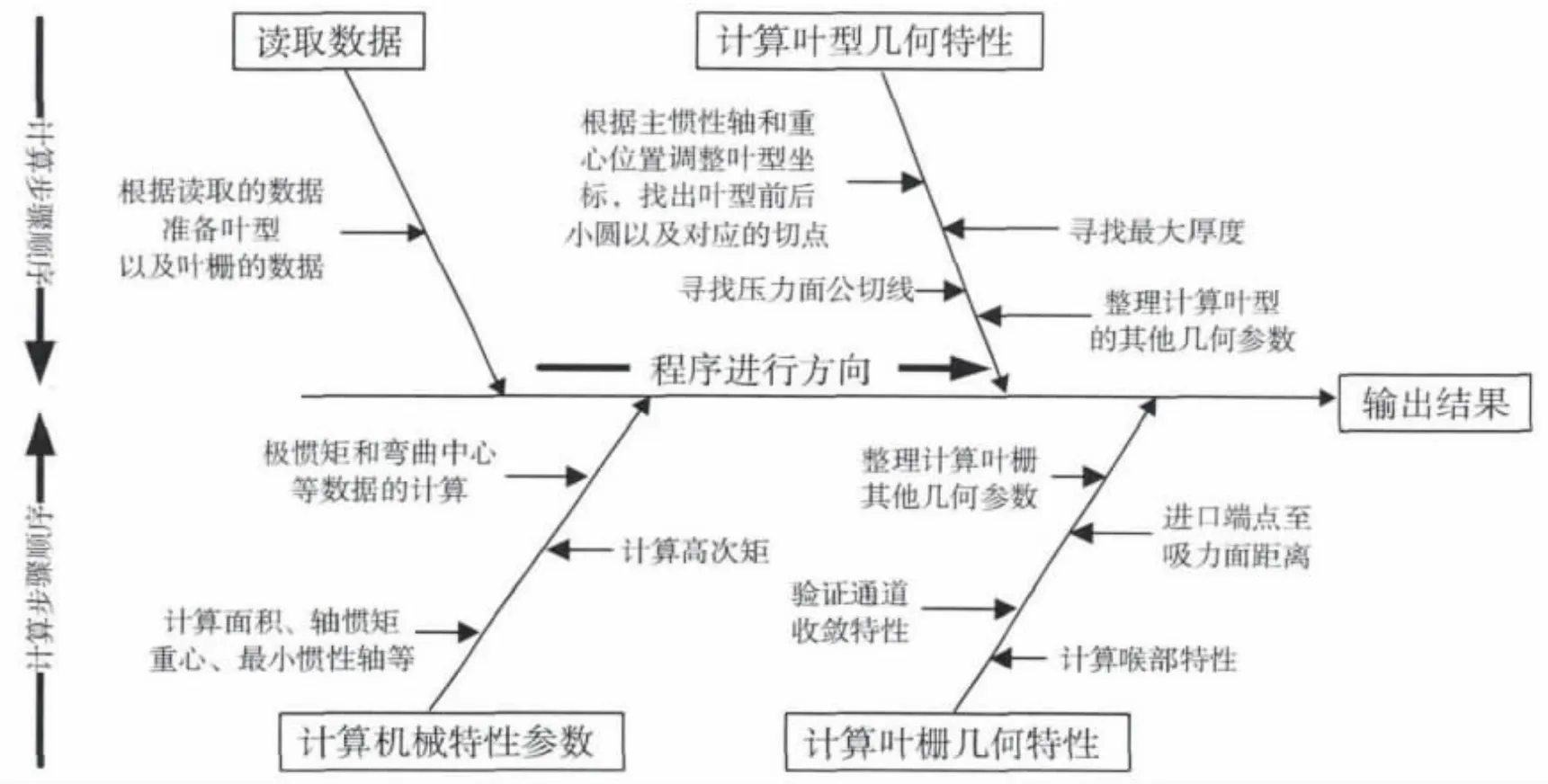
图5 叶型几何和机械特性计算
5 结论
本文详细介绍了曲线间公切线以及公切圆的求解方法,以此为基础研究某Bézier 曲线定义的叶型,对其中弧线、最大厚度、安装角以及叶栅的通道特性等几何特性参数进行计算,并采用参数化的方法求解叶型的机械特性参数,建立起一套完整的叶型几何及机械特性计算方法,为叶型进一步的改型设计和再开发奠定了重要的基础。
[1]周岳琨,王建新,管继伟,等.汽轮机叶片设计和几何成型方法综述[J].汽轮机技术,2001,43(4):198-202.
[2]丁有宇.汽轮机强度计算手册[M].北京:中国电力出版社,2010.
[3]徐旭岭,丁旭东,隋永枫,等.汽轮机叶型的数字化及几何信息采集[C]// 2009年学术研讨会论文集.北京:中国动力工程学会透平专业委员会,2009.
[4]陆启超.中弧线的计算问题[J].数学的实践与认识,1979(4):24-35.

