有限元单元类型对汽轮机长叶片应力计算的影响

谈尚炯，程 凯，顾璐寅，刘 岩

(1.上海汽轮机厂有限公司，上海 200240;2.上海电气电站设备有限公司，上海 200240)

在使用商业有限元软件进行长叶片应力计算的过程中，网格划分是重要的组成部分，网格的质量与单元类型直接影响到计算结果的精确性。在长叶片应力计算的前处理中，已经形成了较为规范化的网格划分方法，即尽量采用线性八节点六面体单元对叶片大部分规则区域划分结构化网格，在非规则区域辅以少量四面体与五面体非结构网格，以保证网格的合理过渡与整体质量。但是，在实际的长叶片有限元计算中发现，不同的网格单元类型也会导致计算结果的差异，尤其是分别使用完全积分单元、减缩积分单元与非协调单元时，应力差异最大可达30%以上，甚至跨越屈服极限。这说明，这三种单元类型在计算所得的应力中，存在不符合实际情况的结果。所以，对这三种网格类型进行深入分析，找出究竟何种网格类型适用于长叶片的应力计算，这对提高长叶片应力结果的精确性有较大的工程意义。

1 研究问题描述

完全积分单元，是指当单元具有规则形状时，所用的高斯积分点的数目足以对单元刚度矩阵中的多项式进行精确积分［1］。但是，当承受弯曲载荷时，线性完全积分单元会出现剪切闭锁问题，造成单元过于刚硬。剪切闭锁的原理如图1 所示。发生剪切闭锁时，即使网格划分很细，计算精度仍然很差。

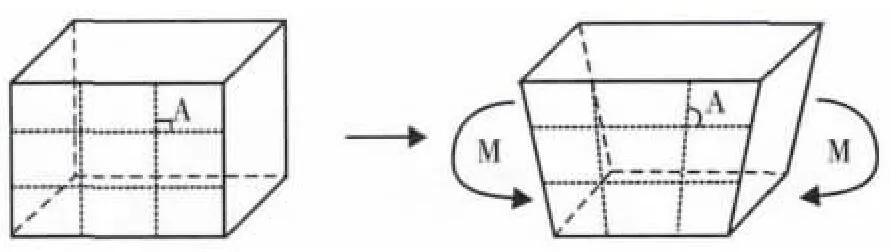
图1 完全积分单元在弯矩作用下的变形示意图［3］

相反，减缩积分单元可以避免剪切闭锁问题的发生。减缩积分单元是在普通的完全积分单元的基础上在每个方向减少一个积分点，这种单元形式大大减小了刚度矩阵的规模，节约了计算时间。但是由于减缩积分单元的积分点位于单元的中心，单元的变形不会引起积分点处应变能的产生，实际出现的单元变形模式像沙漏的形状，称为沙漏模式［1］。沙漏模式的原理见图2，沙漏模式下的结构表现得非常柔软，在应力结果上与真实情况相差很大，并且会导致不真实低频模态的出现。

图2 减缩积分单元在弯矩作用下的变形示意图［3］

非协调单元也可以纠正完全积分单元出现的剪切闭锁问题。非协调单元将增强单元变形梯度的附加自由度引入到线性单元中，以避免单元交界处的位移场出现重叠或裂痕。但是如果单元形状较差，非协调单元的分析精度就会下降。如果所关心部位的单元扭曲较大，尤其是出现交错扭曲，分析精度就会受到严重影响。

综上所述，剪切闭锁与沙漏模式是一对矛盾，想同时消除剪切闭锁与沙漏模式是不可能的。上述三种单元类型没有绝对的优劣之分，我们要做的只是针对不同的应力状态选择合适的单元类型，既要避免大面积的剪切闭锁问题，也要限制沙漏模式的发生。

文献［3-7］中缓解与克服剪切闭锁问题的方法有:

1)使用减缩积分单元，但是减缩积分单元会导致沙漏模式的产生。

2)使用二阶完全积分单元，但是使用这种单元无法进行接触分析。对于长叶片结构，计算模型涉及叶根与叶根槽的接触，以及围带的接触等。而且，使用二阶单元，会大大增加计算量，从而提高叶片设计开发的成本。

3)使用细化的网格。一方面，这只能缓解剪切闭锁问题的发生，而不能从根本上解决问题;另一方面，在长叶片的有限元计算过程中，为了控制计算规模，网格数量会受到限制，因而单元尺寸不可能任意缩小。

限制沙漏模式的方法有:

1)使用完全积分单元，但是完全积分网格会导致剪切闭锁问题的产生。

2)使用二阶减缩积分单元，同样，这种单元类型也无法用于网格接触分析，显然不适用于长叶片的分析过程。

3)使用细化的网格。同样，这无法从根本上解决问题，且为了控制计算规模，这种方法可行性不强。

另外，文献中还提到可以通过添加自由度或添加人工刚度等方式来抑制沙漏模式的出现。但是这不是我们目前阶段的研究重点。我们的目标是针对长叶片的结构与实际受力状态，找出适合长叶片有限元计算的单元类型。

为了研究上述问题，我们选用变截面扭转的某汽轮机长叶片为原型，并进行了简化，以排除网格质量对计算结果的影响。在同一套网格下使用不同的单元类型，计算该叶片在离心力载荷与汽流力作用下的应力分布。

2 有限元模型

本文采用某产品叶片为母型，建立简化模型进行分析。为了保留叶片型线的扭转与渐缩对叶身内部应力分布的作用，并排除网格质量对计算结果的影响，将叶片简化为如图3(a)所示的扭转减缩体。图中，叶型部分高度为2 000 mm，仅取母型叶片的底部截面与顶部截面的外切矩形，其余部分由几何线性插值获得。简化后，顶部截面与底部截面的面积比为0.165，主惯性轴夹角为58.5°。

叶根部分由中间体截面向下拉伸而成。简化模型忽略了原有叶型的围带部分，在后续的计算中，只考虑单个自由叶片在运行过程中的应力分布。网格划分时，对整个叶片全部使用六面体网格，节点数为11 915，单元数为9 528，如图3(b)所示。网格划分完成后，对网格单元分别赋予一阶完全积分单元、一阶减缩积分单元与一阶非协调单元的单元类型。

本文采用非线性有限元软件ABAQUS 对该叶片的稳态应力进行分析求解。为了更精确地模拟叶片在工作过程中受到的弯力，在有限元模型中，除1 500 r/min 的离心力载荷外，还将CFD 中计算得到的汽流力等效加载到叶身表面。

图3 叶片简化模型几何与网格示意图

3 结果分析

首先考察叶片整体的应力分布，图4 至图6分别给出完全积分单元、减缩积分单元和非协调单元三种情况下的叶片应力分布云图。

图4 完全积分单元的应力云图

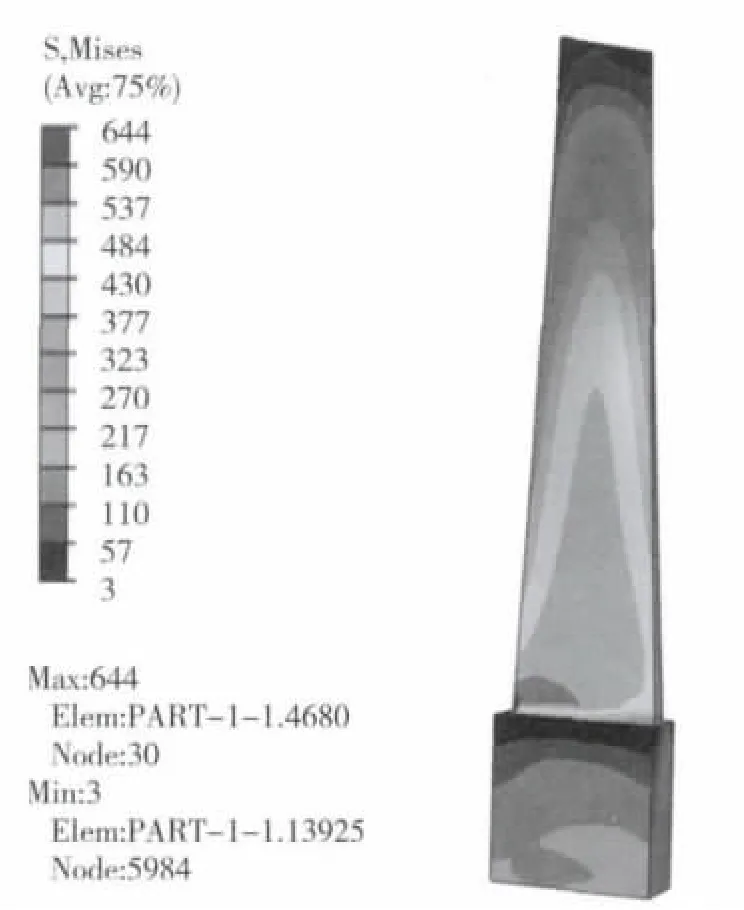
图5 减缩积分单元的应力云图

图6 非协调单元的应力云图

由图4 至图6 可以看出:

1)三种网格单元类型下计算所得的应力场分布趋势基本相似，无论选择哪一种单元进行计算，所得到的叶片受力定性规律是相同的;

2)应力在叶型的根部表现出相对较大的应力集中，三种网格单元类型的计算结果都显示应力最大值出现在叶型底部出汽边位置;

3)完全积分单元所得的应力极值最大，达到749 MPa;减缩积分单元所得的应力极值最小，为644 MPa，仅为完全积分单元计算结果的86%;非协调单元所得的最大应力值为672 MPa，介于两者之间。

沿该叶片的出汽边取52 个点(参见图7)，输出其应力值与位移值，如图8 与图9 所示。首先，从叶片出汽边沿叶高方向的应力分布来看，沿着叶高应力呈逐渐减小的趋势，这是因为沿着叶高的每个截面承受的离心力载荷逐渐减小;其次，变形量的主要成分是离心力导致的扭转恢复角，变形量沿着叶高方向逐渐增大的趋势也符合叶身扭转的真实情况，当然由于该简化模型是对原有模型的定性描述，与真实叶片的计算结果会有一定差距。

对比三种网格单元类型下的应力计算结果，可以发现:

1)三种单元类型的计算结果表现出一致的趋势，总体来说，完全积分单元的应力结果较大，而减缩积分单元与非协调单元的计算结果较小。

图7 叶片出汽边的52 个应力和位移量考察点

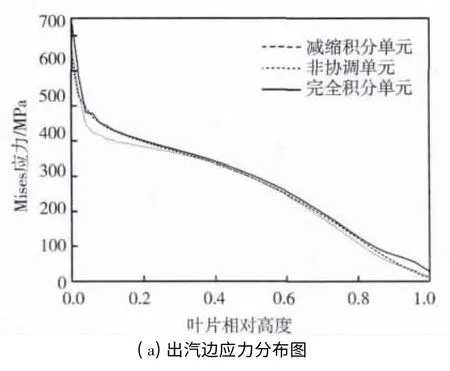
图8 沿叶片出汽边的应力分布图

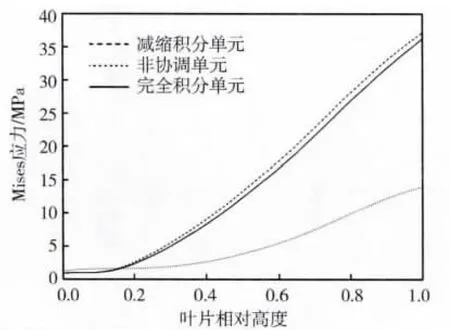
图9 沿叶片出汽边的位移量分布图

2)靠近叶型根部与顶部位置，三种单元类型的计算结果表现出一定的差异，其中，在根部附近位置，完全积分单元计算得到的应力最高，而非协调单元计算得到的应力最低;在叶型顶部位置，完全积分单元计算得到的应力最高，而减缩积分单元计算得到的应力最低。

对比三种网格单元类型下的位移计算结果，可以发现:

1)三种单元类型的计算结果表现了一致的趋势，沿着叶高方向变形量逐渐增大;

2)沿着叶高方向，完全积分单元计算得到的位移量始终小于减缩积分;

3)非协调单元计算得到的位移量呈现出与其他两种单元的计算结果比较大的差距。

根据三种网格单元类型的特性，对可能导致产生上述现象的原因作出如下推测:

1)减缩积分单元的计算结果出现了一定程度的沙漏现象。查看计算过程中伪应变能与内能，发现伪应变能仅占内能的0.23%。根据文献［2］，当伪应变能占内能的比例低于1%时，沙漏模式对计算结果的影响不大。由此可见，本文算例中的沙漏模式对计算结果的影响很小。

2)完全积分单元的计算结果出现了一定程度的剪切闭锁现象。由于我们在本文模型的计算过程中考虑了汽流弯力的作用，而完全积分单元的位移场不能模拟由于弯曲而引起的剪切变形与弯曲变形。另外，相比于减缩积分单元的位移计算结果，完全积分单元的结果偏大，这正是剪切闭锁可能导致的现象。

3)非协调单元的位移计算结果与其他两种单元类型的结果有较大差异。推测原因为:对于本文中的模型，叶型受到离心力后的扭转恢复角较大，以至于产生了网格的平行扭曲，这会大大降低非协调单元的计算精度。

4 结论

对于汽轮机长叶片而言，影响有限元计算结果准确性的因素很多，本文从单元类型的角度进行分析，分别使用一阶线性的完全积分单元、非协调单元以及减缩积分单元对简化的叶片模型进行结构分析。分析结果显示，减缩积分单元能较好地分析长叶片的受力状态，在网格质量保证的情况下，沙漏模式的影响非常小;完全积分单元对于受弯力作用的长叶片可能出现比较明显的剪切闭锁现象;而非协调单元对网格质量比较敏感，在网格出现平行扭曲或交错扭曲的情况下，计算精度会大幅下降。在对本文中的叶片简化模型进行应力计算的过程中，综合考虑计算规模和计算精度，减缩积分单元应当是可选用的适用性较好的单元类型。但对于造型复杂的真实叶片，其应力计算结果受到网格质量与单元类型的共同作用，难以单独考察单元类型对计算结果的影响，因而如何选择单元类型有待进一步研究。

［1］石亦平，周玉蓉.ABAQUS 有限元分析实例详解［M］.北京:机械工业出版社，2006.

［2］曹金凤，石亦平.ABAQUS 有限元分析常见问题解答［M］.北京:机械工业出版社，2009.

［3］包刚强，ERKE Wang，郝清亮，张国兵.对主流有限元软件控制剪切自锁和沙漏模式的比较和研究［C］//第八届中国CAE 工程分析技术年会论文集.成都:第八届中国CAE 工程分析技术年会，2012:517-524.

［4］张汶艳，祁顶春.浅谈ABAQUS 单元选择［C］//河南省汽车工程学会第五届科研学术研讨会论文集.郑州:河南省汽车工程学会，2009:174-175.

［5］张利民，王克明，吴志广.叶片模态分析的单元类型选择［J］.沈阳航空航天大学学报，2011，28(2):21-24.

［6］郭建生.有限元方法中单元类型和密度对计算结果的影响［J］.湖北工业大学学报，2007，22(4):25-28.

［7］DUCHATEAUG，BERGEAUD V，GAIFFE S，SCHEURER B.Control of Hourglass Modes in Prisms with Pentagons or Hexagons As Bases［J］.Finite Element in Analysis and Design，2006(42):1199-1210.