关于欧拉方程解的研究

常秀芳

（山西大同大学数学与统计学院，山西大同037009）

变系数的线性微分方程的求解一般没有固定方法可循，然而现实生活中常常遇到诸如热传导、振动谐波、电磁波、等变系数的线性微分方程问题，它们正好是特殊的变系数的线性微分方程——欧拉方程[1-4]。

1 概念

定义形如

的方程，称为欧拉方程。其中：p1,p2,…,pn-1,pn是常 数且p1≠0, 当f(x)≡0 时 ，方 程xny(n)+p1xn-1xy(n-1)+… +pn-1xy′+pny=0 称为n阶线性齐次欧拉方程。

当f(x)≠0 时，方程xny(n)+p1xn-1y(n-1)x+…+pn-1xy′+pny=f(x)

称为n阶线性非齐次欧拉方程。

欧拉方程用微分算子表示为

由解的结构知：只要能求得n阶线性齐次欧拉的通解以及n阶线性非齐次欧拉方程一个特解，则欧拉方程的通解即可写出。至于特解的形式可参阅n阶常系数线性微分方程的特解形式进行假设，用代入法求得，或知齐次方程的通解用常数变易法解之，因此，关键是求n阶线性齐次欧拉的通解。

2 特点

欧拉方程是一个n阶变系数线性微分方程，其特点：（1）它的左边的每一项是都由幂函数与未知函数导数的乘积组成；（2）每一项幂函数的指数与未知函数导数的阶数相等；（3）k阶导数Dky的系数是k次的幂函数pn-kxk(k=0,1,2,…,n，且P0=1)。

3 一般解法

当n=1时，是一阶欧拉方程

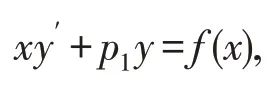
变形为

则此方程为一阶线性微分方程，其通解是

当n≠1时，设x=eu，因

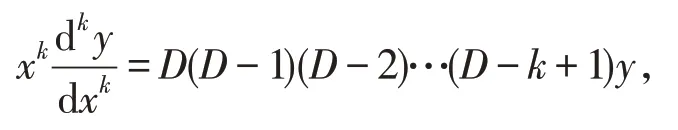
将上述各项代入方程

得一个关于未知函数是y，自变量为u的常系数线性方程

Pn(D)y=0，

求得此常系数线性齐次方程后，因x=eu，所以用u=lnx回代，则得齐次欧拉的解。

例1求方程x3y‴+3x2y″+xy′-y=xlnx的解。

解设x=eu，因原方程为

[D(D-1)(D-2)+3D(D-1)+D-1]y=ueu，即

(D3-1)y=ueu，

其特征方程为r3-1=0，特征根为

则(D3-1)y=0 的通解为

设方程 (D3-1)y=ueu的特解为y∗=u(Au+B)eu，代入方程得

(6Au+6A+3B)eu=ueu，

因此方程(D3-1)y=ueu的通解为

则所求方程的通解为

4 独特解法

由幂函数导数仍为幂函数的特点，不妨设欧拉方程

代入原方程为

由于xλ≠0，则得一个关于λ的n次一元方程

不妨规定此方程为欧拉方程的特征方程。

4.1 特征方程有n个不同的特征根

设欧拉方程的特征方程有n个不同的特征根为λ1,λ2,…,λn。

因λ=λ1,λ2,…,λn而 且λ1,λ2,…,λn互 不 相等，于是xλ1,xλ2,…,xλn线性无关。则欧拉方程的通解为

解特征方程λ(λ-1)+λ-1=0 ，特征根为λ=±1，所以，所求方程的通解为

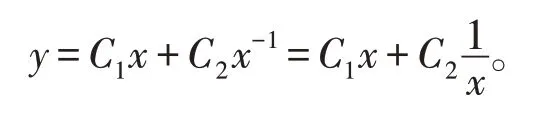
4.2 特征方程有两个同的特征根

设欧拉方程的特征方程有两n个相同的特征根为λ1、λ2。

因λ=λ1=λ2，所以y1=xλ1是齐次欧拉方程的解。

设y2=xλ1lnx，因

由于λ1是特征方程的重根，将代入齐次欧拉方程的左端，化简得

因此，y2=xλ1lnx也是齐次欧拉方程的解。又y=xλ1与y=xλ1

lnx线性无关，所以欧拉方程的通解含有 (C1+C2lnx)xλ1项。

例3求方程x2y″-xy′+y=0 的通解。

综合考虑研究区6个时相遥感影像，决定在NDVI概率累计表上取概率为99.5%的值为NDVImax，取概率为0.5%的为NDVImin，并利用ERDAS IMAGINE 2013 软件中的Modeler实现植被覆盖度定量转换模型，得到1989—2015年6期植被覆盖度专题图。

解特征方程λ(λ-1)-λ+1=0，即(λ-1)2=0特征根为λ=1 ，所以，所求方程的通解为y=(C1+C2lnx)x。

4.3 特征方程有共轭复数的特征根

设欧拉方程的特征方程有一对的共轭复数的特征根为α±iβ。

因λ=α±iβ，则是欧拉方程的解。

由欧拉公式知

由线性齐次微分方程解的结构知：

又y1与y2线性无关，所以齐次欧拉方程的通解含有xα[C1cos(βlnx)+C2sin(βlnx)]项。

例4求方程x2y″+xy′+y=0 的通解。

解特征方程λ(λ-1)+λ+1=0，即λ2+1=0，

特征根为λ=±i，所以，所求方程的通解为y=C1cos(lnx)+C2sin(lnx)。

4.4 特征方程有k重共扼复数的特征根

若λ=α±iβ是欧拉方程的k重共轭复数的特征根，则欧拉方程的通解一定含有

5 求齐次欧拉方程通解的具体步骤

第一步：依据方程写出特征方程

第二步：求出特征根；

第三步：依特征根写出方程的通解如表1。

表1 齐次欧拉方程特征根与通解关系的对照表