SCARA并联机构刚度和动力学分析
朱 伟 郭 倩 马致远 沈惠平 吴广磊
(1.常州大学机械工程学院, 常州 213016; 2.大连理工大学机械工程学院, 大连 116024)
0 引言
SCARA型并联机构具有三平移一转动运动输出特征,由于具有速度快、精度高、操作性能好等优点,受到国内外学者的广泛关注,该型机械手对于完成装配、包装、抓拿及码垛等高速重复性工作具有独特优势[1]。
文献[2-5]先后发明了一类由4条R-(SS)2支链(其中R表示转动副,S表示球副)和双平台组成的SCARA型高速并联机械手,分别称H4、I4、Par4和Heli4。黄田等[6]在H4机构的基础上,设计了一种支链为2-(2-R(SS)2)R的三平移一转动并联机构,用于生产线中高速搬运,称为Cross—IV型机器人。刘辛军等[7]采用4条相同支链R-(SRS)2-R,得到一种单平台SCARA并联机构——X4,并通过尺寸性能优化,实现了较大角度的转动输出。沈惠平等[8-9]基于方位特征(POC)理论和机构结构降耦原理,设计了一类非对称低耦合度能实现三平移一转动(3T1R)的SCARA并联操作手机构。
机构刚度是描述并联机构抵抗变形能力的重要指标,分析方法有虚拟关节法和虚拟弹簧法。如文献[10-11]根据虚拟关节法,建立支链末端刚度矩阵,进而建立机构的近似整机静刚度解析模型。这种方法应用较广泛,在关节中添加虚拟关节,极大简化了模型,但没有考虑机构空间六自由度的刚度耦合。WU等[12]利用虚拟弹簧方法,对Ragnar和Quattro机器人进行刚度建模,通过对机构末端的笛卡尔刚度矩阵无量纲化,得到机构转动和移动两类刚度指标。这种方法可对支链单独建模,从而可较方便地得到机构的整体刚度性能。
本文提出一种可实现SCARA运动的四自由度高速并联机器人机构,由2条R(SRS)2R支链和2条RSS支链构成。分析机构的拓扑结构特征及运动学位置反解,根据虚拟弹簧法建立机构的笛卡尔刚度矩阵,引入2个无量纲化性能指标,分别评价机构的平移刚度和旋转刚度性能,并分析机构定位移和定姿态下的刚度分布;根据虚功原理方法建立机构的动力学方程,通过仿真验证动力学模型的正确性。
1 机构运动学分析
1.1 机构描述
机构的CAD模型如图1所示,由动平台、静平台及4条支链组成,原理图如图2所示。机构第1、2两支链为R(SRS)2R混合支链,记为HSOC{-Ri1-(Saj,Rej,Sbj,Scj,Rfj,Sdj)-Ri2-}(i=1,2;j=1,2)。(Saj,Rej,Sbj,Scj,Rfj,Sdj)为平行四边形闭合回路,记为(SRS)2,其中两转动副Rej和Rfj的轴线平行且垂直于(Saj,Sbj,Scj,Sdj)所在的平面。转动副Ri1轴线平行于球铰Saj和Sdj的连线,转动副Ri2轴线垂直于球铰Sbj和Scj的连线,且Ri1⊥Ri2。第3、4两支链为RSS支链,记为:SOC{-Ri1-Si2-Si3-}(i=3,4)。转动副R12、R22,球副S33、S43分别位于动平台上,R12和R22的轴线平行,且垂直于动平台平面;转动副R11、R21、R31、R41的轴线分别位于静平台的4条边,且R11∥R31,R21∥R41。
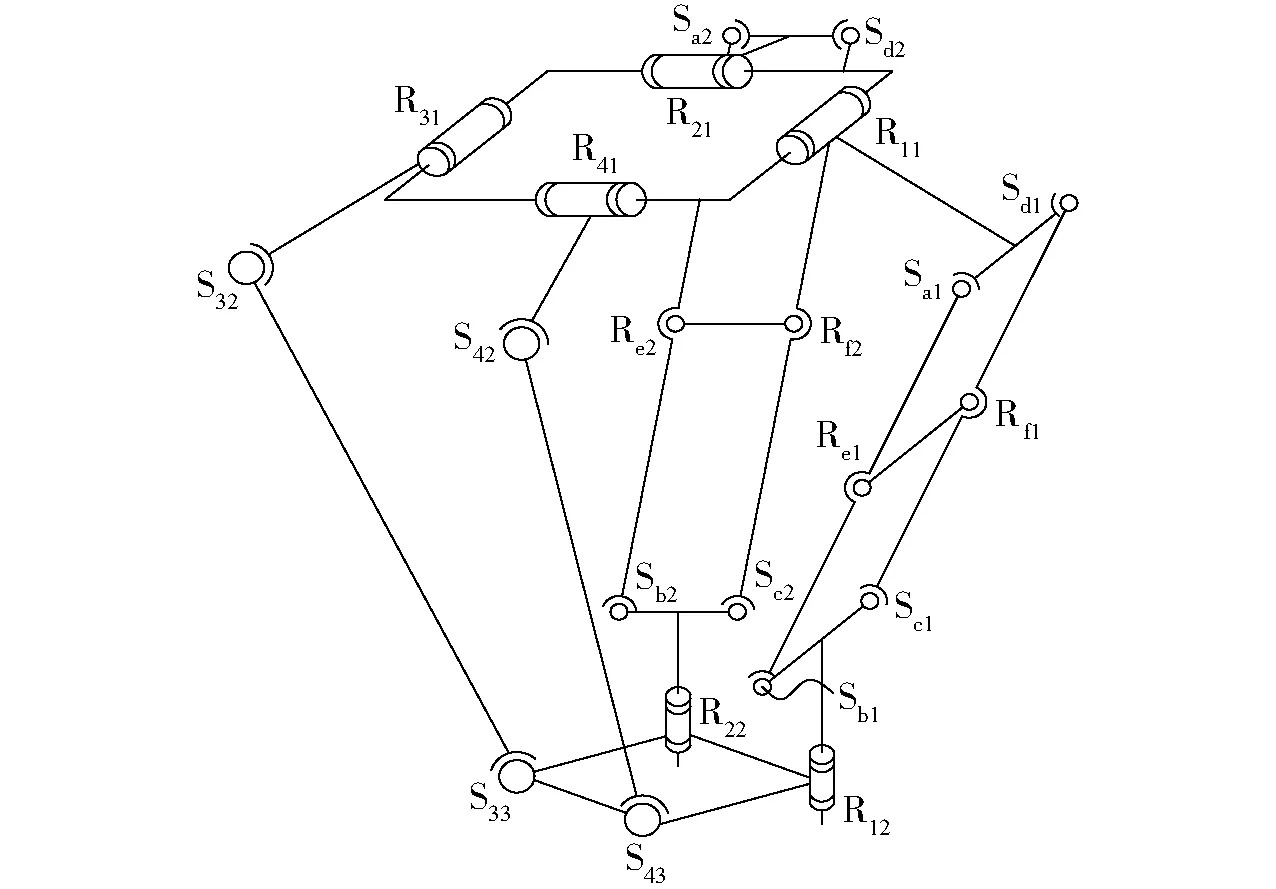
图2 机构原理图Fig.2 Mechanism schematic diagram
1.2 机构拓扑结构
两类支链末端构件的POC集[13]分别为
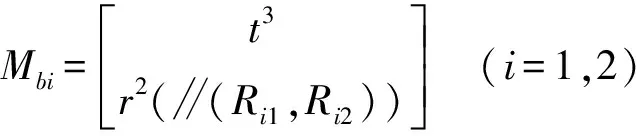
则机构动平台的POC集为
第1、2支链(i=1,2)构成的第1个独立回路的独立位移方程数ξL1为
由第1、2支链组成子并联机构和第3支链(i=3)构成的第2个独立回路的独立位移方程数ξL2为
由第1、2、3支链组成子并联机构和第4支链(i=4)构成的独立回路的独立位移方程数ξL3为
则机构自由度为
式中F——机构自由度
fi——第i个运动副自由度
ξLj——第j个独立回路的独立位移方程数
1.3 位置反解
为了便于分析,将机构模型等效为图3所示的结构简图。假设动、定平台均为正方形,在定平台的中心O点建立静笛卡尔坐标系Oxyz,x轴沿OA1方向,y轴沿OA2方向。设4条支链的主动臂AiCi与定平台夹角为θi(i=1,2,3,4),l1、l2、l3、e分别为主动臂AiCi、从动臂CiDi、CiBi、短杆DiBi的长度,OAi的长度为R,PBi的长度为r,在动平台的中心P点建立动笛卡尔坐标系Px′y′z′,x′轴沿PB1方向,y′轴沿PB2方向。
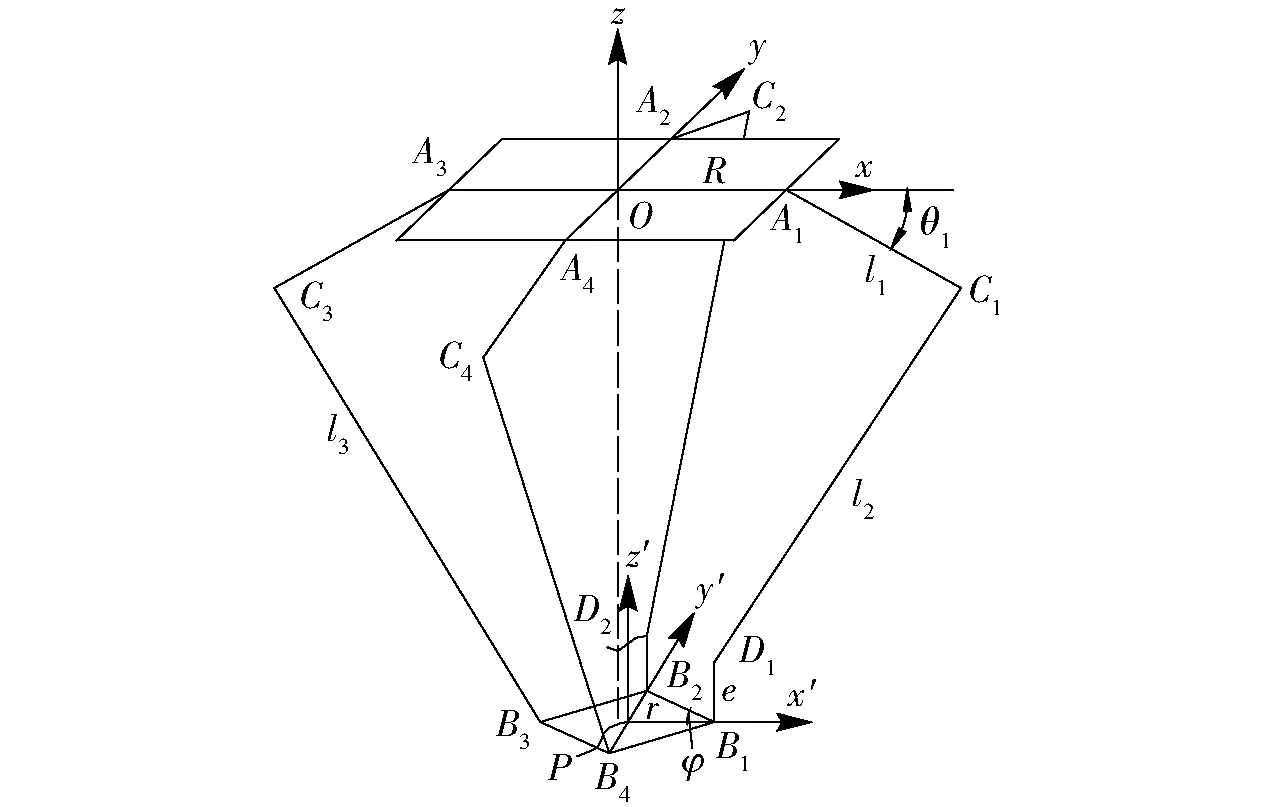
图3 结构简图Fig.3 Structure diagram
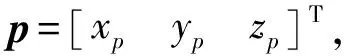
P点指向Bi点的矢量为
(1)
O点指向Ai点的矢量为
(2)
Di点指向Bi点的矢量为
(3)
主动臂AiCi的单位矢量为
(4)
其中
式中s为正弦函数,c为余弦函数。
由图3可知,各支链满足闭环矢量方程
p+si=ri+l1ui+l2vi+ei(i=1,2)
(5)
p+si=ri+l1ui+l3wi(i=3,4)
(6)
式中vi——从动臂CiDi的单位矢量
wi——从动臂CiBi的单位矢量
由式(5)和式(6)可得
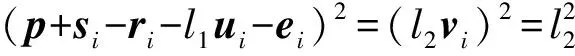
(7)
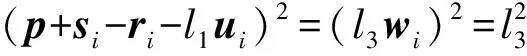
(8)
根据式(7)、(8),整理可得
Eisθi+Ficθi+Gi=0
(9)
其中E1=E2=2l1(p+si-ri-ei)T
E3=E4=2l1(p+si-ri)T
F1=F2=2l1(p+si-ri-ei)T(cαi+sαi)
F3=F4=2l1(p+si-ri)T(cαi+sαi)
依据机构装配模型,由式(9)解得机构的位置反解为
(10)
2 刚度分析
2.1 弹性静力学模型
并联机构的动、静平台相比支链连杆,具有更好的抗变形能力,故将其动、静平台视为纯刚体,机构整体刚度只和驱动及连杆刚度有关。根据虚拟弹簧法[14]理论,杆件的弹性变形可通过杆件末端的n-DOF(n表示自由度数)的虚拟弹簧表示,而杆件变形与受力的映射矩阵可由Euler-Bernoulli梁理论[15]得到。本机构由R-S-S无约束支链和R-(SRS)2-R混合支链组成,分别建立支链的虚拟刚度模型。
2.1.1R-S-S支链刚度模型
采用虚拟弹簧法建立R-S-S支链弹性静力学模型,如图4所示。
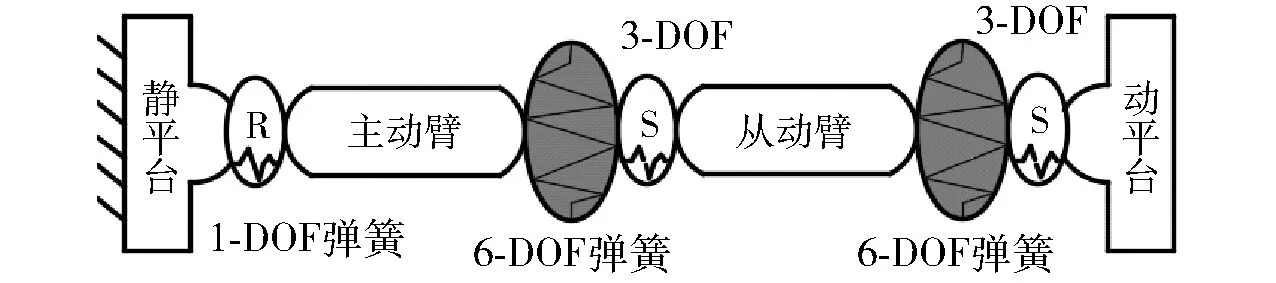
图4 R-S-S支链弹性静力学模型Fig.4 Elastic static model of R-S-S branch
图4中,1-DOF虚拟弹簧表示驱动关节R的伺服刚度,6-DOF虚拟弹簧描述机构中主动臂AiCi和从动臂CiBi(i=3,4)在空间中的弹性形变量,可分别用(Δd1,Δd2,…,Δd6)和(Δd7,Δd8,…,Δd12)表示,3-DOF的被动关节是考虑静力作用下球铰发生运动对支链刚度的影响,微小变形量可用(Δp1,Δp2,Δp3)表示。
在R-S-S支链中建立图5所示的局部笛卡尔坐标系C3x1y1z1和B3x2y2z2,x1轴沿A3C3方向;x2轴沿C3B3方向;y1轴和y2轴平行于中心为A3的转动副轴线方向,由于该支链直接连接动平台与静平台,故末端点直接选择动坐标系原点P。
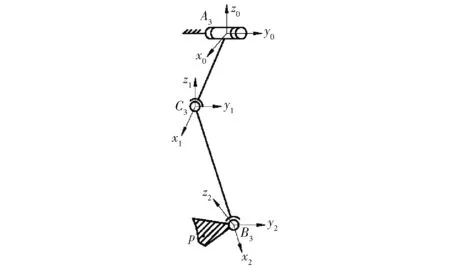
图5 R-S-S支链局部坐标系标注Fig.5 Local coordinate system labeling of R-S-S branch
利用螺旋理论,建立杆件变形和被动关节运动到末端的变形量ΔT,可表示为
(11)

(12)
式中 Δtr、Δtt——支链末端转动和移动变形量
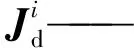
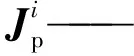
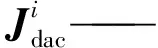
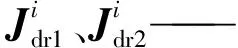
bi、ci——Bi、Ci在静坐标系的位置矢量
ui、ai、gi、wi、hi——x1、y1、z1、x2、z2局部坐标轴的方向矢量
其中
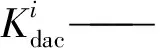
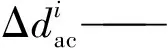
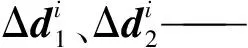
空间中单一连杆采用6×6的刚度矩阵来描述其刚度特性,记作kij,由Euler-Bernoulli[15]梁理论可得矩阵中每一项为
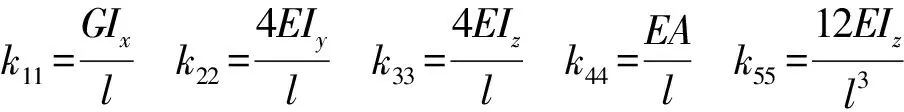
式中l——杆件长度
A——杆件截面积
Ix——杆件截面极惯性矩
Iy、Iz——截面惯性矩
E——材料弹性模量
G——材料切变模量
由文献[11]可知,静力平衡方程为
(13)
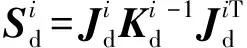
式中O3×3——零矩阵
由式(13)可得,支链刚度矩阵Ki为
(14)
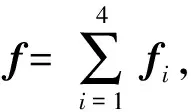
(15)
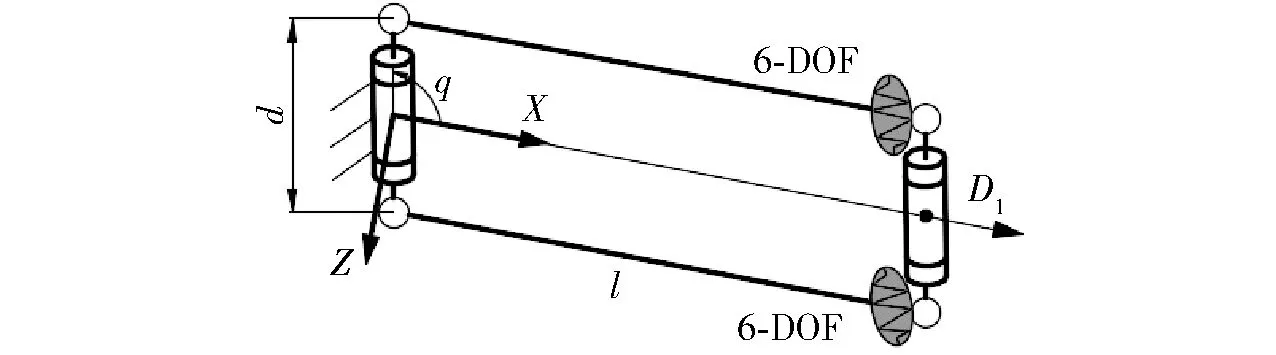
图6 平行四边形结构Fig.6 Parallelogram structure
2.1.2R-(SRS)2-R支链刚度模型
对于包含平行四边形结构的复杂支链,必须先将平行四边形结构作为独立结构进行刚度建模。根据文献[11]将(SRS)2结构运动特性简化为R-Pa-R(Pa为平行四边形)结构,并建立弹性静力学模型,如图6所示。
将两短边杆视作刚体,两长边杆视作悬臂梁,根据式(11)~(15),可得在局部坐标系中参考点D1处的刚度矩阵为
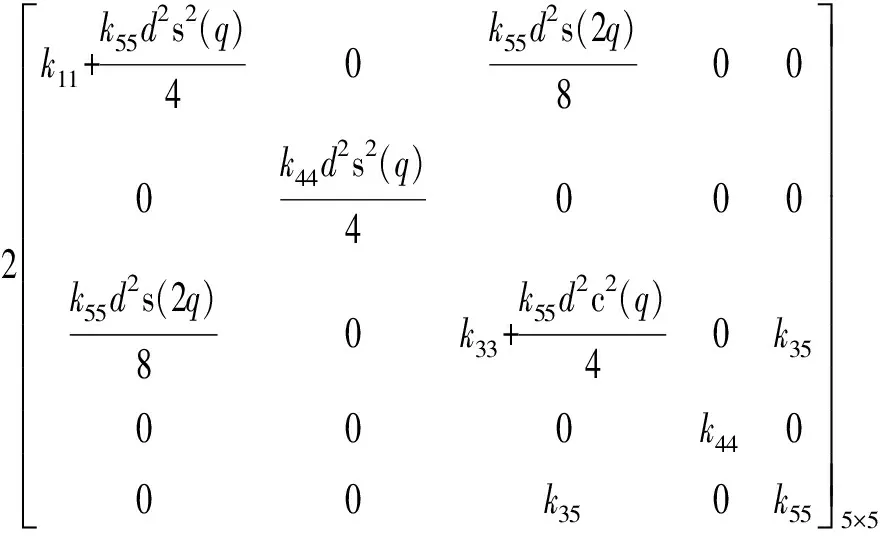
式中d——长度(图6)q——被动副转角
由于平行四边形末端点D1可绕局部坐标系Y(垂直于X、Z轴)轴转动,故没有沿Z轴方向的线性刚度,该支链末端以5自由度虚拟弹簧来描述其刚度特性。建立R-(SRS)2-R支链的弹性静力学模型如图7a所示。
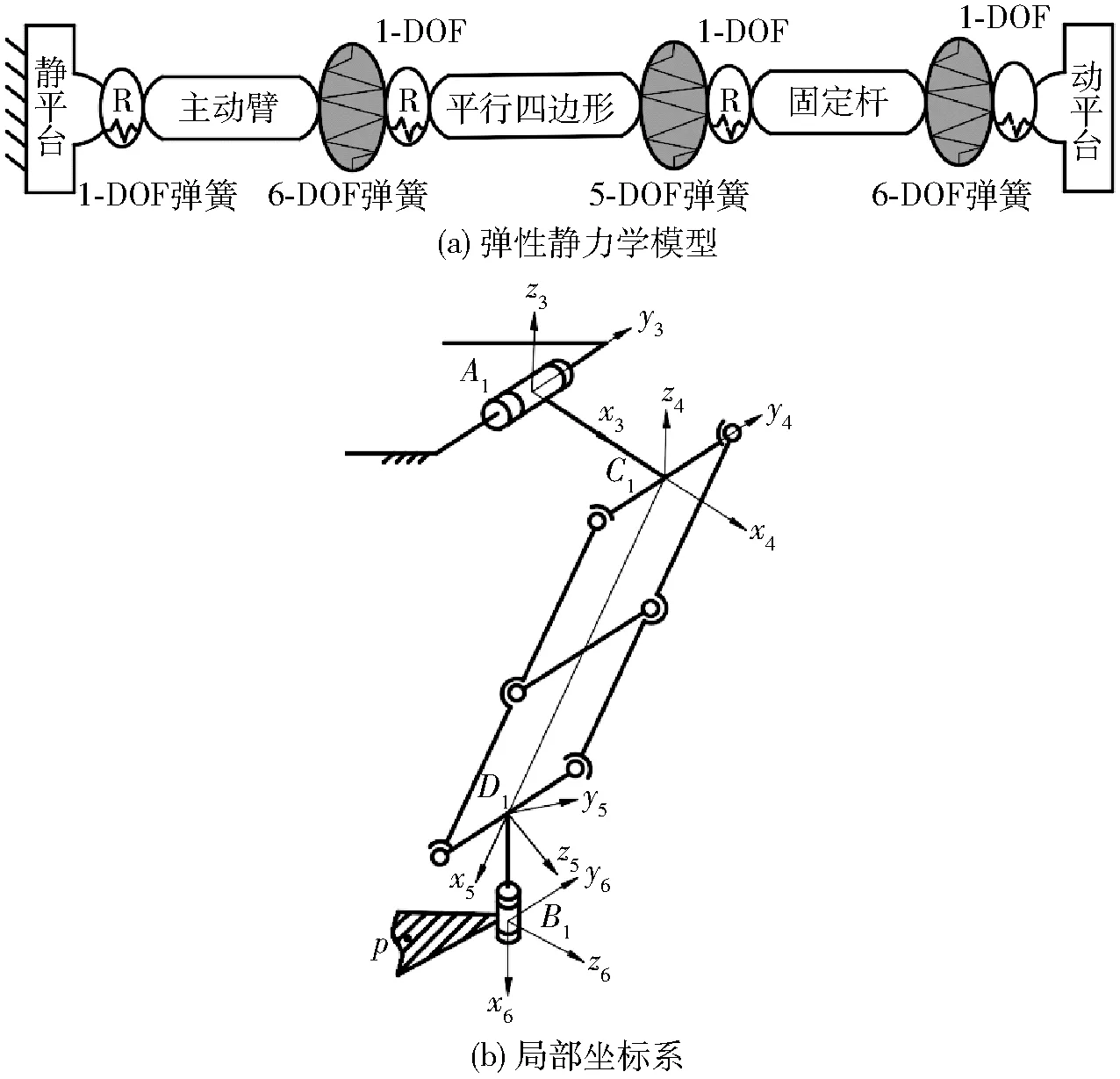
图7 R-(SRS)2-R支链刚度建模Fig.7 Stiffness modeling of R-(SRS)2-R branch
在第1条支链中建立图7b所示的局部笛卡尔坐标系C1x4y4z4、D1x5y5z5、B1x6y6z6,其中x4轴沿A1C1方向,x5轴沿C1D1方向,x6轴沿D1B1方向,y4轴和y6轴平行于中心为A1的转动副轴线方向,z5轴垂直于x5轴和y5轴形成的平面。
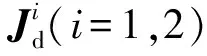
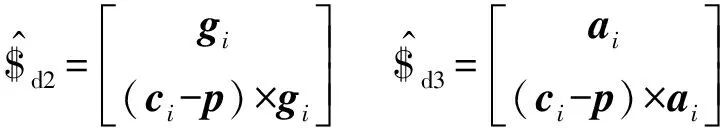
根据式(14)得到Ki(i=1,2),由式(15)得到机构整体的刚度矩阵K。
2.2 刚度性能指标
将笛卡尔刚度K矩阵拆分为量纲一致的子矩阵
(16)
式中Kmr、Kmt、Kfr、Kft——量纲一致的3×3子矩阵
用无量纲化参数的方法[16]对刚度矩阵式(16)进行分析,将外力f和力矩m分开表示[17],即
(17)
其中
式中 Δγ——转动变形量 Δε——移动变形量
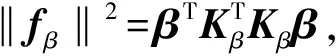
β=Λβpβ
(18)
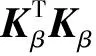
pβ——与向量β等维的系数向量
在不同矩阵下,用无量纲参数将Δγ、Δε表示为
(19)
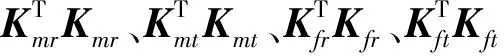
λγ、λε、ωγ、ωε——对应的无量纲向量
将式(19)代入式(17)得
(20)
其中Gm=[KmrΛγKmtΛε]λ=[λγλε]
Gf=[KfrΩγKftΩε]ω=[ωγωε]
式中Gm、Gf——m、f的量纲一致的系数矩阵
用系数矩阵Gm和Gf的欧几里得范数定义机构在不同位姿下刚度的性能指标κm(N·m)和κf(N),即
(21)
由欧几里得范数的性质可知,指标越大,则机构的刚度性能越好。
2.3 数值算例和分析
机构相关参数如表1所示。

表1 机构参数Tab.1 Mechanism parameters
为了分析3T1R机构在不同位姿下的刚度性能,分别对动平台在z方向的不同高度和不同转角φ进行分析。
根据机构运动逆解方程(10),从机构的可达工作空间中取底面半径为100 mm,高为90 mm的圆柱体的工作空间,如图8所示。设定动平台转角φ=0°,通过对机构在工作空间中圆柱顶部(z=-100 mm)和底部(z=-230 mm)进行刚度分析。
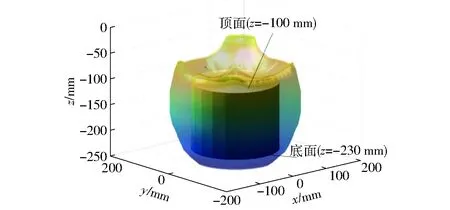
图8 工作空间Fig.8 Workspace
计算κm、κf指标值如图9、10所示。由图9可知,动平台在定姿态φ=0°时,机构的刚度性能指标值图谱在静坐标系关于y=x对称,这一点符合机构结构的部分对称特征。机构刚度指标的峰值都出现在对称轴两侧,并且在顶部和底部不同高度上,峰值分布差异较大。另外R-(SRS)2-R支链的刚度明显大于R-S-S支链,这是由于平行四边形回路具有较大的刚度特性。
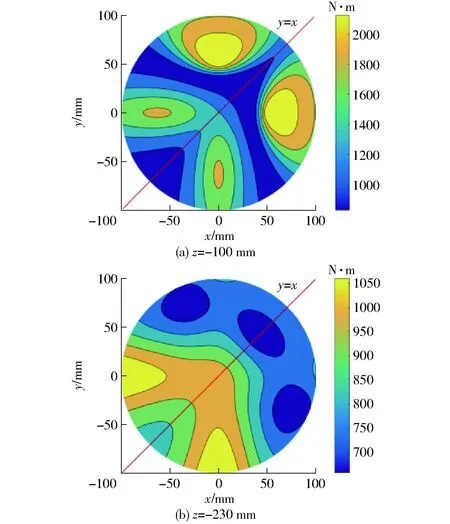
图9 不同高度下的κm等高线Fig.9 Contours at different heights when φ=0°
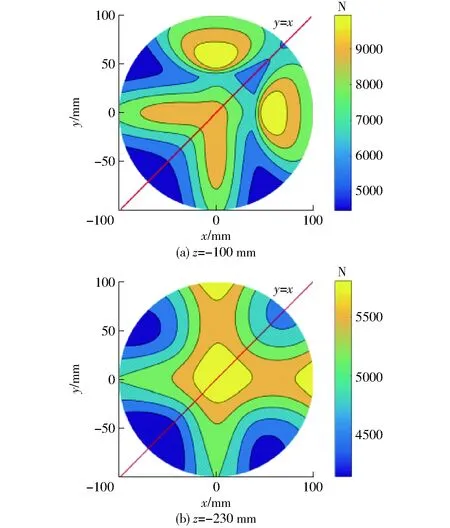
图10 不同高度下的κf等高线Fig.10 Contours at different heights at φ=0°
对比图9a、9b可以发现,在抵抗扭转变形的能力上,工作空间顶部均优于底部,顶部峰值靠近复杂支链R-(SRS)2-R一侧,而在工作空间底部,刚度峰值接近简单支链RSS;在抵抗力变形的能力上,如图10所示,顶部图10a和底部图10b的刚度性能仍存在明显差异,越接近高度顶部时,机构的抗变形能力越优,当在顶部时,抵抗扭转变形和抵抗力矩变形的性能分布相似。
当动平台转角φ=±45°时,机构底部在工作空间中刚度性能的变化如图11所示。可见,当转角φ=±45°时,两种姿态下机构的刚度性能分布也沿y=x轴线对称。图形四周的刚度特性变化较大,中心易出现极值。比较指标κm和κf的变化趋势,可以发现在底部时,机构扭转刚度和线刚度的变化趋势相似。
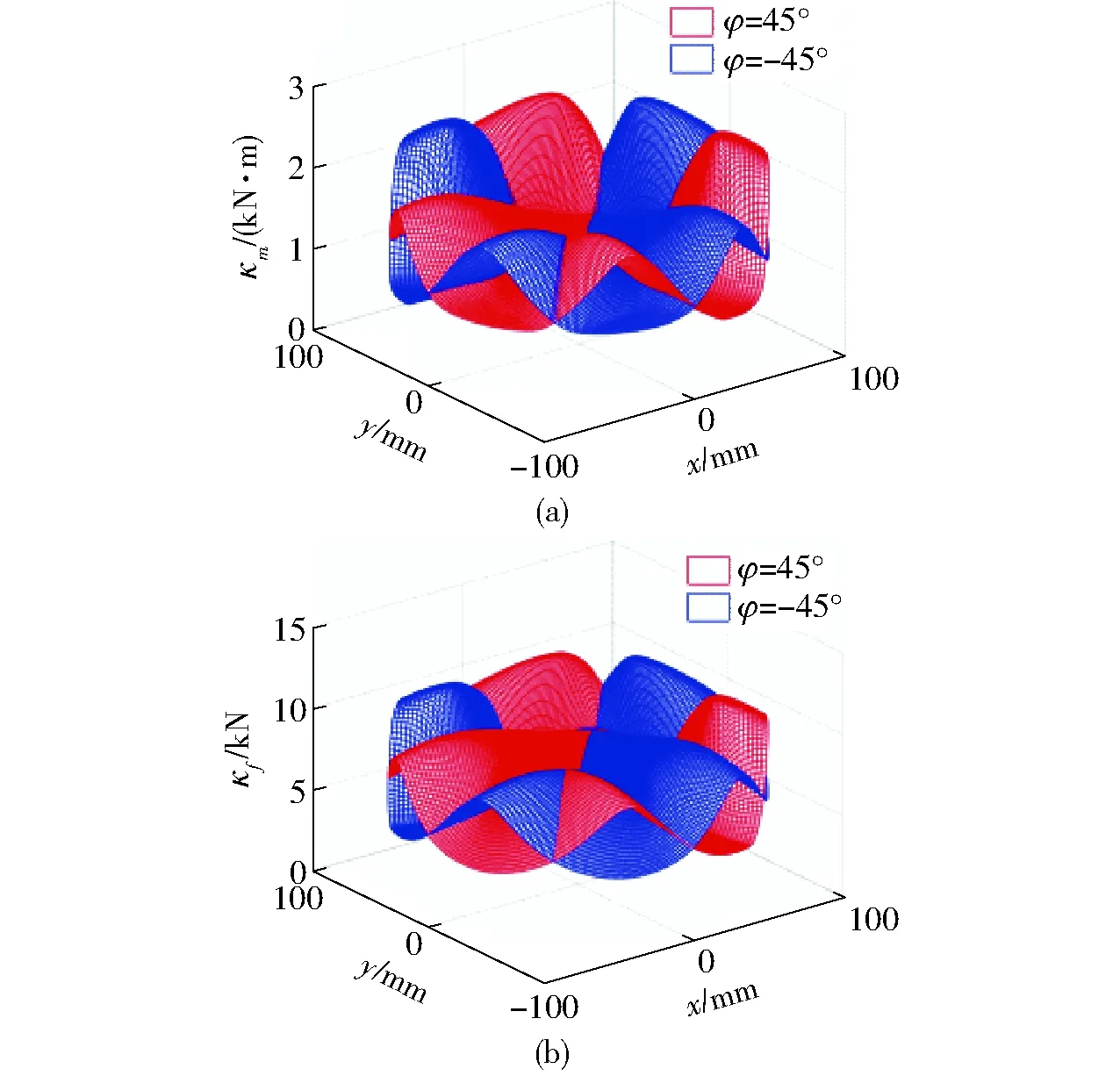
图11 φ=±45°时刚度指标等高线Fig.11 Stiffness index contour line at φ=±45°
3 动力学分析
3.1 动平台速度、加速度分析
(22)
(23)
对式(5)、(6)两边同时对时间求导,得
(24)
(25)
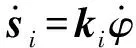
ki=r(-s(φ+αi),c(φ+αi),0)Τ
式(24)、(25)两边分别点乘vi、wi,可得
(26)
(27)
由式(26)和式(27)得到机构速度方程为
(28)
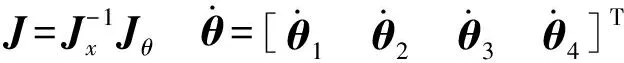
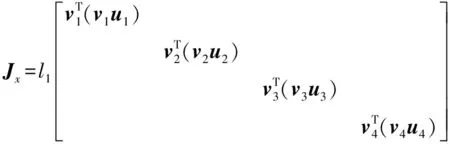
式中J——机构雅可比矩阵
对式(28)求一阶导,整理可得机构加速度方程为
(29)
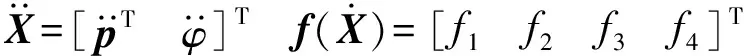
(30)
式中E3——3阶单位矩阵
C——四阶方阵,且矩阵元素C44=1,其余都为0
3.2 支链及质心点速度、角速度分析
设机构第i支链上Ai点的坐标系为{Ai},Ci点的坐标系为{Ci},Di点的坐标系为{Di};Bi点的坐标系为{Bi},如图5和图7所示。上述各坐标系{O}到{Ai}的旋转变换矩阵记为AiRO,以此类推。
在{Ai}坐标系下,主动臂AiCi质心速度为
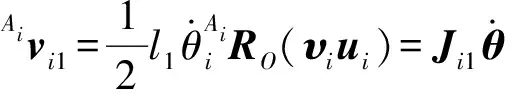
(31)
其中
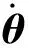
则质心Ci速度为
Aivci=2Aivi1
(32)
在{Ai}坐标系下,因为短杆DiBi(i=3,4)与动平台保持垂直,且动平台绕着其法线方向转动,因此点Di、Bi的速度和DiBi杆的质心点速度相等,即
Aivbi=Aivdi=Aivi3(i=1,2)
(33)
由式(31)和式(33)可得从动臂CiDi质心点速度为
(34)
其中
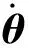
在坐标系{Ai}下,点Bi的速度为
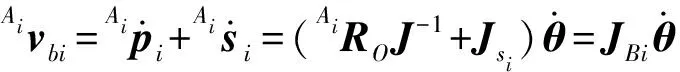
(35)
其中
JBi=AiROJ-1+Jsi
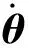
由式(31)和式(33)得从动臂CiBi质心点速度为
(36)
其中
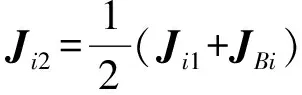
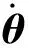
对式(26)两边同时叉乘Aivi,可得从动臂CiDi(i=1,2)在坐标系{Ai}的角速度为
(37)
式中Ui——ui2的反对称矩阵
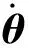
对式(27)两边同时叉乘Aivi,可得从动臂CiBi(i=3,4)在{Ai}坐标系的角速度为
(38)
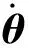
3.3 支链质心加速度、角加速度分析
在坐标系{Ai}下,对式(24)两边关于时间求一阶导,并两边同时叉乘Aivi,化简得从动臂CiDi(i=1,2)的角加速度为
(39)
在坐标系{Ai}下,对式(25)两边关于时间求一阶导,并两边同时叉乘Aivi,化简得从动臂CiBi(i=3,4)的角加速度为
(40)
对式(34)和式(36)求一阶导,可得从动臂CiDi(i=1,2)和CiBi(i=3,4)质心加速度为
(41)
3.4 动力学方程
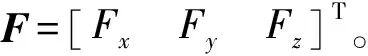
3.5 动力学模型
(1)动平台受力分析
忽略和动平台固连的DiBi杆,不考虑摩擦力的影响,根据达朗贝尔原理可得动平台质心处的惯性力为
(42)
(2)主动臂、从动臂受力分析
在坐标系{Ai}下,主动臂惯性力和惯性力矩可表示为
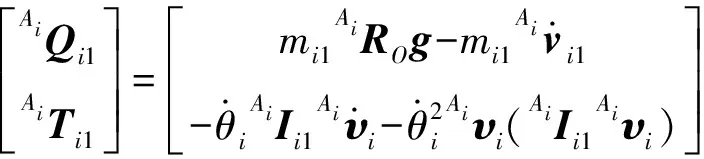
(43)
同理,从动臂惯性力和惯性力矩可表示为
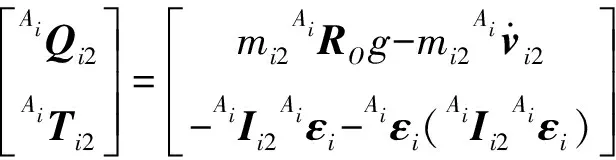
(44)
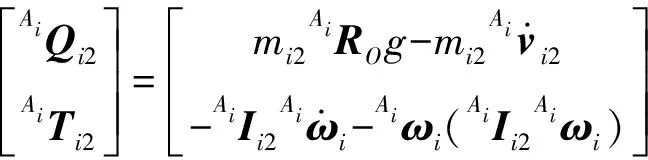
(45)
式中AiQi1、AiQi2——主动臂和从动臂在坐标系{Ai}下的惯性力
AiTi1、AiTi2——主动臂和从动臂在坐标系{Ai}下的惯性力矩
在不同坐标系下,惯性张量矩阵的变换是矩阵的二次型变换[18],即
式中AiIi1——主动臂AiCi在坐标系{Ai}下的惯性张量矩阵
Ii1——主动臂AiCi在坐标系{Ci}下的惯性张量矩阵
AiIi2——从动臂CiDi和CiBi在坐标系{Ai}下的惯性张量矩阵
Ii2——从动臂CiDi和CiBi在{Di}(i=1,2)、{Bi}(i=3,4)坐标系下的惯性张量矩阵
(3)动力学模型
根据虚功原理[19-20],机构动力学方程为
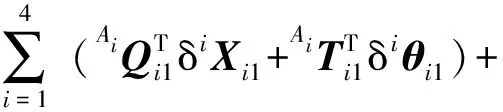
(46)
其中
式中M——驱动力矩矢量
δX、δθ——动平台质心处的虚位移和虚转角位移矢量
δiXi1、δiXi2——驱动臂、从动臂在坐标系{Ai}下的虚位移矢量
δiθi1、δiθi2——驱动臂、从动臂在坐标系{Ai}下的虚转角位移矢量
(47)
将式(47)代入式(46),整理得
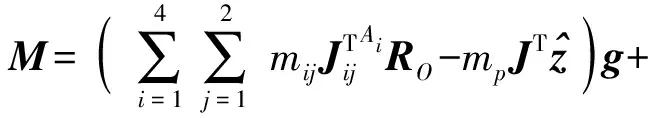
(48)
3.6 算例仿真
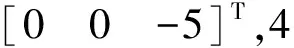
(49)
根据动力学模型式(48)可计算出4条主动臂的输入转矩,将计算所得的驱动力和ADAMS模型仿真所得的进行比较,如图12所示。由图12可得,两者结果相差不大,表明动力学方程式(48)的正确性。仿真误差主要是由于ADAMS模型中没有考虑机构重力的影响造成的,且惯性参数设置误差和质量参数的估算误差也是原因之一。
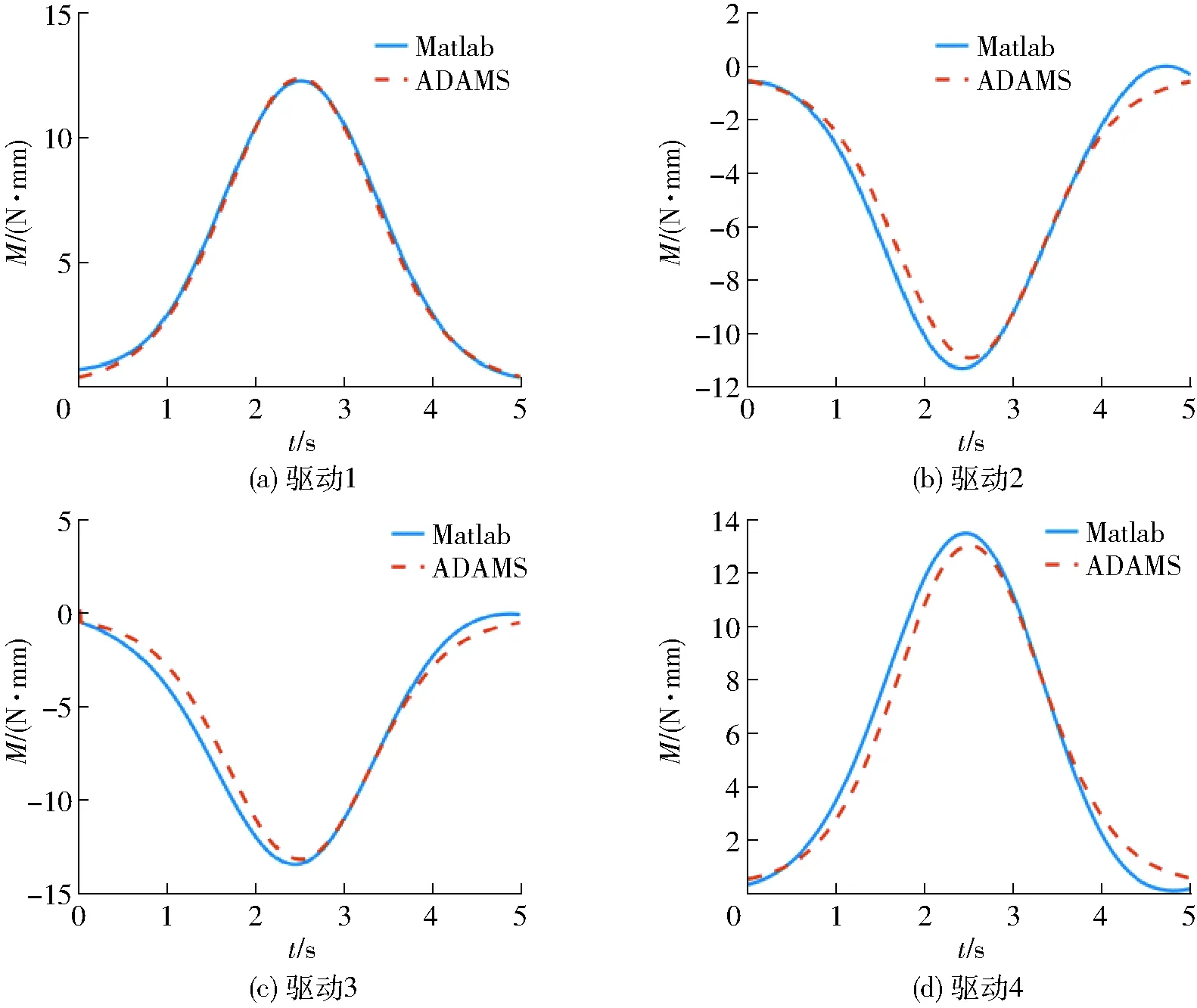
图12 仿真结果对比Fig.12 Comparison of simulation results
4 结论
(1)运用虚拟弹簧法对3T1R机构进行了刚度建模,得到了机构笛卡尔空间的刚度矩阵。针对机构的转动和移动刚度性能指标,分别分析了机构在不同工作平面的刚度特性,结果表明,动平台越往上,工作高度越高,刚度性能越好,且刚度性能指标值分布关于y=x轴对称,符合机构结构特点。
(2)推导了机构动平台和各支链的速度、加速度和受力方程;基于虚功原理建立了机构的动力学方程,并通过ADAMS模型仿真结果进行了对比,验证了动力学模型的正确性。

