泵站进水池吸入口涡旋结构及湍流特性的大涡模拟

张德胜 李普熙 赵睿杰 潘 强 施卫东

(1.江苏大学流体机械工程技术研究中心， 镇江 212013； 2.南通大学机械学院， 南通 226019)

0 引言

泵站进水池是供安装有水泵的吸水管直接取水的水工建筑物，一般布置在前池与泵房之间或在泵房之下。进水池或引水渠方位设置不当引起的不均匀行进水流、流速梯度较大的剪切流、沿行进水流方向设置几何体或障碍物引起的旋转尾流等都会诱发涡旋[1-2]。水泵进水池可能形成的涡旋主要分为自由表面涡和液下涡两类：前者是由于喇叭口吸力拉拽自由表面的圆柱绕流产生的涡旋而形成的吸气涡，后者主要是由于喇叭口吸力和水流受壁面形状约束形成的局部涡流而产生的吸入涡。而这些高度不稳定的涡旋会影响进水池水流的流态，不均匀流态被水泵吸入后，将影响水泵运行效率，甚至导致水泵发生空化现象，产生振动和噪声，严重时会导致整个机组不能正常工作。

进水池中的水流运动具有强烈的三维各向异性湍流特性，由于泵站进水池原型尺寸较大，为研究进水池内部流场，常按一定比例缩放进行模型实验。文献[3]在对水泵进水口涡旋方面的实验研究中，通过采用传统的染色法显示涡旋的发生，并应用PIV(Particle image velocimetry)测量技术捕获涡旋的数目、位置、形状、大小及强度等定量信息。文献[4-5]对进水池中自由表面涡和液下涡进行数值模拟，湍流模型采用的是标准k-ε双方程模型，计算结果可显示涡旋的大小和位置，其涡量的大小反映涡旋的强度，但对比PIV实验发现，数值模拟计算出的涡旋偏大，强度偏弱。文献[6-7]对比了不同湍流模型在泵站进水池涡旋模拟中的适用性。文献[8]通过PIV实验研究自由表面涡的形成和演化，并通过数值模拟预测涡旋的位置及结构。文献[9-10]为更好地了解大涡模拟(LES)对进水池流态的预测性能，将剪切应力传输(SST)模型的模拟结果与LES的模拟结果进行比较，LES可以更准确地模拟主流和湍流统计量。文献[11]用LES对小型水力发电站进水池中具有大涡流的局部区域三维非定常流动进行数值模拟，并用λ2(速度梯度的第二不变量)准则将水电站进水池中的涡三维可视化。文献[12]为研究轴流泵装置进水涡旋从生成到溃灭的过程对压力脉动的影响，用数值模拟及高速摄影实验对比此过程，揭示喇叭管下方激励源为涡旋的压力脉动与叶轮进口断面处压力脉动的关系。文献[13]用VOF(Volume of fluid)方法结合LES对进水池流动进行模拟，并与ADV(Acoustic Doppler velocimetry)实验结果进行对比。

涡旋结构与周围流场的湍流特性很难通过实验获得，而数值模拟可以提供流场局部细节信息。研究表明，基于RANS湍流模型的数值模拟可以提供相对准确的时均流场特性，而LES方法可以捕获进水池中更加精细的流动特征。此外，对LES模型的验证还缺乏系统的分析，对进水池涡流的产生和发展机理也缺乏深入的了解。本文利用LES模型和VOF方法相结合的方法进行数值模拟，并与实验结果进行比较，讨论两者之间异同。在此基础上，揭示涡旋周围各向异性湍流结构，研究涡旋核心向周围湍流的动量传递过程。

1 数值方法

1.1 几何模型

以PIV实验的泵站进水池作为研究对象，图1为进水池三维示意图。内径d为0.075 m的吸水管和直径D为0.115 m的喇叭口垂直安装在矩形进水池中，进水池长为1.22 m，宽为0.3 m(4d)。喇叭口到底部的距离为0.9d，吸水管轴线距后壁0.9d，吸水管从进水池中吸水，流量恒定为0.004 m3/s，吸水管中的平均流速Up=0.9 m/s，进水流道平均速度Um=0.12 m/s。吸水管内雷诺数Rep大约为75 000。根据实验数据,基于吸水管直径和速度的Froude数和Weber数分别约为1.1和840。

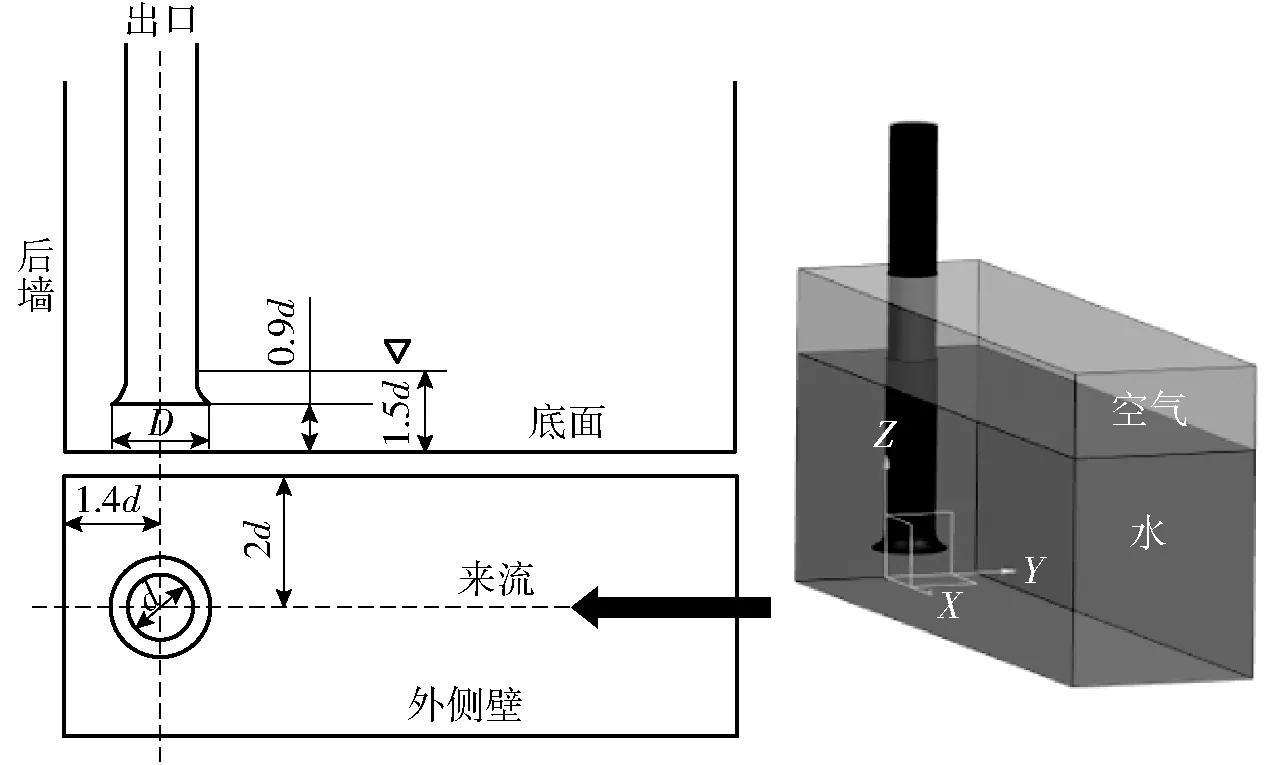
图1 进水池三维示意图Fig.1 Schematic of pump sump

1.2 控制方程

用六面体结构网格生成计算域，在商用CFD软件ANSYS CFX 14.5中求解质量和动量守恒方程。流体假定是不可压缩和等温的。大涡模拟的基本思想是可解尺度(大尺度脉动)湍流由方程直接数值求解，不可解尺度(小尺度脉动)湍流的质量、动量和能量运输对大尺度运动的作用采用建立模型(亚格子模型)的方法模拟，从而使可解尺度运动方程封闭。在LES中，过滤尺度Δ通常与局部单元尺寸相同，对小于该方程尺寸的涡流进行方程封闭建模，过滤后的控制方程表示为

(1)

(2)

t——时间，s

ρ——水密度，kg/m3

v——运动粘度，m2/s

gi——重力加速度，m/s2

xi、xj——i、j方向位移

τij——亚格子尺度应力，m2/s2

对于亚格子尺度(SGS)应力，涡流粘度模型的定义为

(3)

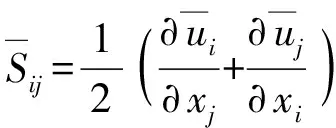
(4)

(5)

(6)

Δ=(ΔxΔyΔz)1/3

(7)

式中τkk——亚格子尺度应力τij中角标相同的应力分量，m2/s2

δij——克罗内克函数

vsgs——亚格子湍流粘度，m2/s

Δx、Δy、Δz——网格在3个方向间距的平均值

Cw——自由衰减的各向同性均匀湍流校准常数，取0.5

xk——k方向位移

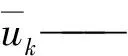
本文采用壁面适应局部涡粘模型(WALE)求解亚格子应力，该模型可以检测到与动能耗散相关的所有湍流结构且可以通过线性不稳定增长模式来再现层流到湍流的过渡过程[14]。

1.3 自由表面处理

本文中，液面波动较小，主要研究对象在液面以下，且对自由液面处的网格沿Z轴加密处理，使得VOF方法对界面的捕捉更精确。VOF模型是建立在固定的欧拉网格下的表面追踪办法，建立在两种或者多种流体(或相)不互相混合的前提下。当需要得到一种或多种互不相融的流体交界面时，可以采用VOF模型。在此模型中，不同流体组分共用着一套动量方程，通过引进相体积分数这一变量，实现对每一个计算单元相界面的追踪。在每个控制容积内，所有相体积分数总和为1。在单元中，若第n相流体体积分数为αn，当αn=0，单元内不存在第n相流体；当αn=1，单元内充满了第n相流体；当0<αn<1，单元里包含了第n相流体和一相或其他多相流体的界面。跟踪相之间的界面通过求解容积比率的连续方程来完成。对第n相，有

(8)

(9)

式中V——速度

1.4 边界条件及设置

泵站进水池中的流态受进口边界条件影响很大。进口速度与PIV实验测量的进口截面时均速度相同，模型中进口距离吸水管较远，水流通过进水池可以得到充分发展。为恒定水位，在出口处指定等于入口的质量流量边界。在CFX中定义在整个计算域中的初始水位和水中初始静压。壁面设置光滑无滑移。顶部设置为开口，使空气可流入或流出边界。RNGk-ε湍流模型可以很好地处理带旋流、高应变率流动及流线弯曲程度较大的流动[15]。为了节约计算时间，首先在约3 800次迭代、速度分量的残差从初始值降低4～5个数量级后，获得基于RNGk-ε湍流模型的结果。在CFX 14.5中RNGk-ε湍流模型默认的壁面函数为可缩比例壁面函数(Scalable wall functions)，该壁面函数对于任意细化的网格，能给出一致的解。然后，以该定常结果作为非定常大涡模拟的初始条件。瞬态控制方程的离散采用有限容积法，瞬态项采用二阶迎风后插方法，对流项采用中心差分方式。计算时间共50 s，前30 s的时间步长为0.01 s，后20 s的时间步长为0.002 s。两部分计算的库朗数均方根分别约为0.8和0.15，说明这两个时间步长均适用于瞬态模拟。

1.5 网格分辨率和收敛性验证

实验中产生的涡旋近似椎体，涡旋中心区域尺度较小，需要比较精细的网格来捕捉涡旋的特征物理量，在会产生涡旋的区域和近壁区对网格进行加密，共划分3套六面体结构网格，网格数分别为5.0×106、6.8×106和9.5×106，依次在边界及自由液面处加密，本文采用网格数为6.8×106的模型。所有固体边界和自由表面处的第1层网格为1 mm，以满足墙壁处y+为1～3(y+表示第1层网格大小的无量纲量)的要求。网格尺寸从墙壁开始增加，增长率为1.1，以便平滑增加。特别是在涡旋发生的区域中，网格的纵横比需接近于一致，由于网格比较精细，故在靠近墙壁处可以达到4。而精细的网格则需要大量的计算资源，粗糙的网格无法求出足够的涡流，故有必要对网格收敛性进行验证。LES模型和数值误差对精度的影响相反，相互抵消，导致总误差较低[16-18]。为了估算计算的数值精度，采用了文献[19]推荐的既定方法。这种方法是基于Richardson外推理论[20]，并已发展成适用于实际CFD案例的通用公式。经过计算，本文网格解的数值不确定度估计为2.3%。

2 PIV实验验证

将模拟结果与PIV实验作比较，包括自由表面涡、底涡和侧壁涡的位置、形状、大小及涡核强度等方面。实验中每种涡旋均以0.21 s时间间隔拍摄85幅PIV图像做时均处理。LES模拟中的时间步长为0.002 s，求解涡旋的瞬时结果。为避免在初期出现任何不确定性，遂将后17 s的模拟结果进行时均处理。选择底部、侧壁和自由表面上3种典型涡旋的流线和时均涡量场来验证模拟，分别取距离底部和自由表面20 mm截面和距外侧壁60 mm截面来对比。总体来说，模拟与实验具有良好一致性。当比较涡量场时，模拟结果与实验结果一致，如在底涡周围会存在一个二次涡，表面涡为两个旋向相反的涡。通过表1和图2(ωz表示Z方向的涡量)比较底涡和表面涡涡量发现模拟涡量要略小于实验值，模拟中涡量更加集中，涡核极值区域较小，涡形状较实验略小，并且模拟中的涡旋位置与实验中的涡旋位置略有不同，这可能归因于几个因素。首先，LES模型在极小涡核半径区域模拟计算会产生偏差，如果局部网格尺寸不够小，可能会对不准确的值进行建模。另外，边界条件也存在不确定性，例如入口处速度为PIV拍摄时均速度而实际中入口处流速是不断变化的，且缺乏入口湍流强度数据。因此，不可能在数值和实验之间获得完美匹配。但LES显示出比其他基于RANS(雷诺时均)的模拟更好的预测能力，如涡旋的位置、形状、大小以及涡核内的涡量和湍动能的分布[9-10]。总体来说，本文LES与VOF方法模拟结果与实验结果基本一致，模拟结果可用于深入分析。

表1 涡心涡量(ωzd/Up)Tab.1 Vorticity of vortex center

图2 模拟与实验结果对比Fig.2 Comparison of LES and experiment for three kinds of vortices

3 结果与讨论

3.1 表面涡和底涡与湍流的相互作用

基于LES精确求解的涡流速度场，可以分析湍动能、雷诺应力等湍流信息，揭示涡旋和湍流之间的相互作用，这在实验或基于RANS的模拟中很难实现。由于附壁涡强度较弱且难以识别，不利于分析，本文只选择底涡和自由表面涡作为研究对象，揭示涡旋与周围流场的作用机理。模拟中的涡旋切向速度计算公式为

(10)

式中R——以涡心为圆心的任意半径，m

Γ——在半径为R的圆内的速度环量，m2/s

定义压力最低点为涡心，得到切向速度Vθ在半径方向的分布，将Vθ峰值对应的半径定义为涡核半径，即涡旋特征半径。

通过λ2等值面将涡旋可视化，如图3所示，λ2定义为

(11)

图3a中λ2阈值设为300 s-2，A为自由液面，B为自由表面涡，C为环绕在自由表面涡附近的二次涡。随着主涡向喇叭口延伸，二次涡螺旋环绕在自由表面涡周围并与自由表面涡相互作用。图3b中λ2阈值设为600 s-2，可以看到底涡和环绕底涡的二次涡。λ2阈值的设定是为了使模拟中可视化的涡旋形状与实验中所能观察到的涡旋一致。

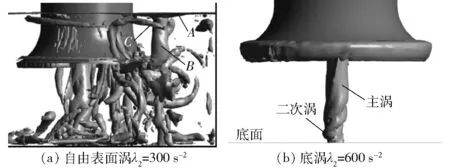
图3 λ2等值面Fig.3 Iso-surfaces of λ2

图4(T1～T3表示3个连续时刻)为距离自由液面和底面10 mm处，表面涡和底涡在3个连续时刻的切向速度分布，展示了涡旋的减弱过程。将直角坐标系下的雷诺应力转化为圆柱坐标，揭示涡核区域与相邻区域的湍流特征，公式为

(12)

其中

ur=uxcosθ+uysinθ

(13)

uθ=-uxsinθ+uycosθ

(14)

式中ux、uy——x、y方向速度分量，m/s

ur——圆柱坐标中径向速度分量，m/s

uθ——圆柱坐标中切向速度分量，m/s

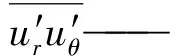
θ——圆柱坐标系中的极角

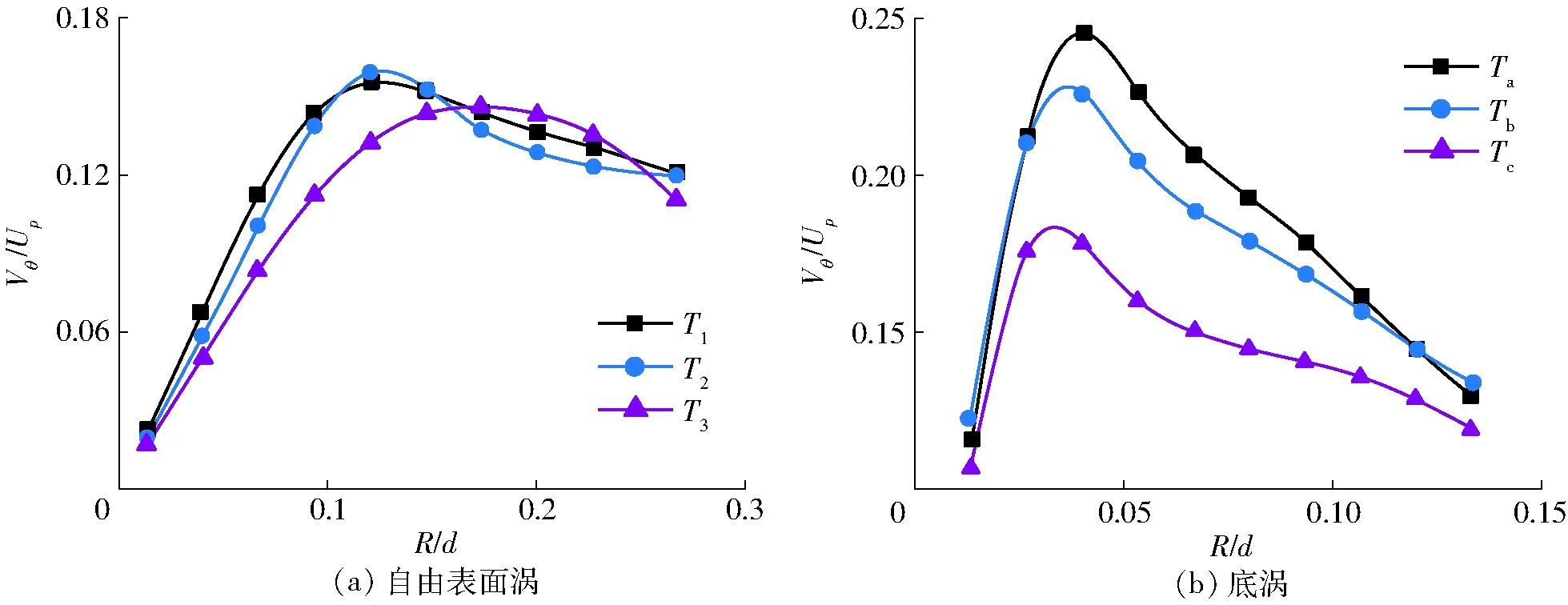
图4 切向速度分布Fig.4 Distribution of Vθ

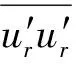
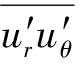
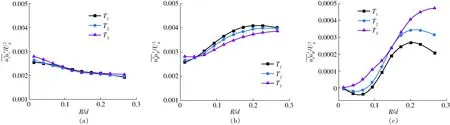
图5 随时间变化的自由表面涡雷诺应力Fig.5 Temporal change of Reynolds stresses for free-surface vortex

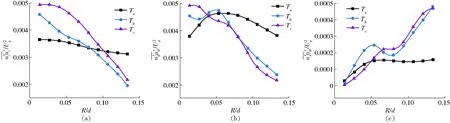
图6 随时间变化的底涡雷诺应力Fig.6 Temporally changes of Reynolds stresses for floor-attached vortex

3.2 自由表面涡和底涡的空间特性

为研究涡旋的空间特性，创建距自由表面10、20、30 mm的3个平面(Z1～Z3)和距底面50、40、30、20、10 mm的5个平面(Z4～Z8)，如图7所示。

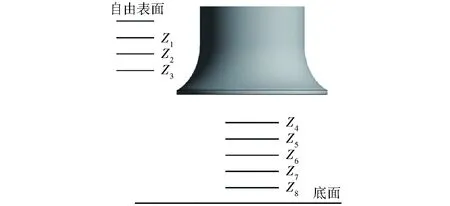
图7 截面示意图Fig.7 Schematic of positions of different planes

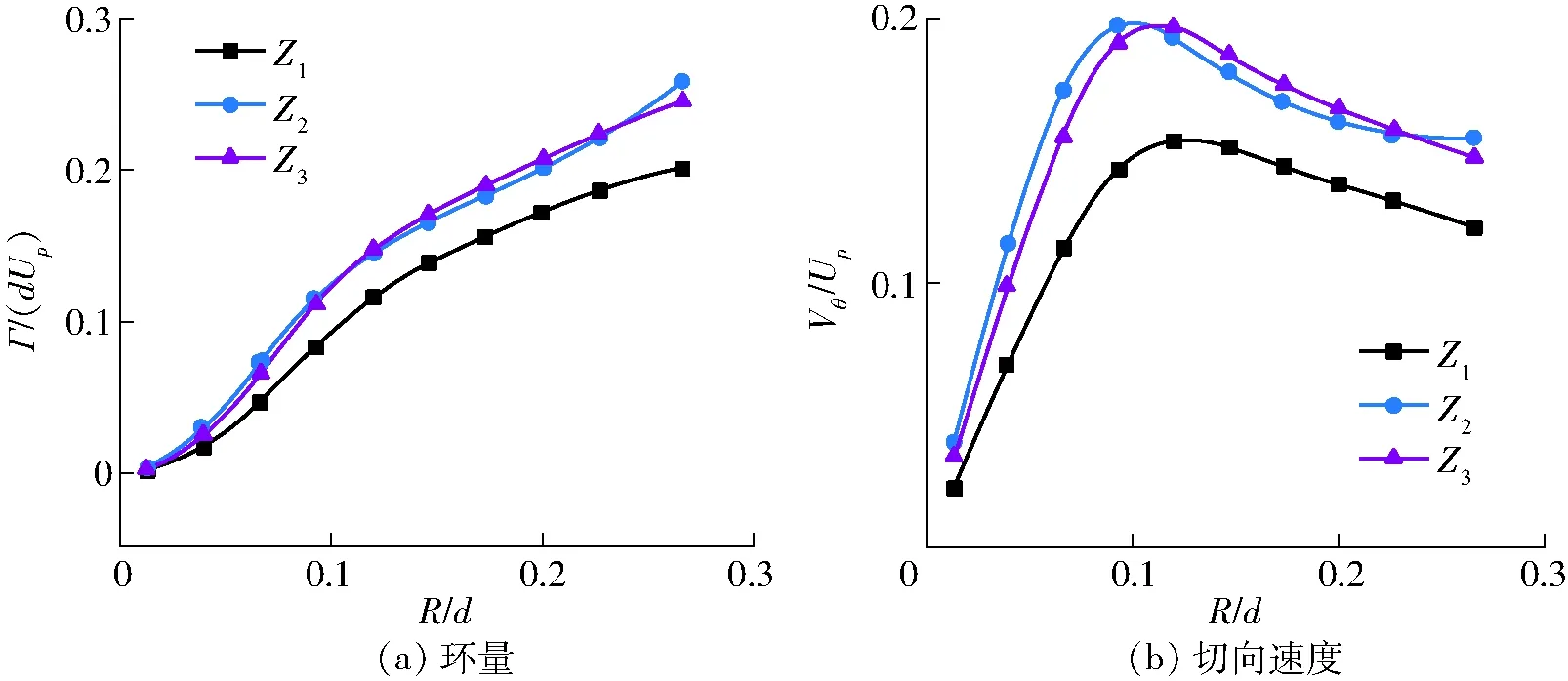
图8 自由表面涡Vθ和Γ的空间分布Fig.8 Spatial distributions of Vθ and Γ for free surface vortex

图8a和图9a为自由表面涡和底涡在不同截面处的环量分布，随着涡旋向喇叭口靠近，环量逐渐汇聚增大。图8b中，自由表面涡在Z2和Z3平面的涡核半径稍小于Z1，在Z2和Z3平面涡旋更加集中，涡旋呈现出锥形。底面涡涡核半径从底面开始先增大后减小，底面涡涡核呈现梭型，这可能是由于无滑移边界阻碍了流动的圆周运动。

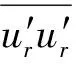
图9 底涡Vθ 和Γ的空间分布Fig.9 Spatial distributions of Vθ and Γ for floor-attached vortex

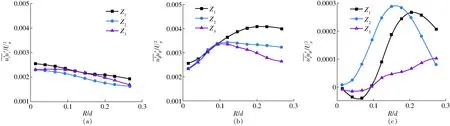
图10 自由表面涡雷诺应力的空间分布Fig.10 Spatial distributions of Reynolds stressses for free surface vortex

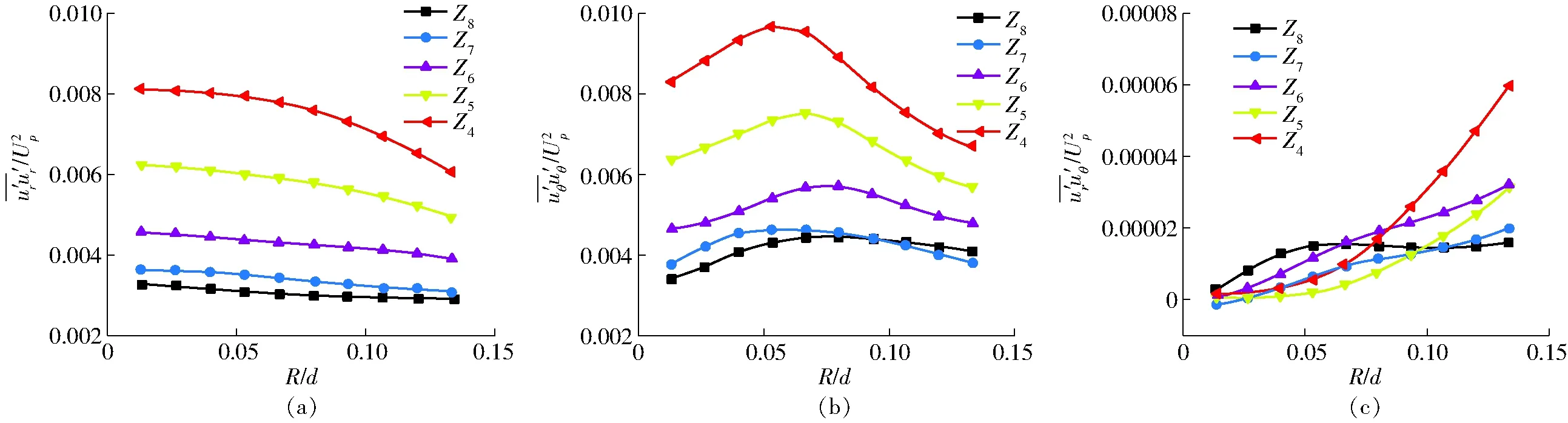
图11 底涡雷诺应力的空间分布Fig.11 Spatial distributions of Reynolds stressses for floor-attached vortex

4 结论

(1)将LES及VOF方法的数值模拟结果与PIV实验进行对比，结果相差不大，表明模拟结果可以用来进一步分析二阶湍流参数，如湍动能和雷诺应力等。

(2)结合LES及VOF方法模拟泵站进水池内的旋涡流动，经过计算，网格解的数值不确定度估计为2.3%。根据实验对模拟结果进行定性和定量验证，在涡旋的位置、大小、方向和形状方面有良好的一致性。