基于流变特性分析的菠菜有序收获机夹持输送装置研究
邹亮亮 刘雪美 李金光 牛子孺 宋烨本 苑 进
(1.山东农业大学机械与电子工程学院, 泰安 271018; 2.山东省园艺机械与装备重点实验室, 泰安 271018)
0 引言
目前菠菜收获机械多采用无序采收的形式,这种采收机械虽然结构简单,但是由于割茬收获易腐烂、损伤严重、不易长期储存,而且无序收获不便于菠菜的打捆收集[1-2]。针对无序收获存在的问题,研制了一种采用根土铲切、夹持输送形式的菠菜整株有序收获机械。但是,菠菜在机械收获过程中,植株极易受到夹持输送装置的挤压而产生机械损伤。
为了探究果蔬受到挤压作用的损伤机理,常采用有限元分析的方法对果蔬进行建模,通过分析果蔬受到挤压作用时的表皮和内部组织应力分布,揭示其损伤机理[3-6]。但是,进行有限元分析通常需要设定果蔬为弹性体,不能很好地表示出本身的粘弹性特性[7],而且菠菜相对其他果蔬形状不规则,不易于有限元建模,因此研究菠菜的流变特性对揭示菠菜损伤机理具有重要的意义。
国内外学者对某些果蔬的流变特性已做了相关研究[8-15],但是对绿叶菜的流变特性鲜有报道。本文通过研究菠菜的流变特性,分析夹持输送装置工作参数对菠菜夹持损伤的影响。
1 夹持输送装置结构与力学分析
1.1 结构与工作原理
菠菜有序收获机主要由铲切装置、夹持输送装置和行走装置等组成,如图1所示。铲切装置将菠菜的根部铲断,主要包括根土铲和参数调节装置;夹持输送装置将菠菜夹持拔取,并有序输送;行走装置通过外界牵引力驱动收获机前行。
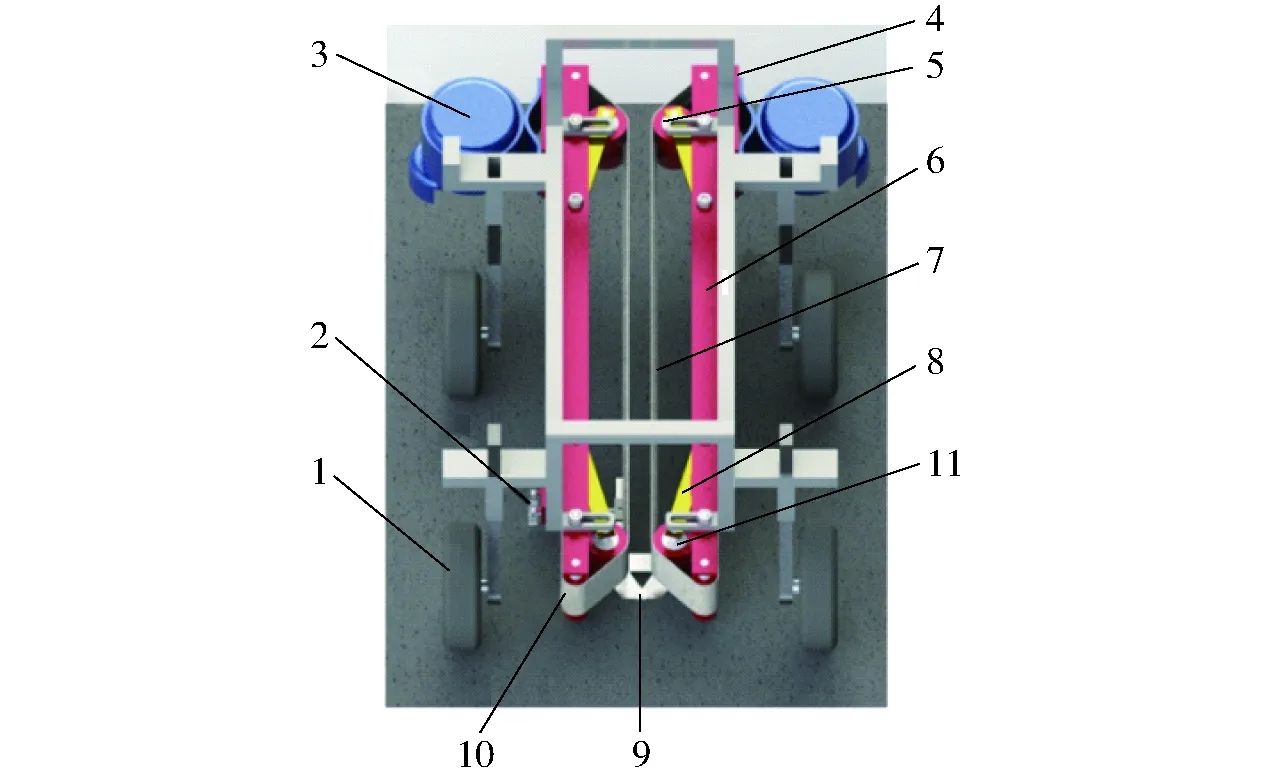
图1 菠菜收获机整机结构图Fig.1 Schematic of spinach harvester1.车轮 2.根土铲参数调节机构 3.调速电机 4.驱动轮 5、11.夹持轮 6.机架 7.夹持带 8.浮动夹持机构 9.根土铲 10.张紧轮
菠菜夹持输送装置是菠菜有序收获机核心部件,为了实现有序收获,采用带式夹持结构,主要由驱动轮、张紧轮、夹持带、浮动夹持机构等部件组成,如图2所示。收获过程中,驱动轮在调速电机的带动下转动,带动两条夹持带同速运动,夹持带带动两组夹持轮转动,当菠菜植株进入到夹持轮间隙时,随着夹持轮的转动,菠菜植株被带离地面,并随着夹持带的定向移动而完成输送过程。
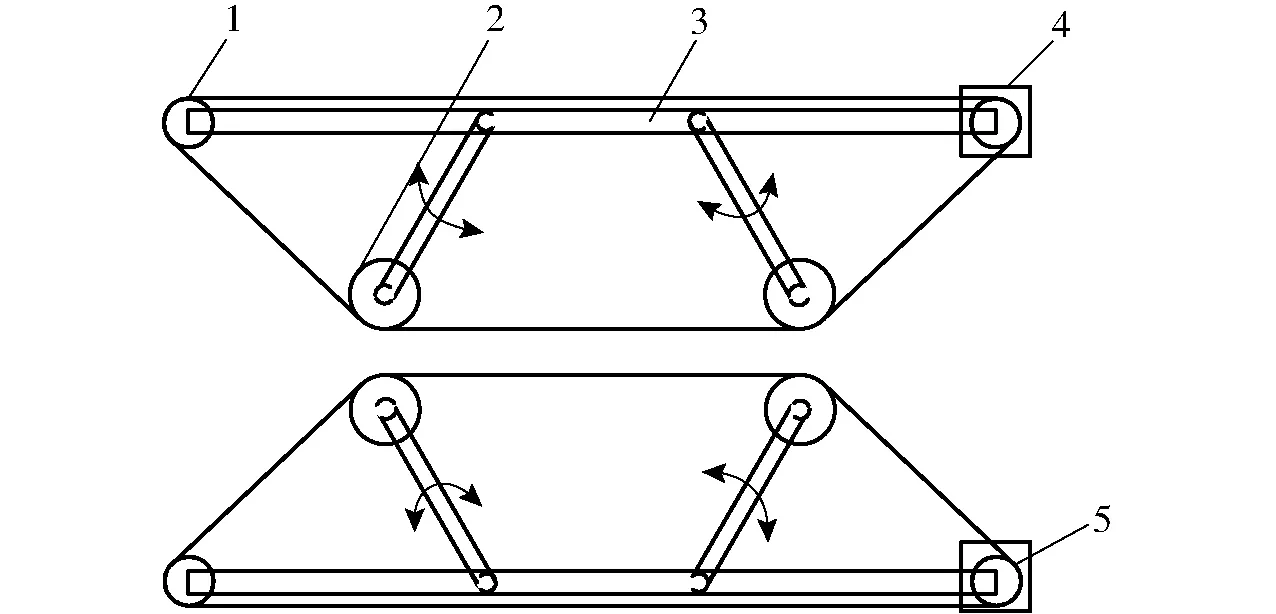
图2 夹持输送装置结构示意图Fig.2 Schematic of clamping conveyer device1.张紧轮 2.浮动夹持机构 3.夹持输送装置机架 4.调速电机 5.驱动轮
菠菜夹持输送过程中植株受到夹持轮以及夹持带的挤压作用极易受到机械损伤。根据菠菜在夹持输送过程挤压变形的不同,分为以下两个过程:菠菜夹持拔取过程,此过程菠菜受到的挤压力随着菠菜的变形而增加,当菠菜完全被夹持轮夹持时,受到的挤压力最大;菠菜输送过程中菠菜在夹持带之间,由于张紧轮的作用使得夹持带间距保持不变,因而此阶段菠菜的挤压变形量保持不变,出现应力松弛现象。
夹持过程中通过张紧轮使夹持带始终处于张紧状态,改变调速电机转速可以调节夹持输送速度,通过浮动夹持机构实现对菠菜的柔性夹持。
1.2 浮动夹持机构设计
1.2.1浮动夹持机构
浮动夹持机构由夹持轮、支撑杆、扭簧、扭簧刚度调节螺栓组成,浮动机构的结构如图3所示。

图3 浮动夹持机构结构示意图Fig.3 Schematic of floating clamping mechanism1.夹持轮 2.支撑杆 3.拔取输送装置机架 4.扭簧 5.扭簧刚度调节螺栓
1.2.2浮动夹持过程运动分析
从菠菜刚被夹持轮挤压到菠菜植株挤压变形至最大这段时间,满足如图4所示的几何关系。
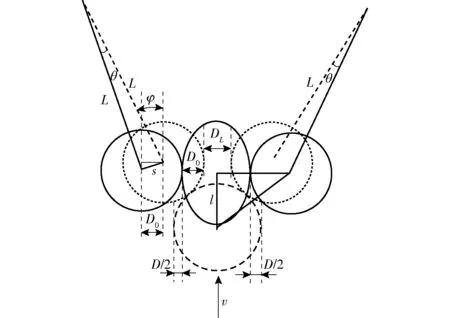
图4 浮动机构运动过程分析Fig.4 Analysis of moving process of floating mechanism
由于收获过程浮动量较小,浮动角θ取值较小,近似存在几何关系
(1)
式中D0——单个夹持轮的浮动量,mm
L——支撑杆长度,为135 mm
φ——支撑杆与机架的夹角,为0.13 rad
菠菜在夹持过程中满足几何关系
D=2R-2D0-DL
(2)
式中D——菠菜的变形量,mm
R——菠菜夹持部位半径,mm
DL——夹持带的初始间距,为10 mm
(3)
式中r——夹持轮半径,mm
l——喂入过程菠菜输送距离,mm
根据式(2)、(3)求得挤压速度与输送速度的关系为
(4)
式中v1——菠菜被挤压的速度,mm/s
v2——喂入过程菠菜输送速度,mm/s
菠菜植株喂入结束后通过夹持带完成输送过程,所用的时间T为
(5)
式中L2——夹持输送带长度,为450 mm
vm——输送速度,mm/s
1.2.3浮动夹持过程力学分析
对浮动夹持过程进行受力分析,如图5所示。
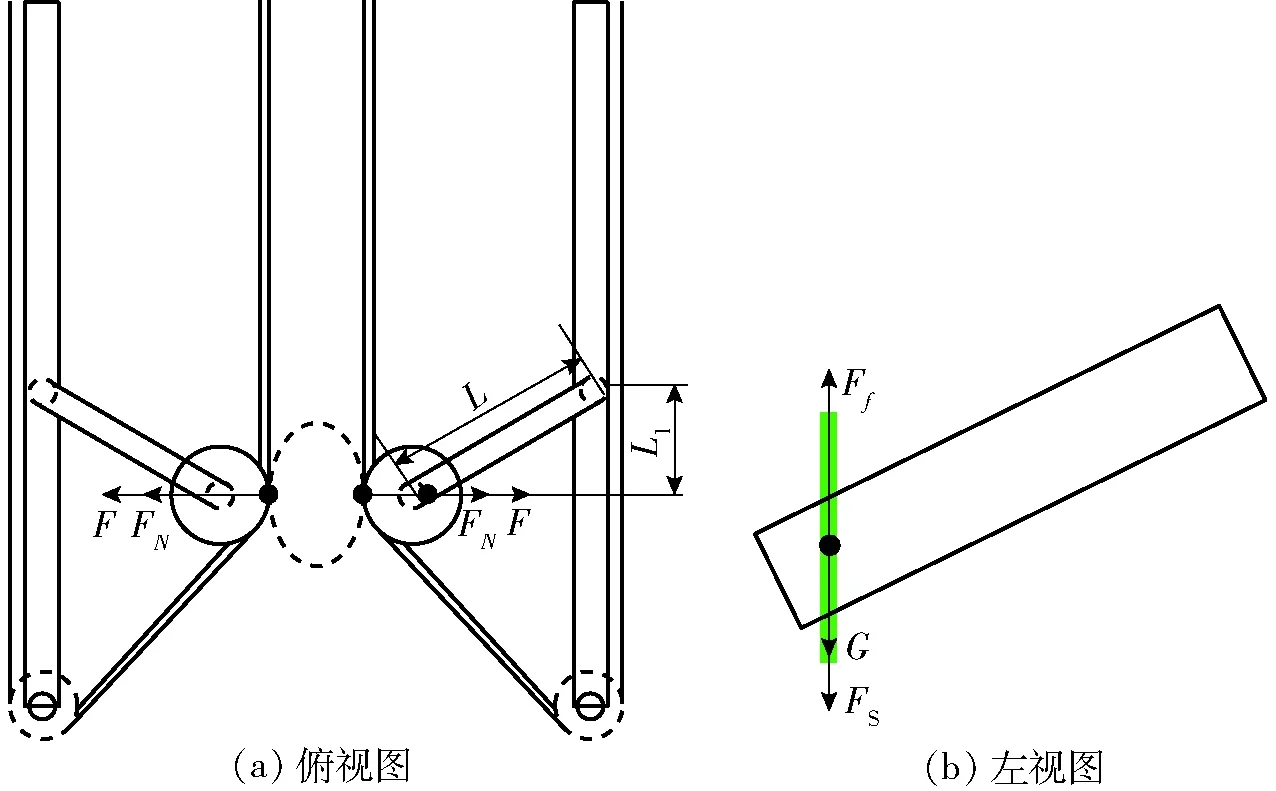
图5 浮动夹持过程受力分析Fig.5 Force analysis diagrams of floating clamping process
在浮动夹持过程中,菠菜变形量满足关系式
(6)
式中Dh——总变形量,包括菠菜变形量和扭簧变形量,mm
k0——夹持轮当量弹性系数,N/mm
F——夹持轮受到的菠菜作用力,N
浮动机构中扭簧产生的扭矩为
(7)
式中E——材料弹性模量,MPa
I——弹簧丝截面惯性矩,mm4
R0——扭簧中径,mm
n——扭簧有效圈数
扭簧产生的力矩为
M′N=FL1
(8)
式中L1——支撑杆两定位孔间沿着机架方向距离,为130 mm
通过式(1)、(7)、(8)可以得到夹持轮的当量弹性系数
(9)
由式(9)可知,k0与扭簧的参数、机构参数有关。
要保证菠菜顺利夹持输送,夹持力FN需要满足[16-17]
(10)
式中m——菠菜质量,g
γ——安全系数
μ——夹持带与菠菜的静摩擦因数
通过测量[18],菠菜与夹持带之间的静摩擦因数取值为1.9。
γ值为夹持机构提供给菠菜的摩擦力与夹持菠菜重力的比值,由于菠菜根部可能会粘附少量土壤,所以为了保证顺利夹持,需要满足γ>1;但是γ值越大,要求夹持力越大,越易产生损伤,综合考虑取γ=2。
2 菠菜流变数字模型
2.1 模型的建立
菠菜在采收过程主要受到挤压作用,果蔬作为粘弹性物料具有流变特性,因而菠菜植株在受到挤压作用时满足流变特性[19]。Burgers模型可以充分描述物料的流变特性,本文菠菜植株流变模型采用四元件Burgers模型,如图6所示。
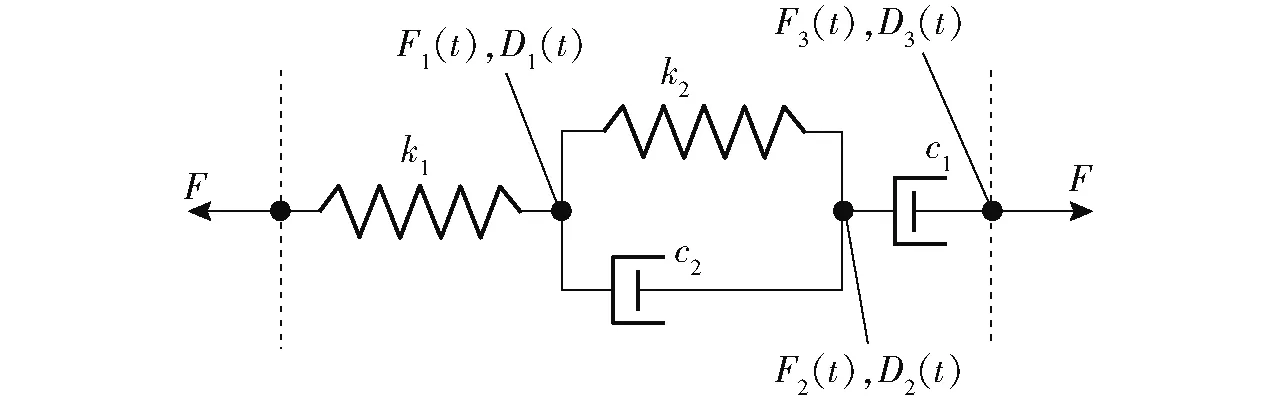
图6 Burgers流变模型Fig.6 Burgers rheological model
根据Burgers流变模型可以得到
F(t)=Fi(t) (i=1,2,3)
(11)
(12)
F1(t)=k1D1(t)
(13)
(14)
(15)
式中k1——瞬时弹性系数,N/mm
k2——延迟弹性系数,N/mm
c1——串联粘性系数,N·s/mm
c2——并联粘性系数,N·s/mm
对式(11)~(15)进行变换消掉Fi(t)和Di(t),求得菠菜流变的本构方程为
(16)
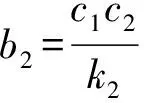
(17)
b1=c1
(18)
(19)
(20)
式中,本构方程系数a1、a2、b1、b2均为常数,可以由蠕变模型参数k1、k2、c1、c2求得。
将式(6)代入式(16)中求得菠菜浮动夹持过程本构方程为
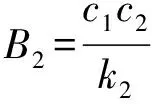
(21)
B1=c1
(22)
(23)
(24)
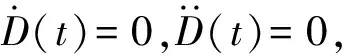
(25)
2.2 模型参数的获取
2.2.1蠕变试验
选取成熟期的大叶菠菜为试验对象,大叶菠菜茎叶柔嫩,收获过程极易产生损伤,其基本物性参数如表1所示。
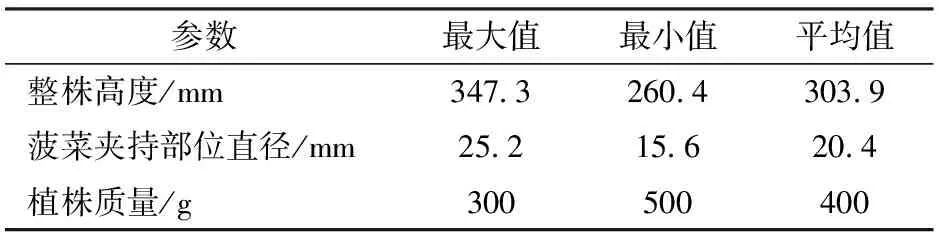
表1 菠菜物性参数Tab.1 Spinach physical parameters
将试验对象分为3组,每组10株,在TA-XT2i型质构仪上进行压缩蠕变试验,质构仪选用P50探头(直径为50 mm),如图7所示。

图7 蠕变试验台Fig.7 Creep test platform
具体的蠕变试验步骤为:试验探头的加载速度为1 mm/s,对3组菠菜分别施加2、3、4 N压缩力,保持力恒定,记录变形量随时间的变化关系。图8为不同加载力下菠菜的平均变形量随时间的变化曲线。
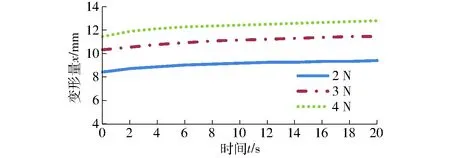
图8 不同加载力下平均变形量随时间的变化曲线Fig.8 Changing curves of mean deformation and time under different loading forces
2.2.2蠕变参数的获取
根据Burgers流变模型,由式(11)~(15)联立得到Burgers蠕变模型本构方程为
(26)
使用Matlab曲线拟合工具箱cftool进行曲线拟合,根据式(26)得到各加载力作用下相应的蠕变参数,具体拟合结果见表2。由表2可以看出菠菜蠕变模型参数的拟合决定系数均大于0.996,说明Burgers蠕变模型能很好地表示菠菜挤压蠕变特性,并通过3组试验的平均值求得蠕变模型参数。
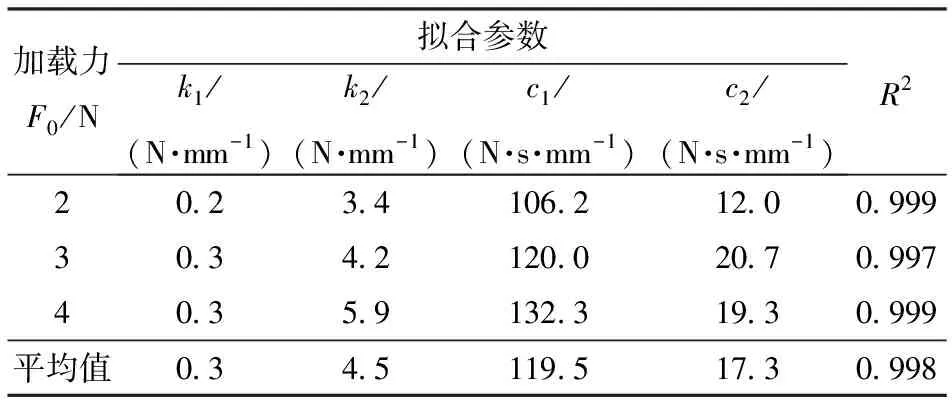
表2 菠菜蠕变模型拟合参数Tab.2 Fitting parameters of spinach creep model
2.3 菠菜损伤的表示方法
菠菜挤压过程的变形主要分为弹性变形、塑性变形和粘弹性变形,其中弹性变形卸去载荷后可以迅速恢复,粘弹性变形卸去载荷后可以缓慢恢复,而塑性变形卸去载荷后变形永久保存。塑性变形是菠菜产生机械损伤的主要原因,其变形量主要由串联粘性系数c1决定,塑性变形量计算式为
(27)
本文将塑性变形量作为衡量机械损伤严重程度的度量,菠菜塑性变形越大,越易产生机械损伤[20-21]。为了避免损伤,要求塑性变形尽可能小,通过塑性变形关系式对不同作用参数下菠菜机械损伤进行优化分析。
3 作业参数对菠菜损伤的影响分析
3.1 夹持轮当量弹性系数对菠菜塑性变形的影响
通过调节扭簧刚度调节螺栓的相对位置,可以改变夹持力大小,由式(9)求出此时的夹持轮当量弹性系数k0,当k0=5 N/mm,代入式(23)、(24)求得
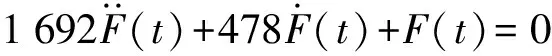
求解二阶微分方程得到
F(t)=I1e-0.002t+I2e-0.28t
通过试验求得初始条件F(0)=8.1 N,F(5)=6.8 N。代入求得I1=1.6,I2=6.5。求解得到夹持力与时间的关系为
F(t)=1.6e-0.28t+6.5e-0.002t
同理得到不同当量弹性系数下的夹持力随时间的关系式:当k0=1 N/mm时,F(t)=0.3e-0.28t+2e-0.001 4t;当k0=2 N/mm时,F(t)=0.9e-0.28t+2.6e-0.001 8t。
当输送速度为20 mm/s时,作用时间t=L/v2=22.5 s。
根据关系式得到夹持力随时间的关系曲线,如图9所示。
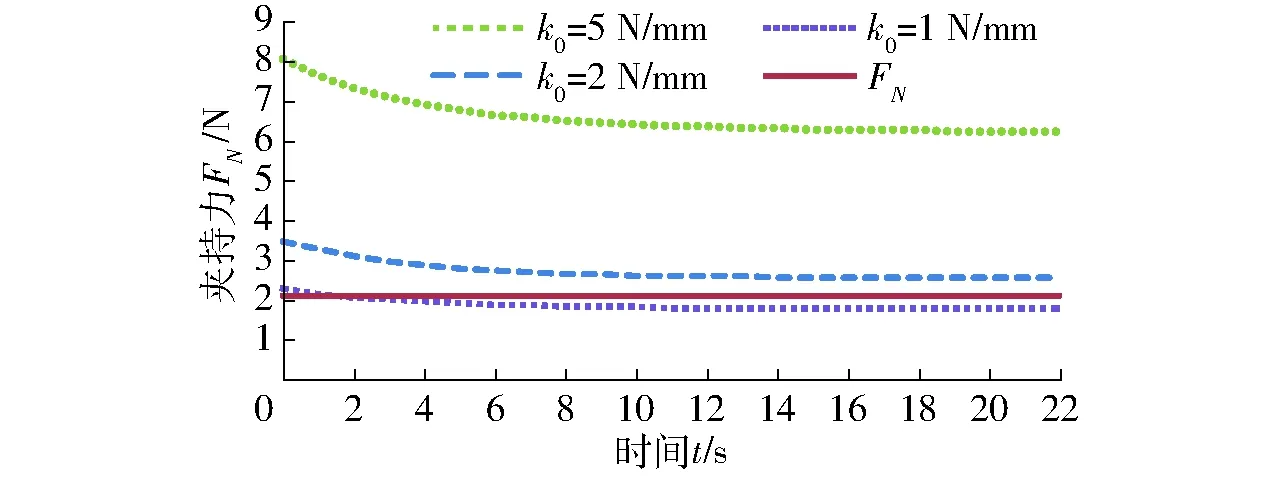
图9 不同当量弹性系数时夹持力随时间变化曲线Fig.9 Changing curves of clamping force and time under different equivalent modulus of elasticity
由图9可知,夹持轮当量弹性系数越小,菠菜受到的挤压力越小,由式(27)可知,菠菜产生的塑性变形越小,菠菜越不容易产生机械损伤。但是当夹持轮当量弹性系数过小时,根据式(10)求得菠菜顺利夹持输送需满足FN≥2.1 N,此时不满足夹持条件,在夹持过程中会发生脱落的现象。当k0=2 N/mm时,在满足夹持输送条件的前提下,夹持力最小,此时对应的塑性变形量最小。最小塑性变形量xp满足
3.2 输送速度对菠菜塑性变形的影响
菠菜夹持过程中的挤压速度v1与输送带的输送速度v2有关,由式(2)~(4)确定速度关系v2/v1=5。可知输送速度与夹持挤压速度成正比。此外输送速度还影响菠菜植株在夹持带中的作用时间,输送速度越大,菠菜在夹持带的输送时间越短,由式(27)知,塑性变形量越小。
在质构仪上对菠菜进行力学特性试验,当最大压缩量为10 mm时,发现不同挤压速度下菠菜植株受到的挤压力不同,速度越大,菠菜受到的挤压力越大,由式(27)可知产生的塑性变形量越大,菠菜损伤越严重。所以输送速度影响夹持力和作用时间的大小,进而决定塑性变形量的大小。为了减小挤压力,需要减小挤压速度,但是考虑到采收效率,输送速度不能太小,本文输送速度取v2≥20 mm/s。当v2=20 mm/s时,v1=v2/5=4 mm/s。夹持时间t=L/v2=22.5 s。
取k0=2 N/mm,代入式(23)、(24),并求解二阶微分方程得F(t)=0.9e-0.28t+2.6e-0.001 8t。
同理保持k0不变,考虑输送速度v2的可调性,分别取25 mm/s和30 mm/s,求得相应的夹持力方程为F(t)=3.1e-0.001 8t+1.4e-0.28t,F(t)=4e-0.001 8t+2e-0.28t。
得到不同输送速度下夹持力与时间的关系曲线,如图10所示。

图10 不同输送速度下夹持力与时间的关系曲线Fig.10 Relationship curves of clamping force and time at different transmission speeds
由式(27)求出不同速度下的塑性变形量。
当v2=20 mm/s时
当v2=25 mm/s时
当v2=30 mm/s时
当输送速度为25 mm/s时,塑性变形量相对较小。为了减小机械损伤,本文输送速度选择为25 mm/s。
4 试验验证
为了验证上述分析的正确性,搭建了菠菜夹持输送测试试验台,主要包括:夹持输送装置、菠菜输送带、升降调节装置、驱动电机,如图11所示。通过将菠菜根部插入到土槽中,放置在输送带上,模拟实际夹持输送过程。升降调节装置不但可以固定夹持输送装置,而且可以调节夹持输送装置的角度。驱动电机改变输送带的输送速度,可以模拟实际采收过程中输送装置在不同速度下的采收过程。调节浮动机构的扭簧刚度调节装置,改变夹持轮当量弹性系数。

图11 菠菜夹持输送测试试验台Fig.11 Spinach clamping conveying experimental platform1.大叶菠菜 2.夹持输送装置 3.升降调节装置 4.输送带 5.驱动电机 6.土槽
试验地点为山东省园艺机械与装备重点实验室,选择生长状况相同的成熟期大叶菠菜为试验对象。对试验台进行参数调节,夹持轮初始间距调节为10 mm,分别改变输送速度(20、25、30 mm/s)和当量弹性系数(1、2、5 N/mm),共进行5组试验,每组试验夹持输送30株菠菜,计算每组试验的夹持输送成功率P和菠菜的损伤率Q,计算式为
(28)
(29)
式中y——菠菜成功夹持输送的株数
z——用于试验的菠菜总株数
s——试验中损伤菠菜的数量
试验结果如表3所示,随着输送速度的增加,菠菜损伤率有所增加;随着当量弹性系数的增加,虽然输送成功率增大,但是菠菜的损伤率也相应增加。在当量弹性系数为1 N/mm时,虽然损伤率较小,但是夹持输送成功率却较小。综合考虑,当输送速度为25 mm/s、当量弹性系数为2 N/mm时,输送成功率为93.3%,菠菜损伤率为6.7%,夹持输送效果较好。
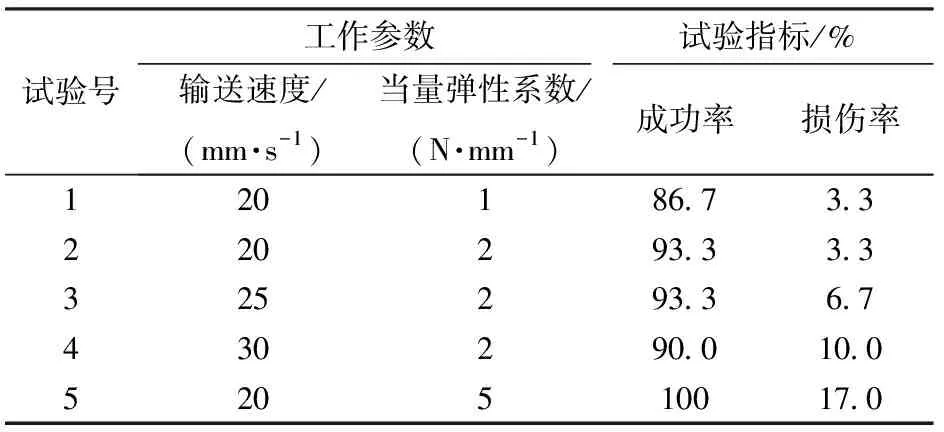
表3 试验方案与结果Tab.3 Experiment plan and results
由前面作业参数对菠菜损伤影响分析得到,随着当量弹性系数和输送速度的增加,菠菜的塑性变形量逐渐增大,菠菜的损伤率相应增加,但是当量弹性系数过小,由于夹持力小于临界夹持力会使菠菜输送的成功率降低。将分析结论与试验结果对比发现,试验结果与之前分析的结论一致,说明用菠菜流变特性来分析工作参数对菠菜的损伤影响是可行的。
5 结论
(1)基于Burgers模型构建了菠菜植株的流变本构模型。通过对菠菜植株进行蠕变试验,得到了在挤压力恒定的情况下,变形量随时间的变化曲线,通过与蠕变本构方程进行曲线拟合,得到了蠕变参数。将蠕变参数代入到菠菜流变方程中,求得最终的流变本构方程。
(2)以塑性变形量作为衡量菠菜机械损伤的评价指标。利用流变本构方程分别求得不同夹持轮当量弹性系数、输送速度情况下的夹持力与时间的关系式,分析了不同工作参数对菠菜夹持塑性变形的影响。通过分析得出,当输送速度为25 mm/s、当量弹性系数为2 N/mm时,塑性变形量较小。
(3)通过试验验证了试验结果与分析结果的一致性,证明了用菠菜流变特性分析工作参数对菠菜损伤的可行性。

