基于本质属性建构概念意义——以《相交与平行》教学为例

浙江省杭州市余杭区教育局教研室 李玉华

浙江省杭州市余杭教育学院 张建明

围绕“扎实·智慧的数学课堂——坚持与包容：基于基础性课程内容的数学核心素养培养”这一主题的浙江省杭州市2018年小学数学教学观摩评比活动已经圆满结束了，在此活动中我区推出的《相交与平行》，课后得到了同行们“简洁与深刻一致”的高度评价，并荣获了一等奖中的第一名，现将“起源、思考、实践、反思”的心智经历分享与大家。

一、起源

为了迎接市小学数学教学观摩评比活动，我们团队选择了人教版四年级第五单元《平行四边形和梯形》的第一课时《平行与垂直》作为了研究课例。

1.学生没有真正理解“同一平面内”含义

“在同一平面内不相交的两条直线叫做平行线”是人教版给“平行线”概念的定义。教材先让学生在纸上任意画两条直线，通过观察、分类、直线延长等画一画、分一分中逐步明确平行线概念，比较简洁、高效。但学习后“同一个平面”这一前置条件学生并没有真正理解。我们尝试让五年级的学生说说：“下图中两条直线是什么关系？为什么？”，绝大多数学生能说出“两条直线既不平行也不相交”，但能正确说出“为什么”则寥寥无几，更不知道两直线所在平面位置。

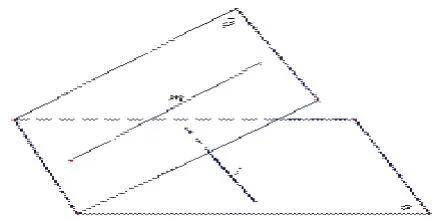
显然，从二维到三维的思维跨度较大，对学生的空间想象能力要求太高，事实上上图中直线m所在的平面可以有无数个，同理直线L也有无数个，但是不能合在同一平面内，这是很难让四年级的孩子去领悟的，所以教学时学生对异面两直线体会并不深刻，蜻蜓点水，浅尝即止，缺乏整体建构。

2.学生理不清“平行、相交、垂直”关系

人教版教材把此内容的课题定为《平行与垂直》，从教材的版面设计来看，对平行和垂直概念明显笔墨较多，有意无意地弱化了相交的地位，从以往的课例来看，一课时内完成相交、平行、垂直的教学是普遍现象，这样产生的副作用是：学生对三者之间的逻辑关系常常混淆。我们对不同教师任教的班级做了三次后测（结果统计如下表）。可见，教材着重突出了平行与垂直后，相当一部分学生对于三者之间的关系是不甚清楚的，将垂直概念与相交、平行置于并列关系占了27%。

题：请你用维恩图（集合图）表示一下同一平面内相交、平行、垂直之间的关系。

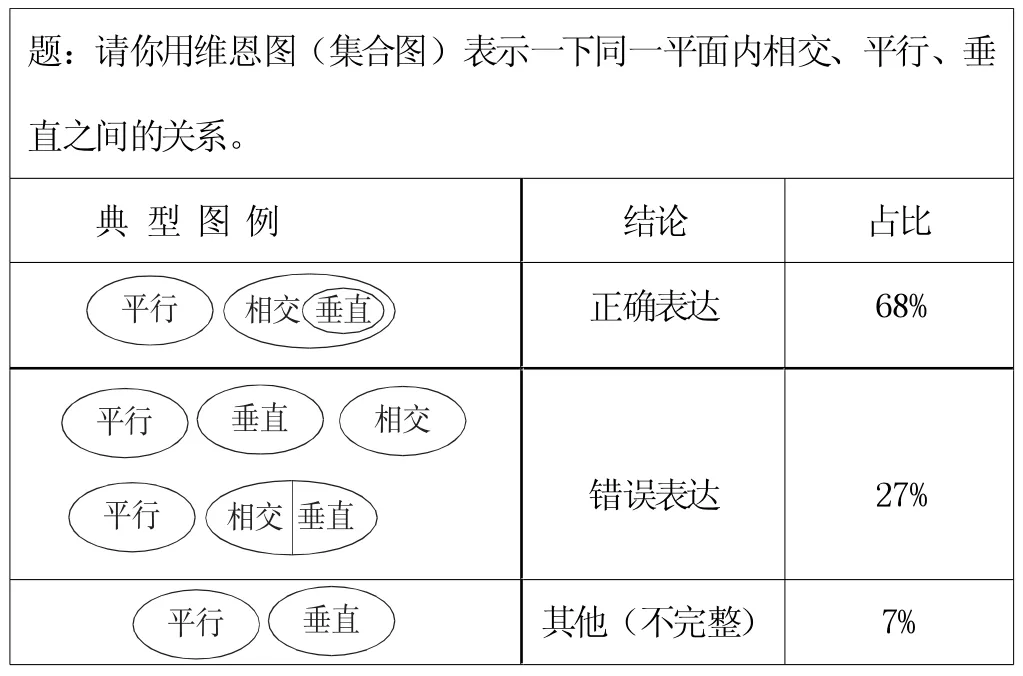
题：请你用维恩图（集合图）表示一下同一平面内相交、平行、垂直之间的关系。典 型 图 例 结论 占比images/BZ_61_289_640_417_710.pngimages/BZ_61_426_638_599_714.png正确表达 68%images/BZ_61_264_753_392_823.pngimages/BZ_61_400_750_527_820.pngimages/BZ_61_542_751_670_821.pngimages/BZ_61_271_847_399_918.pngimages/BZ_61_408_845_581_920.png错误表达27%images/BZ_61_335_954_463_1025.pngimages/BZ_61_471_951_598_1021.png其他（不完整） 7%

二、思考

为了突出教学重点突破教学难点，我们从基于本质属性建构概念意义的角度，对“同一平面内”含义真正理解的导入、“相交、平行”概念意义重构的定位、“教材再整合”课时安排调整的设想，进行了较深入的思考。

（一）基于“同一平面内”含义真正理解的导入

“同一个平面”的理解是本节课的难点，不同的学生在认知上存在差异，为了突破并强化“必须在同一平面内”的理解，是否可以尝试教学导入时就在一个三维空间内来研究两条直线的位置关系，再从三维到二维再到一维，反其道而行呢？理由是学生接触到的现实空间都是三维的、可视化的立体空间，比较符合认知习惯；二者在三维空间内研究两线关系，便于整体建构，将所有两直线位置关系一一呈现出来（包括同面、异面），再通过分类、比较、辨析，顺势引出相交与平行，而所用的三维空间的载体，就只需一个简单的长方体而已。

（二）基于“相交、平行”概念意义重构的定位

基于学生积累的丰富表象和学习经验，人教版教材对“相交”概念直接出示，没有下定义，如果在一个平面内讨论两直线关系，这当然是没有任何问题的，但如果对两直线关系在一个三维空间内讨论，两直线关系出现的情况会非常复杂，所以需要对“相交”的本质属性有一个简单的判断，考虑到四年级学生的实际，将“有交点”作为判定相交的本质属性。关于平行线，人教版教材给了比较严格的定义“在同一平面内不相交的两条直线叫做平行线”，这个定义更多的是基于对平行线的判定，而非平行线的本质属性，华东师范大学数学系张奠宙教授在《小学数学教材要厘清逻辑顺序——谈平行与平移》一文中指出：“‘平行线’教学要和方向概念联系起来，应用直线的方向相同来定义直线的平行。”基于这样的认识，将“方向一致”作为平行线的本质属性在教学中加以落实。

（三）基于“教材再整合”课时安排调整的设想

在《平行与垂直》一课时中教学完相交、平行、垂直，由于知识点较多，带来的一个问题是一部分学生对三者之间的并列与包含关系混淆，教学效果存疑。因此，从单元立意、整体建构的角度考虑，将“垂直”概念挪到第二课时进行教学，在本课时中聚焦于研究“相交与平行”的关系，课时安排调整的设想（如下表）。

版 本 第一课时 第二课时 第三课时 第四课时教材原编排平行与垂直画垂线 垂线段、平行线间距离处处相等画长方形、正方形整合后安排相交与平行垂直、画垂线垂线段、平行线间距离处处相等画长方形、正方形

三、实践

（一）画一画——感知两条直线的不同位置

师：同学们，请看这是什么？

生：长方体。

师：现在老师请你们在长方体上，用直尺和水笔任意画两条直线。

生：画两条直线（师以照片的形式展示“学生作品”，并用手比划只要“在这个长方体上画两条直线都可以”）

师：请想一想这两条直线你会画在哪里呢？（学生动手操作）

借助于长方体这个三维的工具，让学生在长方体面上任意地画两条直线，肯定会出现同面、异面的直线；相交、待相交、平行、既不相交也不平行等各种两直线关系，既可以为后续分类提供丰富的素材，也可以在一个三维的框架下整体建构两直线关系，目的是让学生感知两条直线的不同位置。

（二）分一分——思考两条直线的不同关系

师：巡视中将典型的7种画法借助西沃同屏软件拍照实时传于大屏幕。

师：如果让你给它们分分类，你会怎么分？把你的想法先说给同桌听一听。

（同桌交流想法，然后请学生上台拖动图片分一分）

生1：把两条直线画在同一个面上的分为一类（图①②⑥⑦），画在不同面上的分为一类（图③④⑤）。

生2：把交叉在一起的分为一类（图②③），不交叉在一起的分为一类（图①④⑤⑥⑦）。

生3：这两条直线延长后也会交叉在一起（图⑥），也应该分在交叉的那一类。

生4：我觉得这四幅应该单独分一类（图①②⑥⑦），它们在同一个面上。

师：听了这几位同学的意见，他们对这四幅图（图②③⑤⑥）有不同的想法，既然这样我就先来研究大家没有意见的这三幅图（图②③⑥）。

对这7种类型进行分类，根据前测发现学生分类的思考路径基本可概括为两种，第一种是按两条直线是否画在同一个平面上来分，第二种是按两条直线是否相交（学生称交叉）来分，但是这两种分类的路径，最终都会指向相交、平行、既不相交也不平行三类，所以分类的切入点不同，但出口端相同，殊途同归，目的是让学生自主思考两条直线的不同关系。

（三）议一议——理解相交平行的概念含义

1.基于“有交点”建构“相交”概念

师：先来看这幅（图②），这幅图你们都说这两条直线是交叉在一起的，那么它们在哪里交叉了呢？

生1：它们这样（用手比划）交叉在一起了。

生2：一条直线这样，另一条方向这样，不一样的就交叉了。

师：那哪个地方可以看出来因为它们方向不一样就交叉了呢？

生：这个点。（生上台指一指交点）

师：同学们刚刚说的交叉在一起，在数学上我们就说这两条直线的位置关系就是“相交”，这个交叉的点就叫“交点”，只要这两条直线有相交关系那么就会“有交点”（板书）。

师：那这两幅图（图③⑥）的两条直线相交吗？

生：相交。（图③）交点在棱上（学生上台比划）；（图⑥）交点在延长线上，因为这是直线，直线是可以无限延长的。

师：把掌声送给他，直线的特点马上就想到了。如果把这两条直线延长，那你能想象下大约会在什么位置相交（生想象）。

师：拿出直尺动手操作，实际证明这两条直线也会相交。这条直线向着这个方向延长，另一条直线向着另一个方向延长，最终它们相交了，交点就在这儿（比划）。我们把这三幅图移到黑板上。这些图中的两条直线都相交，相交后都有交点。

从没有争议的相交图入手，让学生指一指在哪里交叉，指向相交的本质属性“有交点”，同时随即渗透相交的两条直线“方向不一样”，为后面学习平行的本质属性“方向一致”做好埋伏。有了第一幅图关于相交本质属性“有交点”的准备，然后用这一属性来判断异面相交（本质上是同面）和延长后相交这两种情况，完善了对相交概念的认知。

2.基于“方向一致”建构“平行”概念

师：我们来看这两幅图（图①⑦），刚才同学们都同意这两幅图中的两条直线是不相交的，你们是怎么想的？

生：这两条直线方向是一样的，不管怎么延长都不会相交的。

师：那向左向右穿过这个屏幕无限延长下去呢？

生：还是永远不会相交的，因为这两条直线的方向是一样的，不会相交在一起的。

师：是啊（动态延长图①两直线），像这样的方向一样的两条直线永远不相交，我们就说这两条直线互相平行。它们的位置关系就是“平行”（板书）那这两条直线互相平行吗（图⑦）？说说你的想法。

生1：还是互相平行的，它们和前面图中两条直线一样的，只是都是朝着前后方向延长的，延长后也不会相交的。

生2：他说的就是两条直线向着前后无限延长永远不会相交的，所以也还是互相平行的。

师：是的，这两条直线向前、向后这两个方向无限延长，它们都是不相交的，所以它们是互相平行。那这样呢（旋转图⑦）？

生：还是互相平行的，只是现在两条直线都是向同一个方向斜着的。

师：对的，像这样延长方向一致的两条直线，永不相交，就互相平行了。

基于“方向一致”初步建构“平行”概念。由于没有学过垂直，无法用距离处处相等来判定，因此对平行的定义是基于视觉直观，即两条直线向两端无限延长之后也不会相交（借助于计算机技术和空间想象），落脚点是在“方向一致”上，通过前后方向，左右方向，旋转后斜向，体会平行的两条直线都是向同一个方向无限延长。

师：那这两条直线互相平行吗（图④）？

生 1：平行

生2：不平行

生 3：平行

师：谁来说说你们是怎么想的？

生3：前面说了只要方向一致的两条直线就互相平行了，那么这两条直线的方向是一样的，所以我认为这两条直线是互相平行的。

师：那认为不平行的你们又是怎么想的？

生2：这两条直线不在一个面上，也可以平行吗？

师：其实要互相平行的两条直线还要在同一平面上，请仔细观察这两条直线它们能放在同一平面上吗？（学生沉思）

生1：可以的，把长方体拆开来就好了

生2：拆开来打开就能放到同一平面上了

师：还有不拆的想法吗？（生没有其他想法）那你们先看动画（用刀沿着两条直线进行切割的动画），看完你再思考下你有没有新想法？

师：现在你看到了什么？

生1：经切割，这两条直线它们在一个面上了。

生2：这个面和我们平常看到的不一样，这个面是切出来的，而且还是斜着的。

生3：是的，只要是平平的就是平面了，斜着的也是的。

师：是呀，像这样方向一致的两条直线我们就可以切出一个斜斜的平面了，这两条直线就在同一平面上了，看来这三副图中的两条直线都是互相平行的。

基于“方向一致”深入建构了“平行”概念。先通过讨论图中异面（实质是同面）平行的两条直线来激发认知冲突，再把两条异面的直线想办法放在同一个平面上，是一个需要很强空间想象力的任务，学生的直觉思维是把这个长方体的面给拆了拉平。对于需要斜切在长方体内部来找平面的方法学生普遍感到困难，借助计算机辅助，动态演示切的过程，学生恍然大悟，难点顺势而解。

3.基于“同一平面”深化“相交与平行”本质

师：那这两条直线呢（图⑤）？

生1：属于相交的。

生2：应该是平行的。

生3：它们不会有交点，所以肯定不是相交。

师：刚刚第一位同学说相交的，请问交点在哪里？

生1：把这条直线延长就会在这里相交了（学生比划）。

师：真的？老师这儿有两根小棒咱们就把它们当成这两条直线，请你上来摆一摆看。

生1：上台摆好，硬生生把小棒折弯说相交了。

生：（抢答）这是直线怎么可以折弯呢？应该是不相交的。

生：（抢答）老师我还发现这两条直线方向是不一样的，而且也不在一个面上。

师：谁听懂这位同学说的了吗？

生：他说这两条直线的方向是不一样的。

师：那这两条直线是互相平行吗？

生：也不是平行。

师：是呀，像这样的两条直线不会相交，方向也不同，而且也不在同一平面上，所以它们“既不是相交也不是平行”（板书）。今天大家一起研究了两条直线的关系：相交与平行（板书）。像这样既不相交也不平行的我们以后再研究。

最后的图⑤是属于异面中既不平行也不相交的情况，它的存在对于完善相交和平行的概念有很大作用，由于拍成的图片是二维的，学生在辨析中存在困难，因此通过教具的直观演示（用两根小棒代替直线）来进行突破，效果较好。此环节还发生了一个学生将小棒折断后让线强行相交的小插曲，也很好地反证了直线必须是直的特性。最后点明本课主旨，研究的是两条直线之间的关系：相交与平行，相交的本质属性是两直线“有交点”、平行的本质属性是两直线的“方向一致”。

四、反思

1.课题演变有利于关系的简单理清

课题是一个“眼”，课题的演变及背后的思考（如下表）。从“教、学、评”的结果看，过程的思考是深刻的，课题的演变是正确的，它更有利于学生简单理清“相交与平行”的并列关系。

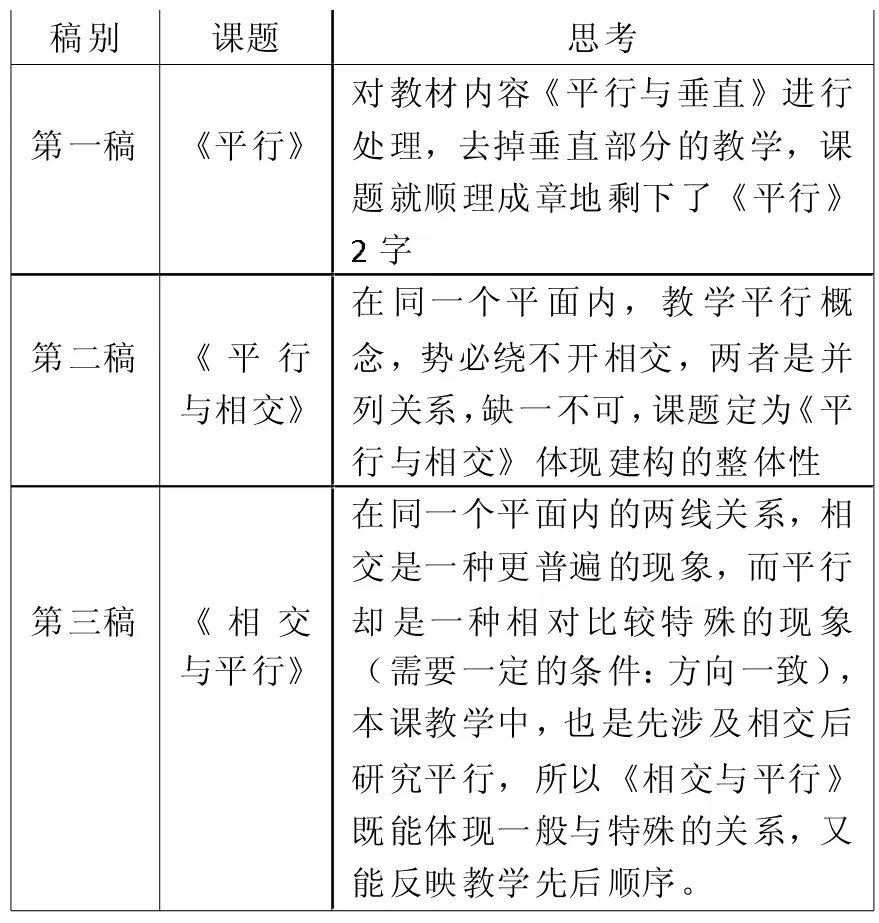
稿别 课题 思考第一稿《平行》对教材内容《平行与垂直》进行处理，去掉垂直部分的教学，课题就顺理成章地剩下了《平行》字第二稿《平行与相交》在同一个平面内，教学平行概念，势必绕不开相交，两者是并列关系，缺一不可，课题定为《平行与相交》体现建构的整体性第三稿《相交与平行》在同一个平面内的两线关系，相交是一种更普遍的现象，而平行却是一种相对比较特殊的现象（需要一定的条件：方向一致），本课教学中，也是先涉及相交后研究平行，所以《相交与平行》既能体现一般与特殊的关系，又能反映教学先后顺序。

2.本质把握有利于概念的深刻建构

从一个“体”上来研究两直线关系，即从三维整体构建再回到二维研究，对四年级学生来说虽具有一定的挑战性，但从课堂教学效果看学生由于生活经验的积累，空间想象能力还是能有效支撑的。关于“平行线”的定义不同版本教材有的“像这样……”描述性定义，有的“在同一平面内不相交的两条直线叫做平行线”下相对严格的定义，没有出现用“方向一致”这个角度来定义，是考虑到四年级学生的认知水平较低空间观念不足采取的不得已策略，还是另有原因我们虽不得而知，但从学生课堂学习结果看，基于“平行”的本质属性弱化“同一平面”用“方向一致”来建构概念意义还是切实可行的。当然，作为一堂研究型的课，颠覆以往固有的设计结构，提供一种全新的切入视角，一切还有待时间来检验。