汽车球铰的力学性能分析

鲍雨梅,2，周 威，潘孝勇3，吴 蕾3，吕 君

(1.浙江工业大学 机械工程学院，浙江 杭州 310023；2.浙江工业大学 之江学院，浙江 绍兴 312030；3.宁波拓普集团股份有限公司，浙江 宁波 315800)

球铰结构一般用在汽车转向系统上，具有三个旋转自由度。球铰的主要作用是确保汽车在行驶方向上的操纵稳定性、行驶平顺性、舒适性及安全性，故要求球铰具有一定的力学性能，如刚度、拉溃力和固有频率等。在球铰的设计阶段，必须保证球铰在承受拉压力时球销与球碗始终不相互分离。因此，须通过一系列的试验以及有限元分析来保证设计可靠性。其中，Martins等[1]利用有限元仿真软件对球铰拉溃力性能进行分析，从而预测了处在开发阶段的球铰类零件的拉溃失效行为。Baynal和Sin等[2-3]基于DOE方法研究了球铰零件的拔出力问题，一方面重新定义了球铰的球座和球销外径尺寸，另一方面通过重复五次的球铰拉出实验来确定拔出力以及球销焊缝处的强度。Kumar[4]通过有限元方法模拟控制臂在一定荷载和边界条件下的力学行为，利用试验获得其刚度和相应的应力状态。杨庆华等[5-7]基于Deform软件对零件的成形过程进行数值模拟仿真，分析其成形过程中的行程载荷与材料流动特性，并针对挤压过程中的变形抗力较大问题优化振动台的振幅值。由于本研究的球铰拉压溃力分析属于瞬态动力学范畴，短时间内无法体现金属的流动特性对拉压溃力的影响，故而不考虑球座材料的流动状态对球座收口处与球销在挤压过程的影响。另外，球铰在满足强度工况的同时还需要满足静刚度标准与NVH要求。Kang等[8]利用有限元分析方法及理论模型研究了轴向力、接触刚度等因素与球铰摩擦噪声之间的关联，若球铰的轴向力较大，在球铰摆动过程中易产生自激振动。除此之外，球碗的压力分布、球销的倾斜角度以及球头润滑状态都会影响自激振动的频率值与振型。因此，在球铰研究设计阶段需对其进行复模态分析，确保新产品不产生摩擦振动，从而排除球铰的异响风险。

1 球铰的拉压溃力计算分析

1.1 材料力学性能参数的确定

球销常用材料为牌号40Cr的合金钢，球碗的材料为聚甲醛(POM)，盖板的材料为牌号ST12，球座的材料为C20。按照GB/T 1040.2—2006和GB/T 228.1—2010测试规范，在岛津AG-IC100材料试验机上完成单轴拉伸试验，如图1所示。利用Matlab拟合数据变化趋势稳定点至最大拉力点间的数据，并获得相应材料的工程应力应变曲线。但在获取工程应力应变曲线的过程中，不考虑试样尺寸变化和试样发生颈缩的影响，所以工程应力应变曲线不能真实反映材料的本构关系，尤其在塑性变形阶段[9]。根据名义应力应变与真实应力应变之间的换算关系可得真实应力应变曲线，进而识别曲线上的屈服强度和抗拉强度，如表1所示。由于篇幅所限，以C20材料为例进行展示，如图2所示。

图1 材料试验机Fig.1 Material testing machine

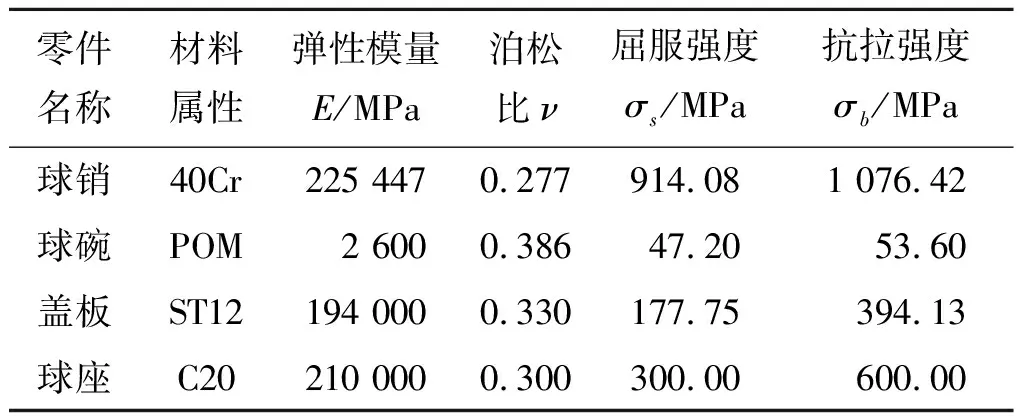
零件名称材料属性弹性模量E/MPa泊松比ν屈服强度σs/MPa抗拉强度σb/MPa球销40Cr225 4470.277914.081 076.42球碗POM2 6000.38647.2053.60盖板ST12194 0000.330177.75394.13球座C20210 0000.300300.00600.00

图2 20钢的应力—应变曲线Fig.2 Stress-strain curve of 20 steel

1.2 有限元分析与拉、压溃力试验

1.2.1 有限元模型的建立

首先，在Pro/E中建立球铰三维模型，将其Stp格式模型导入Hypermesh软件中进行网格划分。网格划分时针对球碗的不规则性，需进行多次几何处理，以保证整体单元质量。本模型采用C3D8R六面体网格类型，总计有34 616 个单元，43 062 个节点。接着，将表1所列的参数材料属性分别分配给球铰的各个零件。在对已生成的整体网格进行检测时，要求95%的网格的雅可比值大于0.6，以及应力集中区域的网格体积扭曲度小于0.2[10]。在本次仿真中，盖板与球座之间以及盖板和球碗之间只存在法向力，由于球座铆边处的尺寸约束并不会产生相对运动，故而将该接触副属性定义为光滑无摩擦。同理，球碗与球座之间不会产生切向位移，故为便于仿真操作将接触属性定义为光滑无摩擦。另外，不考虑温度、载荷和转速等因素对摩擦系数的影响，球销与球碗间的摩擦系数定义为0.15。在球心点处建立局部坐标系，且盖板中心点D与盖板底面绑定，球心点C与球销内表面采用REB2刚性耦合方式建立加载点，具体如图3所示。

图3 球铰网格模型Fig.3 mesh model of ball joint

1.2.2 拉、压溃力试验

利用MTS试验台对球铰进行拉、压溃试验，将球铰放在预制的工装中，施加一定的载荷，记录零件从开始受力到零件失效的整个拔出力/压出力曲线，如图4所示。本试验中的加载速度为100 mm/min，测试温度为(23±2) ℃。在拉、压加载状态下分别进行5 次试验，5 次试验取平均值，试验结果如图5所示。由于每次试验结果较为接近，为了更直观地看到拉压溃力随位移的变化趋势，对5 次试验结果分别进行平均化，拉、压溃力均值和位移曲线如图6所示。将5 次试验确定的拉、压溃力及位移汇总于表2。由表2可知：球铰分别在当Y向位移为2.85，2.28，2.20，3.43，3.78 mm时变形最大，产生的拉溃力分别为5.78，6.04，6.13，6.02，6.15 kN，平均拉溃力为5.98 kN；分别在Y向位移为5.62，5.76，5.79，5.94，6.07 mm时被压断，产生的压溃力分别为21.82，22.00，21.85，20.94，21.32 kN，平均拉溃力为21.89 kN。

图4 球铰拉压溃力试验Fig.4 The experiment under the condition of tension and compression

图5 球铰拉压溃试验结果Fig.5 The experiment results under the condition of tension and compression

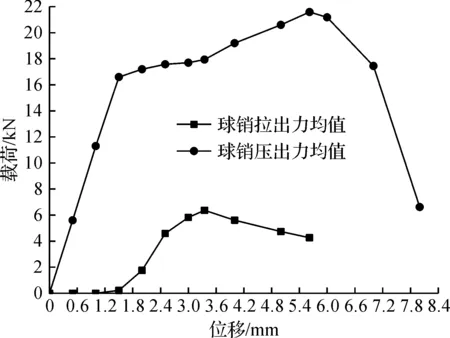
图6 球铰拉压溃力均值—位移曲线Fig.6 The mean of tensioning and crushing force-displacement curve

1.3 拉、压溃力有限元分析结果

横向稳定杆连杆球铰的拉、压溃力定义为球铰在分别受拉、压达到破坏时所能承受的最大载荷，即球铰在加载状态下达到最大应力后，继续加载时对应的加载力急剧减小的情况，此时的最大加载力即为拉、压溃力[11]。根据试验的加载规范与要求，在有限元分析模型的球销加载耦合C点上施加轴向±20 mm位移，后处理即可得到球铰轴向的支反力与位移之间的关系，进而确定拉、压溃力。在实际拉拔过程中，球碗POM材料因强度低变形大而受到破坏，而球碗上缘部分在仿真中因挤压而导致网格严重变形，这是仿真中存在的很大的一个缺陷，为了与实际更好地吻合，在显式动力学中可插入材料的损伤断裂准则，在仿真过程中可模拟材料的断裂。

图7(a)为轴向受拉的有限元计算结果，显示了球铰的拉溃点和此时的应力云图，其最大应力值已接近球座材料的屈服强度300 MPa，并且球碗的上缘部分因挤压而导致变形拉长，进而被损伤破坏，如图7(b)所示。图7(c)为轴向受压的有限元计算结果，球座的铆边附近的应力值都已接近材料的抗拉强度600 MPa。由图7(b，c)可知：球铰有限元计算结果与试验结果大致相同，都是收口部位被破坏。并且，通过调整球碗和球销的单元长度以及不同阶次单元，间接地验证计算结果的可靠性。拉压溃计算结果如表2所示。

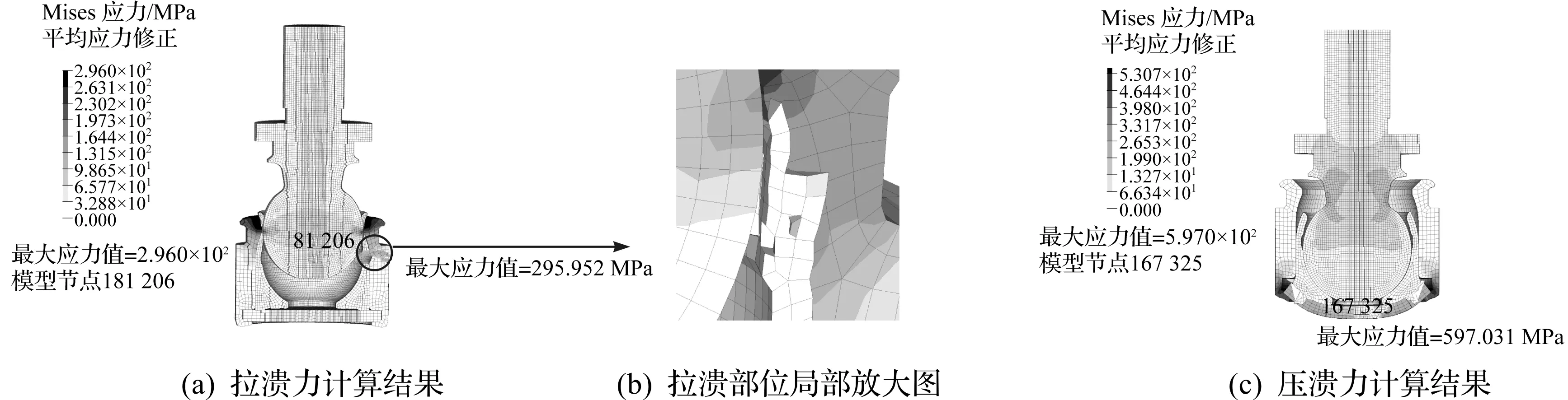
图7 球铰拉压溃力的分析结果Fig.7 The calculation results under the condition of tension and compression

表2 球铰拉压溃力试验值与分析值

Table 2 The calculation values and experiment values under the condition of tension and compression

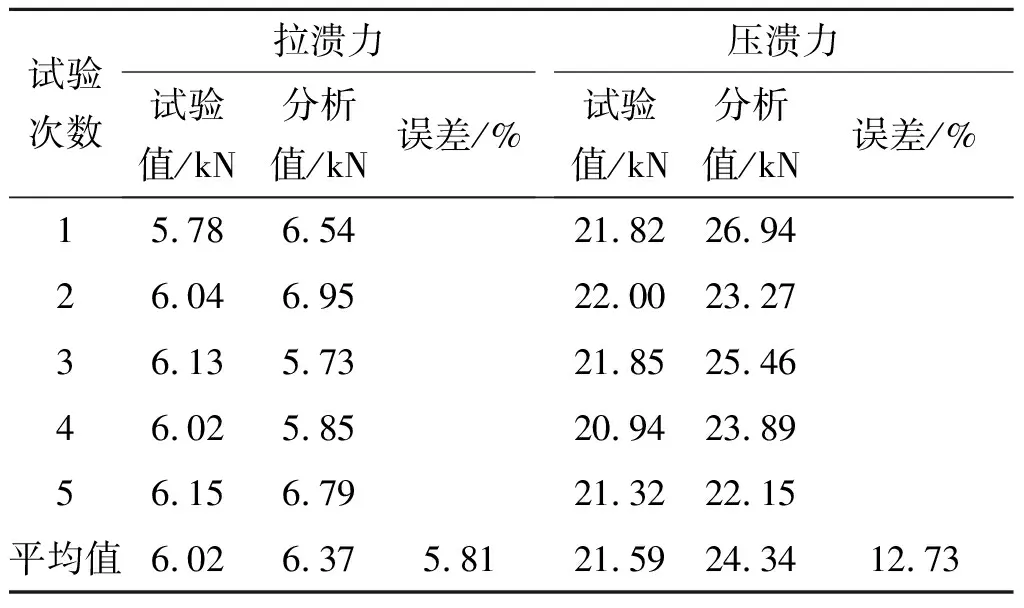
试验次数拉溃力试验值/kN分析值/kN误差/%压溃力试验值/kN分析值/kN误差/%15.786.5421.8226.9426.046.9522.0023.2736.135.7321.8525.4646.025.8520.9423.8956.156.7921.3222.15平均值6.026.375.8121.5924.3412.73

表2为试验值与计算值的对比。由表2可知：球铰拉溃力的试验结果与有限元计算结果基本一致。由于实际压装工艺中，球碗与球座、球碗与盖板之间存在不可避免的配合公差，导致有限元分析所得的压溃力值比试验值大。但压溃力分析值与试验值相对误差保持在15%以内，符合实际情况。

2 球铰的刚度计算分析

2.1 球铰的轴向与径向刚度试验

球铰刚度采用IAMT试验机进行测试，如图8所示。本试验的加载速度为(500±100) N/s，其中轴向加载1.2 kN及-0.5 kN；径向加载1.2 kN及-1.2 kN。测试次数为3 次，记录力—位移曲线，结果如图9所示。

图8 球铰刚度试验Fig.8 The stiffness experiment of ball joints

图9 球铰刚度试验结果Fig.9 The stiffness experiment results of ball joints

2.2 球铰的轴向与径向刚度分析结果

本球铰的刚度分析采用与拉压溃力分析基本相同的有限元模型。为了模拟垂直几何表面加载，在加载位置建立局部坐标系，方便在正确方向上施加载荷。根据径向刚度试验加载规范要求，在工装的内孔耦合点进行加载。利用ABAQUS软件通过有限元方法进行刚度分析计算，所得各加载位置的位移云图如图10所示。图10(a)中为球铰Y向受压时的位移云图，通过在工装内孔耦合点加载1 200 N，产生了58.48 μm的位移；图10(b)为球铰局部坐标系X向受压时位移云图，通过在球销上端耦合点加载1 200 N，产生了26.75 μm的位移。球铰刚度计算结果如表3所示。

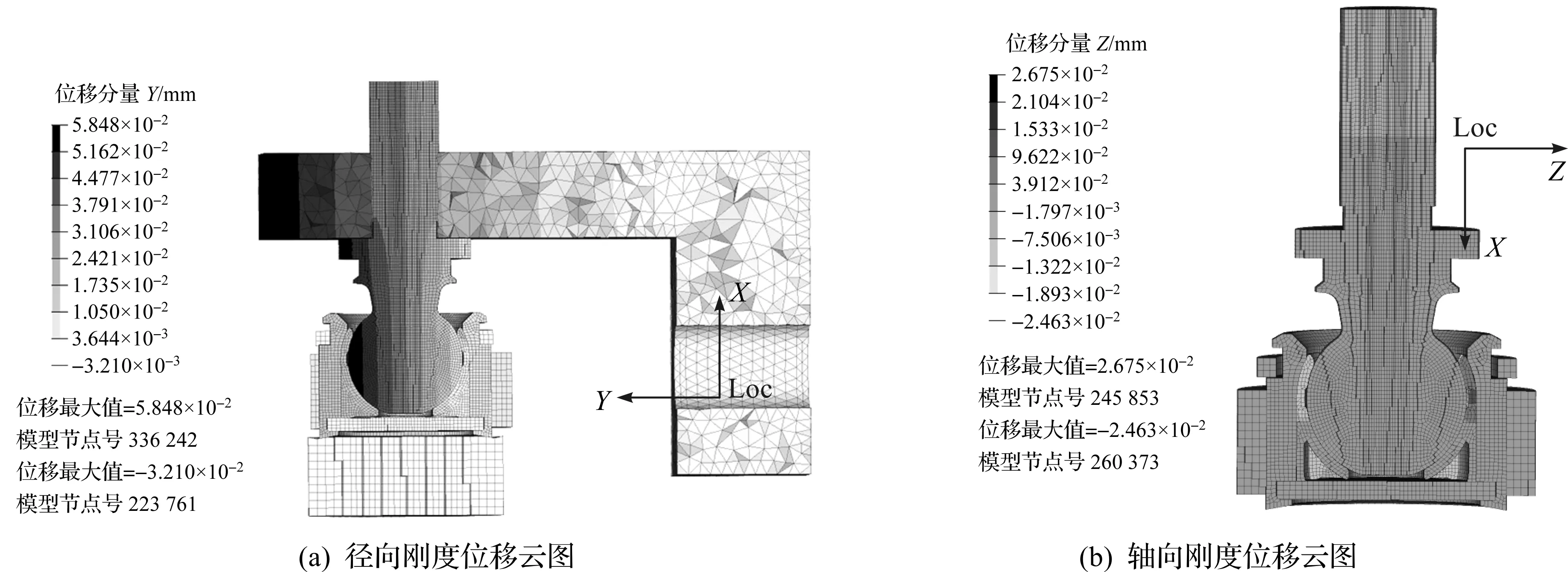
图10 球铰刚度位移云图Fig. 10 Displacement contours of ball joint

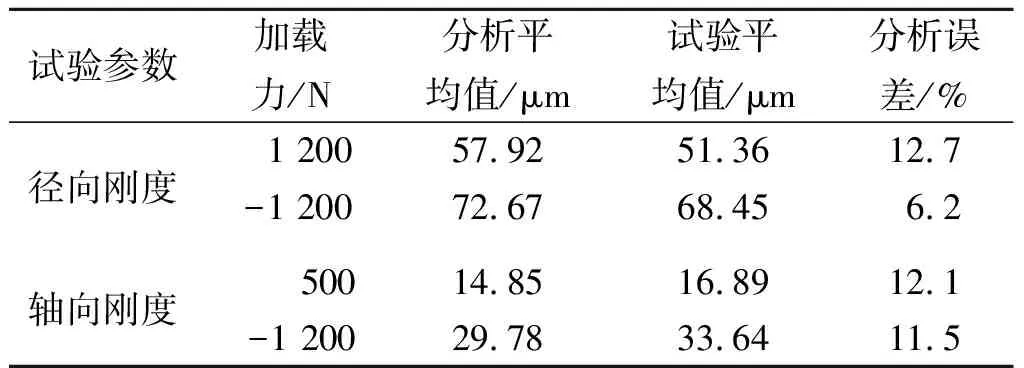
表3 球铰刚度计算结果Table 3 The stiffness calculation values of ball joints

表3为计算值与试验值的对比。由于球铰试件中的球碗和球座之间存在配合公差，导致径向过盈配合量会对测得的轴径向刚度值产生影响，但两者相对误差均保持在15%以内，说明了有限元分析结果具有可靠性。

3 球铰的复模态分析

3.1 复模态分析理论

目前国内外关于球铰摩擦稳定性的分析与研究并不多见，刘辉等[12]提到由模态参与因子和有效质量计算得到齿轮在各个振动方向上的主要振动模态以及各模态的主要振动方向，还得到系统在齿轮传动轴旋转方向上的振动是动力传动系统扭转振动的主要方向。杨龙等[13]在试件实验的基础上建立了盘式制动机构高频啸叫分析的复模态有限元模型，应用ABAQUS软件有限元分析软件计算了系统的复特征值。Kang[14]的研究表明，当球铰的摩擦状况处在速度与摩擦系数的曲线的负斜率段，接触面积以及球碗与球销的间隙量会影响球铰的稳定性。在本节中，通过复特征值分析法来分析汽车球铰产品的不稳定模态，以确定球碗与球销配合面间的摩擦力是否会激发球铰组件产生自激振动。

先建立有限元动力学方程，即

MX"+CX'+KsX=0

(1)

式中M，C，Ks分别为对称的质量矩阵、阻尼矩阵和刚度矩阵。法向的位移可以产生切向力(摩擦力)，摩擦力公式为

F=μKfX

(2)

式中：μ为摩擦因数；Kf为定义的非对称的摩擦耦合刚度矩阵。所以考虑了摩擦耦合后的有限元动力学方程变为

MX"+CX'+(Ks-μKf)X=0

(3)

因为加入了摩擦耦合刚度，使得刚度矩阵由对称矩阵变为非对称矩阵，因此系统产生了复特征值，从而导致了不稳定模态的出现。特征方程为

(Mλ2+Cλ+Ks-μKf)Φ=0

(4)

式(4)会产生一对共轭复数的特征值，μi=α±iβ，包含了自由振动频率β和振动阻尼α：当振动阻尼α为负值的时候，振荡会衰减，系统会最终达到稳定状态；当振动阻尼α为正值的时候，系统的振荡不但不衰减且最大幅值会随着时间的增大而越来越大，无法达到稳定状态，即有产生噪声的倾向[12-13]。

3.2 复模态分析结果

在ABAQUS有限元仿真软件中，若系统的刚度矩阵和阻尼矩阵是非对称的，则不能用常规方法进行方程解耦，这时必须用复模态法进行解耦。复模态的提取主要采用子空间投影法，提取复特征值就可以确定不稳定模态，因为复特征值的实部直接对应了不稳定模态。在本研究中，由于无法知道球铰产品的摩擦系数(下文所提及的摩擦系数是动摩擦系数)，因此需要利用CETR-UTM摩擦磨损试验机进行销盘摩擦试验，其中球头材料为下试样也即圆盘，球碗材料为上试样也即圆柱销，如图11所示。为了保证测得的摩擦系数的准确性，试样的表面粗糙度也与球铰保持一致。同样，为了排除Stribeck效应对球铰摩擦系数的影响，需要在平板试验中施加与扭矩试验相一致的滑动速度。由于球铰扭矩测试的角速度为10 (°)/s，则线速度V=ωR=0.1π rad/s×10 mm=3.14 mm/s。根据销与圆盘旋转中心的距离换算可得，旋转速度为15 r/min。另外，通过施加不同载荷来改变接触压强值，进而确定接触压强对摩擦系数的影响。为了能够更直观地得到摩擦副在干摩擦与脂润滑状态下的摩擦系数，需对数据进行降噪平滑处理，如图12所示。

图11 摩擦磨损试验机及试样Fig.11 Tribo tester and specimens

图12 不同摩擦状态下的摩擦系数—时间曲线Fig.12 Friction coefficient-time curve under different friction conditions

由图13可知：POM与40Cr材料在干摩擦状态下的摩擦系数随着载荷的增大，前期减小后期较为稳定，且处于0.15～0.2范围内。同理，脂润滑状态下的摩擦系数处于0.05～0.08范围内。由于实际装配过程中，球碗与球座处于过盈配合，导致其间产生较大的压强值(笔者不详述过盈量对球铰接触压强的影响)。本次分析中球碗与球座接触面的摩擦系数取0.15，球碗与球销的摩擦系数取0.08。在复模态分析过程中，先在球销耦合点Y向上施加50 N的载荷，然后以1 rad/s绕Y轴转动。分析中设置球碗与球销的摩擦系数μ1=0.08，其他接触面的摩擦系数μ2=0.15。笔者提取了前五阶的复模态频率，结果如表4所示。

图13 球铰组件的模态振型(前5阶)Fig.13 Mode shapes of ball joints

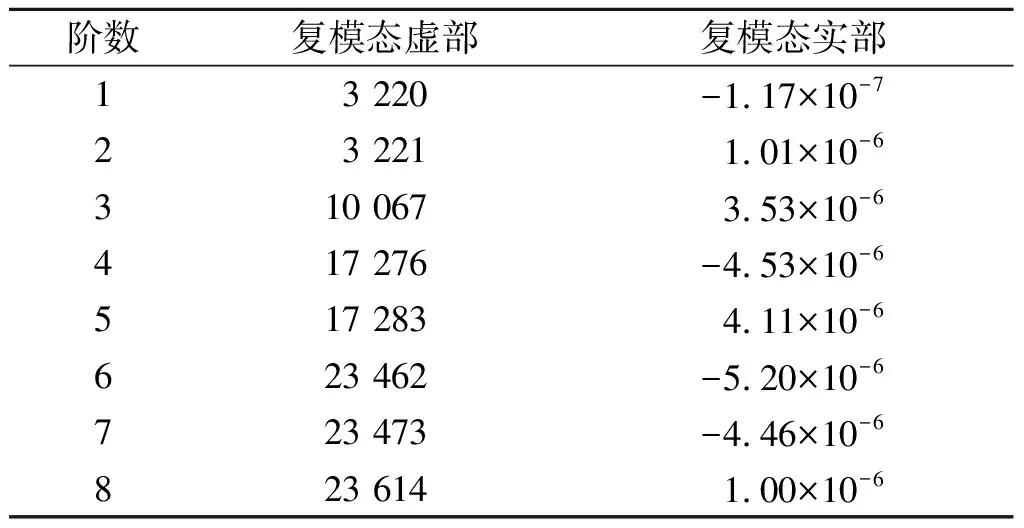
表4 复特征值的提取(前8 阶)Table 4 The extraction of complex eigenvalues

由表4可知：各模态特征值的实部值近似等于零，无不稳定模态。

4 结 论

针对球铰组件的各类材料，采用单轴拉伸实验方法获取力学性能参数。利用有限元分析软件对球铰的拉压溃力与刚度进行计算，分析结果表明拉压溃力与轴径向刚度皆符合主机厂的规范要求。其次，抽样选取若干个汽车稳定杆连杆进行多组拉压溃力试验与刚度试验，试验结果表明球铰的拉压溃力与刚度亦符合要求且证明了有限元分析方法的可靠性。最后，基于ABAQUS软件对球铰进行复模态分析，分析结果表明该球铰无不稳定模态，且稳定性较好。基于模态耦合机理产生的摩擦噪声是一个较为复杂的现象，目前笔者仅仅从有限元分析方面去作预测，并没有利用试验从球铰的摩擦性能以及各种极限工况下进行验证，也没有考虑润滑脂的黏度等参数以及球铰的过盈量与结合面的接触压强的关系等问题对球铰摩擦振动的影响，还需更进一步的研究。