基于几何基元定标的单幅图像组合式建筑建模
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
在计算机视觉和计算机图形学领域,针对建筑物三维模型的重建一直是研究的热点,该研究方向在智慧城市建设、虚拟现实与文化遗址数字化保护等领域有着广泛的应用[1]。对于需要专业建模知识的建模方法无法满足普通用户的建模需求[2]。传统的三维建筑物建模方法主要有过程式建模[3-4]、基于点云的建筑物建模[5-6]和基于图像的建筑物建模[7]等3 类。相较于前两种方法,基于图片的三维重建技术通过输入图像提取并计算三维信息进行模型重建[8],有效地回避了三维场景的几何复杂性,但同时在几何准确性和三维信息完整性上存在缺失与限制,从而给三维建筑物的重建带来许多困难,近几年来基于单幅图像建筑物模型重建方法的研究力度相较于前两种方法更具有研究意义与挑战性。在基于单幅图像的建筑物建模中,现有方法主要利用输入图像中提供的特征点和特征线、或者几何体的对称以及重复结构约束等信息,通过求解场景相机参数完成定标[9]或根据建筑物表面的几何约束关系来恢复三维信息[10]。Arikan等[11]提出基于建筑照片重建三维模型,建模过程中需要用户手动交互不断改进自动算法的结果。吴康乐等[12]提出了一种基于特征线素的轻量级三维建筑交互建模方法,称为fe-wires方法。该方法是一种基于形状文法的过程式建模方法,通过间接地输入和操纵建筑对象的特征线条来重构模型。Zheng等[13]提出通过匹配图像和数据库建筑物模型之间的轮廓实现建筑物建模,该方法避免了相机标定使得计算量大大减少,但由于数据源有限仅能处理简单的建筑物,无法应用于形状复杂的建筑物模型。郭美莉等[14]提出基于灭点计算利用摄像机标定模型建立建筑物三维模型,改善和扩大了建模需要的几何信息恢复,简化了建模过程。近年来,研究发现在可以分解为简单几何体的建筑物建模对象中,基于参数化几何基元的建模方法也成为新的研究热点,Zheng等[15]提出一种长方体代理的思想,将场景中的建模对象用长方体表示,通过用户交互提取并计算三维场景信息完成目标对象的模型重建,并将其应用到图像的交互式编辑方面。对于基于单幅图片的组合式三维建筑物重建技术,现有的三维重建方法通常需要复杂的用户交互和较大的操作难度,或者在追求简单交互的同时牺牲算法的计算量。
对于单幅组合式建筑图像的模型重建,已知组合式建筑即由多个规则几何体组合而成,每个几何体称为建筑物部件,组合式建筑各部件之间通常存在着大量的遮挡、共面和邻接等几何关系。现实生活中的大部分建筑如写字楼、居民楼和教学楼等均由长方体、圆柱体组合构建而成,对于该类组合式建筑图像,现有的建模方法往往需要输入图像的限制或大量繁琐的用户交互过程[16]。为解决这一挑战,实现交互简单、效率高效的三维模型重建,笔者提出了一种基于圆柱体和长方体几何基元定标的单幅图像组合式建筑交互式建模方法,对于不同部件采取单独建模最后联合优化完成准确的场景估计与整体模型的重建的方式,实现更为逼真的三维模型效果。笔者方法的主要贡献在于:1) 提出了一种基于不同几何基元定标的三维组合式建筑建模方法。对于长方体部件,采用基于平行六面体的相机标定技术计算相机内外参数及长方体尺寸信息完成场景估计并生成模型;对于圆柱体部件,通过用户交互提取两组平行线(即过底面圆心的长方形横截面长宽两组平行线),计算灭点后基于灭点进行相机标定并重建圆柱体部件模型。2) 结合各个部件单独完成的场景估计,基于单幅图像成像一致性进行场景估计的联合优化,最终计算出精确的场景估计参数并优化组合式建筑模型各部件的组合构建。与以往基于单幅图像的建筑物建模方法相比,笔者使用的建模方法旨在覆盖大部分由不同几何体构建的单幅组合式建筑图像的建模,通过对输入的单幅图像进行少量的交互处理进行相机标定,以重建出结构较为复杂的三维组合式建筑物模型。
1 三维组合式建筑重建方法流程
笔者提出的基于几何基元定标的单幅图像组合式建筑交互式建模方法首先通过对单幅输入图像进行少量的用户交互,针对不同类型的几何基元采取不同的建模方法,提取出相机标定所需的二维点线信息完成场景定标的各个参数求解并单独建模;然后结合组合式建筑各部件之间的共面、邻接等几何约束关系,建立误差函数与能量函数优化场景参数,实现场景的精确构建,最终完成组合式建筑的整体建模工作。这种方式的建模在一定程度上减少了计算量,并且大大减少了用户交互的操作。其方法流程如图1所示。

图1 方法流程图Fig.1 Algorithm flow chart
笔者方法主要包含如下步骤:
1) 基于几何基元定标的部件建模。针对由圆柱体和长方体组合构成的单幅组合式建筑图像,采取对各个部件采用不同标定方法进行单独定标与建模的策略,完成组合式建筑每个部件的模型重建。对于长方体部件,用户标注三维长方体部件顶点投影在二维图像上形成的六边形的6 个角点,系统利用这些角点与三维几何体之间顶点的对应关系构建长方体几何基元,使得长方体基元与二维图像上的部件轮廓相匹配,创建长方体部件模型并计算出相机内外参数;对于圆柱体部件,采用用户交互方式标注二维图像上圆柱轮廓的2 条高与2 个端面圆的4 个切点,系统提取圆柱体的两组母线轮廓线后计算3 个轴方向上的灭点。然后根据灭点进行相机标定,利用角点与三维圆柱体之间端点对应关系绘制圆柱体模型。
2) 基于联合优化的组合式建筑几何构建。系统在对各个部件进行场景标定与建模时,分别以每个部件的底面中心设为原点单独建立世界坐标系;计算出场景参数后,根据组合式建筑部件之间邻接面的几何约束关系并辅助以二维图像上用户标定的角点坐标与系统生成的三维模型投影二维点的距离误差,引进能量函数优化相机参数,生成场景估计,最终生成更为精准的建筑模型。
3) 利用纹理贴图技术完成纹理贴图完成模型重建。为了使得模型更加逼真,需要对模型进行渲染。在使用图像作为纹理过程中,由于拍摄角度以及组合式建筑各个部件之间存在的客观遮挡关系需要对纹理图像进行修补并完成最终的纹理渲染,生成最为精确和逼真的模型。
2 基于几何基元定标的建筑物部件建模
基于对单幅组合式建筑图像的观察,可以发现大部分组合式建筑都由2 个或2 个以上的规则几何体邻接组合而成。主要针对由长方体、圆柱体组合构建的单幅组合式建筑作为重建模型的对象,实现该类组合式建筑的建模。
对于单幅图像的组合式建筑,充分利用组合式建筑各个部件的规则几何体提供的三维信息,对各个部件进行单独的参数估计与建模,大大简化了用户交互,提高了对于该类建筑物的建模效率与质量。针对不同的建筑物部件,采取不同的定标方法完成对每个部件的参数估计与建模,充分利用不同几何体本身的几何特性使得计算量得到有效减少。
2.1 基于长方体几何基元定标的模型部件重建
在组合式建筑的三维建模中,针对其中的长方体部件,笔者提出以长方体几何基元作为对组合式建筑建模的基本元素之一,实现基于长方体标注的相机标定和长方体部件建模。用户交互式标注出长方体对象投影在二维图像上的6 个角点,系统捕捉这些顶点并利用其与三维几何体之间的对应关系构建长方体几何基元。由于相机拍摄的单幅建筑物图像中建筑主体在图像中占绝大部分面积,投影在二维图像上的成像往往会有透视失真的情况,为解决歧义,用户需要标注能覆盖长方体6 个面的6 个角点。如图2所示,在相机标定里,设置世界坐标系原点为长方体底面中心,坐标轴与长方体边对齐,为实现用户标注区域与世界坐标系中的长方体部件的二维投影图像区域相匹配,利用Wilczkowiak等[17]提出的基于平行六面体几何约束的相机模型计算出相机内外参数和长方体的尺寸参数l1与l2。

图2 相机标定Fig.2 Camera calibration
由图2可知:对于用户标注的兴趣区域Ri和长方体几何部件的6 个角点,建模目标是让长方体部件模型与区域Ri的二维图像轮廓相匹配。为建立相机成像模型,利用常见的相机投影矩阵相机模型为
M=K[R|t]
(1)
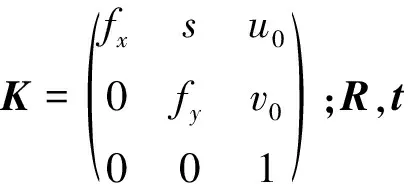
畸变参数s设置为0,世界坐标系为均匀坐标系,即fx=fy=f。至此,在长方体几何基元部件相机标定阶段需要计算的参数包括相机内参、相机外参以及长方体模型的长宽l1,l2。利用齐次坐标,投影矩阵映射每个长方体角Pi对应于图像上的二维点pi,表示为
pi=MPi
(2)
利用6 个对应关系Pi↔pi,使用动态线性规划方法(DLT)求出相机标定的11 个参数K,R,t,l1,l2。在完成相机标定后,根据式(2)计算出在世界坐标系下特征点的三维坐标,并利用三维点坐标绘制长方体部件模型,建模效果如图3所示。

图3 长方体部件建模效果图Fig.3 Modeling performance of cuboid component
2.2 基于圆柱体几何基元定标的模型部件重建
基于单幅图像的摄像机标定方法,其原理都是根据图像中长方体结构中线、面之间平行垂直的几何特征进行场景估计的,而对于组合式建筑中的圆柱体几何部件的模型重建,这种几何特征很难有效获取。因此,在针对圆柱体部件的建模和相机标定上,采取一种新的几何方法确定相机参数与建模。该方法主要利用圆柱体底面与侧面的垂直关系,通过用户交互,在三维圆柱体投影到二维图像上的矩形轮廓上标注出2 组相互垂直的平行线,计算2 组平行线的灭点,再利用透视投影理论中灭点的几何性质计算出相机的内外参数,从而实现相机标定(图4)。
具体地说,如图4所示,用户标注圆柱体部件二维图像上投影的轮廓两端面圆的顶点,得到2 条母线轮廓线ac,bd,至此可计算出轴向方向上的灭点v1。相机主点设为图像中心点。由图4可知:用户标注的4 个点即是该2 条母线与上下2 底面圆的切点,连接对应切点a,b和c,d得到轴线方向上垂直的2 组平行线,计算出另1 个方向上的灭点。利用主点p0的性质即主点是以3 个影灭点为顶点的三角形的垂心,可求出第3 个灭点v3。
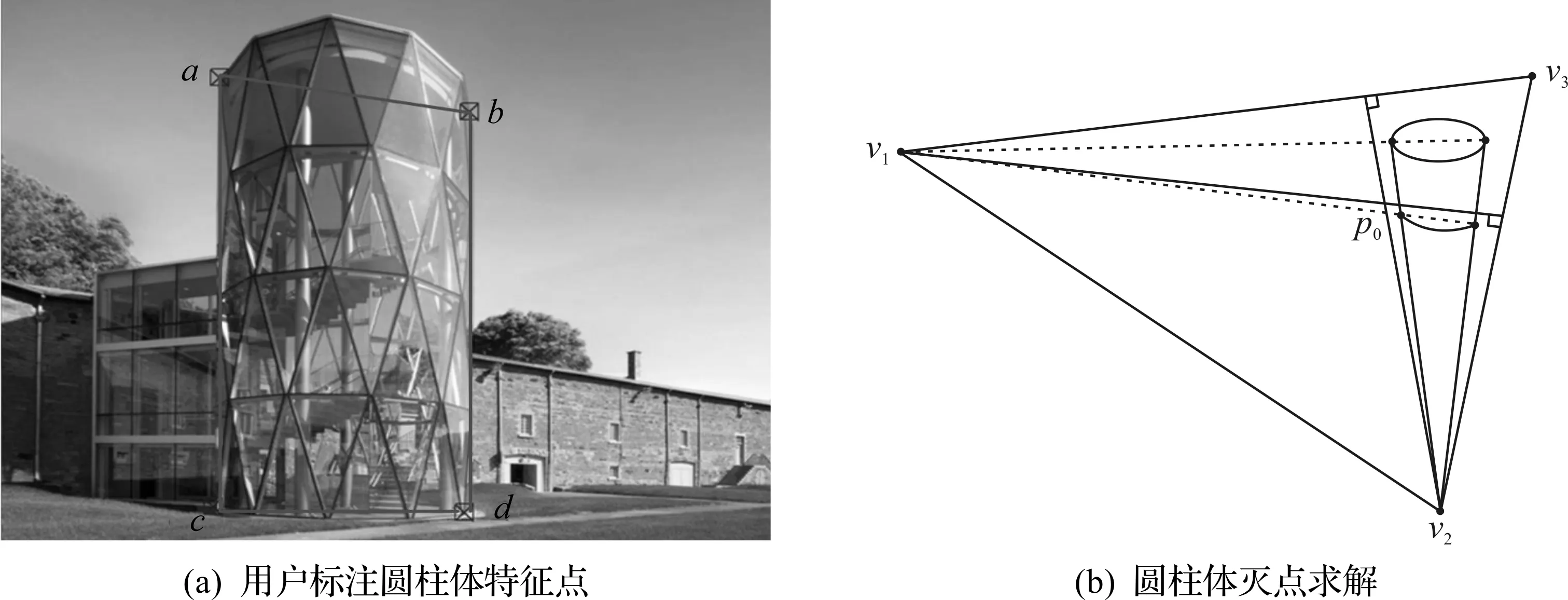
图4 圆柱体标注与灭点求解Fig.4 The cylinder label and vanishing points calculation
在计算出3 组相互正交的平行线所对应的3 个灭点图像坐标后,可求取相机标定的内部参数。已知3个灭点坐标为(ui,vi,1)T,i=1,2,3,它们对应的空间齐次坐标分别为(1,0,0,0),(0,1,0,0),(0,0,1,0),则相机内参与未知非零因子λi约束关系可表示为
(3)
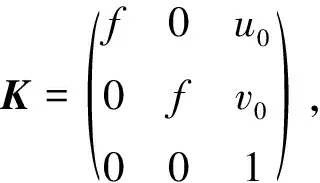
(4)
式(4)分解后可化为6 个线性参数方程,由该6 个参数方程求解出相机的3 个内参以及非零常数因子。
求解出相机内参与度量因子后,可将求解出的参数代入式(4)中,已知K,则可分解求出旋转矩阵的值。指定世界坐标系的原点在圆柱体底面圆心处,根据用户标定的底面圆端点求中心点的图像坐标(u4,v4),代入式(2)即可求解出平移向量。
完成相机标定的参数求解后,确定圆柱体几何部件的尺寸参数(半径r以及假设圆柱体高为单位长度)。则用户标注的点在世界坐标系下的坐标分别为(±r,0,0),(±r,0,1)。利用二维图像点到三维空间映射关系即可求解出r。至此,基于圆柱体的相机标定与模型重建完成。
3 基于联合优化的组合式建筑几何构建
在对单个几何体部件进行建模时,系统对每个部件建立单独的坐标系并独立计算相机内外参数,为使得组合式建筑各个几何部件的组合关系更符合二维图像提供的信息,需要生成统一且精确的场景估计。
由于单幅组合式建筑物图像各个部件之间存在邻接共面几何约束关系,利用该约束关系并辅助以用户标注角点坐标与系统生成的三维模型投影在二维图像上的二维点的距离误差,引进能量函数优化相机参数,生成最优场景估计,绘制更为精确的建筑模型。
在圆柱体几何部件与长方体几何部件邻接组合中,由于重合部分该部件在二维图像成像上往往只呈现出部分圆柱体。为了更好地避免由于重叠遮挡关系带来的几何模型拟合误差,在联合优化部分需要用户交互标注出长方体部件之间、圆柱体部件与长方体部件邻接的截面4 个顶点。系统获取用户标注的顶点坐标代入误差函数中进行计算。
假设用户标记的共面关系的面为Fi,i=1,2,…,n,定义关于建筑物长方体部件三维顶点Pij(i=1,2,…,n;j=1,2,…,6)和圆柱体部件特征点Oij(i=1,2,…,n;j=1,2,3,4)的误差函数为
(5)
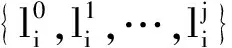
(6)
因此,共面约束误差可表示为
(7)
在计算过程中,如果T的值越小,那么相应的误差函数就越小。
利用误差函数,系统对生成的所有部件模型进行联合优化操作,将其转换为同一坐标系下的模型组合。运用Levenberg-Marquardt非线性最优化方法进行参数优化求解出最优参数,分别以场景中的各个几何基元计算出与其相对应的基元集合,并在结果中选出误差最小的1 组基元集合作为最佳结果进行三维绘制显示。
4 实验结果及讨论
笔者方法已经在3.40 GHz Intel(R) Core(TM) PC机上的Microsoft visual studio 2010平台利用C#进行了编程实现。系统使用NET平台下的Emgucv和OpenGL库实现目标物体建模。其中使Emgucv进行图像处理,利用OpenGL渲染生成的三维模型以及后续的纹理贴图。根据单幅输入图像,用户直接在图像上对长方体部件进行六边形角点标注,对圆柱体部件进行特征点标注,系统实现实时高效的建模效果。在重建过程中,用户无需具备专业的建模技术知识储备,只需根据二维图像进行简单交互即可快速生成三维模型。
图5给出了利用笔者重建方法实现的若干实例,其中图5(a,d,g)为输入的单幅图像,图5(b,e,h),图5(c,f,i)分别为不同角度模型效果图。由图5可以看出:对于具有2,3,4 个部件的建筑或者邻接面位于左右、前后等不同方位的组合式建筑,均能实现高效率的三维模型重建。实验表明:在整个建模过程中,在用户交互标注几何基元部件环节耗费的时间较多,在用户标注角点信息后,系统可以实时地生成粗略模型,用户可根据效果进行角点微调,使得用户交互误差尽量小。

图5 三维建筑物建模效果Fig.5 3D architecture modeling
为了验证该建模方法的有效性,我们请一些没有专业建模技能的同学通过简单的学习来使用笔者建模系统进行组合式建筑的建模,可以得到如图5所示的建模效果。第1 个建筑具有2 个部件, 有1 组共面关系, 用户标定用时46.32 s, 系统生成模型用时3.88 s;第2 个建筑共有4 个部件, 具有3 组共面关系, 用户标定用时58.22 s, 生成模型用时5.23 s;第3 个建筑具有3 个部件,具有2 组共面关系,用户标定用时47.00 s,生成模型用时4.53 s。整体平均建模时间在2 min以内,大部分同学认为该建模系统简单快捷且容易操作。笔者方法在用户交互过程中能够实时显示生成的三维模型。
图6给出了基于长方体和圆柱体几何基元定标的组合式建筑重建方法与Zheng等[15]提出的基于长方体交互式建模方法的比较。可以看出:Zheng等[15]方法根据用户标注的每个分割区域对每个长方体做六边形标注,一方面该方法对于圆柱体对象无法实现建模,且生成的模型与输入图像投影差距较大;另一方面,由于Zheng等[15]方法仅仅是根据用户对每个长方体对象进行标注,对于遮挡关系较多的组合式建筑物单幅图像,由于被遮挡部件的6 个角点信息的缺失,用户无法实现精确的标注,Zheng等[15]方法提取的几何关系往往与二维图像提供的信息相差较大。笔者方法不但可以同时实现圆柱体和长方体两种类型几何体部件的模型重建,且考虑了组合式建筑本身具有的各个部件之间邻接共面关系,运用几何约束可以实现更为精确的三维模型重建。
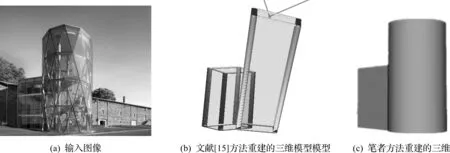
图6 模型重建方法比较Fig.6 Comparison of model reconstruction methods with existing work
图7给出了笔者方法与Zheng等[13]提出的基于模型库建模方法的比较,由于Zheng等[13]所建立的模型库较小,对于由圆柱体和长方体组合而成的复杂组合式建筑物图像匹配效果欠佳,利用笔者方法可以实现结构复杂的组合式建筑模型重建。对于简单的长方体建筑,Zheng等[13]通过模型匹配从数据库中可找到与输入图轮廓大致符合的粗略模型(图7b),而笔者方法重建的模型更加接近输入图像的真实效果(图7c)。此外,Zheng等[13]提出的方法虽然是系统自动匹配模型,不需要人工交互,但以牺牲模型真实性为代价,建立的三维模型与输入图片有一定误差。与Zheng等[13]的基于模型库建模方法比较,笔者方法建模对象覆盖面更加广泛、算法性能高以及能够实时高效地完成结构复杂的组合式建筑图像的三维建模。
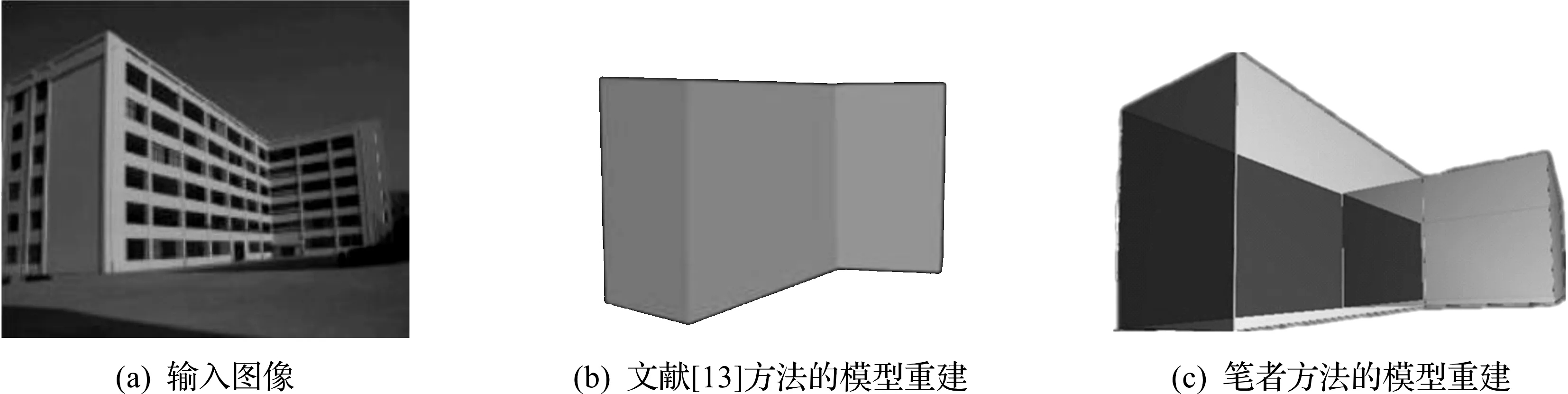
图7 笔者方法与基于模型库匹配方法的效果比较Fig.7 Effect comparison of 3D model reconstruction between ours and database-based method
5 结 论
针对由规则长方体与圆柱体组合而成的单幅组合式建筑物图片,提出了一种基于几何基元定标的单幅图像组合式建筑建模方法。该方法针对不同类型的几何体部件,采取不同的场景定标方法计算相机内外参数以及几何体尺寸参数并完成建模。然后对生成的各个部件模型进行基于共面邻接几何约束关系的联合优化,实现建筑物模型的精确重建。最后,根据单幅建筑物图像提供的纹理信息对生成的模型进行纹理渲染,完成与二维图像信息一致的组合式建筑物建模。实验表明:笔者方法不需要用户具有专业的建模知识,只需少量简单的用户交互即可完成建模,建模过程操作简单、建模效率高和实用性较强,可以满足现实生活中大部分组合式建筑单幅图像的建模需求。后续工作可以加入诸如球体、圆锥体多种几何体基元实现更为复杂的组合式建筑模型重建。

