基于多目标扰动观测器的不确定机器人滑模自适应轨迹跟踪控制*

刘树博，刘国权，周焕银，罗先喜，杨 波，江思懿

(东华理工大学 a.江西省新能源工艺及装备工程技术研究中心；b.机械与电子工程学院，南昌 330013)

0 引言

机器人是一类具有高度非线性、强耦合性和时变性的系统，且在工作中会受到所在环境、摩擦、负载扰动等因素的影响，因此机器人是一个典型的非线性不确定系统，其精确的数学模型往往难以得到，给机器人轨迹跟踪控制带来了一定的困难。

针对机器人的跟踪控制问题，国内外学者进行了大量研究，并取得了一些显著的研究成果[1-5]。滑模控制是一类特殊的非线性控制，对系统模型的不确定性和外界扰动具有高度的鲁棒性，已被成功应用于机器人跟踪控制中。文献[6-7]提出了基于神经网络补偿的滑模变结构控制，增强了系统鲁棒性，达到了良好的跟踪效果。文献[8]对机器人轨迹全局滑模鲁棒自适应控制进行研究，仿真结果表明了该算法的有效性。文献[9-10]提出了一种自适应滑模轨迹跟踪控制器，成功地解决了系统中未知参数、外界扰动和负载给机器人带来的不利影响。

到目前为止，大量的机器人控制策略，都是在系统动力学及其相关信息已知的前提下进行的。然而在实际工程中，机器人特性往往无法精确获取，甚至是完全未知的，使原有控制策略无法有效执行，从而降低了其实用性和有效性。因此，研究一种实用性较强，不依赖于机器人先验信息的控制策略，具有十分重要的意义。

扰动观测器技术，可用于逼近系统中的不确定干扰，对抑制机器人系统扰动和增强系统鲁棒性，起到了促进作用[11-12]。结合滑模控制和干扰观测器的各自优点，本文将二者相结合，以不确定机器人为研究对象，利用系统可测输出，提出一种不依赖系统先验信息的非抖振滑模自适应控制策略，通过与已有算法进行比较，进一步验证了该算法的实用性与有效性。

1 机器人轨迹跟踪问题描述

考虑具有n个关节的刚性机器人系统，其动力学方程可描述如下：

(1)

(2)

式中，x=[x1,x2]T∈R2n×1为系统状态变量；

f(x,t)=-M-1(x1)·[-C(x1,x1)x2-G(x1)]∈Rn×1；ω(x,t)=-M-1(x1)·Γ(x1,x2,t)∈Rn×1；

b(x,t)=M-1(x1)∈Rn×n。

机器人是典型的非线性不确定系统，在实际工程中获取其精确的模型难度较大，即便是标称模型也是十分难得。因此，设计一种新型实用的数学模型，对机器人跟踪控制问题的研究，具有十分重要的意义。鉴此，将模型(2)进行修改，可得如下形式：

(3)

其中，kc为待定时变正数，

d=ω(x,t)+f(x,t)+[b(x,t)-kc]u(t)为n×1阶集总扰动向量。

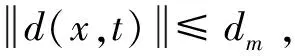
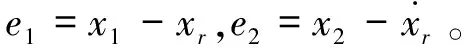
(4)

本文研究的问题可描述如下：为机器人系统设计滑模控制规律，考虑所有的外界扰动和内部不确定性，设计不基于系统先验信息的滑模自适应控制律u，使得对于任意初值(e1(0)，e2(0))，当t→∞时，e1→0且e2→0，使机器人关节实现对给定信号的跟踪。

2 滑模跟踪控制器设计

为了实现机器人的轨迹跟踪控制，本节首先根据机器人轨迹跟踪目标，设计出合适的切换函数，其次基于切换函数设计扰动观测器来实现对扰动向量的估计，最后基于Lyapunov方法设计自适应滑模控制器，实现机器人关节对给定信号的有效跟踪。

2.1 滑模控制律的提出

设计以下复合滑模面s：

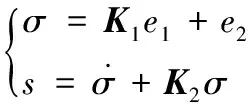
(5)

其中，In为n阶单位矩阵；s∈Rn×1，K1=k1In∈Rn×n，K2=k2In∈Rn×n；k1>0，k2>0为待定常数。将式(4)代入式(6)，可得：

(6)

假设2 ：给定期望跟踪轨迹xr光滑，且其三阶导数存在。

对式(6)进行求导，可得：

(7)

假定系统(4)的状态变量可测，采用指数趋近律，基于式(7)设计得到滑模控制律如下：

(8)

(9)

式(8)是一个关于控制输入u的微分方程，通过对不连续切换项进行积分运算，可对抖振现象起到了较好地抑制效果。

2.2 多目标扰动观测器的设计

2.2.1 观测器结构设计

在控制律(8)中，由于存在扰动估计向量，因此设计扰动观测器是十分必要的。设计扰动观测器结构如下：

(10)

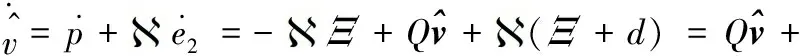
(11)

基于式(11)，进一步推导可得：

(12)

(13)

2.2.2 观测器多目标设计方法

(14)

引理2：根据极点配置理论[14]，系统(13)的闭环极点处于Θ(qc,ra)中，当且仅当存在2n阶对称正定矩阵Σ2，满足以下不等式

(15)

基于定理1，最优观测器矩阵Q*可以通过求解以下优化问题获得：

minρs.t. 式(14～15)

(16)

多目标设计方法兼顾了观测器的稳定性和动态性能，与已有报道[15-16]相比，具有更加优异的动态性能。

对于优化问题(16)的求解，有以下两方面值得注意：首先，Q由矩阵T和F相加而成，其特殊结构并不利于直接利用LMI方法进行求解。其次，在Σ1=Σ2的前提下进行求解，势必会给求解带来一定的保守性。因此，针对具有特定结构的矩阵Q，采用一种非保守的求解方法，是十分必要的。本文采用了将差分进化算法和LMI相结合的方法，对其优化问题(16)进行求解，获得的最优观测矩阵为Q*=arg infρ。算法具体步骤详见文献[17-19]，流程图如图1所示。

图1 求解算法流程图

2.3 滑模自适应控制律设计

定理2:针对机器人系统(1)及复合滑模面(5)，选取滑模控制律(8)及以下自适应控制律：

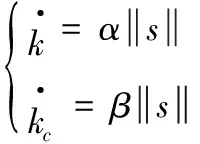
(17)

式中，α和β为自适应学习率。若控制律(8)中的切换增益满足条件ks=kc+k+ε，其中ε为任意正数，则跟踪误差系统(4)全局渐进稳定，即t→∞时，系统的位置跟踪误差e趋近于零。

(18)

对V进行求导可得：

(19)

将式(9)代入式(19)中，可得:

(20)

再将式(17)代入式(20)中，可得

(21)

3 仿真分析

将本文控制算法应用于双连杆机器人中[20]，其状态方程如下：

(22)

仿真中需要设定参数如下：首先，选取qc=200和ra=40，使用MATLAB中的LMI工具箱求解优化问题(17)，可得最优观测器矩阵为：

其次，滑模面参数为K1=K2=4I2；最后，自适应率选为α=0.03，β=0.01，ε=0.5。

文献[20]基于机器人回归矩阵模型，利用新型的Nussbaum函数设计了自适应跟踪控制律。为了进一步说明控制效果，与文献[20]的方法进行对比，仿真结果如图2、图3所示。从图中的对比可以发现：在本文算法控制下，机器人关节响应速度更快，且具有更小的稳态误差，因此能够更好地实现对给定信号曲线的跟踪，达到了更好的控制效果。由于本文算法只以系统输出信号为反馈，不依赖系统的模型结构，因此具有更强的实用性。

图2 关节1位置及速度跟踪误差曲线

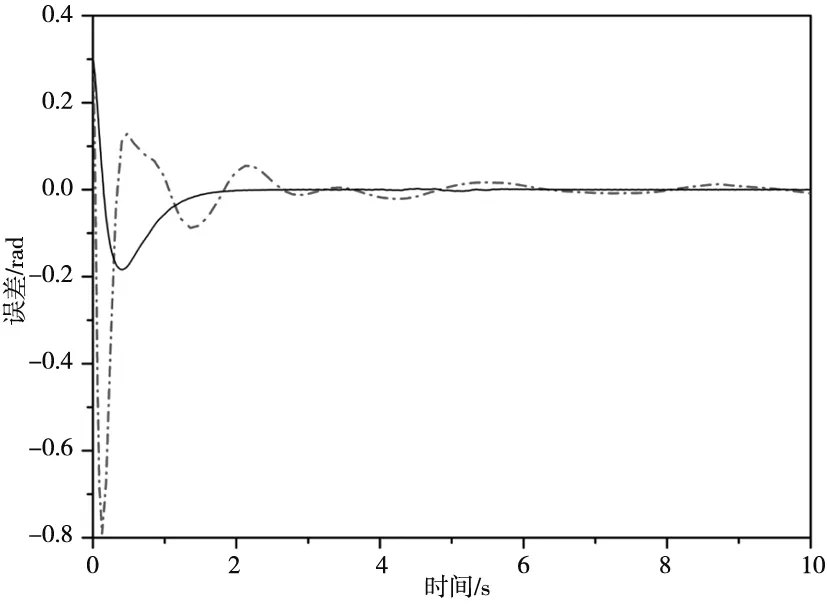
图3 关节2位置及速度跟踪误差曲线

4 结论

以非线性不确定机器人为研究对象，使用多目标扰动观测器逼近系统的建模误差和不确定干扰项，在此基础上研究了非抖振滑模自适应跟踪控制策略，并通过Lyapunov方法设计了自适应控制律，确保了系统的全局稳定性。最后，通过与已有文献的结果相比，验证了所提控制策略的实用性和有效性。