基于损伤缺陷激励的滚动轴承振动机理分析*

董绍江，贺 坤，汤宝平，张潇汀，王 艳

(1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆大学 机械传动国家重点实验室，重庆 400044；3.重庆交通大学，重庆 400074；4.重庆电力设计院有限责任公司，重庆 401121)

0 引言

滚动轴承作为重要的基础零部件，广泛应用在各种旋转机械中，其运行状态直接影响到整个机械设备的运行状态。因此，引起轴承的振动各种激励一直都是研究的重点。Harris[1]提出了球轴承拟动力学模型，且建立了轴承运动微分方程，但该模型没有考虑到油润滑作用，故无法准确反映轴承的振动特性。杜秋华等[2]建立了2自由度的球轴承非线性振动模型，并对球轴承振动的非线性微分方程组进行了简化求解。M S PATIL[3]和Ahmad Rafsanjani[4]等建立了滚动轴承二自由度非线性动力学模型，对局部缺陷在轴向和径向的振动响应进行了分析。杨将新等[5]建立了滚动轴承在低速运转下的内圈局部缺陷的轴承振动模型，并对其进行了仿真。周智等[6]提出了一种损伤缺陷模拟方法，建立考虑损伤缺陷因素引起球轴承振动的七自由度动力学模型。张耀强[7]等考虑轴承外圈局部缺陷等非线性因素，建立了动力学微分方程，分析了滚动轴承非线性动力特性。N Tandon[8]分析了轴承在轴向和径向施加载荷的作用下，内圈、外圈或滚动体发生局部损伤产生激振力时其振动响应及频率成分。M S Patil等[9]建立基于局部损伤缺陷的轴承振动频谱的分析模型，研究局部损伤缺陷对球轴承振动的响应情况的影响。胡亮等[10]分析了深沟球轴承外圈局部损伤状态下和正常状态下振动信号的特征。本文在滚动轴承理论研究的基础上，先建立滚动轴承动力学模型，并通过仿真得出轴承的固有振动属性，然后列出损伤缺陷激励导致轴承振动的激励表达式，最后通过试验分析内圈局部缺陷对轴承振动信号的影响。

1 滚动轴承动力学方程建模

1.1 滚动轴承钢球-滚道接触副弹性接触刚度矩阵和阻尼矩阵

本文采用摩擦力学与结构动力学相结合的摩擦动力学的方法，在干接触模型的基础之上，考虑油膜的刚度和阻尼，确定滚动轴承的刚度和阻尼。

在滚动轴承中，油膜厚度与轴承尺寸相比要小得多，因此钢球在法向接触载荷作用下沿Y轴滚动时，根据弹流润滑理论中描述润滑剂状态的雷诺方程，可表示为：

(1)

且边界条件为：

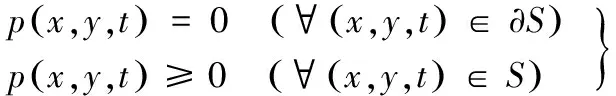
(2)

式中，p=p(x,y,t)为油膜压力，h=h(x,y,t)为油膜厚度，η=η(x,y,t)为润滑剂的动力粘度，ρ=ρ(x,y,t)为润滑剂的密度，vs为接触物体表面速度之和，S为接触区域。

并利用summerfeld条件化简，可得到钢球-滚道接触副的接触刚度和接触阻尼表示为：

(3)

(4)

其中，sc为钢球-滚道接触副的Hertz接触刚度，sf为Hertz接触区的油膜刚度。

钢球与内外滚道同时接触时，钢球的两端同时形成两个接触副。根据复合刚度方程式可以求得阻尼和接触刚度为：

(5)

(6)

式中，R(ω)和I(ω)分别为：

式中，i、o分别表示内外套圈，ω表示旋转频率。

在轴向力和力矩载荷的联合作用下，球轴承滚珠和保持架呈现6个方向的自由度，而内圈具有5个自由度，包括内圈质心在径向YZ平面内平动以及绕X轴转动的3个时变自由度和绕Y轴、Z轴倾斜的2个固定自由度。外圈可绕轴线发生转动[11]。

角位置为ψj处的钢球j(j=1,2…Z)，其刚度sjs和阻尼cjs与接触载荷Q有关，该处的刚度矩阵和阻尼矩阵可用虚功原理求得。其总刚度矩阵和总阻尼矩阵表示为：

(7)

(8)

式中，α为角接触球轴承的初始接触角。

1.2 滚动轴承钢球-滚道接触副的相互作用力

在球轴承钢球-滚道接触副的Hertz接触区内任一点P(x0,y0)相对于球几何中心的位置向量可表示为：

(9)

其中，R′为考虑磨损后接触椭圆曲率半径。

接触坐标系中，在P点处套圈和球的速度分别为：

(10)

(11)

其中，

Rp=rp+rb-rr

(12)

套圈在P点相对于球的局部滑动速度为：

(13)

本文考虑油膜阻尼对球与套圈之间摩擦作用力的影响，油膜阻尼为：

Λc8exp(-Λc9)γc10

(14)

考虑到滞后阻尼会影响球与套圈之间的摩擦作用力，引入粘滞阻尼系数为：

(15)

式中，αe是与恢复系数相关的系数，对于碳钢材料，αe=0.08～0.32s/m。

球在接触点处受到的法向作用力为：

(16)

等效摩擦系数的表示为：

μ=μbdqbd+μhd(1-qbd)

(17)

其中，μhd为摩擦拖动系数，μbd为边界润滑时的拖动系数，qbd为粗糙表面微凸体所承受的负荷比例。

因而，接触椭圆的摩擦拖动力为：

Tbr=μ|Fbrn|

(18)

则摩擦拖动力在接触椭圆长半轴和短半轴方向上的分量为：

Tbrx=-Tbrsinθ

(19)

Tbry=Tbrcosθ

(20)

因此，在接触坐标系中，球受到的摩擦非线性激励矩阵为：

(21)

在惯性坐标系中，滚道受到球产生的作用力向量为：

(22)

1.3 滚动轴承的动力学建模及计算流程

如式(1)所示，有了球轴承的质量矩阵，刚度矩阵、阻尼矩阵和载荷矩阵可建立球轴承的振动微分方程。

结合式(7)、式(8)和式(22)，可得到球轴承的振动微分方程：

(23)

首先确定轴承零件的几何结构参数和运动条件初始值，通过静力学的方法得到轴承各个零件的运动速度和最小油膜厚度，用牛顿-拉夫逊法求解轴承受力平衡方程，得到所有位置钢球的工作接触角和接触载荷，从而利用雷诺方程计算出轴承的刚度矩阵和阻尼矩阵。通过钢球与滚道相对位置及运动参数的计算，获得钢球与滚道局部接触相对速度的表示，并结合之前的刚度矩阵和阻尼矩阵，确定滚动球轴承的振动微分方程。

1.4 滚动轴承固有振动特性分析

方程(23)为描述球轴承3个方向上振动的非齐次二阶线性微分方程[12]，则滚动轴承振动加速度的频谱为：

(24)

(25)

式中，fr为球轴承振动的固有频率,ξr为球轴承振动阻尼系数。通过式(24)和式(25)，可以得到滚动轴承固有振动的幅频特性图1和相频特性图2。

图1 振动加速度幅频特性

图2 振动加速度相频特性

2 滚动轴承振动机理分析

2.1 轴承零件损伤振动机理分析

轴承零件表面存在损伤缺陷，轴承在运转过程中经过损伤点会产生脉冲激振力[13]。

若外圈存在单个损伤点，激振力为：

(26)

若内圈存在单个损伤点，激振力为：

(27)

若滚动体存在单个损伤点，激振力为：

(28)

上式中To、Ti、Tb为轴承元件缺陷周期，由元件缺陷频率可求出。

2.2 损伤缺陷激励下球轴承的振动求解

依据方程(23)描述的系统响应函数为：

(29)

该函数的模和相位差就是式(24)、式(25)的幅频特性和相频特性。损伤缺陷激振力F(t)进行Fourier变换得到F(ω)，与轴承系统的频率响应函数H(ω)相乘得到X(ω)，再进行Fourier反变换得到球轴承振动响应x(t)，即为损伤缺陷激励引起的轴承振动。损伤缺陷激励F(t)引起的球轴承振动响应求解步骤如图3所示。

图3 损伤缺陷激励下球轴承振动的求解步骤

3 轴承振动实验结果分析

通过准确建立轴承振动信号测试系统，实时采集轴承原始数据并对其进行分析和处理，从本质上研究轴承振动特性。对型号为LCY6211深沟球滚动轴承进行试验，通过对采集到的振动信号分析对本文所建模型进行验证。滚动轴承振动测试试验台如图4所示。

图4 轴承振动测试试验台

在本次试验过程中，电机转速为2000r/min，径向施加载荷10kN，采样频率设置为20kHz，通过轴承振动测量试验可得轴承正常和局部损伤的时域振动信号如图5所示。

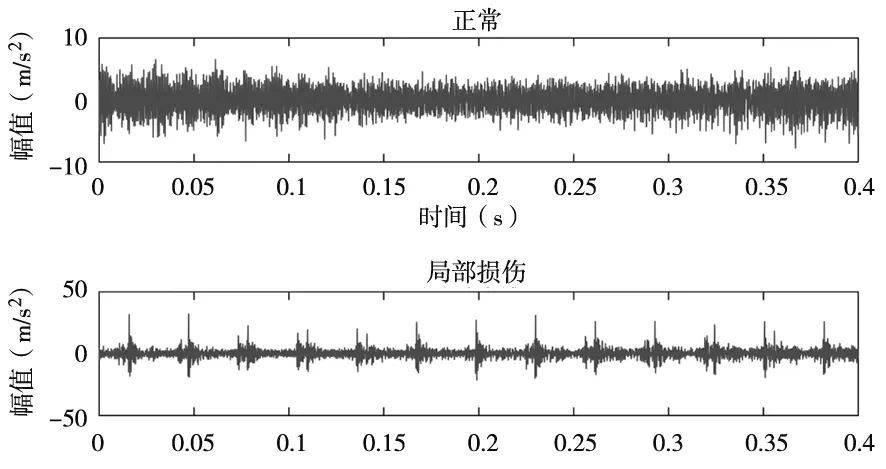
图5 轴承振动时域信号

图5中对比滚动轴承正常和局部损伤的振动时域信号，发现轴承运行在经过局部损伤处，时域的幅值明显提高。

图6 轴承正常频域图

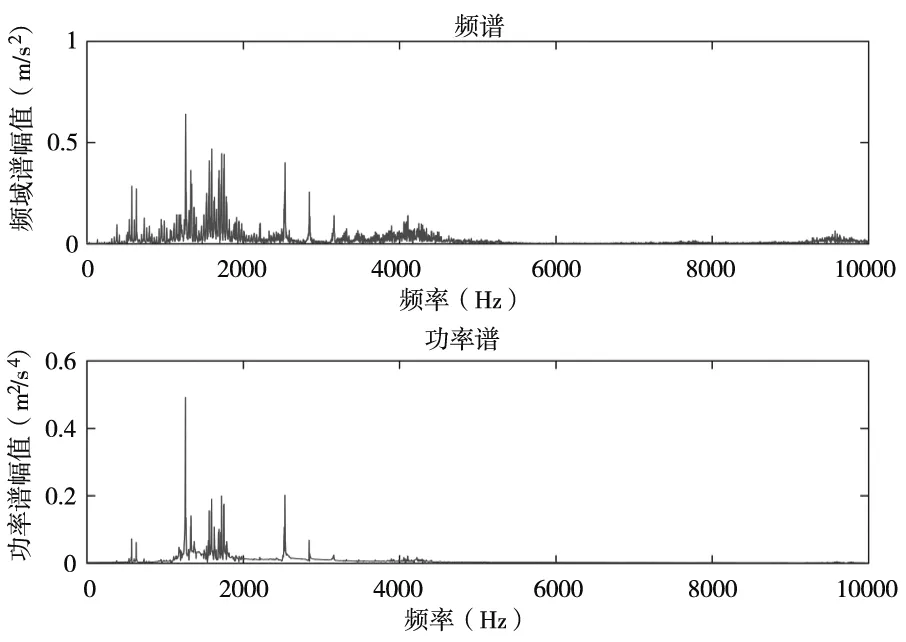
图7 轴承局部损伤频域图

通过傅里叶变换将轴承正常和局部损伤的时域信号转换得到频域信号，对比图6和图7的频谱易得出轴承出现了局部损伤，但是对于轴承损伤出现在轴承元件位置处无法清晰判断，因此对出现原始信号进行小波包络分析，得到轴承正常和局部损伤引起振动的包络图，如图8和图9所示。

图8 轴承正常运行包络图

图9 轴承内圈损伤缺陷包络图

对比图8和图9，得到轴承运转过程中经过损伤缺陷处，会产生激振力引起轴承振动。通过试验采集到的振动信号产生的激振频率为190.7Hz、381.0Hz、571.5Hz，与内圈局部损伤缺陷特征频率fi=190.4Hz基本一致或为其倍频。

4 结论

本文在滚动轴承理论研究的基础上，建立了滚动轴承动力学模型，并通过仿真和实验得出以下结论：①对振动微分方程求解得出轴承的固有振动属性，为滚动轴承的设计提供了参考；②当轴承产生局部损伤缺陷时，振动信号在时域的幅值明显会增大，同时在频域也会发生较大的变化；③对实验中采集到的滚动轴承振动信号进行小波包络分析，观察到激振频率与内圈的局部损伤缺陷特征频率一致或为倍频，可以判断出损伤缺陷出现在轴承内圈位置处。后续将考虑波纹度、损伤缺陷程度、载荷等因素，结合动力学模型分析它们对轴承振动产生的影响。