城市轨道交通列车节能操纵策略研究

曹佳峰

（中铁第五勘察设计院集团有限公司线路运输设计处，北京102600)

0 引言

城市轨道交通列车具有安全、正点、环保等特点,随着运营里程和开行对数的增加,城市轨道交通系统的能耗迅速增长。通过数据统计,城市轨道交通系统总能耗的50%以上均与列车运行能耗相关。在确保列车安全正点运行的前提下,如何通过合理的操纵策略降低运行能耗,成为城市轨道交通列车节能优化领域的研究热点。

国内外专家对城市轨道交通列车节能操纵策略展开深入研究。Milroy[1]在分析列车节能操纵理论的基础上,提出了四阶段操纵策略,即“牵引—匀速—惰行—制动”。Howlett[2]采用极大值原理证明了列车在平缓坡道运行时节能操纵策略包含加速、匀速、惰行、制动4种工况,并且对工况转换点进行算法求解。李晋[3]提出以单列车节能为主、多列车节能为辅的列车能耗监测及节能方案。余进等[4]建立列车多目标优化模型,引入多目标微粒群算法获得不同操纵控制策略,使得列车在运行能耗、运行时间和精确停车之间得到很好的折衷效果。王青元等[5]提出了满足限速条件下列车最优切换规则,求解最优工况速度及最优切换时机。厉高等[6]建立列车在定时约束下的节能最优控制模型,通过实例仿真验证了该模型的节能效果。黄舰等[7]提出了基于惰行控制的操纵策略,设计了快速搜索惰行点的优化算法。

目前,既有研究成果主要集中在四阶段操纵策略和惰行控制策略下的能耗建模、算法求解和实例仿真,较少研究不同线路条件下典型操纵策略对列车能耗的影响。因此,以城市轨道交通列车牵引计算为基础,针对典型的四阶段操纵策略和惰行控制操纵策略,分别构建单列车区间定时节能操纵能耗模型,选取5种不同坡道类型,通过案例设计分析2种操纵策略下列车牵引能耗、再生制动储能和总能耗的差异,经过仿真得到相应的速度距离曲线。

1 城市轨道交通列车节能操纵模型

以城市轨道交通列车动力学模型为基础,分别构建四阶段操纵策略能耗模型和惰行控制操纵策略能耗模型,采用粒子群算法(Particle Swarm Optimization,PSO)求解模型,为不同坡道下的案例设计与仿真分析提供理论依据。

1.1 城市轨道交通列车动力学模型

以城市轨道交通列车牵引计算为基础,可知列车在运行过程中主要受到牵引力、基本阻力、附加阻力和制动力的综合作用[8]。根据《列车牵引计算规程》[9]中相关规定,将列车简化为单一质点。列车所受合力取决列车不同运行工况,可表示为

式中：C为列车所受合力,N；F为牵引力,N；W0为基本阻力,N；Wj为附加阻力,N；B为制动力,N；w0(v)为单位基本阻力,N/kN,w0(v) =av2+bv+c,其中a,b,c为阻力常数,根据固定车型确定,v为列车速度,km/h；g为重力加速度,g = 9.8 m/s2；Wi为坡道附加阻力其中i为坡道坡度,‰；Wr为曲线附加阻力其中R为曲线半径,m。

在对列车进行受力分析及确定合力的基础上,建立城市轨道交通列车动力学模型为

1.2 四阶段操纵策略能耗模型

1.2.1 操纵原理

目前城市轨道交通列车采用无级牵引的模式,该模式下列车牵引力和制动力均根据特性曲线取值。四阶段操纵策略原理为：列车首先以最大牵引力加速到速度v1,然后以速度v1匀速运行t2时间,接着切换至惰行工况直到速度降至v2,最后制动进站停车。在此过程中,列车运行速度v始终小于线路限速vlim。四阶段操纵策略示意图如图1所示。

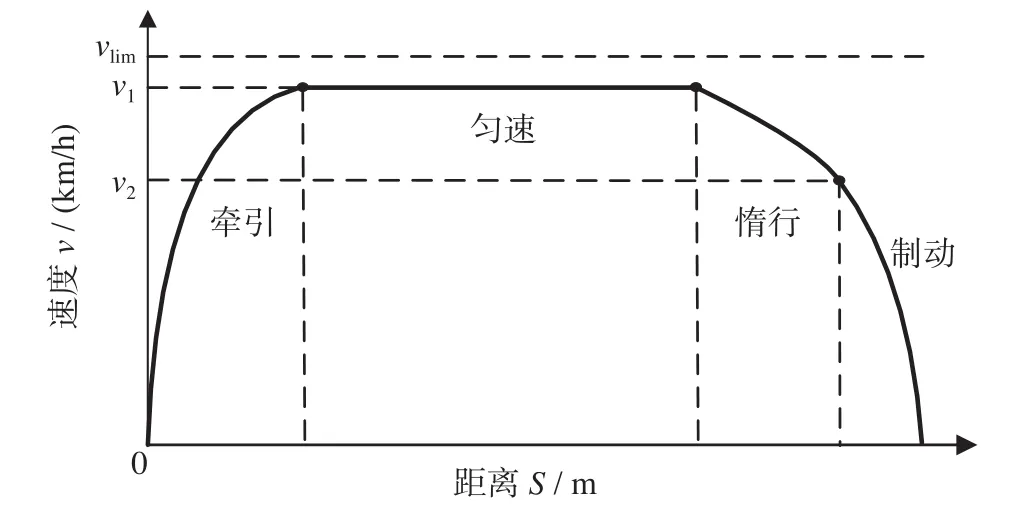
图1 四阶段操纵策略示意图Fig.1 Four-stage manipulation strategy

由图1可知,在满足列车站间运行约束条件下,四阶段操纵策略中列车不同工况之间的切换是通过v1,t2,v2连接起来,以此得到最优的速度距离曲线。

1.2.2 模型建立

（1）牵引工况下,列车从初速度0加速到v1,则运行时间、运行距离和能耗可分别表示为

式中：t1为牵引工况下运行时间,s；s1为运行距离,m；E1为牵引工况能耗,kW·h。

（2）匀速工况下,列车以速度v1匀速运行t2时间,则运行距离和能耗可分别表示为

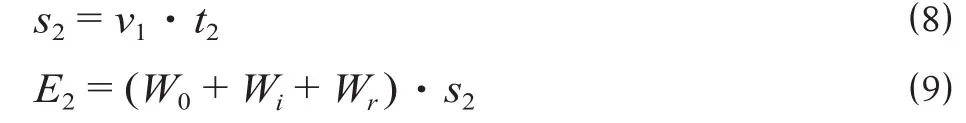
式中：s2为匀速工况下运行距离,m；E2为匀速工况能耗,kW·h。

（3）惰行工况下,列车由速度v1惰行减速至v2,惰行工况下不产生耗能,即E3= 0,则运行时间、运行距离可分别表示为

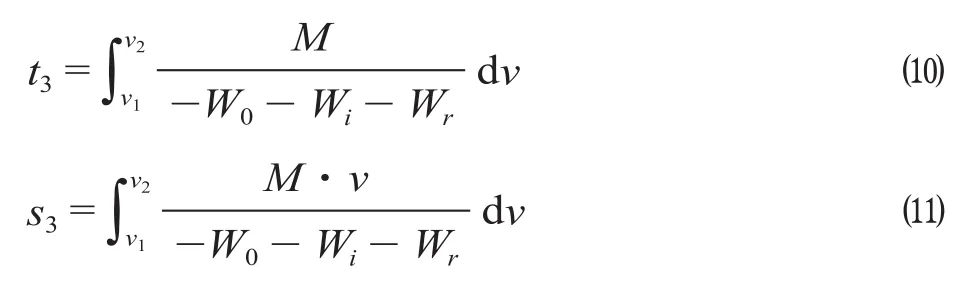
式中：t3为惰性工况下运行时间,s；s3为运行距离,m。

（4）制动工况下,车载再生设备把列车的动能转换为电能反馈到接触网,降低总能耗。假设列车以恒定减速度进站停车,则恒定减速度、运行时间和再生制动产生的能量可分别表示为

式中：ab为恒定减速度,m/s2；S为站间距离,m；t4为制动时间,s；E4为再生制动能量,kW·h。

四阶段操纵策略下,列车牵引能耗Eq=E1+E2,再生制动储能Ez=E4。若再生制动储能利用率以50%计算,且列车满足安全正点、精确停车等各项约束条件,以此建立的能耗模型为

式中：E为总能耗,kW·h；η为牵引电机效率,一般取85%；T为实际运行时间,s；t为正点运行时间,s；v(x0)和v(xs)为列车起点和终点的运行速度,km/h；v(xi)为列车在xi处的瞬时速度,km/h；vlim为线路限速,km/h。

1.2.3 模型求解

列车节能操纵是一个复杂的非线性规划问题,模型中涉及的运行时间、运行距离、能耗均可以通过动力学方程积分求解。PSO算法作为一种进化算法,具有收敛快、精度高等优点,能在有限迭代次数下找到逼近最优解的满意解,在此类问题中广泛应用。采用PSO算法求解城市轨道交通列车四阶段操纵策略能耗模型,将求解过程转化为约束条件下目标函数的寻优过程,步骤如下。

（1）实数编码。将能耗模型中最高速度v1、匀速运行时间t2、惰行后速度v2等参数进行实数编码,并将参数的搜索范围都限制在条件约束范围内。

（2）初始化粒子群。以v1,t2,v2等参数作为搜索粒子,初始化其数值。

（3）对于种群内每个粒子,根据公式 ⑸ 至公式⒆计算其适应度值。

（4）将其适应度值与经过的个体最优解作比较,如果较好,将其作为当前个体最优解。

（5）将其适应度值与经过的全局最优解作比较,如果较好,将其作为当前全局最优解。

（6）更新个体最优解和全局最优解。

（7）迭代次数加1,当达到最大迭代次数时,转入步骤（8）；否则转入步骤（3）。

（8）输出粒子最优解,将其代入能耗模型中得到最低能耗值。

1.3 惰行控制操纵策略

1.3.1 操纵原理

惰行控制操纵策略原理为：在列车站间运行过程中,插入n个“牵引-惰行”工况转换点x1,x2,…,xn,且x0＜x1＜x2＜ … ＜xn＜xs。在列车惰行操纵运行范围内,(x0,x1)是第1个工况运行范围,为牵引加速状态；(x1,x2)是第2个工况运行范围,为惰行减速状态；(xj-1,xj)是第j个工况运行范围,直到列车运行至xn位置时采用制动工况进站停车。

惰行操纵策略使得列车在站间运行时切换不同工况,结合线路中存在的起伏坡道和长大下坡道,充分惰行且避免站间发生不必要的制动,达到降低牵引能耗的效果。惰行操纵策略示意图如图2所示。

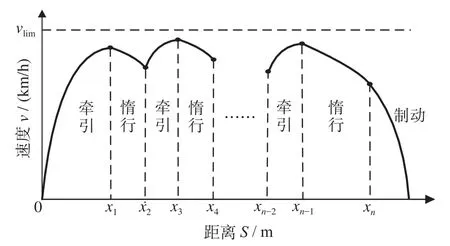
图2 惰行操纵策略示意图Fig.2 Coasting control manipulation strategy

1.3.2 模型建立

（1）当(xj-1,xj)内为牵引工况时,列车的运行时间、运行距离、能耗可分别表示为

式中：tj为牵引工况下运行时间,s；sj为运行距离,m；Ej为牵引能耗,kW·h。

（2）当(xj-1,xj)内为惰行工况时,Ej= 0,列车的运行时间、运行距离可分别表示为

式中：tj为惰性工况下运行时间,s；sj为运行距离,m。

（3）当(xn,xs)内为制动工况时,采用反向迭代法确定制动点位置xn。假设列车制动时速度为vb,制动距离为sb,则制动工况的运行时间、再生制动产生的能量可分别表示为

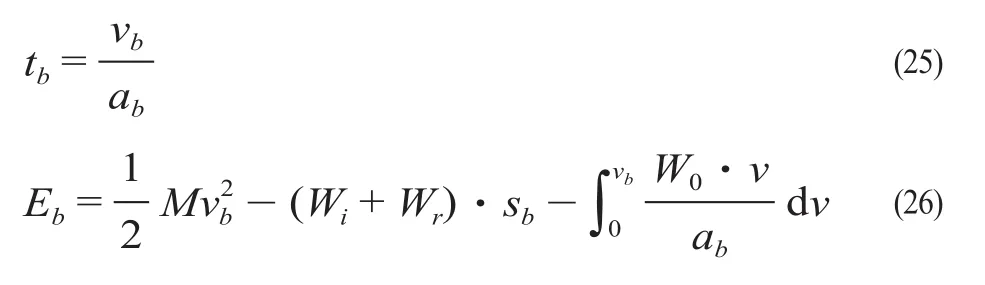
1.3.3 模型求解

再次使用PSO算法求解城市轨道交通列车惰行控制操纵策略能耗模型,不同之处在于：将“牵引-惰行”工况转换点x1,x2,…,xn等参数进行实数编码,将上述参数作为搜索粒子,初始化其数值。针对每一个搜索粒子,根据公式⒁至公式⒄ 计算其适应度值,不断更新个体最优解和全局最优解,具体步骤如下。

（1）将其适应度值与经过的个体最优解作比较,如果较好,将其作为当前个体最优解。

（2）将其适应度值与经过的全局最优解作比较,如果较好,将其作为当前全局最优解。

（3）更新个体最优解和全局最优解,迭代次数加1；当达到最大迭代次数时,输出粒子最优解,将最优解代入能耗模型中得到最低能耗值。

2 案例设计与仿真分析

选用4动2托的A型列车为研究对象,A型列车基本参数如表1所示。针对平坡道、长区间起伏坡道、短区间起伏坡道、长大上坡道、长大下坡道5种不同坡道,采用PSO算法(其中设置粒子群规模为20,迭代次数为100次,学习因子为2,超时惩罚因子和超速惩罚因子为1),求解四阶段操纵策略能耗模型和惰行控制操纵策略能耗模型,分析2种策略能耗模型下列车牵引能耗、再生制动储能和总能耗的差异,并仿真得到相应的速度距离曲线。

表1 A型列车基本参数Tab.1 Basic parameters of type A train

（1）平坡道。站间线路全长3 000 m,正点运行时间为168 s,限速均为80 km/h,仿真得到2种操纵策略下的平坡道速度距离曲线如图3所示。

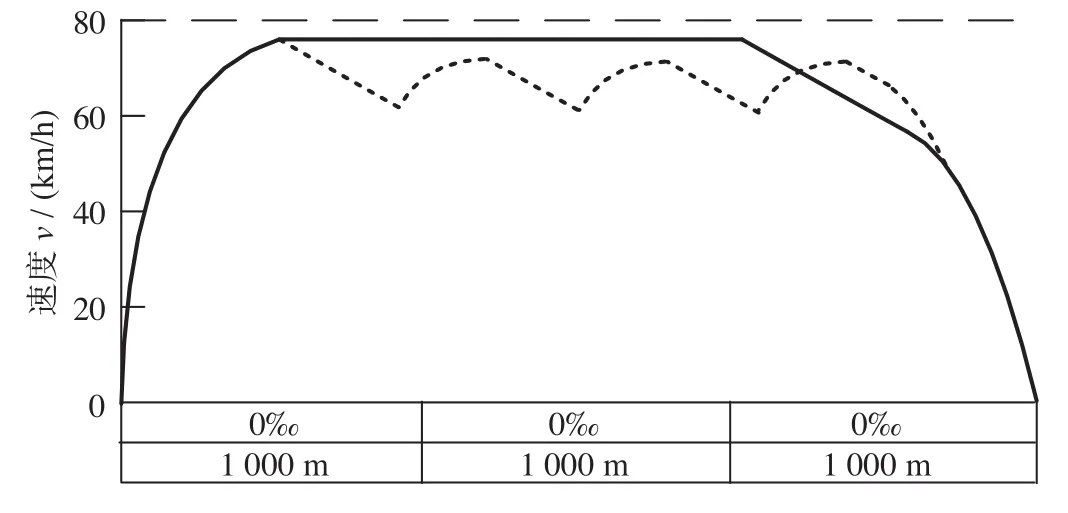
图3 2种操纵策略下的平坡道速度距离曲线Fig.3 Speed distance curve of flat ramp under two control strategies

（2）长区间起伏坡道。站间线路全长4 000 m,正点运行时间为240 s,仿真得到2种操纵策略下长区间起伏坡道速度距离曲线如图4所示。当站间存在起伏坡道时,惰行控制操纵策略下列车充分利用下坡重力势能,尽可能采用惰行工况以减少牵引能耗。

图4 2种操纵策略下长区间起伏坡道速度距离曲线Fig.4 Speed distance curve of long interval undulating ramp under two control strategies

（3）短区间起伏坡道。站间线路全长2 000 m,正点运行时间为135 s,仿真得到2种操纵策略下短区间起伏坡道速度距离曲线如图5所示。

图5 2种操纵策略下短区间起伏坡道速度距离曲线Fig.5 Speed distance curve of short interval undulating ramp under two control strategies

（4）长大上坡道。线路全长3 000 m,正点运行时间为185 s,仿真得到2种操纵策略下长大上坡道速度距离曲线如图6所示。当站间存在长大上坡道时,四阶段操纵策略下列车保持较低匀速速度通过坡道；惰行控制策略下列车在平坡时尽可能加速,在坡度值较大的坡道尽量采用惰行工况,减少坡道附加阻力所做负功。

图6 2种操纵策略下长大上坡道速度距离曲线Fig.6 Speed distance curve of long uphill ramp under two control strategies

（5）长大下坡道。线路全长3 200 m,正点运行时间为195 s,仿真得到2种操纵策略下长大下坡道速度距离曲线如图7所示。

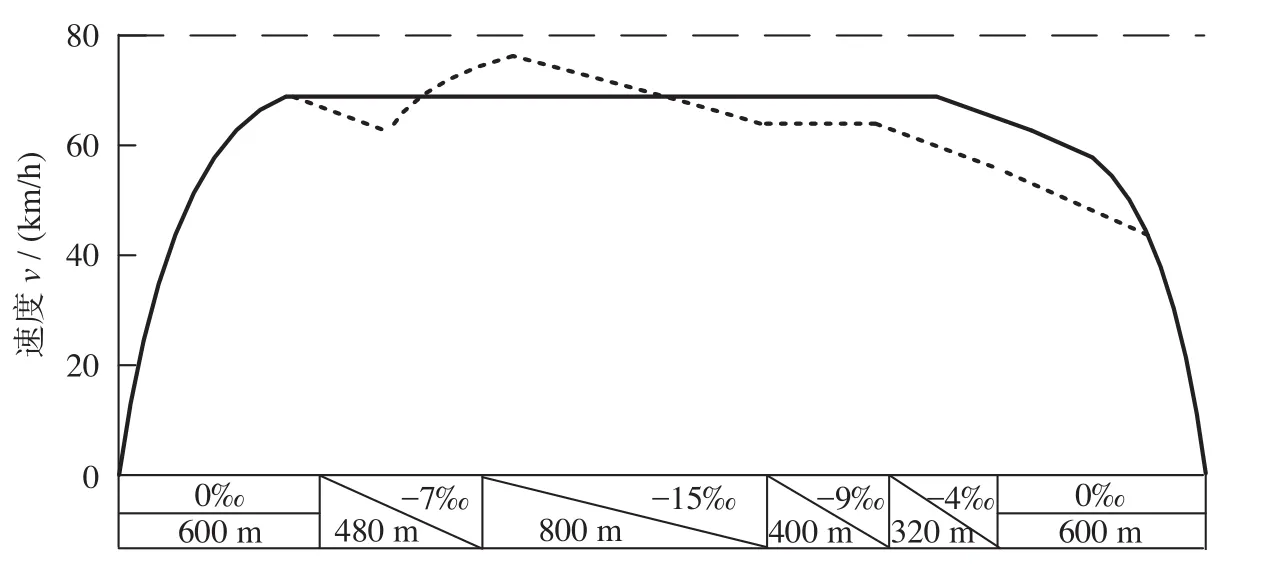
图7 2种操纵策略下长大下坡道速度距离曲线Fig.7 Speed distance curve of long downhill ramp under two control strategies

上述5个案例中,四阶段操纵策略能耗计算结果如表2所示,惰行控制操纵策略能耗计算结果如表3所示。

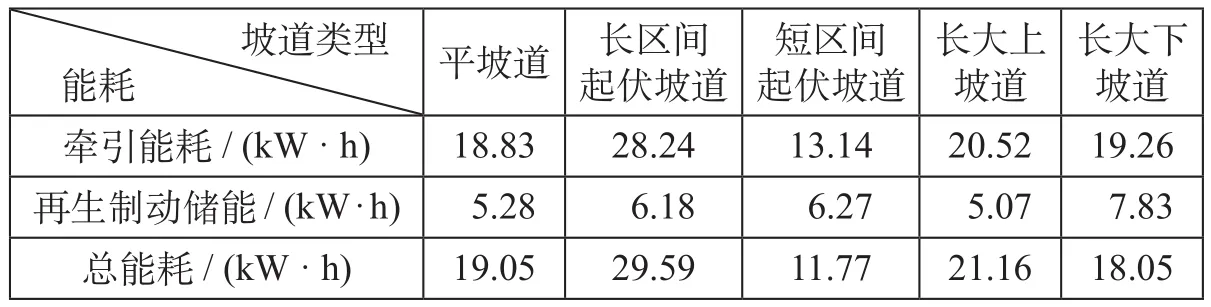
表2 四阶段操纵策略能耗计算结果Tab.2 Calculation result of four-stage manipulation strategy

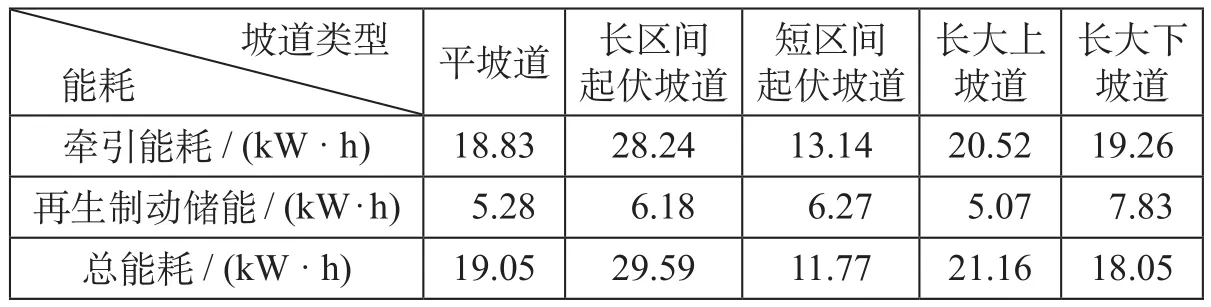
表3 惰行控制操纵策略能耗计算结果Tab.3 Calculation result of coasting control manipulation strategy

通过案例设计和模拟仿真,结合表2和表3计算数据,得出以下结论。

（1）四阶段操纵策略在牵引能耗方面,除长大下坡道,均优于惰行控制操纵策略,这和列车在站间运行时速度波动越小牵引能耗越低的理论研究相吻合。

（2）惰行控制操纵策略在再生制动储能方面略优于四阶段操纵策略,且坡道变化越平缓,列车就无法利用线路条件充分惰行,导致其在较高运行速度就转为制动工况,停车进站。因此,列车在平坡道运行时产生的再生制动储能最高。

（3）总能耗方面,平坡道和长区间起伏坡道中四阶段操纵策略的牵引能耗较惰行控制操纵策略的牵引能耗分别下降10%左右,长大下坡道中惰行控制操纵策略的牵引能耗较四阶段操纵策略的牵引能耗下降10%左右,短区间起伏坡道和长大上坡道的总能耗相近。

综上所述,四阶段操纵策略总体上优于惰行控制操纵策略,但是考虑到惰行操纵策略灵活性强且节能潜力更大,应结合实际线路情况,协同使用2种策略,达到节能优化效果。

3 结束语

随着城市轨道交通系统运营里程和开行对数的增加,列车运行能耗迅速增长,而且约占城市轨道交通系统总能耗的50%以上。城市轨道交通列车节能操纵策略研究,通过设计5种不同线路坡道仿真得到2种操纵策略对城市轨道交通列车牵引能耗、再生制动储能和总能耗的影响,力求在确保列车安全正点运行的前提下,通过合理的列车操纵策略降低运行能耗,而且研究结果对列车选择适合的节能操纵策略具有一定借鉴意义。另外,还应以多质点能耗模型为基础,细化列车受力情况,提升建模精度,通过实例仿真增强城市轨道交通列车节能操纵策略的实用性。